基于RBF神经网络的模拟电路智能故障诊断

乔维德

（无锡开放大学 科研与质量控制处，江苏 无锡 214011）

0 引 言

由于电子技术的迅速发展，现代电子设备的集成化程度越来越高，也带动了集成电路的快速发展。数模混合电路属于集成电路的重要组成部分，数模混合电路中出现的故障直接影响集成电路的正常运行，所以广大科技工作者及学者更关注数模混合电路的故障问题。据统计，集成电路器件或设备中，数字电路占数模混合电路的八成左右，数字电路因为数字电子器件自身的稳定性，一般不易发生故障，但集成电路器件或设备中80%的故障来自模拟电路部分。针对模拟电路故障诊断，学者提出了相应的技术方案，如利用节点电压灵敏度比值法、基于改进马氏距离等传统故障诊断方法。许多学者一直关注人工智能技术在模拟电路故障诊断中的研究，先后提出将BP神经网络、小波神经网络、径向基函数（RBF）神经网络用于故障诊断的方法，并利用粒子群算法、遗传算法、果蝇算法、蚁群算法、狼群算法优化模拟电路故障诊断的神经网络模型[1-6]。以上方法在模拟电路故障的实际诊断中都取得了一定效果，但仍存在明显缺陷。BP算法、遗传算法在优化训练过程中收敛速度慢，计算量大，易陷入局部极小；粒子群算法易出现“早熟”，且在没有完全搜索前易陷入局部极值；果蝇算法前期搜索能力强、收敛速度快，但后期局部搜索能力弱；蚁群算法寻优时搜索时间较长、过程较慢，易产生停滞现象；狼群算法全局收敛速度快，但极易陷入局部极值；小波分析只是分解故障信号低频部分，却忽略故障信号中高频部分，导致高频分量中有用信息丢失，易造成模拟电路故障的误诊断。现有故障诊断中主要针对电路元件的单软故障较多，而对电路多软故障涉及较少。本文利用小波包分析提取模拟电路的故障特征能量谱信号，建立基于果蝇-粒子群算法优化的RBF神经网络模型，以期实现模拟电路的智能故障诊断。

1 模拟电路智能故障诊断模型

模拟电路智能故障诊断模型原理如图1所示。其诊断过程主要包括模拟电路故障数据采集、故障信号特征向量提取、RBF神经网络故障诊断。E30～E37表示从模拟电路检测采集的原始故障数据进行小波包变换（WPT）后的故障特征向量值，基于RBF神经网络的模拟电路故障诊断模型，首次设计一种果蝇-粒子群算法用来对RBF神经网络加以优化。E30～E37作为RBF神经网络的输入量，S1,S2,S3,S4作为RBF神经网络的实际输出量，可根据它们的不同状态组合诊断模拟电路的正常运行及p种故障状态Y0～Yp。

图1 模拟电路智能故障诊断模型原理

2 模拟电路故障特征提取

利用WPT对模拟电路故障信号在低频、高频等不同频带部分进行精确分解，计算不同频带段上的频带能量，作为模拟电路故障特征。本文选取WPT的分解层数为3，其小波包分解原理如图2所示[7]。

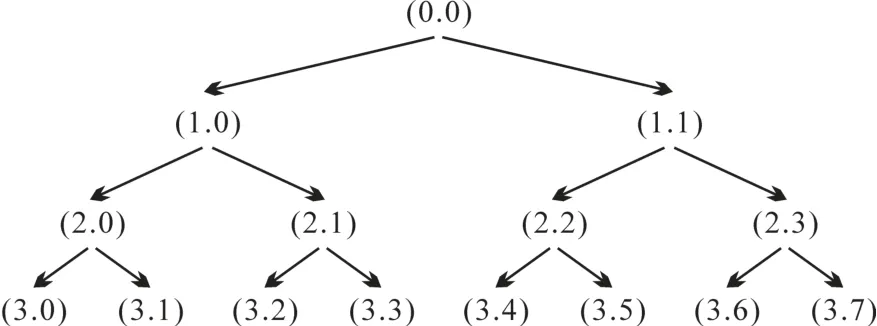
图2 小波包分解原理

将各频段的信号能量进行归一化处理后得到的模拟电路故障特征向量为[8]：

3 RBF神经网络优化

RBF神经网络结构模型如图3所示。

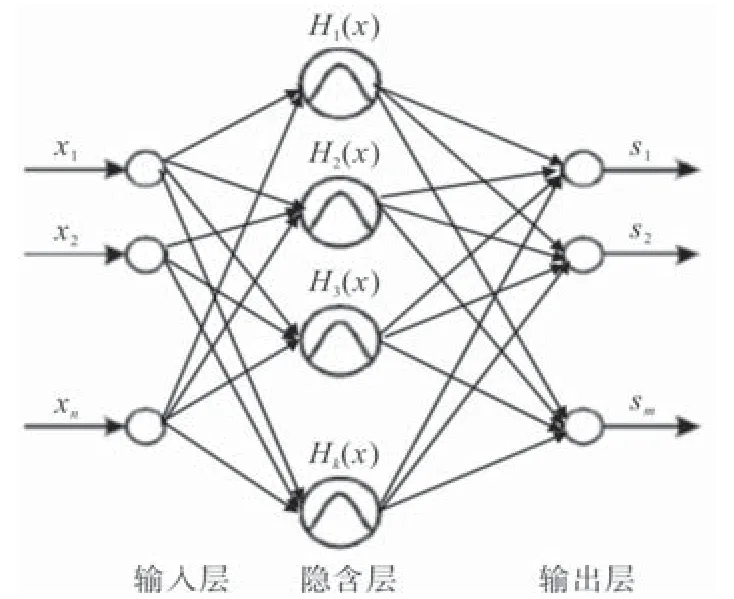
图3 RBF神经网络结构模型

RBF神经网络结构中隐含层单元采取径向基高斯函数Hi，x1～xn为RBF神经网络输入量，s1～sm为RBF神经网络输出量，RBF神经网络的第d个输出表示为：

其中，ωid为隐含层与输出层之间的连接权值，Hi为第i个径向基高斯函数，即：

其中，ci为径向基高斯函数的中心，δi为径向基高斯函数的宽度，i=1, 2, …,k（k为RBF神经网络隐含层神经元节点数）。采取上述RBF神经网络对模拟电路故障加以诊断时，由于ci,δi,ωid等结构参数直接影响RBF神经网络的运行速度及其诊断精度[9]，因而采用果蝇-粒子群算法对RBF神经网络结构进行优化。果蝇算法在前期运行中全局搜索能力强、收敛速度快，能使果蝇迅速搜索出全局较优值区域，但后期局部搜寻时速度变慢、寻优精度不高；粒子群算法优势是搜索速度快、寻优精度高。因此，将果蝇算法与粒子群算法进行融合形成果蝇-粒子群算法，可整体提高其运行速度和优化精度。运用果蝇-粒子群算法优化RBF神经网络结构参数的步骤如下[10]：

（1）初始化算法参数。设果蝇算法中的果蝇群体数量为M，果蝇算法最大迭代次数为num1，果蝇群体初始随机位置为（X0,Y0），果蝇优化迭代步进值为v；粒子群算法中的最大迭代次数num2，最大和最小惯性权重为ωmax,ωmin。

（2）确定果蝇个体位置坐标。果蝇个体通过嗅觉按下列规则搜寻食物目标的方向及其距离，即：

（3）求果蝇个体的味道浓度。设hi为果蝇位置与原点之间的距离，Gi为果蝇个体的味道浓度判定值，Fit为味道浓度判别函数（适应度函数），Concentration为果蝇个体位置对应的味道浓度，则

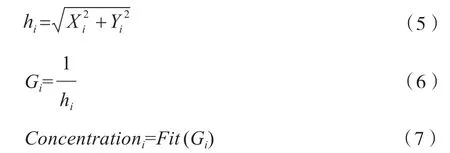
（4）搜寻全局最高味道浓度的果蝇个体，则

从果蝇群体中搜寻味道浓度最高的果蝇个体，其味道浓度值为bestConcentration，位置坐标值对应X,Y，同时其他果蝇个体通过敏锐的嗅觉飞向靠近该坐标值位置，从而生成新的果蝇群聚位置，即：

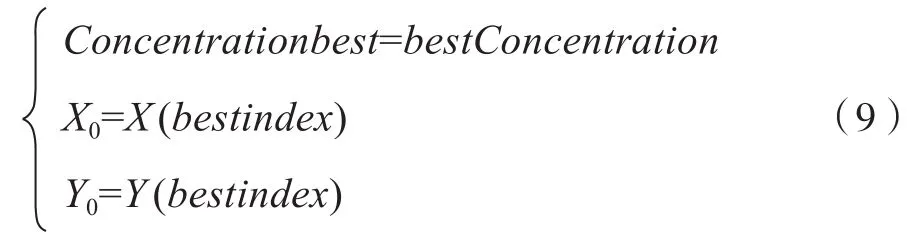
（5）果蝇迭代寻优。当果蝇算法的迭代次数没有满足最大迭代次数num1时，转入第2步重复执行，否则转入第6步执行。

（6）将通过果蝇算法寻优并组成的新果蝇群中各个体作为粒子群算法的初始种群，对种群中的粒子在d维搜索空间进行速度和位置的更新，即：

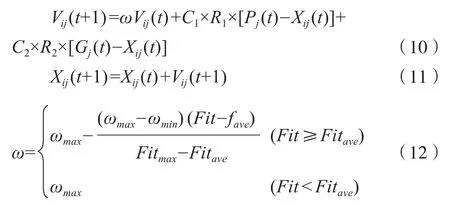
其中，j=1, 2, …,d，t为迭代进化次数；X(t)为

ij粒子在t代时的当前位置；Vij(t)为粒子在t代时的运行速度；Pj(t)为粒子最优位置，Gj(t)为种群中全部粒子最优位置；C1=C2=1.8，R1,R2取值范围为[0, 1]；Fit为粒子适应度值，Fitave,Fitmax分别为粒子平均适应度值和最大适应度值。

（7）粒子迭代寻优。当粒子群粒子进化迭代次数没有满足最大迭代次数num2时，转至第6步继续对粒子进行速度和位置的更新操作；否则输出全局最优解（位置），对应RBF神经网络的最优结构参数。

果蝇-粒子群算法优化RBF神经网络结构参数的流程如图4所示。

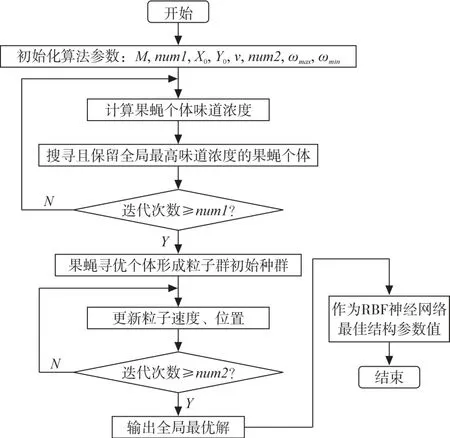
图4 果蝇-粒子群算法优化RBF神经网络结构参数的流程

将上述通过果蝇-粒子群算法优化输出的最优解个体作为RBF神经网络的最佳结构参数值，经过对学习样本的反复训练，最终得到最小均方误差。这里定义果蝇-粒子群算法的适应度为均方误差J的倒数，即Fit=1/J，则

其中，qjk为第i个训练样本在第k个输出节点处的期望输出，Sik为第i个训练样本在第k个输出节点处的实际输出，m为RBF神经网络的输出节点个数（m=4），n为学习训练样本数量。

4 仿真实验

4.1 故障特征样本选取

以巴特沃斯低通滤波器电路（见图5）为例，从中选取其故障特征样本。滤波器电路中各元器件标称值设定如下：R1=R2=R5=R6=3.5KΩ，R3=51KΩ，R4=8.55KΩ，R7=16KΩ，R8=21KΩ，C1=C2=C4=0.25μF，C3=0.18μF，运放选择LF412，电阻容差范围为5%，电容容差范围为10%。电路的输入激励信号Vin使用幅度为1V、频率为50Hz的正弦波信号，将电路输出端out作为测试点，对输出电压信号进行1～100KHz采样。通过直流灵敏度比较分析可知，当元器件C3,C4, R7, R8出现故障时，对该低通滤波器电路输出电压波形的影响变化最为明显，因而选取故障元件C3,C4, R7, R8。将低通滤波器电路状态区分为正常运行及单软故障、多软故障等类型，电路正常运行时各元器件在允许容差范围内变化。本文仿真实验选取电路的单软故障类型有C3+50%，C3-50%，C4+50%，C4-50%，R7+50%，R7-50%，R8+50%，R8-50% 8种；多软故障类型有C3+50%且C4+50%，C3+50%且C4-50%，R7-50%且R8+50%，C3-50%且R8-50%，C4+50%且R7-50%，C4-50%且R8+50% 6种。其中，C3+50%表示C3元件故障值大于其正常标称值的50%，而其它元件均在容差范围内变化；C3-50%表示C3元件故障值小于其正常标称值的50%，而其他元件均在容差范围内变化，其余元件故障类型依此类推。

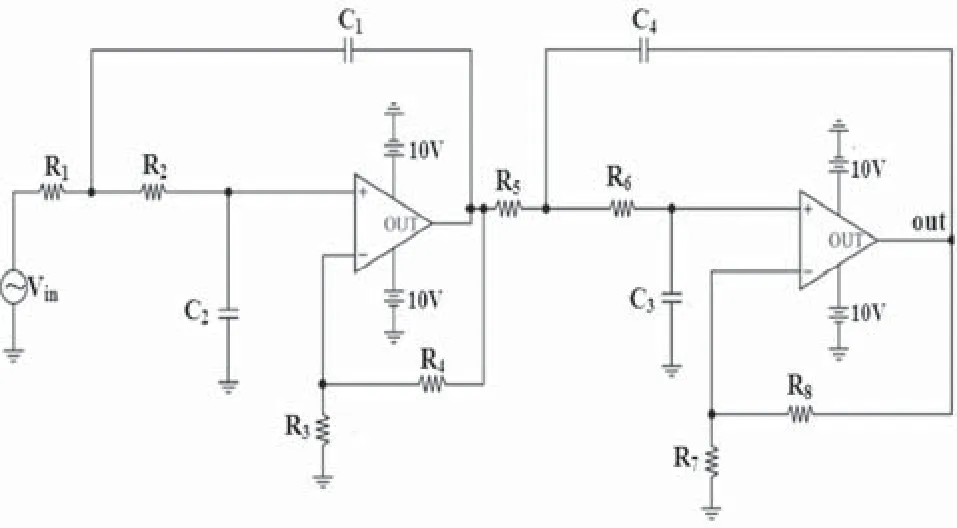
图5 巴特沃斯低通滤波器电路

以上低通滤波器电路的正常运行及单软故障、多软故障共有15种输出状态，分别对应不同二进制编码（见表1）。

采取MATLAB工具软件对巴特沃斯低通滤波器电路进行仿真分析，根据电路的正常状态和选取的14种故障状态分别做50次蒙特卡罗分析，然后，每次在电路输出out端采集不同频率时的750个特征值，每种电路状态选取40组原始数据，共600组，对每组原始数据通过WPT分解提取特征向量E30～E37作为RBF神经网络的输入量，RBF神经网络期望输出量为q1,q2,q3,q4（见表2）。其中。前500组数据作为RBF神经网络的训练样本，后100组数据作为RBF神经网络的检验样本。

4.2 参数设置与电路故障诊断分析

根据20余次实验，采用的果蝇-粒子群算法初始参数选取为：果蝇群体数量M=300，果蝇算法最大迭代次数num1=400，果蝇优化迭代步进值v=0.55；粒子群算法中最大迭代次数num2=250，惯性权重ωmax=1.6，惯性权重ωmin=0.2。RBF神经网络结构设计为8-12-4，网络搜索目标精度为0.000 1。利用表2中的训练样本训练RBF神经网络，直至RBF神经网络的输出误差达到规定的目标误差精度。RBF神经网络的检验样本诊断结果见表3。由表3可知，电路故障特征向量输入至训练完毕的RBF神经网络后，能对电路元件故障进行快速定位，且诊断准确率非常高，达到了100%。为进一步验证果蝇-粒子群算法优化RBF神经网络的寻优性能，仍采取表2中的电路故障84组样本训练数据和15组样本检验数据，分别以BP算法、遗传算法、粒子群算法、蚁群算法、果蝇算法、狼群算法对RBF神经网络进行优化训练和测试，并加以比较分析，结果见表4。由表4可知，用于低通滤波器电路故障诊断的RBF神经网络，通过果蝇-粒子群算法训练优化的电路元件故障诊断速度最快、精度最高、可靠性最好。

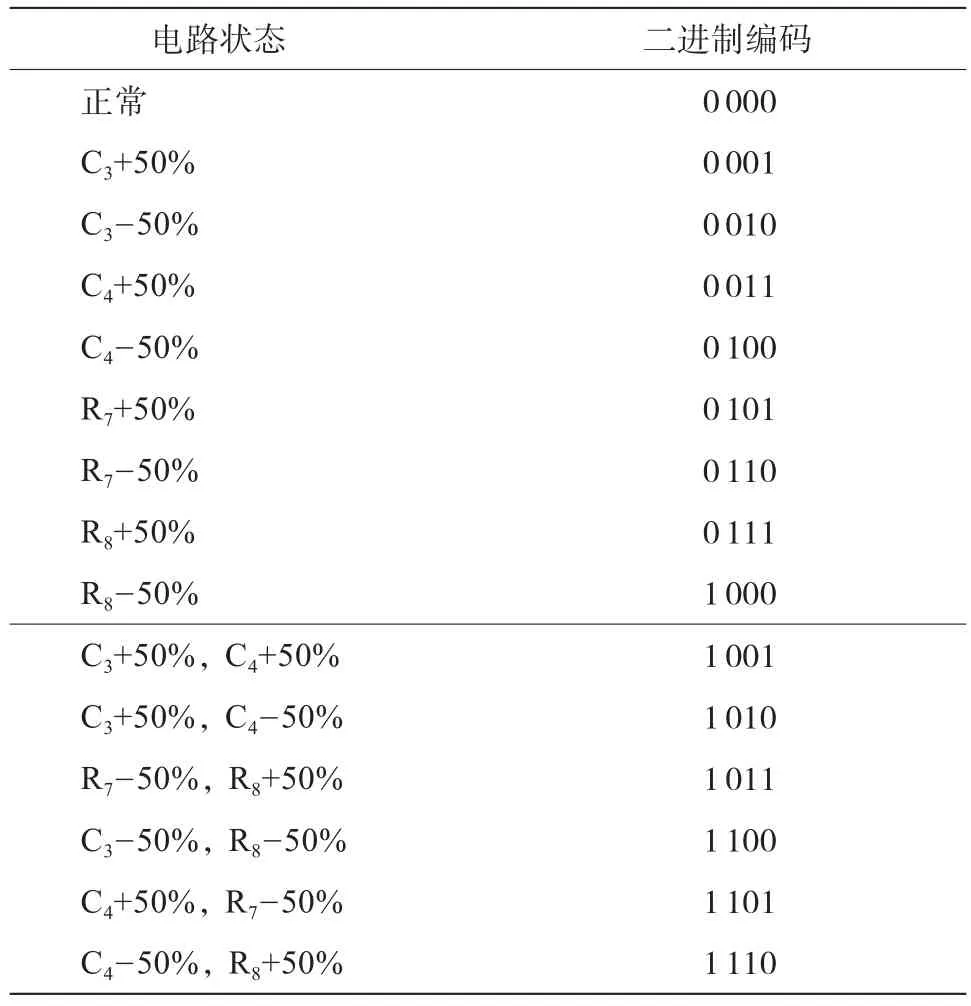
表1 电路正常及故障状态的二进制编码

5 结 语

针对巴特沃斯低通滤波器电路的故障诊断问题，提出一种基于果蝇-粒子群算法优化RBF神经网络的电路元件故障诊断模型。仿真结果表明，该诊断模型与BP算法、遗传算法、粒子群算法、蚁群算法、果蝇算法、狼群算法等智能算法优化的模拟电路神经网络模型相比，具有最快的故障诊断速度和最高的故障诊断精度。对于低通滤波器电路中的多软故障诊断，本文仅列出部分多重元件故障情况，对于元件故障电气量变化率在50%以内且对输出电压端out波形变化不明显或影响较小时，其故障诊断技术还有待深入研究。

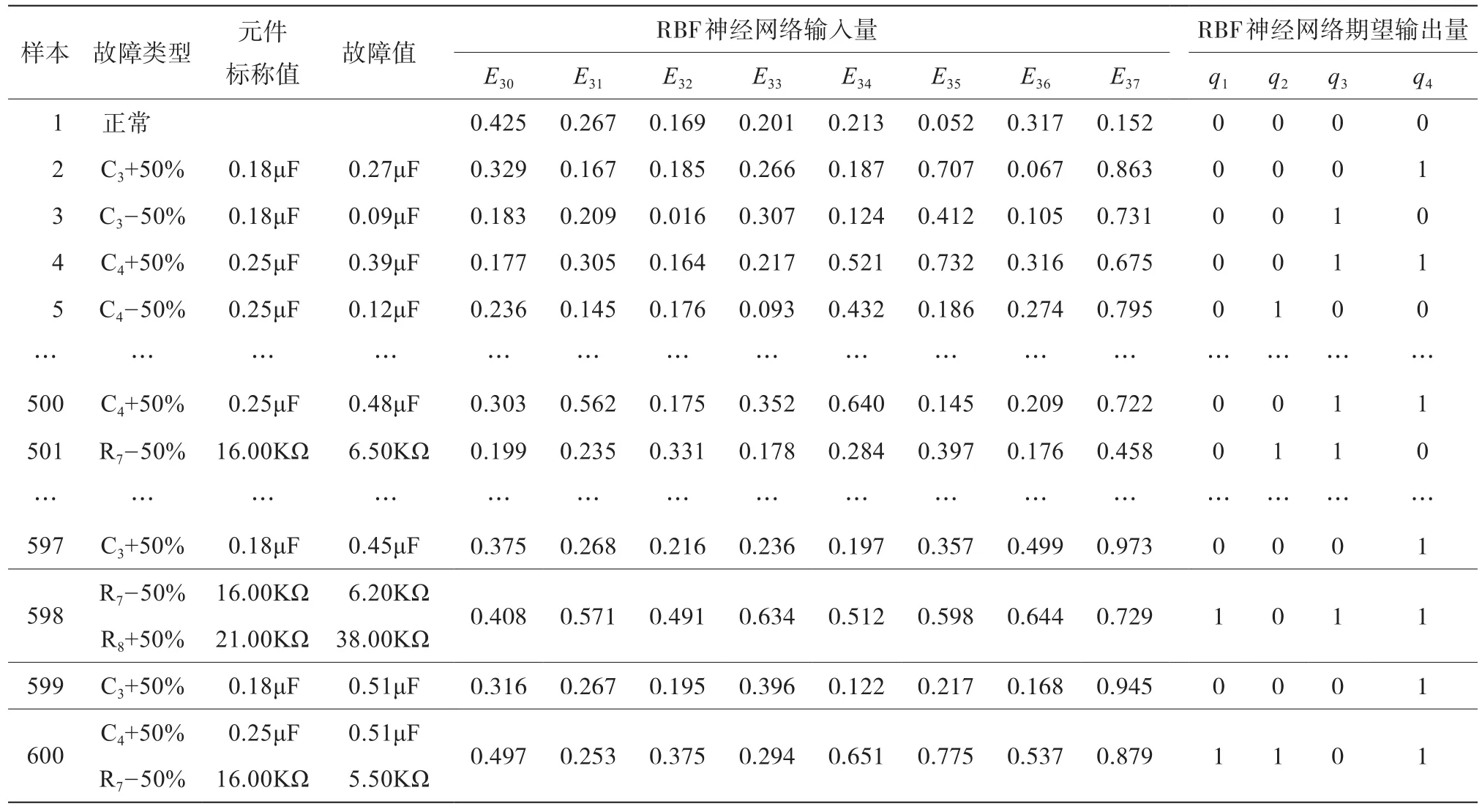
表2 RBF神经网络的训练与检验样本

表3 RBF神经网络的检验样本诊断结果

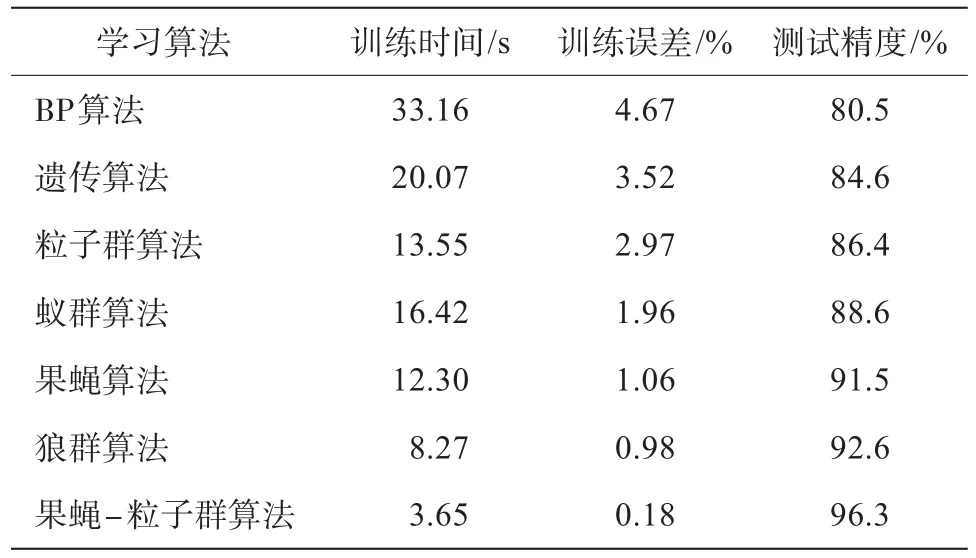
表4 RBF神经网络采取不同优化算法的比较结果

[参 考 文 献]

[1]邱世卉.小波神经网络在模拟电路故障诊断中的应用研究[J].科学技术与工程，2012，12（30）：8042-8046.

[2]李泽宇，吴文全.基于RBF神经网络的模拟电路故障诊断的研究[J].舰船电子工程，2016，36（1）：119-122.

[3]陈美伊，张鲲.粒子群算法优化特征和神经网络的模拟电路故障诊断[J].现代电子技术，2016，39（19）：140-143.

[4]杨清志，谢斌.基于遗传小波神经网络的模拟电路故障诊断方法[J].商丘师范学院学报，2015，31（12）：51-55，61.

[5]于文新，何怡刚，吴先明，等.基于果蝇-构造小波神经网络模拟电路诊断方法[J].计算机工程与应用，2015，51（22）：22-27.

[6]颜学龙，丁鹏，马峻.基于狼群算法的RBF神经网络模拟电路故障诊断[J].计算机工程与应用，2017，53(19)：152-156.

[7]乔维德.无刷同步发电机旋转整流器故障的神经网络识别[J].温州职业技术学院学报，2016，16（4）：44-48.

[8]乔维德，周晓谋.一种井下瓦斯传感器故障辨识方法[J].石家庄学院学报，2017，19（3）：46-52.

[9]乔维德.一种改进的提升机同步电机直接转矩控制[J].盐城工学院学报，2017，30（1）：28-33.

[10]乔维德.基于果蝇-蛙跳模糊神经网络PID的永磁直线同步电机控制[J].电机与控制应用，2017，44（11）：55-60.