基于嵌套Logit选择模型的城市配送自提柜选址路径问题

邱晗光，周愉峰

(重庆工商大学 物流管理系，重庆 400067)(*通信作者电子邮箱qiuhanguang@ctbu.edu.cn)

0　引言

末端交付方式(Last-mile Delivery)和配送时间窗(Time Slot)是顾客选择城市配送服务的重要决策选项，也是约束城市配送服务效率和成本的重要因素[1-2]。现有末端交付方式包括：送货上门(Attended-Home-Delivery, AHD)、自提柜(Reception Box, RB)和自提点(Collection and Delivery Point, CDP)等[1-2]。随着电子商务及餐饮、生活服务、零售等“线上到线下”(Offline to Offline, O2O)商业形态的快速崛起，顾客对末端交付方式与交付时间越来越敏感，面对不同的配送选项，选择决策往往具有相关性[3]。例如，顾客选择送货上门服务时，由于物品交接需要有人值守，往往对配送准时性要求较高，不同配送时间窗之间替代性较小；顾客选择自提柜服务时，由于物品交接无需有人值守，往往对配送准时性要求较低，通常仅仅约束配送到达的最晚时间，不同配送时间窗之间的替代性较大。在设计配送方案时，需要考虑末端交付方式和配送时间窗之间的相关性，优化设计自提柜选址、配送时间窗配置以及与之密切联系的路径规划，在保证配送方案路径可行性的同时，实现城市配送供需方双赢。

目前对城市配送服务顾客选择行为的研究主要采用多项选择模型(Multinomial Choice Model)。对于不同配送时间窗的选择性偏好，文献[4]考虑了时间窗定价、时间窗宽度等因素对顾客选择行为的影响，构建了顾客时间窗选择概率模型[4]；对于自提柜选址，文献[5-6]采用多项选择模型刻画顾客对于自提点的有限理性选择行为，考虑了自提点拥堵情形、顾客取货距离和自提点吸引力等因素。从已有文献看，目前还缺乏同时考虑末端交付方式和配送时间窗对顾客选择行为影响的研究，也没有涉及这类服务选项具有相关性的情形。

关于自提柜选址问题研究，国外研究以定性分析为主，国内研究主要采用集合覆盖模型、全面空间作用模型、双层规划模型、多目标选址模型进行研究[3]。后来，有限理性和消费者选择理论被引入到自提柜选址研究中。例如：文献[5]考虑顾客取货距离和自提柜的吸引力，构造了顾客对自提柜的分段效用函数，并引入Erlang-B模型描述自提柜拥堵情形，构建了考虑顾客有限理性的自提柜选址模型；文献[7]使用嵌套Logit模型描述顾客对于送货上门和自提柜服务的选择行为，在不考虑时间窗偏好的情形下，以单位时间运行成本最低和服务数量最大构建起多目标选址模型。以上研究没有将自提柜选址与配送时间窗分配联合优化考虑，忽略了自提柜具有的配送时间灵活性特征。

时间窗管理(Time Slot Management, TSM)是指末端交付环节不同区域配送时间窗的分配问题。时间窗分配对末端配送成本有较大影响，弱时间窗约束能够提高收益，完全无时间窗约束能够使总收益提升1/3左右[8]。以往城市配送或路径规划研究中往往将时间窗设定为外界变量。目前，时间窗管理研究主要面向送货上门方式，主要关注时间窗时长影响、时间窗分配、时间窗定价等问题。对于时间窗时长的影响，文献[9]发现将1 h的时间窗延长为2 h可以提高总收益6%[9]。对于时间窗分配，主要解决不同区域提供的时间窗以及订单接受决策，可以分为静态时间窗分配和动态时间窗分配两种情况。文献[10]假设不同配送区域的需求是已知的、需求与提供的配送时间窗无关，构建了时间窗顺序优化模型(Time Slot Schedule Design Problem, TSSDP)，解决了不同配送区域时间窗分配、时间窗的数量与时长等问题；文献[11]假设每个区域的需求已知并且独立于时间窗，研究了静态情形下时间窗在地理位置维度上的分配问题，使用连续预估方法估计路径成本；文献[12]在交通通行时间随机的情况下讨论了几种城市配送服务订单接受策略，在满足路径可行性的基础上接受尽可能多的配送服务订单。关于时间窗定价的研究也是面向送货上门服务。例如，文献[13]基于消费者选择模型，在配送数量和收益固定的情形下，讨论了如何利用价格折扣吸引顾客选择配送成本低的时间窗，其定价策略是基于当前已接受的订单，利用插入算法进行成本预估；文献[1]基于插入算法进行成本预估，不仅考虑当前已经接受的配送服务订单，还考虑未来可能到达的服务需求，研究了不同时间窗的动态定价问题；文献[14]建立了Logit选择模型，在配送能力外生的情形下，提出配送时间窗定价模型，讨论了运输能力预留策略。目前，关于时间窗管理的研究是城市末端配送领域的研究热点[15]，时间窗管理研究主要面向送货上门交付方式，通常假设每个区域的需求是预知的并且独立于时间窗。考虑多种末端交付方式与配送时间窗分配联合决策的研究还比较少，也很少从配送路径规划层面考虑不同配送点配送时间窗的可行性。

定位-路径问题(Location Routing Problem, LRP)，是运营层面和运作层面联合优化的代表性问题之一，产生了大量的研究成果[16]。这些成果主要考虑配送中心或车场选址，即配送车辆的起点与终点，对于自提柜选址-路径规划问题的研究较少。文献[17]在不考虑顾客时间窗偏好的情形下，建立了集送货上门和自提柜服务于一体的多容量终端选址——多车型路径集成优化模型，并设计一种先“多容量选址-分配”再“多车型路径”的两阶段模拟退火启发式算法。

综上，鉴于顾客在选择末端交付方式和交付时间窗时决策的相关性，本文基于嵌套Logit选择模型刻画顾客选择行为，然后将自提柜选址-时间窗分配-路径规划问题进行集成优化，试图解决在哪些位置开设自提柜、哪些区域提供自提服务、哪些区域提供送货上门、配送点的时间窗如何分配、车辆行驶路径如何安排等问题。

1　问题描述

考虑送货上门和自提柜两种末端交付方式，在单一配送中心-多个候选自提柜-多个配送点的路径网络结构中，研究自提柜选址-时间窗分配-路径规划问题(Reception Box Location-Time Slot Allocation-Vehicle Routing Problem， RBL-TSA-VRP)，如图1所示。

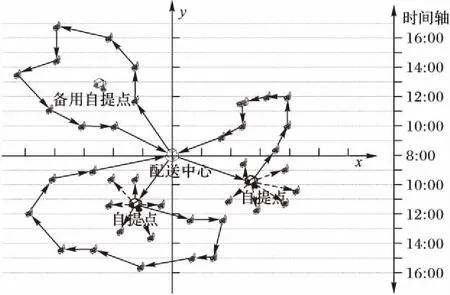
图1　自提柜选址-时间窗分配-路径规划问题Fig. 1　Reception box location-time slot allocation-vehicle routing problem

RBL-TSA-VRP可以如下定义：已知配送网络的节点和路径、备选自提柜的位置及固定建设成本、节点在不同末端交付方式和配送时间窗下配送需求、车辆载重等信息，考虑车辆起点和终点均在配送中心的约束下，以服务成本最小化和配送数量最大化为目标，解决以下问题：1)自提柜建设数量和位置；2)各配送点的末端交付方式选择(送货上门或自提柜服务)；3)配送路径选择；4)各配送点的时间窗分配。

在RBL-TSA-VRP中，自提柜选址属于运作层面的优化问题，自提柜服务区域分配及车辆路径规划属于作业层面的问题，RBL-TSA-VRP将运作层面和作业层面问题集成考虑。

2　城市配送嵌套Logit选择模型

顾客在末端交付方式之间的选择行为与不同配送时间窗之间的选择行为存在差别。在面对送货上门与自提柜服务时，不同末端交付方式带来的感知效用是影响顾客选择的重要因素。在面对不同配送时间窗时，实际需求时间是决定顾客选择的重要因素之一。为了区分顾客在选择末端交付方式和配送时间窗的相关性，使用两层嵌套Logit选择模型描述顾客选择城市配送服务的行为，如图2所示。

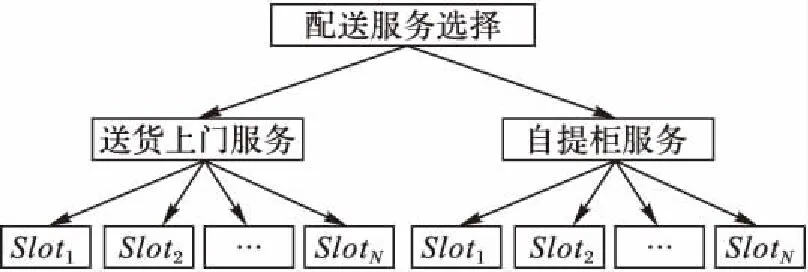
图2　城市配送两层嵌套Logit选择模型Fig. 2　Two-tier nested Logit model for urban distribution

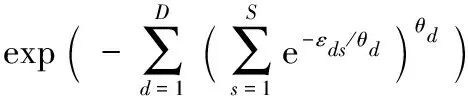
Ld与两种末端交付方式对应的顾客服务体验相关，体现在自提柜距离、客户隐私等方面。主要考虑自提柜距离的影响，假设Ld与自提柜距离r呈负相关的线性关系，即Ld=-αr。其中：送货上门d=1可以视为自提柜距离为0的特殊情形；α是距离影响因子。

Tds与配送货物的类别及顾客心理相关，体现在餐食、食品、日用品等配送物品类别差异、顾客心理、配送价格等方面。主要考虑实际配送时间窗与期望配送时间窗之间配送时间差tds的影响，假设Tds与配送时间差tds呈负相关的线性关系，即Tds=-βtds，其中β是时间误差影响因子。

在顾客追求自身效用最大化的情形下，顾客选择第D种交付方式的概率如式(1)所示：

(1)

顾客选择第D种交付方式下第s个时间窗进行配送的概率如式(2)所示：

(2)

3　城市配送自提柜选址-路径问题模型

3.1　符号定义

G=(N,A)代表完整的有向图，表示整个配送网络；

N代表节点集，N=N0∪Nd∪Nc，其中N0代表配送中心，Nd代表备选自提柜集合，Nc代表配送节点集合；

A代表弧集，A={(i,j):i,j∈N,i≠j}；

dij代表弧(i,j)的行驶距离；

tij代表弧(i,j)的行驶时间；

tsi代表配送节点i的服务时间，i∈Nc；

tai代表配送节点i的到达时间或配送时间，i∈Nc；

S代表配送时间窗集合，S={(es,ls)}，其中s=0表示无时间窗约束，e代表开始服务的最早时间，l代表停止接受服务的时间；

qis代表配送节点i在时间窗s的配送服务需求；

K={1,2,…,k}代表配送中心的车辆集合；

Fd代表在候选点d设置自提柜的固定费用，其中d∈Nd；

Fv代表使用车辆的固定费用；

c代表单位配送距离的成本；

C代表车辆载重能力。

3.2　决策变量

网络行驶方案：

(3)

网络配送方案：

(4)

(5)

3.3　目标函数

决策目标Ⅰ：配送数量最大化。

记配送数量为Q，根据嵌套Logit选择模型，各节点的需求数量取决于末端交付方式及实际配送时间。

(6)

决策目标Ⅱ：配送成本最小化。

(7)

其中:第一项表示运输成本，第二项表示启用车辆的固定成本，第三项表示启用自提柜的固定成本。

3.4　约束条件

约束(8)表示所有的节点都被服务，且送货上门和自提柜服务有且仅有一项。

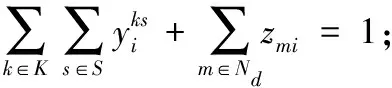
(8)

约束(9)表示网络节点流量平衡。

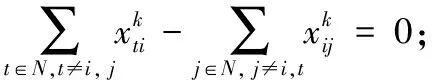
(9)

约束(10)表示所有车辆必须从配送中心出发并回到配送中心。

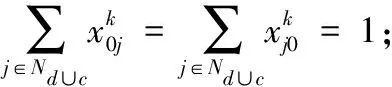
(10)

约束(11)表示送货上门服务的节点必须有车辆进入和离开。

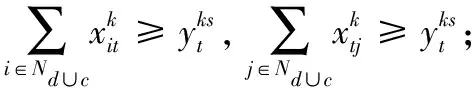
(11)

约束(12)表示选中的自提柜必须有车辆进入和离开。

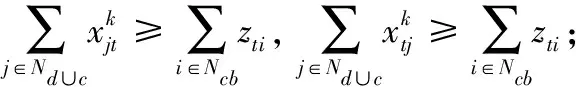
(12)

约束(13)表示车辆载重约束。

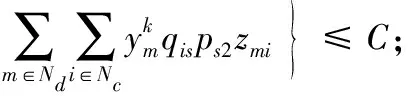
(13)

约束(14)表示车辆到达时间。

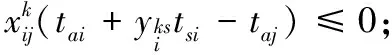
(14)

约束(15)避免车辆出现子回路,其中Vk表示车辆k访问的包含配送中心的节点集合。

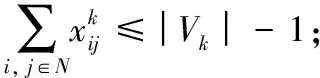
(15)

约束(16)～约束(18)表示决策变量的取值范围。

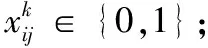
(16)

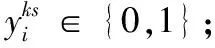
(17)

zmi∈{0,1}; ∀m∈ND,i∈NC,k∈K

(18)

4　算法设计

由于集成了整数规划和多目标规划，构建的城市配送自提柜选址-路径规划模型的求解难度大于单纯的自提选址问题和带时间窗车辆路径问题。根据文献[18]，依托多目标粒子群优化(Multiple Objective Particle Swarm Optimization, MOPSO)算法构造全局搜索算法，获取问题的帕累托解集[18-19]。MOPSO算法采用非支配排序、动态网格和拥挤距离等策略，设计了合理的帕累托集多样性维持策略和粒子群全局最优值更新操作用于多目标问题求解[20-21]。

4.1　编码方式

编码方式是粒子群群算法用于路径优化的首要问题之一。根据RBL-TSA-VRP特点，每个初始解的编码由三个部分构成：自提柜选址、自提柜服务区域分配和车辆行驶路径。假设备选自提柜集合Nd的数量为n，配送节点集合Nc的数量为m，则每个初始解的编码维度为1+n+3×m维。

1)自提柜选址编码。自提柜选址编码由1+m维表示。其中，m维对应m个备选自提柜，采用实数编码方式；第1+m维代表备选点选择阈值，当备选自提柜对应维度的实数值大于备选点选择阈值时，该备选点将建立自提柜。例如，拥有5个备选自提柜的选址编码如表1所示，前5个维度分别对应5个备选自提柜，第6个维度对应备选点选择阈值，则该编码的含义为1号和5号备选点将建立自提柜。

表1　自提柜选址编码实例(5个备选点)Tab. 1　Coding example for reception box location (5 alternate nodes)

2)自提柜服务区域分配编码。自提柜服务区域分配由m维表示，m维对应m个备选自提柜，采用实数编码方式。每个维度上的实数值代表对应备选点的辐射半径，即在辐射半径范围内的节点仅提供自提服务。该服务半径仅在对应备选点被选中建立自提柜的情形下有效。

3)车辆行驶路径编码。车辆行驶路径编码参考文献[21]，由m+n维表示，分别代表m个备选自提柜和n个节点。在剔除未被选中的自提备选点后，对于向量的每一维，其整数部分表示所在的车辆，整数部分相同的表示由同一辆车配送，小数部分的升序排列表示节点在该车辆中配送的次序。

4.2　算法流程

MOPSO算法流程如图3所示。

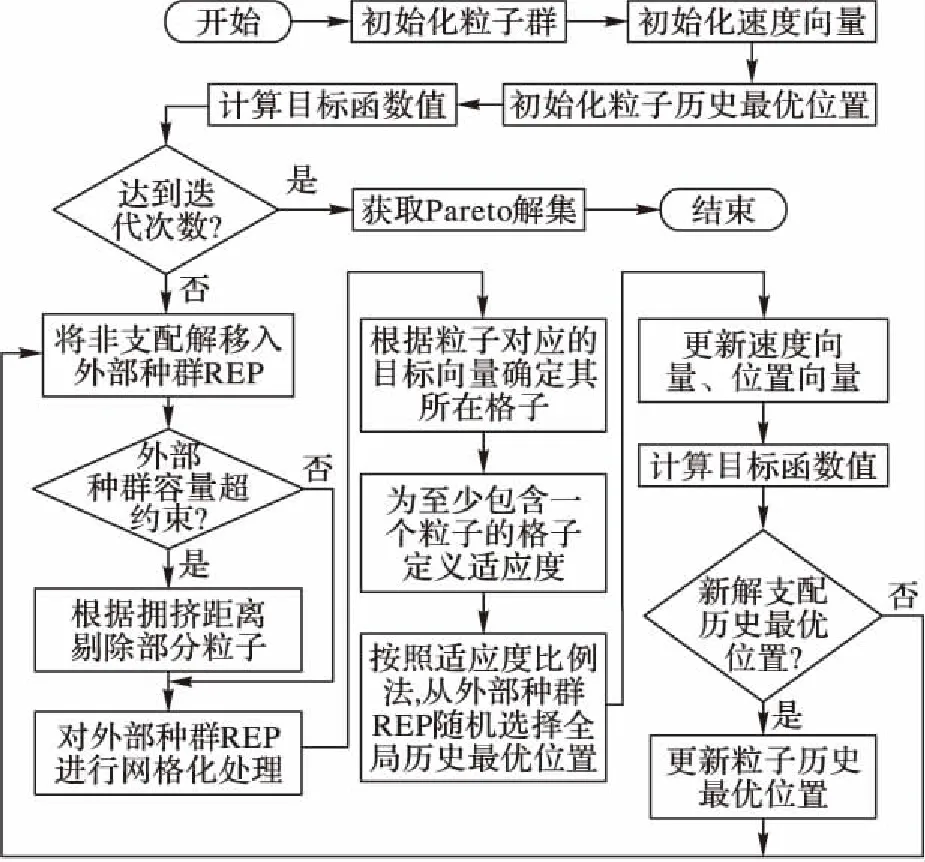
图3　MOPSO算法流程Fig. 3　Flow chart of MOPSO algorithm

MOPSO算法流程如下：

步骤1初始化。初始化外部粒子群、速度向量和粒子历史最优位置：粒子速度初值为0，粒子历史最优位置等于粒子初始位置，分别计算配送数量和配送距离目标函数值，初始化外部粒子群为空，迭代次数设置为0。

步骤2算法结束条件判断。若进化次数达到既定次数，则以获取的外部粒子群作为帕累托解集，结束算法；若未达到既定次数，转步骤3执行。

步骤3根据非支配排序，将非支配解移入外部粒子群中[18]。

步骤4判定外部粒子群容量限制。若超出容量限制，根据拥挤距离进行排序[18]，剔除多余粒子。

步骤5通过动态网格产生全局最优位置。首先以配送数量和配送距离构建二维网格，对外部粒子群进行网格化处理；为至少包含一个粒子的网格进行适应度赋值，所附适应度等于某个固定值除以网格内粒子数量；然后使用适应度比值法，确定某个网格；最后随机从该网格中挑选全局历史最优位置。

步骤6更新速度向量和位置向量。

步骤7计算新种群的目标函数值。

步骤8根据新解是否支配粒子历史最优位置，更新粒子历史最优位置，转向步骤2。

4.3　初始种群的构造

根据问题特点，自提柜服务区域分配和车辆行驶路径均依赖于自提柜选择，因此首先随机产生自提柜备选点选择阈值和各备选点对应维度的实数值，确定自提柜选址；然后随机产生服务半径，形成自提柜服务区域；最后，产生配送路径实数串，形成配送路径。此方法可以保证初始种群满足约束，提高初始种群在有效解空间内的分布密度，提升种群质量。

4.4　约束处理

RBL-TSA-VRP涉及的约束众多，包括服务约束、网络节点流量平衡、车辆起始点、到达时间、子回路约束等。根据编码方案，每个车辆访问点对应一个权重，配送车辆编号和顺序通过权重整数部分和小数部分分离，以整数部分作为车辆编号，以小数部分的升序排列作为车辆访问顺序，较容易满足路径网络流及车辆起始点的相关约束。需要额外处理的约束主要是车辆载重约束，采用罚函数方法解决。

5　仿真结果分析

5.1　算例数据

由于RBL-TSA-VRP是新的集成优化问题，本文以带时间窗车辆路径问题Soloman标准库中RC201算例和RC203算例为基础构建测试算例。算例涉及的相关参数如表2所示。MOPSO算法采用Matlab R2016a编程实现，运行平台采用Core i7- 6700 3.40 GHz 处理器,16 GB内存,Windows 10专业版操作系统。

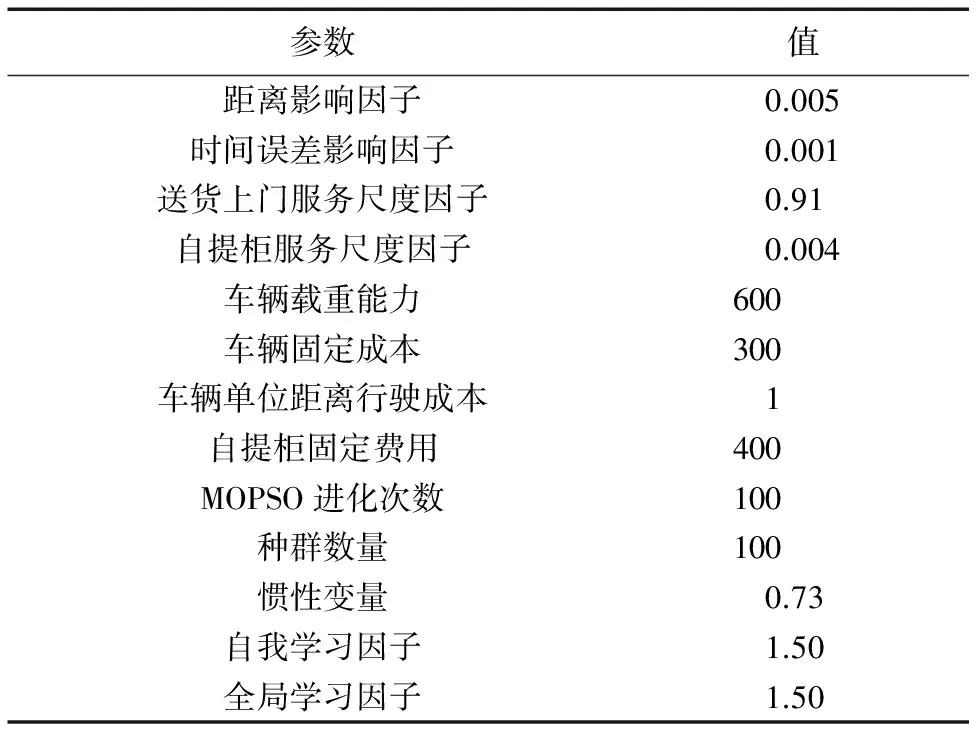
表2　相关参数设置Tab. 2　Parameter setting in the algorithm

5.1.1RC201算例

RC201算例总共用有100个节点，节点的分布呈现随机和聚集相结合的趋势，其位置分布如图4(a)所示。设计的算例从图中6个节点较密集的区域中选择了16个节点作为自提柜备选点。

5.1.2RC206算例

RC206算例总共用有50个节点，其位置分布如图4(b)所示。设计的算例从图中5个节点较密集的区域中选择了10个节点作为自提柜备选点。

5.2　算例求解结果

5.2.1MOPSO算法收敛情况

MOPSO算法获取的RC201算例的帕累托解集如图5(a)所示,RC206算例的帕累托解集如图5(b)所示，其中横轴表示配送服务成本，纵轴表示配送满足的需求数量，叉号点集为算法获取的帕累托解(Pareto)集合，圆点集为粒子群算法的种群集合。从图5可知，帕累托解集中无法分离出在配送成本最小化和配送数量最大化两个目标上均占优的解。

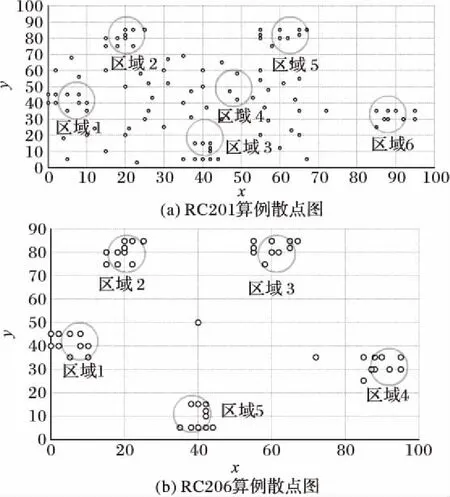
图4　RC206和RC201算例散点图Fig. 4　Customer locating in RC206 and RC201 instances

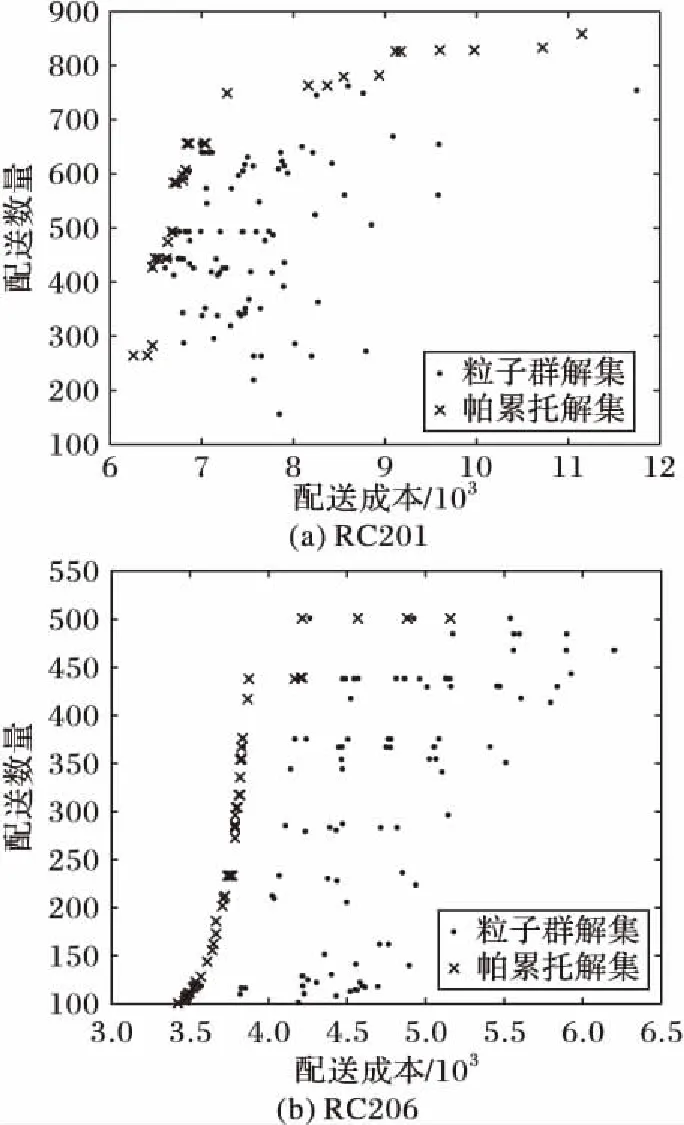
图5　配送数量最大化和成本最小化的帕累托解集Fig. 5　Pareto sets of maximizing the delivery amount and minimizing the total cost

RC206算例在成本最小偏好下，使用3辆车进行配送，启用3、12、21、31、40共5个自提点，总成本为3 241，实现配送数量100.515。车辆路径方案如表3所示，自提点服务方案如表4所示，其中1号点为配送中心，即车辆起始点和终止点。

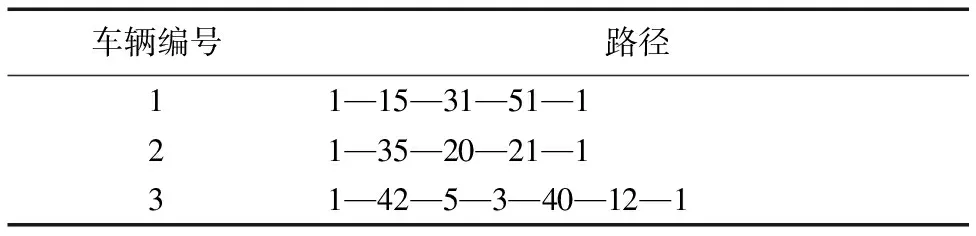
表3　车辆路径方案(RC206)Tab. 3　Vehicle routing of example RC206

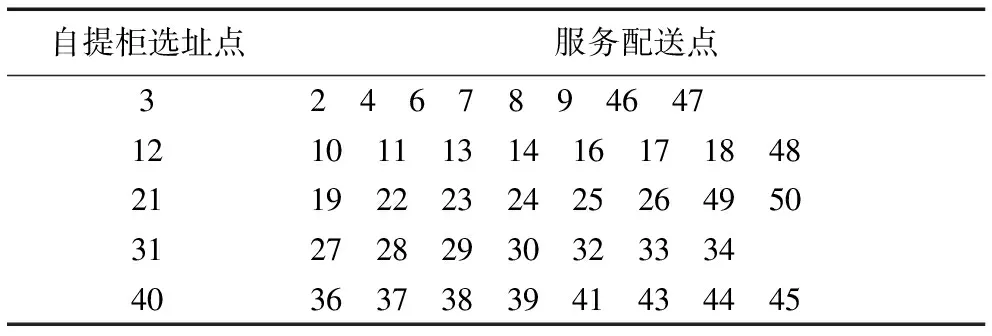
表4　自提柜选址(RC206)Tab. 4　Reception box locating of example RC206

5.2.2MOPSO算法性能对比测试

为了分析MOPSO算法求解多目标优化问题的性能，采用遗传算法(Genetic Algorithm, GA)进行对比分析。RC201和RC206算例获取的帕累托前沿如图6所示。由图6(a)可知，在RC201算例中，若偏好降低配送成本，MOPSO算法能够获取配送成本更低的帕累托解，如图中区域1所示；若偏好配送数量最大，GA能够获取配送数量更多的帕累托解，如图中区域2所示。在RC206算法中，MOPSO算法获取的帕累托前沿位于GA上方，无论是偏好最大化配送数量，还是偏好最小化配送成本，MOPSO获取的帕累托解集均优于GA。

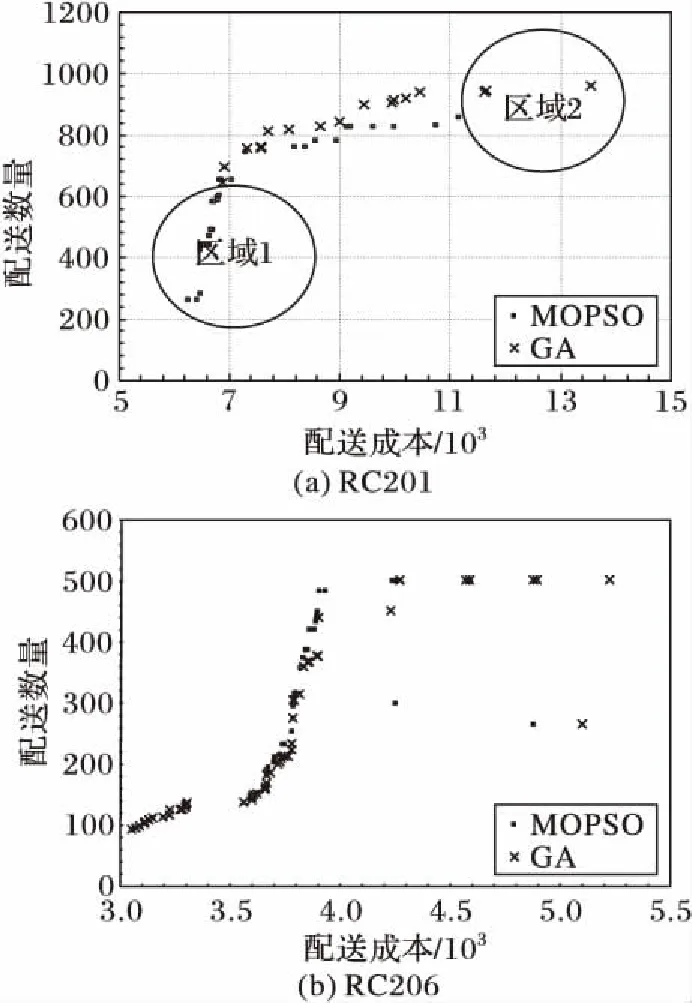
图6　帕累托前沿对比Fig. 6　Pareto frontier comparison

5.3　送货上门服务尺度因子θ1的影响分析

送货上门服务尺度因子θ1用于衡量送货上门不同服务时间窗未观察到的效用之间相互独立程度，表示顾客在选择不同时间窗的替代性。θ1越大，表明不同时间窗差异越大；当θ1接近1时，随机扰动项相互独立，不同配送时间窗之间的替代性最小。

图7展示了RC201算例和RC206算例中送货上门服务尺度因子对配送数量和配送成本的影响。随着送货上门服务尺度因子θ1从0.01逐渐上升到1.11，顾客选择仅在[0.01,1]区间内保证效用最大化，顾客选择在不同配送时间窗之间的替代性越小，实际服务时间差对配送需求的影响越大。无论是追求配送成本最小化、还是配送数量最大化，获取的最优方案均倾向于提高配送的准时性，配送满足的需求数量逐渐上升，配送成本呈现震荡上升态势。

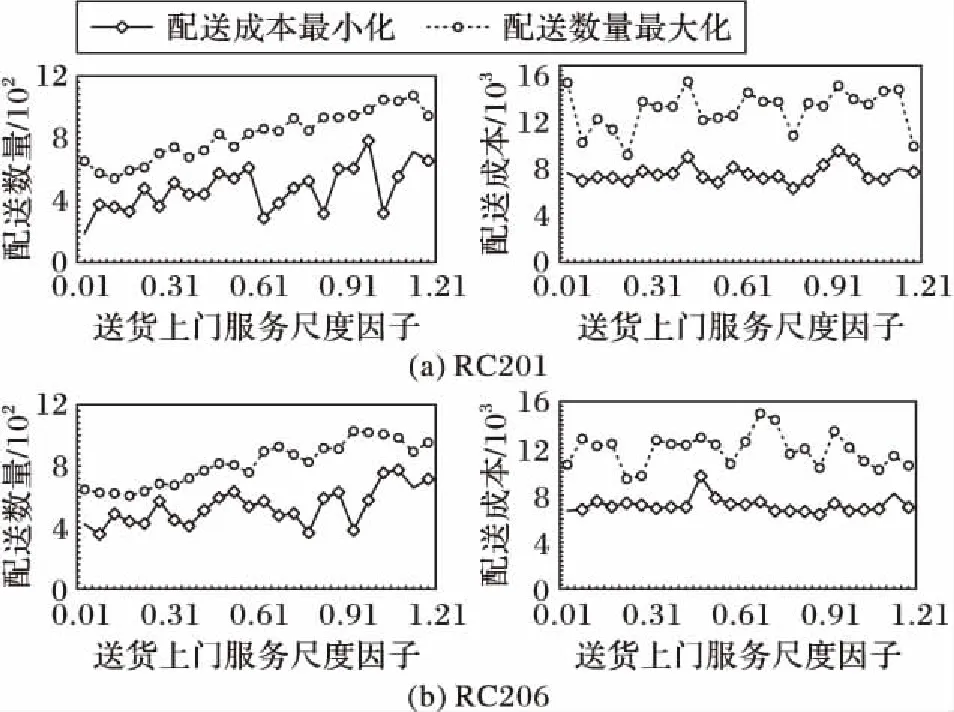
图7　送货上门服务尺度因子θ1对配送数量和配送成本的影响Fig. 7　Impact of AHD independence parameter θ1 on delivery amount and delivery cost

5.4　自提柜服务尺度因子θ2的影响分析

自提柜服务尺度因子θ2用于衡量自提柜服务时不同服务时间窗未观察到的效用之间相互独立程度，表示顾客在选择不同时间窗的替代性。θ2越大，表明不同时间窗差异越大，当θ2接近1时，随机扰动项相互独立，不同配送时间窗之间替代性最小。

图8展示了RC201算例和RC206算例中自提柜服务尺度因子对配送数量和配送成本的影响。随着自提柜服务尺度因子θ2从0.01逐渐上升到1.11，顾客选择仅在[0.01,1]区间内保证效用最大化，顾客在不同配送时间窗之间的替代性越小，实际服务时间差对配送需求的影响越大。不同于送货上门服务，无论是追求配送成本最小化，还是配送数量最大化，获取的最优方案均降低配送的准时性。配送数量逐渐下降，配送成本呈现震荡下降趋势。

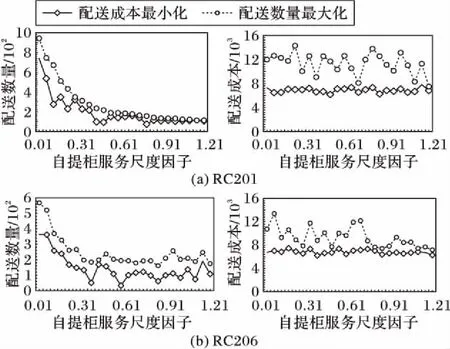
图8　自提柜服务尺度因子θ2对配送数量和配送成本的影响Fig. 8　Impact of RD independence parameter θ2 on delivery amount and delivery cost

6　结语

城市配送中顾客在选择末端交付方式和配送时间窗时，不同配送服务选项相互联系，这种相关性对城市配送诸多运作决策带来了挑战。自提柜选址决定了不同配送点可供选择的末端交付方式，路径规划决定了不同配送点可行的送达时间窗，自提柜选址、配送时间窗分配与路径规划之间存在紧密的联动关系。鉴于此，基于嵌套Logit选择模型刻画顾客面对配送服务选项的相关性选择行为，以配送数量最大化和配送成本最小化为目标，将自提柜选址-时间窗分配-路径规划问题进行集成优化。研究表明：随着送货上门服务尺度因子逐渐增大，顾客需求在不同配送时间窗之间的替代性越小，无论是追求配送成本最小化，还是追求配送数量最大化，配送数量逐渐上升，获取的最优方案倾向于提高配送的准时性；相反，随着自提柜服务尺度因子逐渐增大，不同于送货上门服务，获取的最优方案均降低提高配送的准时性，导致配送数量逐渐下降。本文在求解中主要使用了基于动态网格和拥挤距离的多目标粒子群算法，下一步将考虑基于问题特点，丰富搜索的领域结构设计，进一步提升算法求解质量。

参考文献:

[1]YANG X, STRAUSSY A K, CURRIEZ C S M, et al. Choice-based demand management and vehicle routing in e-fullment [J]. Transportation Science, 2014, 50(2): 473-488.

[2]WANG X, ZHAN L, RUAN J, et al. How to choose “last mile” delivery modes for e-fulfillment [J]. Mathematical Problems in Engineering, 2014, 2014: Article ID 417129.

[3]张锦,陈义友.物流“最后一公里”问题研究综述[J].中国流通经济,2015(4):23-32. (ZHANG J, CHEN Y Y. The review of research on the “last-mile” in logistics [J]. China Business and Market, 2015(4): 23-32.)

[4]陈淮莉,魏云飞.考虑客户满意度的网络零售配送时隙定价策略[J].计算机工程与应用,2016,52(19):1-6, 106. (CHEN H L, WEI Y F. Pricing strategy of time slot for Internet retailing delivery with considering customer satisfaction [J]. Computer Engineering and Applications, 2016, 52(19): 1-6.)

[5]陈义友,张锦,陈以衡,等.基于顾客有限理性的自提点选址研究[J].工业工程与管理,2015,20(6):92-100. (CHEN Y Y, ZHANG J, CHEN Y H, et al. Research on pickup point location based on customers’ bounded rationality [J]. Industrial Engineering and Management, 2015, 20(6): 92-100.)

[6]陈义友,张锦,曾倩,等.基于顾客选择的自提点选址双层规划模型[J].管理学报,2016,13(12):842-1850. (CHEN Y Y, ZHANG J, ZENG Q, et al. Bi-level optimization model for pickup point location under customer choices [J]. Chinese Journal of Management, 2016, 13(12): 1842-1850.)

[7]陈义友,韩珣,曾倩.考虑送货上门影响的自提点多目标选址问题[J].计算机集成制造系统,2016,22(11):2679-2690. (CHEN Y Y, HAN X, ZENG Q. Multi-objective pickup point location problem considering impact of home delivery [J]. Computer Integrated Manufacturing Systems, 2016, 22(11): 2679-2690.)

[8]PUNAKIVI M, SARANEN J. Identifying the success factors in e-grocery home delivery [J]. International Journal of Retail & Distribution Management, 2001, 29(4): 156-163.

[9]CAMPBELL A M, SAVELSBERGH M W P. Decision support for consumer direct grocery initiatives [J]. Transportation Science, 2005, 39(3): 313-327.

[10]AGATZ N, CAMPBELL A, FLEISCHMANN M, et al. Time slot schedule design for e-fulfillment [R]. Rotterdam, Netherlands: Rotterdam School of Management Erasmus University, 2007.

[11]AGATZ N, CAMPBELL A, FLEISCHMANN M, et al. Time slot management in attended home delivery [J]. Transportation Science, 2011, 45(3): 435-449.

[12]EHMKE J F, CAMPBELL A M. Customer acceptance mechanisms for home deliveries in metropolitan areas [J]. European Journal of Operational Research, 2014, 233(1): 193-207.

[13]CAMPBELL A M, SAVELSBERGH M. Incentive schemes for attended home delivery services [J]. Transportation Science, 2006, 40(3): 327-341.

[14]陈淮莉,汪健.能力预留的网络零售配送时隙分配与定价研究[J].中国科技论文,2016,11(7):765-771. (CHEN H L, WANG J. Allocation and pricing of time slot for Internet retailing with capacity reservation [J]. China Sciencepaper, 2016, 11(7): 765-771.)

[15]许茂增,余国印.城市配送研究的新进展 [J].中国流通经济,2014(11):29-36. (XU M Z, YU G Y. Literature review of internal and external research literature on the urban distribution [J]. China Business and Market, 2014(11): 29-36.)

[16]NAGY G, SALHI S. Location-routing: Issues, models and methods [J]. European Journal of Operational Research, 2007, 177(2): 649-672.

[17]周林,林云,王旭,等.网购城市配送多容量终端选址与多车型路径集成优化[J].计算机集成制造系统,2016,22(4):1139-1147. (ZHOU L, LIN Y, WANG X, et al. Integrated optimization for multiclass terminal location-heterogeneous vehicle routing of urban distribution under online shopping [J]. Computer Integrated Manufacturing Systems, 2016, 22(4): 1139-1147.)

[18]李中凯,谭建荣,冯毅雄,等.基于拥挤距离排序的多目标粒子群优化算法及其应用[J].计算机集成制造系统,2008,14(7):1329-1336. (LI Z K, TAN J R, FENG Y X, et al. Multi-objective particle swarm optimization algorithm based on crowding distance sorting and its application [J]. Computer Integrated Manufacturing Systems, 2008, 14(7): 1329-1336.)

[19]凌海风,周献中,江勋林,等.改进的约束多目标粒子群算法[J].计算机应用,2012,32(5):1320-1324. (LING H F, ZHOU X Z, JIANG X L, et al. Improved constrained multi-objective particle swarm optimization algorithm [J]. Journal of Computer Applications, 2012, 32(5): 1320-1324.)

[20]陈民铀,张聪誉,罗辞勇.自适应进化多目标粒子群优化算法[J].控制与决策,2009,24(12):1851-1855,1864. (CHEN M Y, ZHANG C Y, LUO C Y. Adaptive evolutionary multi-objective particle swarm optimization algorithm [J]. Control and Decision, 2009, 24(12): 1851-1855,1864.)

[21]吴斌,倪卫红,樊树海.开放式动态网络车辆路径问题的粒子群算法[J].计算机集成制造系统,2009,15(9):1788-1794. (WU B, NI W H, FAN S H. Particle swarm optimization for open vehicle routing problem in dynamic network [J]. Computer Integrated Manufacturing Systems, 2009, 15(9): 1788-1794.)