行驶时间随机的分批配送车辆路径问题模型与算法

石建力，张　锦

(1.西南交通大学 交通运输与物流学院，成都 610031；　2.西南交通大学 综合交通运输智能化国家地方联合工程实验室，成都 610031)(*通信作者电子邮箱shjl20043528@163.com)

0　引言

随着顾客期望值增高以及众多以顾客为导向的商业模式的出现[1]，在城市配送中考虑配送时间、配送效率越来越引起研究者关注。带时间窗的车辆路径问题(Vehicle Routing Problem， VRP)、以配送时间为目标的VRP以及以综合费用(包括时间费用等)为目标的VRP等研究越来越得到重视。在实际的配送过程中，红绿灯的变换、城市道路限行等常规因素，以及道路拥堵、道路维修、车辆损坏等意外因素都会引起行驶时间的不确定[2]。此时的情形与确定情形不同，需要对配送路径进行合理规划和优化，以提高配送效率，降低配送费用。本文将行驶时间随机引入分批配送车辆路径问题(Split Delivery Vehicle Routing Problem， SDVRP)进行研究，建立行驶时间随机的带软时间窗的分批配送车辆路径问题(Split Delivery Vehicle Routing Problem with Time Window and Stochastic Travel Time，SDVRPTWSTT)带修正的随机规划模型，并根据问题特点设计改进的粒子群优化(Particle Swarm Optimization， PSO)算法进行求解。

SDVRP由Dror等[3]于1989年正式提出，是经典车辆路径问题的一类变型，在报纸配送、食品配送、零售物品配送、应急物资车辆路径问题等实际运作中广泛应用[4]。特别地，Frizzell等[5]首次对带时间窗的分配配送车辆路径问题(Split Delivery Vehicle Routing Problem with Time Windows，SDVRPTW)进行研究，提出使用局部搜索算法求解，并使用重定位和交换两个局部搜索算法优化构造的解；Ho等[6]提出使用禁忌搜索算法求解SDVRPTW，并且不对需求点分割加任何限制；Belfiore等[7]将巴西一个零售组织配送问题抽象为混合车辆的SDVRPTW，并使用分散搜索算法求解；McNabb等[8]将局部搜索算子使用到最小-最大蚁群系统中，对各个局部搜索算子的效率进行测试和对比研究。精确求解算法上，Salani等[9]分别使用分支定价法求解SDVRPTW；Desaulniers[10]使用一类新的分支定价切割法(branch-and-price-and cut)求解SDVRPTW，并得到较好结果；Archetti等[11]将禁忌搜索算法嵌入到分支定价切割法求解SDVRPTW。

以往的SDVRPTW基本都是研究确定性问题，行驶时间是确定的，随机分批配送车辆路径问题的研究成果较少。Bouzaiene-Ayari等[12]、Lei等[13]分别对需求随机的SDVRP进行研究，但目前尚无对SDVRPTWSTT的研究成果。

对行驶时间随机的车辆路径问题(Vehicle Routing Problem with Stochastic Travel Time，VRPSTT)有较多研究[14]。杨信丰等[15]研究带时间窗的VRPSTT，建立机会约束规划模型，并设计遗传算法进行求解。李锋等[16]建立VRPSTT的多目标模型，并设计混合遗传算法进行求解。王征等[17]建立带时间窗的VRPSTT多目标模型，并设计高效的启发式算法进行求解。李妍峰等[18]结合交通流量特征研究行驶时间随机的VRP，并设计新的路径更新策略进行求解。Ando等[19]对带软时间窗的VRPSTT进行研究，文中行驶时间分布函数由实际交通数据估计而来。Russell等[20]构建了带时间窗的VRPSTT多目标模型，分别以车辆数、总行驶距离和惩罚费用为约束设计禁忌搜索算法进行求解，并使用爱尔朗分布作为行驶时间的分布。Li等[2,21]研究软时间窗和硬时间窗的VRPSTT，并考虑了服务时间不确定的因素。对软时间窗情形，作者建立两阶段带修正的随机规划模型，目标为在第一阶段构建路径集、在第二阶段最小化期望费用对路径进行调整。为此，该文中设计禁忌搜索算法进行求解，假设行驶时间和服务时间都服从正态分布，并利用随机模拟求得期望。对硬时间窗情形，作者建立机会约束模型进行求解以保证车辆到达需求点时间窗的概率不小于某预设值，期望最早和最晚惩罚费用不包括在目标函数中。Zhang等[14]对带时间窗的VRPSTT进行研究，建立了以费用最小和按时到达概率最大的多目标模型。通过模型中顾客服务水平的约束可显式计算出每个顾客点准时送达的概率，而通过调整顾客服务水平约束值可方便研究费用与服务水平的对比。该文中设计了迭代禁忌搜索算法进行求解。Ta等[22-23]研究了软时间窗的VRPSTT，建立带修正的随机规划模型，同时考虑配送总费用(总行驶路径、车辆数以及期望超时费用)和服务费用(提前到达或迟到)，其中配送费用为实际费用，而服务费用为服务水平的代表。该文作者分别构建禁忌搜索算法和列生成、分支定价法进行求解。Ehmke等[24]针对带时间窗的VRPSTT建立以违背每个时间窗约束的概率为约束的机会约束模型，并以配送费用为目标函数。该文中提供了一种为所有需求点计算服务水平的方法，并计算每个需求点的开始服务时间及到达时间的分布。

多数求解VRPSTT的问题都要考虑时间窗，但很少在软时间窗下考虑等待时间问题。在现实配送过程中，很多时候即使客户时间窗为软时间窗，由于配送时间问题、文书问题等都将导致等待的情况发生，因此本文考虑软时间窗下等待的情况，此时比硬时间窗下更为复杂，因为等待随时都可能发生，而硬时间窗下只需考虑时间窗之前的等待时间。

求解VRPSTT使用最多的方法为现代进化算法，最常用的为禁忌搜索算法，目前尚无使用PSO算法求解SDVRPTWSTT的成果。PSO算法被应用于解决多类离散优化问题(包括带时间窗的VRPSTT)并取得了比较好的结果，与其他启发式算法相比，它具有信息交换充分、收敛快等优点[25-26]。在不允许分批配送的车辆路径问题[27-29]中，一般使用整数编码，即所有需求点序号的一个排列，所有粒子位置向量、速度向量长度均一致。本文考虑使用改进的PSO算法求解SDVRPTWSTT，与求解不允许分批配送的车辆路径问题的不同之处有两点：1)由于允许分批配送的原因，粒子编码中存在重复的需求点，其编码和解码过程均与不允许分批配送时不同。2)粒子位置向量更新过程中涉及到的位置向量、速度向量等长度有可能不统一，计算过程中将导致信息丢失或增加随机信息，影响算法效率和效果；其次，使用PSO算法求解车辆路径问题过程中，粒子位置向量需要在连续空间及离散空间之间进行转换，容易丢失信息，降低算法效率。这些均是本文需要解决的问题。

1　问题描述及模型建立

问题定义在无向图G=(V,A)上，其中：V={0,1,…,n}为节点集合，0代表车场；C={1,2,…,n}表示n个不同的需求点；A={(i,j):i,j∈V,i≠j}为边集合。

需求点i的需求量为di(di>0)为整数；第k辆车对需求点i的服务时间为sik(sik≥0)是随机变量，本文假设所有需求点的服务时间均服从正态分布，即sik～N(μik1,σik1)。所有节点均带有时间窗[ei,li]，其中：ei,li分别代表对需求点i开始服务的最早时刻和结束服务的最晚时刻；[e0,l0]代表车辆离开车场的最早时刻和返回车场的最晚时刻。时间窗为软时间窗，允许车辆在时间窗外开始服务，但在时间窗外开始服务需要产生额外惩罚费用。

本文将等待时间引入软时间窗VRP中，第k辆车在需求点i的等待时间记为wik，也是随机变量，为简化问题，假设等待时间也服从正态分布，即wik～N(μik2,σik2)。在实际生活中，时间窗内外都有可能产生等待，有时甚至会发生长时间等待的情况，如在给大超市进行配送时，零售商处于主导地位，配送企业可能需要等待较长时间，即使提前预约，有时也会需要等待1～2个小时。为简化问题，本文暂不对此种情况作考虑。等待将对配送过程及司机劳动强度产生影响，将此类影响统称为等待费用，其大小简化为与等待时间线性相关。

每条边具有对称的行驶距离cij和行驶时间tij，行驶距离满足三角不等式；每条边上的行驶时间tij为随机变量，假设所有边的行驶时间均服从正态分布，即tij～N(μij,σij)。

车辆集合为K={1,2,…,m}，所有车容量均相同，为Q。假设车辆数量无限，根据实际调研，即使某些时候配送企业车辆数不够用，但均有相应的应急处理方式，比如与其他配送企业签订战略协议，可随时借调车辆。某些需求点可能由多辆车服务。

符号说明见表1。

表1　变量符号说明Tab. 1　Variable symbol description

决策变量包括xijk和yik,其中xijk如下所示：

yik则为需求点i由车辆k进行配送的量。

目标函数为最小化综合费用。

随机规划模型如下：

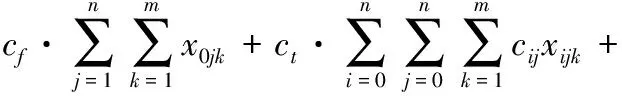
(1)

(2)

(3)

(4)

(5)

(6)

yik∈N;i=1,2,…,n,k=1,2,…,m

(7)

xijk∈{0,1};i=0,1,…,n,j=0,1,…,n,k=1,2,…,m

(8)

目标函数中期望延迟时间、期望提前时间和期望等待时间都是随机的，本文通过将这三个期望量通过推导表示为行驶时间、服务时间和等待时间期望与方差的解析表达式，以提高计算过程中目标函数计算效率。

1.1　服务时间性质

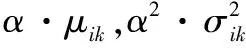
1.2　到达时刻和开始服务时刻性质

令Tij表示车辆经过弧(i,j)从需求点i到需求点j所需时间，则车辆k到达需求点j的时间ajk为直到需求点j所有边的行驶时间、需求点j之前的所有需求点的等待时间和服务时间之和，即：

其中：Ajk表示车辆k经过的直到需求点的j所有边；Cjk表示车辆k上需求点j之前的所有需求点；yik为车辆k对Cjk中需求点的配送比例。

根据正态分布的可加性，到达时间ajk也服从正态分布，其均值和方差分别为：

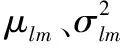
由于本文中假定车辆到达需求点不一定直接开始服务，因此，车辆开始服务的时间为ssjk=ajk+wjk，由正态分布的性质得，开始服务时间也服从正态分布，其均值与方差分别为：

1.3　目标函数计算

本文中假定行驶时间、服务时间、等待时间均服从正态分布，它们的概率密度函数和分布函数分别由下述两式给出：

其中：t≥0，δ≥0。

期望延迟时间可以根据以下过程计算得到：

所以：

同样的道理，期望提前时间也可计算出来：

2　改进的粒子群优化算法

2.1　问题描述

本文结合问题特点，将自适应选择和路径重连融入PSO算法进行求解：路径重连用于粒子位置更新，自适应选择用于速度更新。

在PSO算法初始阶段，一簇粒子随机产生，每个粒子对应一个解，在解空间中有一个固定的位置。在迭代过程中，每个粒子对应一个速度向量，并根据速度向量移动。设计成功PSO的关键是在位置向量和解之间寻找合适的映射。由于分批配送车辆路径问题中存在被分割的需求点，针对VRP的路径分割算法已不再适用，本文使用Boudia等[30]提出的改进的基于Bellman方程的路径分割算法分割路径。

经典PSO中粒子移动取决于速度向量，粒子位置向量需要在连续空间和离散空间之间进行转换，会丢失信息，降低随机路径问题的求解效率，影响解质量。本文使用路径重连策略进行位置更新以避免PSO算法中位置向量在离散空间与连续空间之间转换，提高求解效率。速度更新方程的角色有所转变，用于衡量粒子在路径重连过程中向自身最优、局部最优、全局最优进化的重要参数。粒子速度不再是粒子位置更新的主导，也减弱分批配送车辆路径问题中统一粒子位置向量、速度向量、局部最优、邻域最优和全局最优位置向量等向量非零元素个数而导致信息丢失或者增加无用信息带来的影响。

最后，本文使用基于变邻域搜索(Variable Neighborhood Search， VNS)算法的局部搜索策略对每个粒子进行优化以提高解的质量。在每次迭代中，粒子群中最优粒子和粒子自身最优被保存。本文求解最小化问题，目标函数值较大的解将被标记为劣解。算法在达到最大迭代次数时结束。

2.2　初始解生成

初始种群包含np个初始解，本文使用三种不同的方式生成整个初始解，其中：节约算法生成不产生需求点分割的1个初始解；改进扫描算法产生需求点分割的1个初始解；顺序插入算法生成np-2个允许分割的初始解。

1)节约算法。

此算法为经典的VRP算法，将每个需求点看作一条路径，然后通过连续的方式将距离最近的两个路径合并，从而得到VRP解。本文以此方式生成1个初始解，解中无需求点被分割，意在初始种群中放置较优的不产生分割的初始解。

2)改进的扫描算法。

扫描算法也是VRP经典算法，当一条路径的容量未被耗尽且无法容下下一个需要加入的需求点时，分割此需求点，一部分放入当前路径，剩余一部分放入下一条新路径。本文以此方式产生一个初始解，部分需求点被分割。

3)随机生成。

此算法随机生成一个需求点的序列，并依次将需求点添加到路径中，当前路径容量未被耗尽且无法容下下一个需求点的需求量时，将此需求点需求量分割，部分放在当前路径中，剩余部分放入下一条新路径中。本文以此方式产生np-2个初始解，这些解中有可能无需求点被分割，部分解中部分需求点被分割。

2.3　编码

本文中粒子采用整数编码，每个元素代表一个需求点，编码中可存在重复数字，表示此需求点需求被分割；每个粒子包含2*nc个元素，nc为需求点数量。由于本文使用路径重连算法对粒子位置进行更新，只需对粒子进行编码，不再需要将连续型编码转化为整型编码，只需在每次速度更新时将整型编码转换为连续型编码即可，转换的方式为每个元素除以需求点个数。

2.4　速度更新

本文使用基于全局、局部邻域最优的速度更新方程，方程中包括四项，因此粒子除了向新方向、自身最优、全局最优移动外，还会向局部最优移动，与局部最优粒子交换信息。通过添加第四项，避免解快速向初始全局最优解收敛，增加每个粒子通过局部最优找到全局最优的概率。速度更新方程如下：

vij(t+1)=χ1*(vij(t)+c1*rand1*(pbestij-xij(t))+

c2*rand2*(gbestij-xij(t))+

c3*rand3*(lbestij-xij(t)))

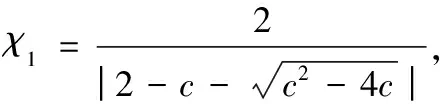
在分批配送车辆路径问题中，速度更新公式中的向量vij(t)、xij(t)、pbestij、gbestij、lbestij，除了vij(t)、xij(t)非零元素个数相同，其他向量之间非零元素个数均有可能不同，因此在速度更新公式中需要选择合适的向量长度进行计算。本文中采用自适应方式在粒子位置向量xij(t)、自身最优pbestij、全局最优gbestij和局部最优lbestij之间选取标准向量。

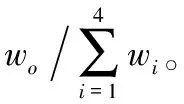
wo,N+1=wo,N(1-χ)+χπoN/εoN

其中:εoN、πoN分别代表向量o在第N阶段被选中的次数和所得的分数；χ∈[0,1]为常数，文中选取χ=0.1。

向量o在第N阶段的得分按下式计算，其中得到的解为在组合邻域拓扑阶段得到的解：

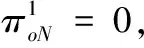
2.5　粒子位置更新

文中每个粒子位置通过路径重连进行更新，位置更新方程被路径重连过程替代，能这样做的原因为路径重连思想与PSO算法中粒子位置更新思想是相似的，也是决定粒子向自身最优、向全局最优和向局部最优等移动。

其中:itermax为迭代最大次数。ubound和lbound分别是每个粒子速度的上界和下界,一般地，ubound和lbound分别取4和-4。如果在某些迭代中，粒子速度某元素超出上下界，则在上下界中重新产生一个新的值。参数w1和w2值应比较大，以保证算法初始阶段L1尽量大，并随着迭代的进行减小；另外，L2需要比L1大，因此w2应大于w1。所以，本文设置w1=0.8，w2=0.9以保证不同移动方向拥有基本相同的概率。由于路径重连算法将导致解在较少次数的迭代中收敛到单个优解附近，因此与最优解相差10%以内的解均不接受[31]，除非能更新最优解。

在不允许分批配送的VRP中，一般在路径重连过程中使用交换算子进行局部搜索，本文中允许分批配送，因此使用Boudia等[30]提出的改进的允许分批配送的交换算子进行局部搜索。

2.6　粒子邻域最优更新

本文使用扩展邻域拓扑进行粒子局部邻域最优的更新。借鉴Marinakis等[32]将VNS邻域扩展的思想融入到扩展邻域的做法，根据解的质量调整粒子邻域，每个粒子的邻域根据自身解优化程度的不同而不同。开始阶段所有粒子邻域是相同的,当某个粒子对应的解在连续一定数量itnum的迭代过程中都没有被优化，只有它的邻域进行扩展。在此策略下，每个粒子邻域范围不同。当邻域范围扩展到整个空间时，局部最优邻域将从最小规模邻域重新初始化。

2.7　局部搜索算法

为了提高PSO算法解的质量，采用基于VNS的局部搜索策略。本文允许分批配送，在单条路径上执行2-opt、重定位、交换等局部搜索算子，在路径间执行分批1-1交换、分批2-1交换、路径添加、k-分割等算子。首先，选择局部搜索算法的数量，为了不增加算法复杂性，使用Marinakis在文献[31]中提出的策略，在每次迭代中使用一个局部搜索组合，因此选取VNS因子CVNS控制使用的局部搜索组合，通过随机数产生器randi(0,1)产生的随机数与CVNS进行比较：如果随机数小于或等于CVNS，则执行上述7个局部搜索算子中的第一个局部搜索算子；如果随机数小于或等于2*CVNS，则执行前两个局部搜索算子；以此类推。

2.8　出发时间调整

从PSO算法得到的解都是时刻0从车场出发，本文的后验优化算法将每辆车从车场出发的时间以M分钟循环调整，直到路径综合费用无法进一步降低为止。

3　算例分析

本文程序使用Matlab (2012b)编写，运行平台内存12 GB，显卡2.9 GHz，64位操作系统。

算例采用Solomon[33]提出的经典算例进行测试，该算例构造时考虑了需求点空间分布和时间窗的合理性等，被很多学者选为测试算例。考虑Solomon的四类算例：R1、R2、RC1和RC2，且算例规模为100。R1和RC1类算例时间窗较短，车辆只能服务较少的需求点；R2及RC2类算例具有长时间窗，允许车辆对更多的需求点进行配送。在所有的测试中，期望行驶时间等于相应的欧几里得距离。

3.1　算例调整

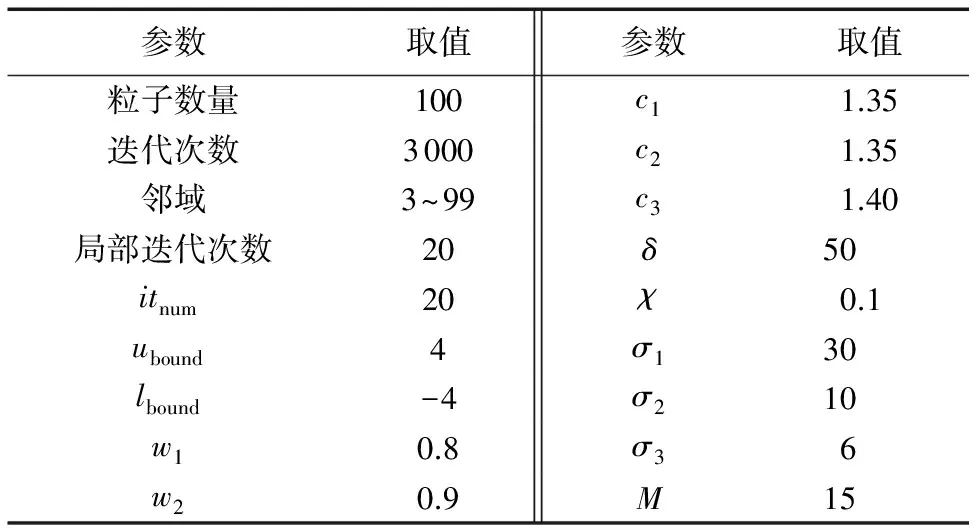
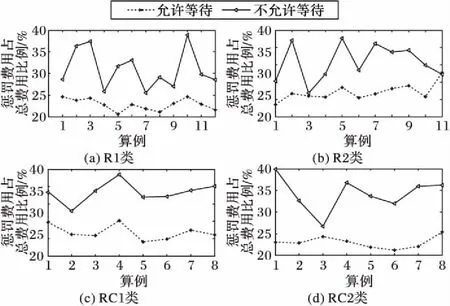
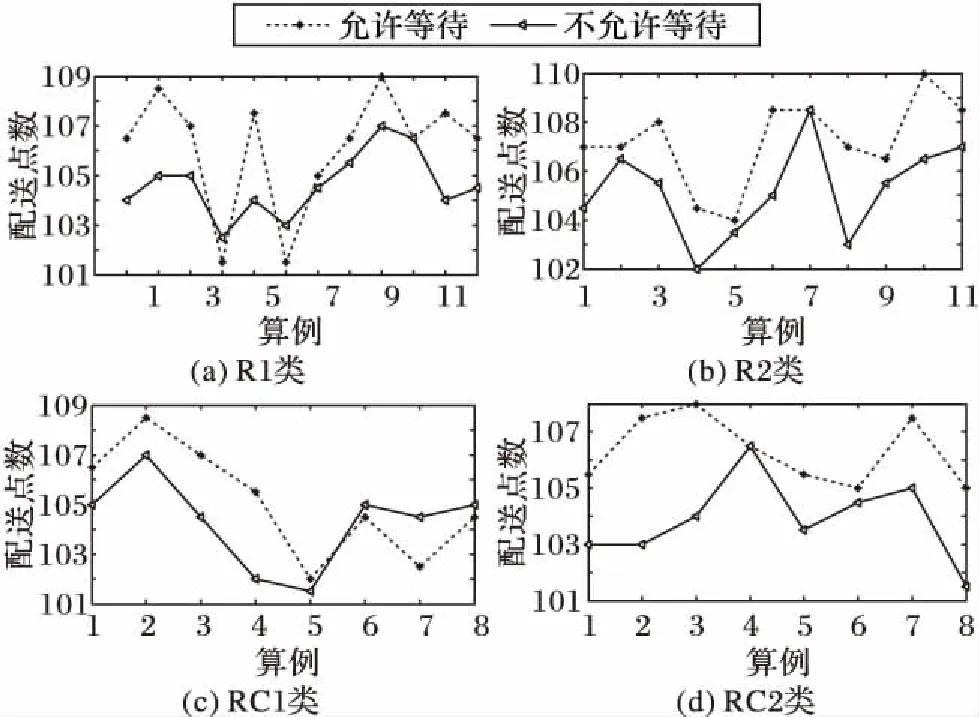
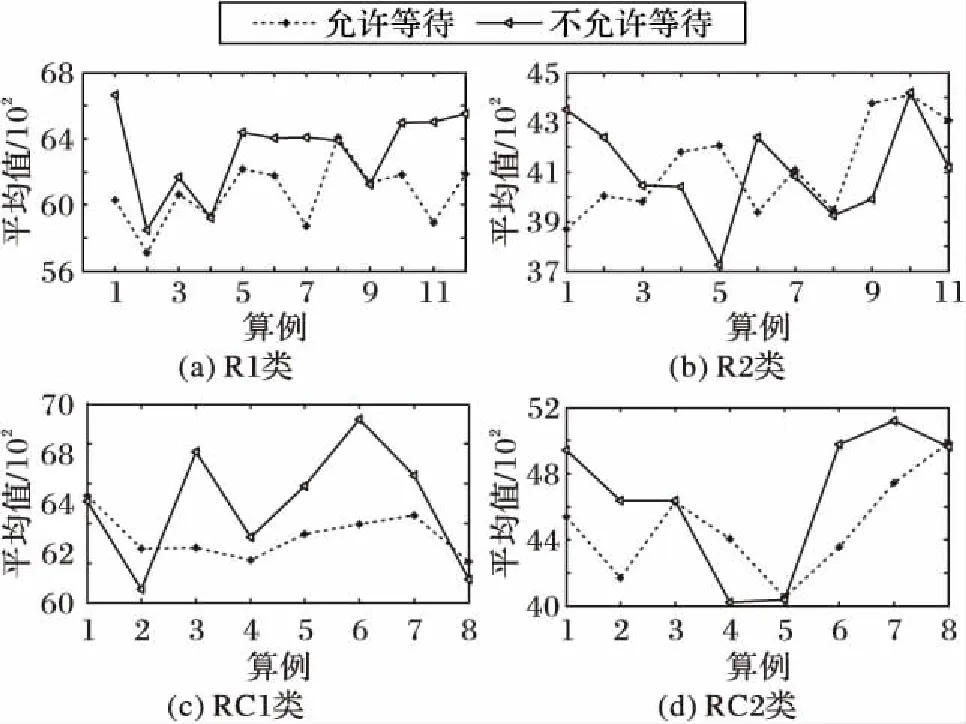
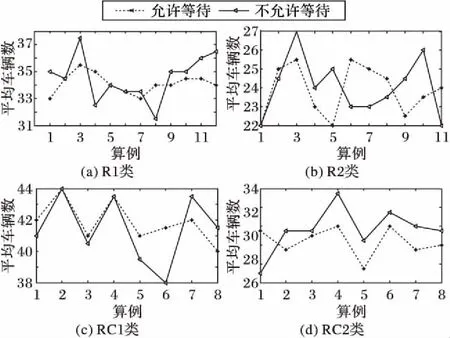
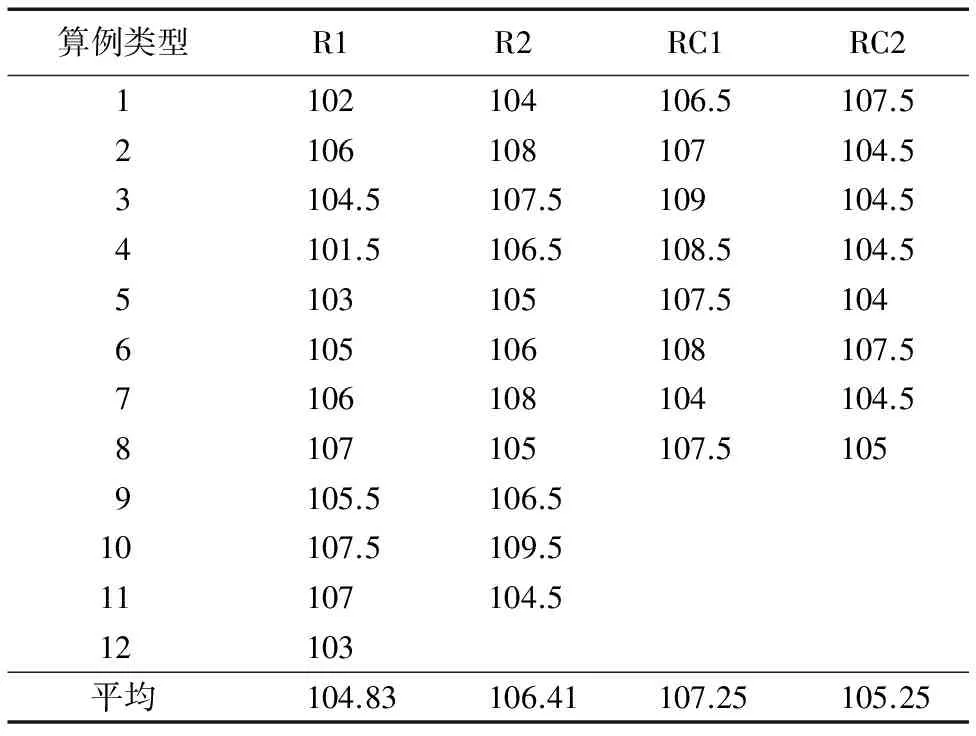
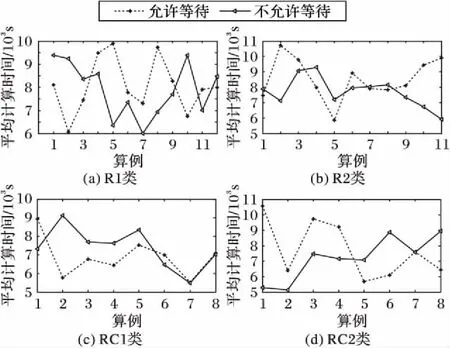
本文采用Ho等[6]提出的调整方式对实验算例进行调整。其中：节点(包括车场和需求点)的位置、车容量、时间窗和服务时间与Solomon[33]的例子相同。在此基础上，考虑对各个需求点的平均需求进行调整，将平均需求调整到区间[vQ,uQ]，其中，v和u均为(0，1]区间的数，且v

(9)

Silva等[34]考虑不同的组合值：[0.01，0.1]，[0.1，0.3]，[0.1，0.5]，[0.1，0.9]，[0.3，0.7]，[0.7，0.9]，并证实平均需求量较大的算例分割现象较明显。综合现有结果，本文考虑[v,u]取值为[0.1，0.9]和[0.3，0.7]的情况，所有调整的需求均取整。

3.2　算法参数

本文算法在Marinakis[31]算法的基础上进行设计，故算法参数参考Marinakis[31]中的参数取值如表2所示。

3.3　结果分析

在每个算例上分别针对[0.1,0.9]和[0.3,0.7]运行10次，选取两种情况下的最优解，然后使用这两个最优解的平均值进行分析。由于尚未发现可直接与本文结果进行比较的成果，本文考虑否允许等待和是否允许分批配送两种角度对结果进行分析。

表2　实验中算法的参数选取Tab. 2　Experimental parameters selection of the algorithm

3.3.1是否允许等待的情况比较

不允许等待的情况同一般情况下的软时间窗问题相同，不考虑等待时间，只考虑提前服务和延迟服务的惩罚费用。

1)总费用。是否允许等待两种情况下的总费用对比如图1所示。

图1　总费用在是否允许等待情况下的比较Fig. 1　Comparison of all-in cost for allowing waiting or not

从图1可以看出，四类算例中绝大部分算例允许等待时总费用高于不允许等待时的总费用，平均高出3%左右。从计算结果看，产生此类现象的原因主要是由于考虑等待时间造成车辆服务时间延长，从而导致平均使用车辆数增加,具体如图2所示。从图2可以看出，超过70%以上的算例使用车辆数在考虑等待的情况下高于不考虑等待的情况，由于考虑等待而导致的车辆数平均增加0.62。但是，等待在实际配送过程中是普遍存在的，因此在实际配送运营中应尽量减少等待时间，以提升配送人员效率，提升服务效率。

2)行驶费用和惩罚费用。行驶费用是指不与时间相关的费用，包括车辆使用费用和车辆行驶距离产生的费用；惩罚费用是指与时间相关的费用，包括提前服务和延迟服务产生的惩罚费用。

如图3、图4所示，考虑等待时间造成行驶费用占总费用的比例比不考虑等待时间时比例略微降低，平均降低约0.6%，主要由于行驶费用变化不大(平均增加约68.30)，其增加的幅度低于总费用增加的幅度；同时惩罚费用占总费用的比例降低明显，平均降低约9.65%，绝对值上平均约降低467。从此现象可以看出，等待时间对惩罚费用影响较大，同时等待时间产生的费用部分由惩罚费用转化而来。

图2　车辆数在是否允许等待情况下的比较Fig. 2　Comparison of number of vehicles for allowing waiting or not

图3　行驶费用占总费用的比在是否允许等待情况下的比较Fig. 3　Comparison of ratio of travel cost in all-in cost for allowing waiting or not

图4　惩罚费用占总费用的比在是否允许等待情况下的比较Fig. 4　Comparison of ratio of penalty cost in all-in cost for allowing waiting or not

3)考虑等待时间时更倾向于分批配送。如图5所示，从最优解中最终配送点数量来看，80%以上的算例考虑等待时间时多于不考虑等待时间的情况，平均多约2.8个；考虑等待时间更倾向于分批配送。

3.3.2是否允许分批的情况比较

1)总费用对比。如图6所示，总体来看，允许分批配送时比不允许分批配送时总费用有所降低。所有测试算例中，约61.5%的算例总费用低于不允许分批配送，所有算例总费用平均降低约2%。

图5　配送点数量在是否允许等待情况下的比较Fig. 5　Comparison of number of delivery customers for allowing waiting or not

图6　总费用在是否允许分批配送情况下的对比Fig. 6　Comparison of all-in cost for allowing split or not

2)车辆数对比。如图7所示，总体来看，是否允许分批配送对最优解中车辆数的影响不具有一般规律，特别在R1、R2类算例中。在RC1类算例中，不允许分批配送时车辆数总体少于允许分批配送；而在RC2类算例中，不允许分批配送时车辆数则多于允许分批配送，此时分批配送将为最优解带来更显著的节约。将所有算例数据汇总来看，允许分批配送时使用的车辆数比不允许分批配送时使用的车辆数平均少约0.6。

3)配送点数。如表3所示，四类算例平均配送点数达105.9，分割点比例达到5.9%，测算过程中，80%以上的算例最优解中均产生分批配送的需求点，允许分批在较大规模算例中能起到较好作用。

4)计算时间对比。如图8所示，总体来看，是否允许分批配送对计算时间的影响不具有一般规律。所有算例允许分批配送比不允许分批配送时的平均计算时间多约300 s。

图7　车辆数在是否允许分批配送情况下的对比Fig. 7　Comparison of number of vehicles for allowing split or not

表3　四类算例平均配送点数Tab. 3　Average number of delivery customers for four types of instances

图8　平均计算时间在是否允许分批配送情况下的对比Fig. 8　Comparison of average computing time for allowing split or not

5)等待费用占总费用的比例。如图9所示,总体来看，是否允许分批配送对等待费用占总费用的比例影响较小。所有算例允许分批配送比不允许分批配送的占比约降低0.78%，允许分批配送在部分算例中能有效降低车辆等待时间，特别在R2类算例中表现比较明显。

图9　等待费用占总费用的比例在是否允许分批配送情况下的对比Fig. 9　Comparison of ratio of waiting cost in all-in cost for allowing split or not

4　结语

本文在软时间窗下考虑等待时间，建立带修正的随机规划模型，并设计改进的PSO算法进行求解。算法结合三类不同的拓扑，使用路径重连算法有效解决了粒子位置向量在连续空间和离散空间转换造成的信息丢失问题，并采用自适应选择解决了分批配送引起的向量长度不一致问题。

通过对调整的Solomon算例进行测试，算法能有效求解本文提出的问题。考虑等待时间将造成总费用平均增加约3%，使用的车辆数平均增加0.62。惩罚费用占总费用的比例平均降低约9.65%，考虑等待时间对惩罚费用影响较大，等待时间产生的费用部分由惩罚费用转化而来。同时考虑等待时间的情况也更倾向于分批配送，最终配送点数平均多约2.8。

分批配送能有效降低总费用和使用车辆数，分别平均降低约2%和0.6辆;而且允许分批配送在部分算例中能有效降低车辆等待时间，特别是在R2类算例中表现比较明显，所有等待时间平均约降低0.78%。

进一步的研究集中在两个方面:1)设计更高效的基于种群的进化算法求解随机分批配送问题，比如萤火虫群算法等；设计动态求解或精确求解算法解决行驶时间随机车辆路径问题等。2)寻求合理的方法对等待时间分布进行研究，更深入、精确地分析等待时间在配送中的影响；将城市交通流量、交通信号控制等与车辆路径问题相结合，考虑更接近现实情况、更复杂的动态车辆路径问题。

参考文献:

[1]EHMKE J F, CAMPBELL A M, URBAN T L. Ensuring service levels in routing problems with time windows and stochastic travel times [J]. European Journal of Operational Research, 2015, 240(2): 539-550.

[2]LI X, TIAN P, LEUNG S C H. Vehicle routing problems with time windows and stochastic travel and service times: models and algorithm [J]. International Journal of Production Economics, 2010, 125(1): 137-145.

[3]DROR M, TRUDEAU P. Savings by split delivery routing [J]. Transportation Science, 1989, 23(2): 141-145.

[4]ARCHETTI C, SPERANZA M G. Vehicle routing problems with split deliveries [J]. International Transactions in Operational Research, 2012, 19(1/2): 3-22.

[5]FRIZZELL P W, GIFFIN J W. The split delivery vehicle scheduling problem with time windows and grid network distances [J]. Computers & Operations Research, 1995, 22(6): 655-667.

[6]HO S C, HAUGLAND D. A Tabu search heuristic for the vehicle routing problem with time windows and split deliveries [J]. Computers & Operations Research, 2004, 31(12): 1947-1964.

[7]BELFIORE P, YOSHIDA YOSHIZAKI H T. Scatter search for a real-life heterogeneous fleet vehicle routing problem with time windows and split deliveries in Brazil [J]. European Journal of Operational Research, 2009, 199(3): 750-758.

[8]MCNABB M E. Exploring heuristics for the vehicle routing problem with split deliveries and time windows [D]. Ohio: Air University, Department of the Air Force, Wright-Patterson Air Force Base, 2014: 29-63.

[9]SALANI M, VACCA I. Branch and price for the vehicle routing problem with discrete split deliveries and time windows [J]. European Journal of Operational Research, 2011, 213(3): 470-477.

[10]DESAULNIERS G. Branch-and-price-and-cut for the split-delivery vehicle routing problem with time windows [J]. Operations Research, 2010,58(1): 179-192.

[11]ARCHETTI C, BOUCHARD M, DESAULNIERS G. Enhanced branch and price and cut for vehicle routing with split deliveries and time windows [J]. Transportation Science, 2011, 45(3): 285-298.

[12]BOUZAIENE-AYARI B, DROR M, LAPORTE G. Vehicle routing with stochastic demand and split deliveries [J]. Discrete Applied Mathematics, 1994, 50(3): 239-254.

[13]LEI H, LAPORTE G, GUO B. The vehicle routing problem with stochastic demands and split deliveries [J]. INFOR: Information Systems & Operational Research, 2012, 50(2): 59-71.

[14]ZHANG J, LAM W H K, CHEN B Y. A stochastic vehicle routing problem with travel time uncertainty: trade-off between cost and customer service [J]. Networks and Spatial Economics, 2013, 13(4): 471-496.

[15]杨信丰,杨庆丰.随机车辆路径问题的模型及其算法[J].交通运输系统工程与信息,2006,6(4):75-80. (YANG X F, YANG Q F. Model and algorithm of vehicle routing problem with stochastic travel time [J]. Journal of Transponation systems Engineering and Information Technology, 2006, 6(4): 75-80.)

[16]李锋,魏莹.求解随机旅行时间的C-VRP问题的混合遗传算法[J].系统管理学报,2014,23(6):819-825. (LI F, WEI Y. Hybrid genetic algorithm for capacitated vehicle routing problem with stochastic travel time [J]. Journal of Systems & Management, 2014, 23(6): 819-825.)

[17]王征,胡祥培,王旭坪.行驶时间延迟下配送车辆调度的干扰管理模型与算法[J].系统工程理论与实践,2013,33(2):378-387. (WANG Z, HU X P, WANG X P. Disruption management model and algorithm for distribution vehicle scheduling problems under accidental travel time delay [J]. Systems Engineering — Theory & Practice, 2013, 33(2): 378-387.)

[18]李妍峰,高自友,李军.基于实时交通信息的城市动态网络车辆路径优化问题[J].系统工程理论与实践,2013,33(7):1813-1819. (LI Y F, GAO Z Y, LI J. Vehicle routing problem in dynamic urban network with real-time traffic information[J]. Systems Engineering — Theory & Practice, 2013, 33(7): 1813-1819.)

[19]ANDO N, TANIGUCHI E. Travel time reliability in vehicle routing and scheduling with time windows [J]. Networks and Spatial Economics, 2006, 6(3/4): 293-311.

[20]RUSSELL R A, URBAN T L. Vehicle routing with soft time windows and erlang travel times [J]. The Journal of the Operational Research Society, 2008, 59(9): 1220-1228.

[21]李相勇,田澎.带时间窗和随机时间车辆路径问题:模型和算法[J].系统工程理论与实践,2009,29(8):81-90. (LI X Y, TIAN P. Vehicle routing problems with time windows and stochastic times: models & algorithm [J]. Systems Engineering — Theory & Practice, 2009, 29(8): 81-90.)

[24]EHMKE J F, CAMPBELL A M, URBAN T L. Ensuring service levels in routing problems with time windows and stochastic travel times [J]. European Journal of Operational Research, 2015, 240(2): 539-550.

[25]MARINAKIS Y, MARINAKI M, DOUNIAS G. A hybrid particle swarm optimization algorithm for the vehicle routing problem [J]. Engineering Applications of Artificial Intelligence, 2010, 23(4): 463-472.

[26]KECHAGIOPOULOS P N, BELIGIANNIS G N. Solving the urban transit routing problem using a particle swarm optimization based algorithm [J]. Applied Soft Computing, 2014, 21: 654-676.

[27]AI T J, KACHITVICHYANUKUL V. Particle swarm optimization and two solution representations for solving the capacitated vehicle routing problem [J]. Computers & Industrial Engineering, 2009, 56(1): 380-387.

[28]CHEN M-C, HSIAO Y-H, HIMADEEP REDDY R, et al. The self-learning particle swarm optimization approach for routing pickup and delivery of multiple products with material handling in multiple cross-docks [J]. Transportation Research Part E: Logistics and Transportation Review, 2016, 91: 208-226.

[29]NOROUZI N, SADEGH-AMALNICK M, ALINAGHIYAN M. Evaluating of the particle swarm optimization in a periodic vehicle routing problem [J]. Measurement, 2015, 62: 162-169.

[30]BOUDIA M, PRINS C, REGHIOUI M. An effective memetic algorithm with population management for the split delivery vehicle routing problem [C]// HM’07: Proceedings of the 4th International Conference on Hybrid Metaheuristics, LNCS 4771. Berlin: Springer, 2007: 16-30.

[31]MARINAKIS Y. An improved particle swarm optimization algorithm for the capacitated location routing problem and for the location routing problem with stochastic demands [J]. Applied Soft Computing, 2015, 37: 680-701.

[32]MARINAKIS Y, MARINAKI M. Combinatorial expanding neighborhood topology particle swarm optimization for the vehicle routing problem with stochastic demands [C]// GECCO ’13: Proceedings of the 2013 Conference on Genetic and Evolutionary Computation. New York: ACM, 2013: 49-56.

[33]SOLOMON M M. Algorithms for the vehicle routing and scheduling problems with time window constraint [J]. Operations Research, 1987, 35(2): 254-265.

[34]SILVA M M, SUBRAMANIAN A, OCHI L S. An iterated local search heuristic for the split delivery vehicle routing problem [J]. Computers & Operations Research, 2015, 53: 234-249.