基于监督下降方法的左心室超声图像分割

魏雨汐，伍岳庆，陶　攀,2，姚　宇

(1.中国科学院 成都计算机应用研究所，成都 610041；　2.中国科学院大学，北京 100049)(*通信作者电子邮箱weiyuxi272@163.com)

0　引言

在医学超声图中，经食道的超声心动检测是常见的超声探测方式之一，也是人体左心室功能评价的重要参考[1]。医学图像分割是医学图像处理与分析领域复杂而关键的步骤，其目的是分割出医学图像中具有某些特殊含义的部分，并提取相关特征，为临床诊疗和病理学研究提供可靠的依据，辅助医生作出更为准确的诊断[2]。

近年来，研究者们采用各类图像分割算法应用于医学图像处理领域，如：Pieciak[3]基于主动轮廓模型(Active Contour Model, ACM)方法[4]对核磁共振成像(Magnetic Resonance Imaging, MRI)的左心室进行分割；Hajiaghayi等[5]利用改进的ACM方法将心脏MRI数据重建为3D模型，提出了一种三维分割的算法；O’Brien等[6]基于主动形状模型(Active Shape Model, ASM)[7]在3D图像中对左心室进行多轮廓分割；刘金清等[8]基于主动表观模型(Active Appearance Model, AAM)[9-10]方法对膀胱MRI医学图像进行分割。

由于超声心动图的复杂性和多变性，其分割过程需利用图像中特征点位置的迭代变换，最终达到对目标区域进行轮廓提取的目的，其实质上可视为特征点定位的问题。而特征点的定位过程可以理解为非线性最小二乘近似问题[11]。传统的基于统计分布的ASM方法或AAM方法在建立形状模型或表观模型时使用的牛顿法或拟牛顿法在算法中计算代价较高，为此文献[12]提出了一种监督下降方法(Supervised Descent Method， SDM)来替代搜索过程中雅克比矩阵和海森矩阵的复杂计算，用于解决计算机视觉中的非线性最小二乘问题，在图像的特征点定位上取得了很好的效果。

SDM的目标函数定义为最优化两个特征向量的相似程度，传统的方法一般采用两个特征向量的欧氏距离来作为特征点之间的相似性判定度量。而文献[13]中已经通过实验证明了基于巴氏系数(Bhattacharyya coefficient)的直方图相似性判定相比传统的欧氏距离的准确性优势。同时，在超声图像处理领域，文献[14]提出了一种基于巴氏系数的主动轮廓模型图像分割方法，提升了原方法的鲁棒性。本文采用一种基于巴氏系数改进的尺度不变特征变换(Bhattacharyya-Scale Invariant Feature Transform, B-SIFT)特征的SDM，并结合多尺度图像金字塔建立了心内膜与心外膜的联合形状模型，对左心室区域进行准确分割提取，取得了良好效果。

1　基于监督下降的左心室超声图像分割方法

在特征点定位过程中，传统的基于表观模型的AAM算法的优化目标可定义为一个非线性最小二乘问题：

(1)

其中：x=[x1,y1,x2,y2,…,xN,yN]T∈R2N×1为图像d(x)中N个特征点组成的形状向量；p为变换参数；f(x,p)表示对x进行相应的仿射变换[16]和非刚性变换[17]；d(f(x,p))表示变换后的图像；Ua和ca为表观模型和表观参数。

若用传统的牛顿法解决上述最优化问题，在每一步的迭代中都要计算相应的海森矩阵与雅克比矩阵，那么将花费巨大的计算代价[18]。而SDM则无需进行上述复杂的计算，也无需建立表观模型，仅需利用提取到的局部特征从训练数据学习一组梯度下降方向，并应用到测试集图像上。其核心过程主要涉及以下步骤：

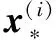
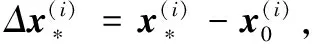
3)计算对应特征点新的位置，更新位置迭代方向及其对应的偏差项。

4)重复2)、3)直至收敛，最终得到方向序列{Rk}和偏差项序列{bk}。

5)在测试过程中，将训练得到的{Rk}和{bk}作用于测试集图像的初始位置，得到最终的特征点定位结果。

1.1　监督下降方法(SDM)

SDM的优化目标和AAM有所不同，定义为特征函数之间的最优化问题，其目标为最优化式(2)所示的非线性最小二乘问题：

f(x0+Δx)=‖h(d(x0+Δx))-h(d(x*))‖2

(2)

其中:d∈Rm×1表示一个具有m个像素点的图像；d(x)∈Rp×1表示图d中的p个特征点组成的形状向量；h为特征提取函数，h(d(x))表示在图像上对p个特征点的局部特征进行提取；向量x*表示p个特征点的最佳位置，且在训练阶段是已知的；x0表示初始形状位置，通常由训练样本的平均形状表示。左心室特征点优化的目标即为当前的特征点位置找到一个趋近于最优值的位置偏移Δx。

为求解式(2)中的Δx，将其进行二阶泰勒展开，得：

(3)

令φk=h(d(xk))，在式(3)对Δx求导并令其为0得到Δx的第一个更新：

Δx1=-H(x0)-1Jf(x0)=

-2H(x0)-1Jh(x0)T(φ0-φ*)

(4)

其中：H(x0)为函数f在x0处的海森矩阵；Jf(x0)为函数f在x0处的雅克比矩阵。在SDM中，可通过监督学习找到表示迭代方向的R0和表示偏差项的b0替代式(4)中的-2H(x0)-1Jh(x0)T与2H(x0)-1Jh(x0)Tφ*，由此便可构造出Δx1的求解式如式(5)所示：

Δx1=R0φ0+b0

(5)

所以最初最优化问题转化为求解R0和b0，其求解方式由式(6)给出，上标i表示训练样本中的第i幅图像：

(6)

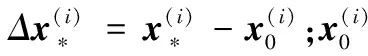
而对于非线性的最小二乘问题，需要多次迭代才能得到最优结果。对于每一次迭代都会产生一个Rk和bk，便组成一个方向序列{Rk}和一个偏差项序列{bk}。一般地，对于第k次迭代，结合前一步得到的Rk-1和bk-1，有：

xk=xk-1+Rk-1φk-1+bk-1

(7)

(8)

在测试阶段，给定待测试图像的初始位置x0，将训练得到的{Rk}和{bk}作用于x0上，以得到最终的真实位置估计。图1简要描述了SDM从初始位置到最佳位置的大致过程。

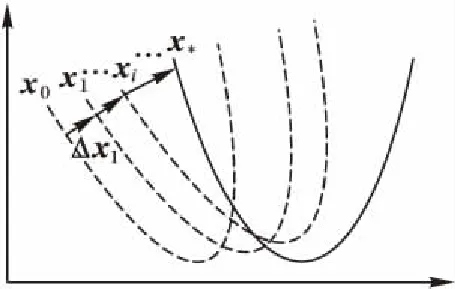
图1　SDM收敛过程Fig. 1　Convergence process of SDM

由式(2)不难看出，SDM的核心在于最优化两个特征向量的欧氏距离，所以特征提取函数的选取对算法迭代过程中{Rk}和{bk}的生成有直接影响。

1.2　基于SDM的改进算法

由于图像特征提取函数的选取会影响SDM的最终分割效果，因此对左心室超声图像准确分割的实现有着重要意义。由于受光照程度不同、心内组织密度各异等客观影响，传统SDM采用的SIFT特征提取函数在左心室轮廓定位上取得的效果欠佳。为弱化上述客观影响，本文采用B-SIFT特征，其效果比传统的SIFT特征要好；同时，在模型中引入了多尺度图像金字塔模型来进一步提升最终左心室轮廓分割效果。

1.2.1基于SIFT特征的优化特征B-SIFT

SIFT特征是一种局部特征检测方法，广泛应用于多类计算机视觉领域。其优点在于：具有尺度、旋转不变性，对噪声、图像亮度变换有很好的抵抗力，所蕴含的局部特征信息量丰富等。

对于SIFT特征向量的提取，在初始形状向量x0中的每一个特征点周围建立16×16的像素框，计算其中每一个像素的梯度；然后每4×4的像素上计算8个方向的梯度方向直方图如图2(a)所示；绘制每个梯度方向的累加值，如图2(b)所示。于是便得到4×4×8=128维的SIFT特征向量(又称描述子)。

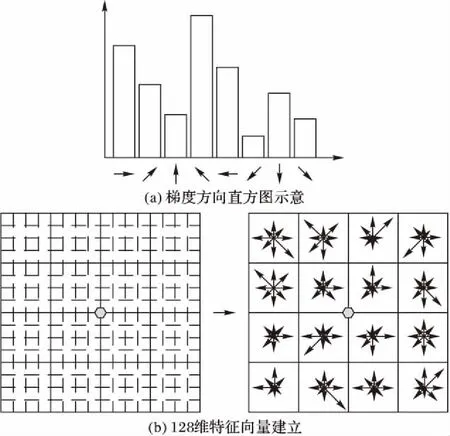
图2　SIFT特征建立Fig. 2　Construction of SIFT features

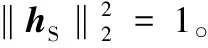
本文采用基于巴氏系数的B-SIFT特征替代原SIFT特征以辅助特征点定位，取得了较好的效果。其构造方法如下：

对于两个n维单位特征向量x、y，定义x与y的巴氏系数为：

(9)

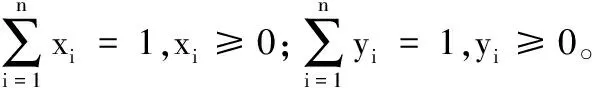
(10)

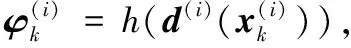
(11)

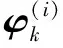
1.2.2多尺度图像金字塔模型建立

在左心室超声图的探测过程中，受左心室的形状、大小、心尖朝向等客观因素的影响，在对训练集或测试集中的图像统一归一化后，可能会造成局部纹理信息丢失，影响最终结果的准确性。于是，本文采用了基于多尺度图像金字塔模型的方式，将训练集中的图像归一至多个分辨率上，在低分辨率图像上进行步长较大的迭代，在高分辨率图像上进行步长较小的迭代，使特征点更为精确地贴近真实值。分辨率从上至下依次递增，完成每一层的特征点匹配后，转至下一层。本文采用的四层金字塔结构如图3所示。

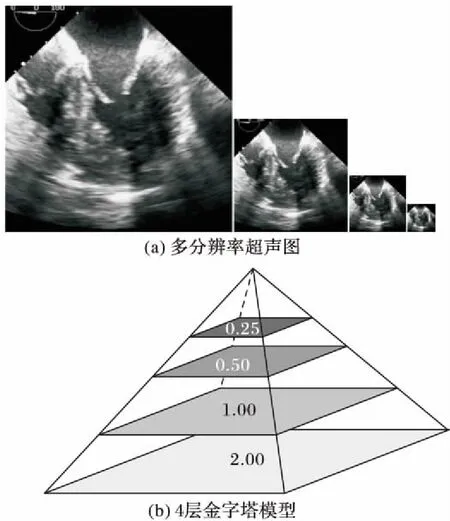
图3　多分辨率金字塔模型Fig. 3　Multi-resolution pyramid model

2　实验及其结果分析

本文实验数据来自于华西医院专家标注的心动周期不同阶段的106张超声心动图，来自于25位不同的患者，提取其中81张作为训练集，25张作为测试集。在特征点标注方面，选取左心室心内膜和心外膜作为参考轮廓，分别标注17个特征点，其中0～16号特征点为心外膜，17到33号特征点为心内膜，如图4所示。

图4　手工标注的特征点Fig. 4　Mannually labeled feature points

实验将本文采用的方法对测试集的经食道的超声心动图像进行了特征点定位操作，分割出心内膜与心外膜的轮廓，并与传统的SDM进行了对比，描述如下。

2.1　B-SIFT与SIFT实验效果对比

在同时基于4层多尺度金字塔模型的基础上，从上至下缩放尺度依次设为0.25、 0.5、 1.0和2.0，每一层迭代次数为2，特征提取函数分别设为B-SIFT和SIFT，实验结果如图5所示，图5(a)为采用SIFT特征的特征点定位轮廓，图5(b)为采用B-SIFT特征的特征点定位轮廓。其中黑色特征点为真实值位置，白色特征点为实验结果位置。观察两者的心室轮廓的高曲率区域，发现基于B-SIFT特征的实验结果比SIFT更加接近真实值。

图5　利用SIFT与B-SIFT特征进行特征点定位的结果对比Fig. 5　Comparison of feature point location results using B-SIFT and SIFT features

2.2　构建多尺度图像金字塔后改进效果

本实验构建了4层多分辨率金字塔迭代模型，在采用相同特征提取函数的情况下，其相对于没有金字塔结构的SDM模型在精准度上有较大提升。选取测试集中的一张图像作演示：图6(a)为初始化特征点定位x0；图6(b)为非金字塔结构的监督下降方法SDM的分割效果，其只在单一尺度(scale=1.0)上进行迭代；图6(c)是基于4层金字塔模型的特征点定位效果。其中黑色特征点为真实值位置，白色特征点为实验迭代结束位置。可以看出：基于多尺度图像金字塔模型的特征点定位更接近真实轮廓。

综上所述，结合多尺度金字塔模型和B-SIFT特征提取函数的左心室轮廓分割方法在精准度上要优于传统的SDM特征点标注方法。本文方法与传统SDM的累计误差分布图如图7所示，其中横坐标为测试集序列号，纵坐标为其误差累计。从图7可以看出，基于B-SIFT特征提取函数的方法效果优于传统SDM。

图6　多分辨率金字塔优化效果Fig. 6　Optimization result of multi-resolution pyramid

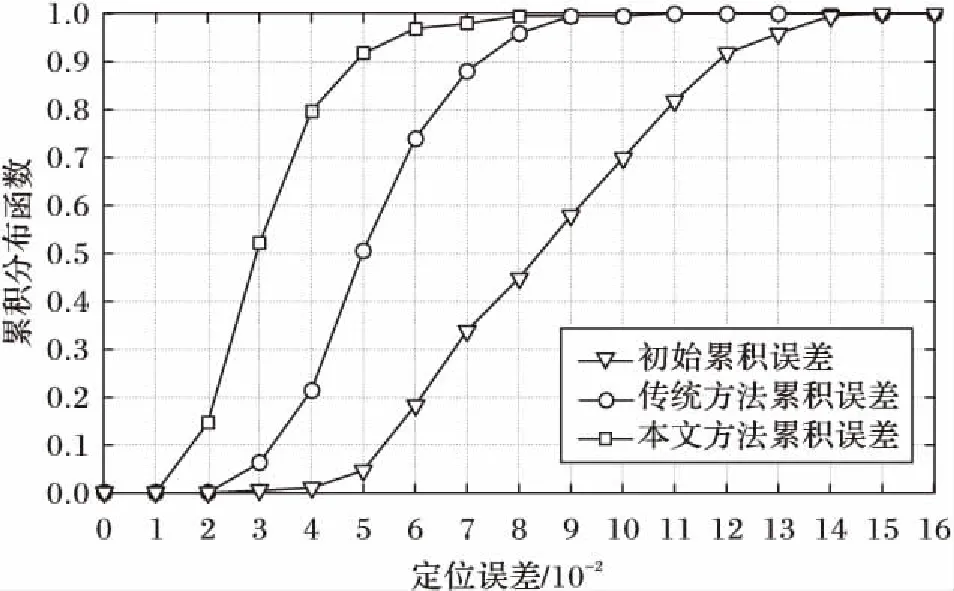
图7　传统SDM和本文方法的累计误差分布对比Fig. 7　Cumulative error distribution comparison of the traditional SDM and the proposed method

将传统SDM与本文方法作用于测试集中，得到的平均误差结果如表1所示。可以看出，基于B-SIFT特征及多尺度图像金字塔的分割方法将平均误差从0.055 73降低至0.029 30，准确度提升了47.43%。

表1　传统SDM与本文方法的平均误差对比Tab. 1　Average error comparison of the traditional SDM and the proposed method

3　结语

本文基于SDM对经食道超声心动图中左心室轮廓进行了分割，针对传统方法在单一尺度上定位的精确性问题，建立了4层金字塔特征点定位搜索模型，并结合基于巴氏系数改进的尺度不变特征变换(B-SIFT)特征提取函数，进一步提高了算法的准确性,使最终的特征点定位输出更加接近真实轮廓。在下一步研究中，计划建立左心室特征点标注图像库，增加标注图像的样本数量，利用局部特征描述子匹配，将算法应用于动态超声视频追踪上。

参考文献:

[1]朱文玲.超声心动图评价左心室功能[J].中国心血管杂志,2008,13(4):241-243. (ZHU W L. Evaluation of left ventricular function by echocardiography[J]. Chinese Journal of Cardiovascular Medicine, 2008, 13(4):241-243.)

[2]黄文博,燕杨,王云吉.医学图像分割方法综述[J].长春师范大学学报(自然科学版),2013,32(2):22-25. (WANG W B, YAN Y, WANG Y J. Survey of medical image segmentation methods [J]. Journal of Changchun Normal University (Natural Science), 2013, 32(2): 22-25.)

[3]PIECIAK T. Segmentation of the left ventricle using active contour method with gradient vector flow forces in short-axis MRI [M]// Information Technologies in Biomedicine, LNCS 7339. Berlin: Springer, 2012: 24-35.

[4]DAVATZIKOS C, PRINCE J L. An active contour model for mapping the cortex [J]. IEEE Transactions on Medical Imaging, 1995, 14(1): 65-80.

[5]HAJIAGHAYI M, GROVES E M, JAFARKHANI H, et al. A 3-D active contour method for automated segmentation of the left ventricle from magnetic resonance images [J]. IEEE Transactions on Biomedical Engineering, 2016, 64(1): 134-144.

[6]O’BRIEN S, GHITA O, WHELAN P F. Segmenting the left ventricle in 3D using a coupled ASM and a learned non-rigid spatial model [C/OL]// 3D Segmentation in the Clinic: A Grand Challenge III [Workshop], MICCAI 2009: Proceedings of the 12th International Conference on Medical Image Computing and Computer Assisted Intervention [2017- 03- 16]. http://doras.dcu.ie/18626/1/whelan_2009_52.pdf.

[7]COOTES T F, TAYLOR C J, COOPER D H, et al. Active shape models—their training and application [J]. Computer Vision and Image Understanding, 1995, 61(1): 38-59.

[8]刘金清,吴庆祥.一种AAM模型的MRI医学图像分割算法[J].电子测量与仪器学报,2013,27(3):236-240. (LIU J Q, WU Q X. Algorithm of AAM model for MRI medical image segmentation [J]. Journal of Electronic Measurement and Instrument, 2013, 27(3): 236-240.)

[9]COOTES T F, EDWARDS G J, TAYLOR C J, et al. Active appearance models [J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2001, 23(6): 681-685.

[10]MATTHEWS I, BAKER S. Active appearance models revisited [J]. International Journal of Computer Vision, 2004, 60(2): 135-164.

[11]XIONG X. Supervised descent method [C]// Proceedings of the 2015 IEEE Computer Vision and Pattern Recognition. Piscataway, NJ: IEEE, 2015: 2664-2673.

[12]XIONG X, DE LA TORRE F. Supervised descent method and its applications to face alignment [C]// CVPR 2013: Proceedings of the 2013 IEEE Conference on Computer Vision and Pattern Recognition. Washington, DC: IEEE Computer Society, 2013: 532-539.

[13]ARANDJELOVIC R. Three things everyone should know to improve object retrieval [C]// CVPR 2012: Proceedings of the 2012 IEEE Conference on Computer Vision and Pattern Recognition. Washington, DC: IEEE Computer Society, 2012: 2911-2918.

[14]YUAN J. Active contour driven by region-scalable fitting and local Bhattacharyya distance energies for ultrasound image segmentation [J]. IET Image Processing, 2013, 6(8): 1075-1083.

[15]LOWE D G. Object recognition from local scale-invariant features [C]// ICCV ’99： Proceedings of the Seventh IEEE International Conference on Computer Vision. Washington, DC: IEEE Computer Society, 2002, 2: 1150.

[16]KENDALL R A, DUNNING H T, Jr., HARRISON R J. Electron affinities of the first-row atoms revisited. Systematic basis sets and wave functions [J]. Journal of Chemical Physics, 1992, 96: 6796-6806.

[17]谭志国,刘滕冲,孙即祥,等.一种非刚性医学图像点匹配方法[J].武汉大学学报(理学版),2007,53(6):759-764. (TAN Z G, LIU T C, SUN J X, et al. A non-rigid medical image point matching method [J]. Journal of Wuhan University (Natural Science Edition), 2007, 53(6): 759-764.)

[18]邓梁.基于ASM与AAM的人脸特征定位与匹配算法研究[D].长沙:中南大学,2009:15-20. (DENG L. Research on face feature positioning and matching algorithm based on ASM and AAM [D]. Changsha: Central South University, 2009: 15-20.)