基于先验约束和统计的图像修复算法

曹大命，翟东海，孟红月，李梦雪，冯　炎

(1.西南交通大学 信息科学与技术学院，成都 610031；　2.西藏大学 工学院，拉萨 850000)(*通信作者电子邮箱1120490970@qq.com)

0　引言

图像修复是目前数字图像处理领域的研究热点，它是一个病态问题，即利用图像完好区域的信息来推测修复图像破损区域的信息，目的在于恢复破损图像的完整性，使其符合视觉连通性的要求。图像修复技术已经被广泛用于旧照片修复、影视特效制作、文物保护等多个领域[1]。目前关于图像修复研究方法主要分为三类：基于偏微分方程(Partial Differential Equation, PDE)的图像修复算法、基于稀疏的图像修复算法和基于样本的图像修复算法[2]。

基于PDE的图像修复算法通常是从已知区域向破损区域扩散图像信息，该方法常用来修复图像破损区域较小的非纹理图像，对于大破损区域且含有几何结构的图像会产生错误修复和模糊现象[2]。其经典的代表算法有：Bertalmio等[3]提出的一种沿着图像的等照度线信息从破损区域边缘不断扩散信息到破损区域内部的修复方法；Chan等[4]提出的利用全变分(Total Variation, TV)和各项异向扩散来修复局部非纹理图像的全变分修复模型。

基于稀疏的图像修复算法主要是通过将图像表示成一系列变换的稀疏组合，破损区域的像素可以通过自适应更新稀疏表示被填充，在修复过程中该类方法也会产生模糊现象。该类方法中的代表算法有：Elad等[5]使用MCA(Morphological Component Analysis)将图像分解成纹理层和结构层，每层通过不同的字典稀疏表示出来，从而实现纹理和结构的同时修复； Yu等[6]提出的将结构稀疏性引入图像修复过程的修复方法。

基于样本的图像修复方法可细分为基于匹配(match)的图像修复算法和基于图(graph)的图像修复算法[7]。基于匹配的图像修复算法通常利用设置优先权查找最佳样本块，再用最佳样本块填充破损区域，其经典代表算法有：Efrosa等[8]提出的纹理合成的方法和Criminisi等[9]提出的基于最佳样本的图像修复算法;Wexler等[10]提出的定义一个全局代价函数使得被填充区域的目标块尽可能和完好区域的样本块相似从而完成图像修复过程的图像修复方法。但此类算法具有贪婪性，对算法初始化和所采用的优化方法较敏感。基于图的图像修复算法[11-13]通常利用可尔可夫随机场(Markov Random Field, MRF)模型重排样本块的位置来完成图像修复过程，其典型代表算法有： Komodakis等[11]提出的先验置信传播(priority Belief Propagation,priority-BP)算法， Pritch等[12]提出的shift-map算法等。但此类方法计算量比较大。

基于以上研究基础，本文提出了基于先验约束和统计的图像修复算法，该算法主要通过约束初始化和引导搜索两个步骤来达到提高匹配精度的目的；在图像修复阶段利用相似块的偏移值具有稀疏性这一图像统计特性[7]，采用二维直方图统计出主要偏移值，来减少样本标签的数量，从而提高算法的时效性。

1　算法概述

基于图(graph-based)的图像修复算法[7]通过优化像MRF那样的基于图的模型，向未知像素点/块分配一个偏移量(offset)，未知像素点/块利用这个偏移量找到其最优匹配块的相对位置，并从中复制最优匹配块的内容到未知像素点/块来完成图像的修复过程。如何获得最优的图像的偏移映射图(shift-map)是评价此类修复算法优劣的关键。由引言可知，该类算法普遍存在算法计算量大、时效性较差的问题。Barnes等[13]提出的PatchMatch算法和He等[7]提出的相似块统计特性的图像修复方法，都能在一定程度上缓解此问题。但PatchMatch算法采用随机初始化的方法来获得图像的偏移映射图，虽然可以提高算法的运行效率,但也会降低算法的匹配精度，造成算法的修复质量的下降。为了有效提高该算法的匹配精度,改善算法的最终修复质量，本文提出将图像先验特性作为约束条件对图像的偏移映射图进行约束初始化，从而起到提高算法匹配精度的目的；考虑到本文算法的时效性，利用图像的相似块的偏移值具有稀疏性[7]这一图像统计特性来减少用于修复图像的标签集合的数量，从而起到提高算法运行效率的目的。改进后的算法主要分为五个步骤，其流程如图1所示。

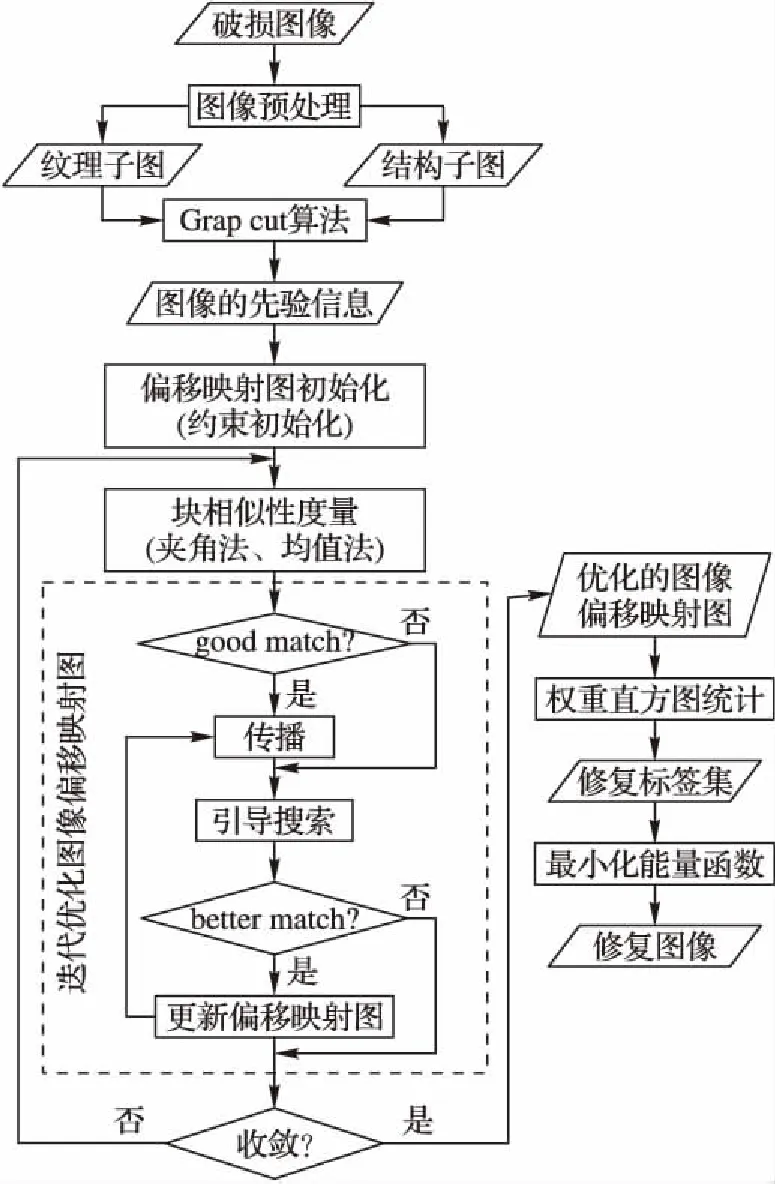
图1　算法流程Fig. 1　Algorithm flowchart

步骤1利用文献[14]中相对全变差的方法对破损图像进行预处理分离出图像中完好部分的纹理信息和结构信息，以此获得图像的先验信息。

步骤2利用Grab cut算法[15]和上一步骤预处理获得的先验信息对破损图像中的完好部分进行区域分割，使得图像中具有相同结构信息和纹理信息的像素块划分到同一区域。对各子区域内部像素块的偏移值进行约束，即分配给像素块的偏移值只能来自各子区域内部除其本身以外的其他像素块的相对位置，以此实现对图像的偏移映射图的约束初始化。

步骤3初始化完成后，每个像素块被分配了一个偏移值，通过这个偏移值就可以找到其匹配块的相对位置。利用改进的相似性度量公式对分配给像素块的匹配块进行相似性判断。若判断结果为好的匹配块(good match,本文通过实验仿真后，对于结构块夹角小于0.5或纹理块差值小于0.004的块定义为好的匹配块)，将匹配信息向邻域像素块传播,邻域像素块等得其匹配信息后,执行引导搜索看是否有更好的匹配块(better match，其值要小于good match)，若找到更好的匹配块,则更新像素块的偏移值,向其邻域像素块传播其更新后的匹配信息；若没有找到更好的匹配块，则直接将接收到的匹配信息向其邻域传播。若判断结果为坏的匹配块，直接执行引导搜索找到好的匹配块后再执行传播。重复以上操作直至算法收敛，得到优化的图像偏移映射图。

步骤4获得优化的图像偏移映射图后，对图像的偏移映射图进行直方图统计，取峰值较高的前P(本文实验为P=65)个偏移值作为图像的主要偏移值，组成图像的修复标签集。

步骤5获得图像的修复标签集后，本文将图像修复问题看成是向未知像素点/块分配一个标签(偏移值)，未知像素点在这个偏移值的指导下在完好区域找到相应的最优匹配块并把匹配块填充到未知像素点的位置。在上述过程中用MRF能量函数来优化图像的修复效果。至此就完成了整个图像的修复过程。

2　匹配精度的提高

2.1　约束初始化

基于图的图像修复算法[7]中对于偏移映射图的初始化比较敏感。而PatchMatch算法中采用随机的方式对图像的偏移映射图进行初始化会降低算法的匹配精度。在图像处理领域中，图像先验信息对图像修复具有重要的指导意义。为了提高算法的匹配精度，本文方法的主要改进是在PatchMatch算法的初始化阶段引入图像的先验特性，然后利用该图像的先验特性对图像的偏移映射图的初始化进行约束，而不再采用原PatchMatch算法随机初始化的方法，以提高图像修复的最终修复效果。

由引言可知，图像偏移映射图的初始化的优劣会直接影响基于图(graph-based)的图像修复算法[7]中修复效果的好坏。由于图像具有局部自相似性[13]和纹理平滑性[17]，可以根据纹理和结构具有不同的先验信息来指导图像偏移映射图的初始化过程，以此实现对图像偏移映射图在先验信息指导下的约束初始化，从而达到提高像素块匹配精度、减少算法误匹配的目的。具体操作步骤如下：

首先，在图像偏移映射图的初始化阶段采用相对总变差[14]的方法对原图像进行预处理，分离出原图像纹理信息和结构信息；然后，按照原图像中的结构信息和纹理信息结合Grab cut算法[15]对原图像进行区域分割，使得几何结构和纹理信息相似的像素块划分到同一区域内。约束初始化的过程和处理结果如图2所示。

图2　约束初始化过程实例图Fig. 2　Instance of constrained initialization process

其中：图2(a)为含有纹理结构和几何结构的测试图像；图2(b)为该图经过预处理后含有图像细节信息的纹理子图；图2(c)为预处理后含有图像几何轮廓信息的结构子图；图2(d)为预处理后的先验约束图，其中的方块表示像素块(patch)。图2(d)中不同的灰度代表几何结构和纹理信息不同的图像局部子区域，在各子区域内像素块的几何结构和纹理信息相似。

其次，在划分好的图像局部区域内采用组内随机初始化的方式为局部区域内的各像素块分配偏移值。如图3所示，A、B、C、D分别为按照上一步图像预处理后，按照先验信息分割成的图像局部子区域，各局部子区域内像素块的偏移值来自各像素块所在的区域内部的像素块,即分配给A区域的像素块Ai的偏移值T(Ai)及在此偏移值下所找到Ai的匹配块Aj也必须和Ai属于同一区域。组内随机初始化的公式如式(1)所示。

T(pi)=si-random(sj)；i≠j∪i,j∈N(seg)

(1)

式中:si=(xi,yi)为像素块Ai的中心坐标，sj=(xj,yj)为Aj的中心坐标,Ai和Aj表示在同一图像局部区域(seg)内的像素块;T(·)=(u,v)为像素块的偏移值;N(seg)表示图像局部区域(seg)的邻域;random(·)表示采用随机的方式获得一个像素块的坐标。

图3　组内随机初始化示意图Fig. 3　Schemetic diagram of random initialization in a group

最后，为各图像局部区域已初始化完成的偏移子图即各个图像局部区域内的像素块都分配一个偏移值。依据原图像的尺寸大小，按照计算机的扫描顺序对各图像局部区域的像素块进行排序，排序完成后就得到了整幅图像的偏移映射图,从而完成对图像偏移映射图的约束初始化过程。

2.2　相似块度量公式的改进

经过约束初始化后，图像中每个像素块都被分配了一个偏移值；然后，利用相似性判断公式对分配其的匹配块进行相似性判断，以判断该匹配块是不是最优匹配块。传统的图像修复算法通常采用离差平方和(Sum of Squares of Deviations，SSD)来度量两个像素块的相似性，此类方法不能较好地区分结构信息和纹理信息。为了使算法能够较好地区分像素块中的结构信息和纹理信息，达到提高算法的匹配精度的目的，本文利用预处理阶段获得图像先验信息将图像的像素块分为结构块和纹理块，针对不同类别的像素块采用不同的相似性度量方法。通常情况下，结构块会包含较多的几何结构信息，而这些结构信息在结构块中具有一定的方向性；因此，提取出结构块中的几何结构信息和方向信息组成结构块的主结构方向向量，然后采用判断两个结构块之间主结构方向向量夹角大小的方式判断其相似性，夹角越小越相似。具体如式(2)所示：

(2)

式中:s(i)表示以i=(x,y)为中心的结构patch块的主结构向量;T=(u,v)为偏移值；θi,i+T为以i=(x,y)为中心的patch和在偏移值T下得到的patch之间的主结构向量夹角。

对于纹理块，由图像的纹理具有局部平滑性[17]的先验特性可知，图像的局部区域内纹理变化不明显，这也表明局部区域内的纹理块的均值变化不明显。据此，采用判断图像像素块纹理均值之间差值的大小来判断其相似性，差值越小越相似。具体如式(3)所示：

|E[t(i)]-E[t(i+T)]|≤ε

(3)

式中：t(i)为以i=(x,y)为中心的纹理块；E[·] 表示纹理块的均值;T=(u,v)为偏移值;ε为一个极小的正值。

与原算法中采用的SSD评价相似性度量的判断相比,改进的相似性判断方法很好地区分了像素块中的结构和纹理信息，使算法的匹配精度有所提高，这可从文中第5章的实例仿真中体现出来。

2.3　引导搜索

经过相似性度量后，获得了图像偏移映射图中哪些像素块被分配了好的匹配块(good match)和哪些像素块没有被分配好的匹配块的信息。对于那些分配给好的匹配块的像素块，PatchMatch算法中利用指数下降距离(exponentially decreasing distance)的方法[13]在全局范围采用随机的方式逐步缩小搜索范围直至缩小到一个像素点大小后停止搜索，查找是否有最优匹配块(better match),以此来提高算法的匹配精度。

由图像纹理平滑性和局部自相似性的图像先验特性可知，目标块的最优匹配块出现在该目标块周围区域的概率较大，且在图像的局部区域内相似的像素块沿着纹理具有主要的扩散方向。因此，相比原算法采用随机查找的方式在全局查找更新最优匹配块的方法，本文采用引导搜索方法，即按照局部区域内的图像纹理扩散的方向，在目标块相邻的局部区域内搜索其最优匹配块，这样能进一步提高算法的匹配精度。图4为引导搜索的示意图(图中ncur(cur=i,j,p)为像素点cur处的法向量)。

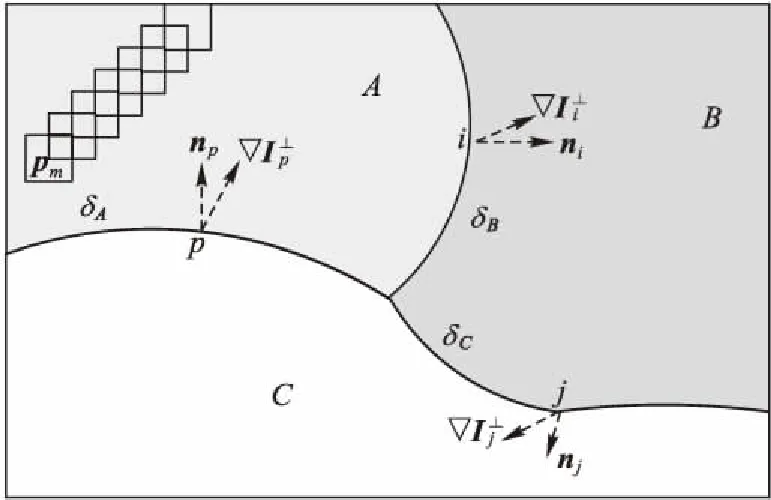
图4　引导搜索示意图Fig. 4　Schematic diagram of guided search

引导搜索的详细操作过程如下：

1)利用Canny算子分别对经过图像预处理后的图像分割区域进行边缘检测，以得到各分割区域的边缘，图中δA、δB、δC分别表示区域A、B、C的边界。

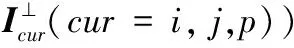
(4)

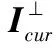
3)确定了每个区域的主要纹理扩散方向后，沿着该区域边界的纹理扩散方向，在各自区域内对所属区域的样本块按照本区域的主要纹理扩散方向去进行引导搜索，查找相应的匹配块(如式(5)所示)，提高算法的匹配精度，迭代优化图像的偏移映射图。

offset(pm)=(ncos(θm),nsin(θm))

(5)

其中:pm表示以m=(x,y)为中心的像素块patch，offset(·)表示该像素块的偏移值，θm为像素块pm所在图像分割子区域的纹理扩散方向，n=1,2,…直到偏移值处于边缘位置。

3　时间效率的改进

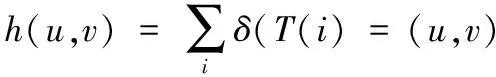
(6)

其中，T(i)=(x,y)表示以i为中心的像素块的偏移值。当上述公式成立时，δ(·)的值取1，不成立时取0。

偏移值的数量选取得越少越能提高算法的运行速度，但对修复质量会造成一定程度的下降，以峰值信噪比(Peak Signal-to-Noise Ratio， PSNR)和算法的运行时间(Runtime)两项作为客观标准来验证偏移值的选取对算法性能的影响。对比了以下两种实例：1)纹理结构和几何结构都比较丰富的图片(情形1),如唐卡；2)纹理结构和几何结构单一或者图片有较多重复结构的图片(情形2),如天空、湖面和建筑等。结果如表1所示。

表1　不同偏移值数量下峰值信噪比和运行时间的比较Tab. 1　Comparison of PSNR and running time for different offset values

由表1数据可知:结构和纹理单一的破损图像(情形2)对主要偏移值数量的选取不敏感；而结构和纹理较丰富的破损图像(情形1)对主要偏移值的数量选取较敏感，即选取的偏移值数量和算法的修复质量呈线性关系，选取的偏移值越多，算法的修复质量越好，但运行时间会增加。为了发挥出改进算法的最佳性能，从算法的运行时间和峰值信噪比两方面值综合考虑，最终选取主要偏移值的数量为P=65作为实验参数。

4　图像修复效果的改进

获得了图像的样本标签集后，原算法采用最小化MRF能量函数来约束向未知像素点分配的标签来实现修复破损图像的目的。但是原算法的能量函数中的平滑项只考虑了图像的颜色信息，没有将图像的结构信息的重要性考虑进去，而结构在视觉感知中作用尤为重要。在图像修复过程中经常先修复图像的结构部分以保持整体图像一致性，若忽略结构信息的重要性，使用纹理先进行填充，会出现细节相似但整体产生偏差的情况。

综上可知，在图像的修复过程中，对图像修复过程进行结构约束，以突出图像的结构信息的重要性，可以有效提高修复算法的修复质量。数字图像中，图像的梯度变化能够反映出图像的结构信息，因此，在原平滑项公式中引入梯度因子来约束图像的修复过程，以使改进后的平滑项公式在满足相邻像素块的颜色值相似的同时也满足梯度变化的相似性，从而有利于保持修复图像的结构信息，提高修复算法的修复质量。本文算法采用优化以下最小化能量函数来修复破损图像：

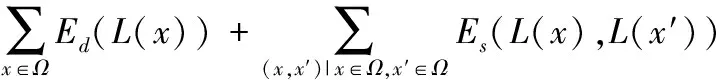
(7)

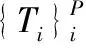
如果向未知像素点分配的标签是有效值，即以x+T为中心的像素块处于图像的完好区域，数据项(Ed)的值为0；其他情况下，数据项的值为+∞。

改进后的平滑项公式(Es)加入了梯度算子，使得平滑项公式在满足用来惩罚接缝同时也满足惩罚修复算法中结构不一致的情况。改进后的平滑项公式如下：

Es=α‖I(x+Ta)+I(x+Tb)‖2+

α‖I(x′+Ta)+I(x′+Tb)‖2+

β|▽I(x+Ta)+▽I(x+Tb)|+

β|▽I(x′+Ta)+▽I(x′+Tb)|

(8)

式中：I(x)是像素点x的RGB颜色值;Ta、Tb分别为像素点x分配的偏移值和为像素点x′分配的偏移值；I(·+Ta)、I(·+Tb)分别表示在偏移值为Ta或Tb时得到的偏移映射图；▽I(·+Ta)、▽I(·+Tb)分别为偏移映射图为I(·+Ta)、I(·+Tb)时的梯度值；α和β为平衡颜色信息和结构信息所占的比重。当未知像素点x和其邻域x′被分配了不同的偏移后，出现接缝或者结构断裂的情况，上述平滑项会对其进行惩罚以达到较好的修复效果。

5　实例验证与分析

为了验证本文算法的有效性，在配置Intel Core i5 2.5 GHz CPU和4 GB RAM的计算机上进行了实验，实验环境为Visual Studio 2015版本。实验中的对比算法包括：文献[7]中提出的相似块统计算法、文献[9]中提出的贪婪类算法、文献[13]中提出的PatchMatch算法和本文算法。采用峰值信噪比和算法运行时间作为算法的客观评价标准，峰值信噪比的计算公式如下：

(9)

图5分别给出了四种算法对pumpkin图像(512×512)的修复效果。文献[7]中的相似块统计算法在修复破损区域时在结构的交汇处(图中圆圈标记处)出现了纹理延伸现象，使结构看起来不自然；文献[9]中的贪婪类算法在修复破损区域时，在玻璃处纹理延伸的同时引入了误匹配且出现结构断裂；文献[13]中的PatchMatch算法在结构处出现断裂和纹理的错误延伸;本文算法结构处连续，纹理扩散自然，具有很好的视觉效果。

本文也对图像的划痕消除进行了仿真，结果如图6所示。可以看出相似块统计算法、贪婪类算法和PatchMatch算法都在Lena(283×282)眼睛处进行纹理延伸时出现了模糊现象,而本文算法虽然也出现了一定的模糊现象，但相较前者程度较轻。

本文还对纹理和结构都比较丰富的唐卡图像(430×596)进行了仿真，结果如图7所示。相似性统计算法由于平滑项中没有考虑到结构约束，在修复时出现了结构断裂，导致了纹理的错误延伸；贪婪类算法在填充纹理时由于本身的贪婪性会造成一定的误匹配并产生了一定的模糊现象；PatchMatch算法纹理延伸时出现误匹配，导致结构断裂使得修复结果看起来不自然；本文算法修复效果较好，且没有出现误匹配现象和纹理延伸。

四种对比算法的峰值信噪比和算法运行时间对比如表2所示。从表2数据可以看出，本文算法不仅能更好地满足人眼视觉效果要求，而且在客观评价指标上优于相关算法，而且本文算法相比PatchMatch算法具有较大的优势。

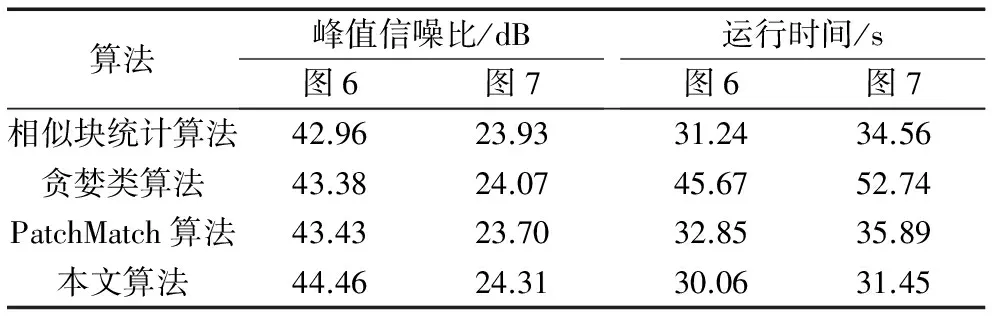
表2　四种修复算法的峰值信噪比和运行时间比较Tab. 2　Comparison of PSNR and running time for four kinds of inpainting algorithms

图5　pumpkin修复效果比较Fig. 5　Inpainting effect comparison of pumpkin

图6　Lena修复效果比较Fig. 6　Inpainting effect comparison of Lena

图7　唐卡修复效果比较Fig. 7　Inpainting effect comparison of Thangka

6　结语

本文提出的基于先验约束和统计的图像修复算法充分利用了图像的先验特性来约束图像偏移映射图的初始化，并对传统的基于SSD值的相似性评价方法进行了改进，使其能够区分图像块中的结构部分和纹理部分的相似性，从而提高匹配精度；最后还利用图像的统计特性来减少算法的运行时间。仿真实验分析结果表明，相比PatchMatchs算法和其他相关算法，本文算法不仅具有较高的匹配精度而且收敛速度有所提高，取得了更好的修复效果。但是对于结构信息和纹理信息不是很丰富的图像，本文的改进算法仍难以得到自然的修复效果。在今后的研究工作中，我们将尝试根据图像的结构信息和纹理信息丰富程度，使算法能自适应地调整优化能量函数平滑项中颜色信息和结构信息所占比重的参数，以此来进一步改善算法的效率和修复效果。

参考文献:

[1]GUILLEMOT C, LE MEUR O. Image inpainting: overview and recent advances [J]. IEEE Signal Processing Magazine, 2013, 31(1): 127-144.

[2]王猛,翟东海,聂洪玉,等.邻域窗口权重变分的图像修复[J].中国图象图形学报,2015,20(8):1000-1007. (WANG M, ZHAI D H, NIE H Y, et al. Image inpainting with weight variation of neighborhood window [J]. Journal of Image and Graphics, 2015, 20(8): 1000-1007.)

[3]BERTALMIO M, SAPIRO G, CASELLES V, et al. Image inpainting [C]// SIGGRAPH ’00: Proceedings of the 27th Annual Conference on Computer Graphics and Interactive Techniques. New York: ACM, 2000: 417-424.

[4]CHAN T F, SHEN J. Mathematical models for local nontexture inpaintings [J]. SIAM Journal on Applied Mathematics, 2002, 62(3): 1019-1043.

[5]ELAD M, STARCK J-L, QUERRE P, et al. Simultaneous cartoon and texture image inpainting using Morphological Component Analysis (MCA) [J]. Applied and Computational Harmonic Analysis, 2005, 19(3): 340-358.

[6]YU G S, SAPIRO G, MALLAT S. Solving inverse problems with piecewise linear estimators: from Gaussian mixture models to structured sparsity [J]. IEEE Transactions on Image Processing, 2012, 21(5): 2481-2499.

[7]HE K, SUN J. Image completion approaches using the statistics of similar patches [J]. IEEE Transactions on Pattern Analysis And Machine Intellignce, 2014, 36(12): 2423-2435.

[8]EFROSA A， LEUNG T K. Texture synthesis by non-parametric sampling [C]// ICCV ’99： Proceedings of the Seventh IEEE International Conference on Computer Vision. Washington, DC: IEEE Computer Society, 1999, 2: 1033-1038.

[9]CRIMINISI A, PEREZ P, TOYAMA K, et al. Region filling and object removal by exemplar-based image inpainting [J]. IEEE Transactions on Image Processing, 2004, 13(9): 1200-1212.

[10]WEXLER Y, SHECHTMAN E, IRANI M. Space-time video completion [C]// CVPR ’04： Proceedings of the 2004 IEEE Computer Society Conference on Computer Vision and Pattern Recognition. Washington, DC: IEEE Computer Society, 2004: 120-127.

[11]KOMODAKIS N. Image completion using global optimization [C]// CVPR ’06： Proceedings of the 2006 IEEE Computer Society Conference on Computer Vision and Pattern Recognition. Washington, DC: IEEE Computer Society, 2006: 442-452.

[12]PRITCH Y, KAV-VENAKI E, PELEG S. Shift-map image editing [C]// ICCV ’09: Proceedings of the IEEE 12th International Conference on Computer Vision. Piscataway, NJ: IEEE, 2009: 151-158.

[13]BARNES C. PatchMatch: a fast randomized matching algorithm with application to image and video [D]. Princeton, NJ: Princeton University, Department of Computer Science, 2011: 103-110.

[14]LI X, QIONG Y, YANG X, et al. Structure extraction from texture via relative total variation [J]. ACM Transactions on Graphics, 2012, 31(6): Article No. 139.

[15]ROTHER C, KOLMOGOROV V, ANDREW BLAKE. “GrabCut”: interactive foreground extraction using iterated graph cuts [J]. ACM Transactions on Graphics (TOG) — Proceedings of ACM SIGGRAPH 2004, 2004, 23(3): 309-314.

[16]KORMAN S, AVIDAN S. Coherency sensitive hashing [C]// ICCV ’11: Proceedings of the IEEE 2011 International Conference on Computer Vision. Washington, DC: IEEE Computer Society, 2011: 1607-1614.

[17]ZHANG J, ZHAO D, XIONG R, et al. Image restoration using joint statistical modeling in space-transform domain [J]. IEEE Transactions on Circuits and Systems for Video Technology, 2014, 24(6): 915-928.

[18]王佳君，俞强，张晶晶，等.基于先验置信传播的图像修复改进算法[J].计算机应用，2016,36(4):1115-1119. (WANG J J, YU Q, ZHANG J J, et al. Improvement algorithm of image inpainting based on priority-belief propagation [J]. Journal of Computer Applications, 2016, 36(4): 1115-1119.)

[19]SIMAKOV D, CASPI Y, SHECHTMAN E, et al. Summarizing visual data using bidirectional similarity [C]// CVPR ’08： Proceedings of the 2008 IEEE Computer Society Conference on Computer Vision and Pattern Recognition. Washington, DC: IEEE Computer Society, 2008: 1-8.