多个体切换网络分布式量化次梯度优化算法

李甲地，马　驰，李德权，王俊雅

(安徽理工大学 数学与大数据学院，安徽 淮南 232001)(*通信作者电子邮箱1378475744@qq.com)

0　引言

由于因特网、移动互联网和无线传感网络等大规模网络的出现，多个体网络分布式优化成为一个研究热点。分布式优化要求所设计的算法仅基于网络中个体间的局部信息通信协调，即可求解网络目标函数的最优值。例如，并行计算[1]、数据研究[2-3]、机器人研究[4]或无线网络资源的分配问题[5]等都可归结为分布式优化算法。

现有的多个体网络分布式算法一般都基于一致性算法，且都基于一个理想化的假设:即构成网络的个体间通信的是各个个体某个状态变量的完全精确的信息。这意味着如果传输的状态变量是实值情形，则要求网络通道具有无限带宽，且算法能够以无限精度被执行。此外，还通常假定网络中个体间的信息交流是平衡的，这其实要求网络拓扑是有向平衡的。而这些条件在实际应用中过于苛刻。例如,Google之所以能成为搜索引擎霸主，其技术原因是第一个把WWW真正视为“网(Web)”的搜索引擎[6]。Google的网页排序技术PageRank算法把所有网页构成的网页网络视为有向非平衡网络，并且所构成的网页网络是随着时间动态切换的。显然，现有的关于网络是有向平衡图的理想化假设并不适用，考虑更一般的切换有向非平衡网络更有必要。

因为多个体网络有空间分布特性，个体间通常基于远程通信和无线传感网络实现信息共享[7]。尤其是网络运行在非常恶劣的环境中时，由于数据丢包或节点的连接失败，或不同个体有不同的感知范围，往往一样会造成网络个体间的通信网络是有向非平衡的。例如，在多移动车辆系统的编队控制中，由于不同车辆具有不同的感知范围,或有些车辆仅装备信息发射器或接收器，同时可能因障碍物阻断或消失，使得构成的通信网络是一个有向非平衡切换网络[8]。战斗机编队在恶劣天气中执行飞行任务，由于通信连接失败或重连，使得构成的通信网络也是一个典型的有向非平衡切换网络。对于有向非平衡网络，不仅意味着更弱的网络拓扑条件，还意味着所设计的优化算法不需要额外的通信成本用于信息回复，降低网络个体达到一致性所需的信息量。而且个体间的信息传输受无线通信网络带宽限制，导致个体间信息交流之前个体状态信息通常是量化的而非精确信息。因此，文献[9-10]将网络拓扑和量化信息统一考虑，考虑了更一般的非平衡网络，研究了基于量化信息通信的量化一致性问题。

一般来说，分布式无约束优化问题主要有两种不同的方法:基于次梯度的方法和无梯度的方法。在假定每个个体的目标函数是凸的但不一定光滑的情形下，文献[11-12]提出的分布式算法可确保每个个体产生并保持其对全局最优解的估计，并且与其邻居在时变网络上进行信息交流来更新自身状态。文献[13-15]介绍了量化一致性算法的编码/解码策略，研究了量化一致性。

最近，文献[16]针对切换多个体网络中个体仅与其邻居个体通过量化信息进行平衡交流，亦即所对应的通信网络为有向平衡网络,提出量化分布式次梯度投影优化算法解决了带约束的平均一致性优化问题。显然，文献[16]中所提算法并不适用于文献[8]中类似情况。文献[16]还在文中考虑了确定性量化器和概率量化器两种类型[17-19]，分析了量化信息交流对算法的收敛性的影响，但它所给出的量化器具有无限量化水平以及仅考虑在切换有向平衡网络中，因此本文采用具有有限量化水平的一致对称量化器及相关量化策略[9,20-21]，针对更一般的切换有向非平衡多个体网络提出了基于量化信息通信的分布式量化次梯度优化算法。研究表明在相同的通信网络带宽的条件下，个体与其邻居个体交换量化信息进行非平衡交流，可提高信息传输速率，使得多个体网络中个体更快地达到一致。

1　问题描述与量化通信策略

1.1　问题描述

考虑有m个个体的切换非平衡网络，其通信网络可建模成一个有向图G(t)=(V,E(t),A(t))。其中：V={1,2,…,m}是节点集；边集E(t)⊂V×V；A(t)=(aij(t))m×m表示有向图G(t)所对应的随机邻接矩阵，其中aij(t)表示有向边(j,i)的权重，刻画了个体j向个体i发送信息的可信度。由于本文考虑带有自环的切换平衡网络，所以定义Ni(t)={(j,i)∪(i)∈E(t)|i,j∈V}是个体i在t时刻的入度邻居集合，表示t时刻发送信息给个体i的全体个体。考虑如下分布式无约束优化问题:

(1)

s.t.x∈Rn

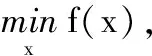
1.2　相关假设

假设1 最优解为X*={x∈Rn|f(x*)=f*}是存在的。

假设2对于每个个体i∈V，与其对应的目标函数fi在Rn上是凸函数但不一定可微，并且存在常量G>0使得对所有的i∈V有

‖di(x)‖≤G，∀di(x)∈∂fi(x)，x∈Rn

其中，∂fi(x)表示函数fi在x处的所有次梯度的集合。

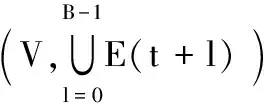
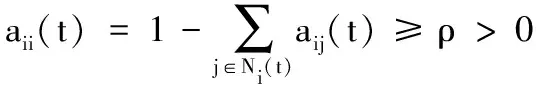
1.3　量化器及编译码协议

考虑动态切换有向非平衡网络，由于信道的容量或带宽受限，个体必须在将信息发送给其邻居个体之前量化信息,这里将借鉴基于边的自适应动态一致量化器的量化通信策略[9，20-21]。定义具有有限量化水平的动态一致量化器如下：

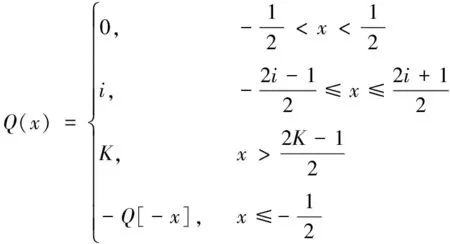
(2)

其中：x是一个实数，K是一个正整数。量化水平集Γ={0,±i,i=1,2,…,K}，其仅含有有限的元素。事实上，式(2)中量化器Q(x):R→Γ是R到量化水平集Γ的映射。

为了降低通信成本，提高信息传输效率，为网络中每个个体的信道提出编码译码协议，以获得从邻居个体发送的状态估计值。对发送个体j对应的有向边(j,i)的编码器Φji的编码算法定义如下：

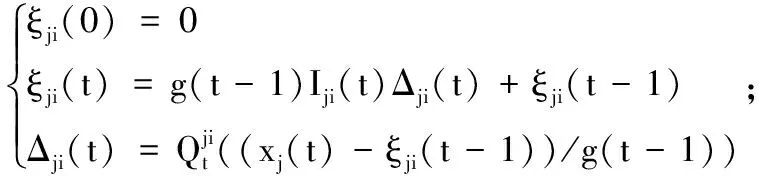
t=1,2,…

(3)

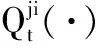
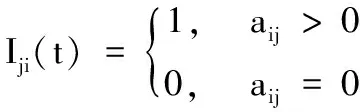
(4)

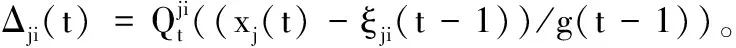
为了确保个体i在t时刻可以接收到j的估计值Δji(t)(具有某种的量化误差)，与个体j相关联的通信信道(j,i)∈E的解码器Ψji定义如下：

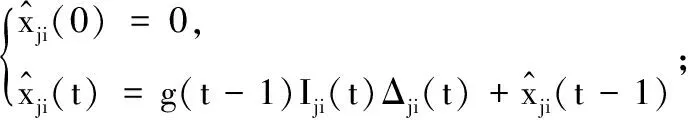
t=1,2,…

(5)

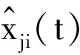
并由式(3)和(5)知：

(6)

2　分布式量化次梯度优化算法与收敛性分析

2.1　分布式量化次梯度优化算法

下面介绍在切换非平衡网络中的量化分布式次梯度优化算法，其中每个个体仅与其邻居个体交换量化信息。xi(t+1)表示个体i在t+1时刻的状态，个体i接收来自其邻居j∈Ni(t)发送的量化信息，先计算这些状态的加权平均值，然后通过使用它们各自的次梯度信息执行局部优化。本文针对问题(1)有如下量化分布式次梯度优化算法:

(7)

xi(t+1)=yi(t)-αtdi(t)

(8)

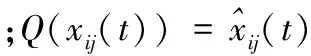
2.2　收敛性分析

由于通信网络所对应的是切换有向非平衡图，所以文献[22]主要基于转移矩阵φ(t,s)的性质来证明算法收敛性的方法对本文所研究问题将不再适用。受文献[14,21]启发，下面利用非二次李雅普诺夫函数方法[21，23]以及文献[24]中的部分相关结论来证明有向非平衡图的量化分布式次梯度优化算法的收敛性。

先定义:

并进一步定义：

D(t)=M(t)-m(t),ΔR(t)=Δrmax(t)-Δrmin(t)。

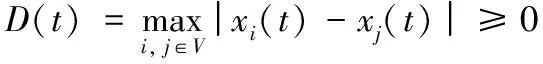
eji(t)=xj(t)-ξji(t)

(9)

Eij(t)=(xj(t+1)-ξji(t))/g(t)-Δji(t+1)

(10)

将假设4，式(6)、(7)和(9)代入式(8)，改写为如下形式：

(11)

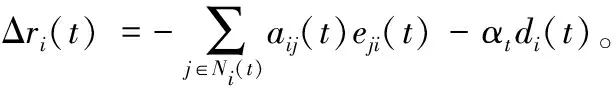
根据矩阵A(t)的随机性，可得：

因此可得如下关系式:

(12)

此外，对假设3有，对于任意正整数s≥0，令个体κ∈V，并定义集合D0={κ}。由假设3可知，一定存在一个非空集合D1=VD0使得在时间间隔[s,s+(B-1)]内对于任意i∈D1，个体κ都与其至少发生一次信息交换。类似地，通过数学归纳法可知，存在这样一个集合Dl+1⊂V(D0∪D1∪…∪Dl)，使得在时间间隔[sl,s+((l+1)B-1)]内一定存在某个个体i∈(D0∪D1∪…∪Dl)与个体j∈Dl+1至少交换一次信息。由假设3进一步可知，只要V(D0∪D1∪…∪Dl)不等于空集，则Dl+1不等于空集。因此，集合D0∪D1∪…∪DL是个体集合V的一个分割，其中L≤m-1。

所以，本文提出的量化分布式次梯度优化算法(7)和(8)以及变式(11)，与文献[24]中所提出的一阶动态一致性算法具有完全相同的形式；当假设3，4以及式(12)成立时，满足文献[24]中引理3.1的所有假设条件。因此，下面借用文献[24]中引理3.1的相关结论给出如下引理1及定理1。

引理1假定假设3和4成立，令s≥0且固定k∈V，集合D0∪D1∪…∪DL是个体集合V的一个分割，则对任意l∈{1,2,…,L}(L≤m-1)，一定存在μl>0，其中满足μ0=ρmB-1，使得对正整数p∈[LB,LB-1]和i∈Dl，当t=s+p时，如下两式成立：

(13)

(14)

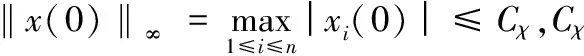
(15)

证明由引理1有

μ(M(k)-xκ(k)+xκ(k)-m(k))≤

此外，对正整数h≥1，定义h(mB-1)=Th。进而对任意的正整数t≥1，令s为满足s(mB-1)=Ts≤t<(s+1)(mB-1)的最大整数，从而可得:

(16)

其中，Ω(t)为

2αtGi|[(1-μ)s-1+(1-μ)s-2+…+(1-μ)+1]≤

(17)

证毕。

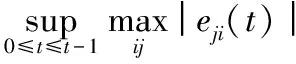
eji(t+1)=g(t)Εij(t)

(18)

由式(18)可知，如果量化误差Eij(t)有界，当t→∞时，g(t)→0，则估计误差渐近趋于0，而成立的关键是如何设计动态比例函数g(t)以及量化水平参数Kji(t)，所以有如下定理2。

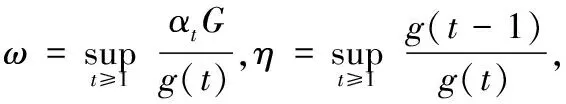
(19)

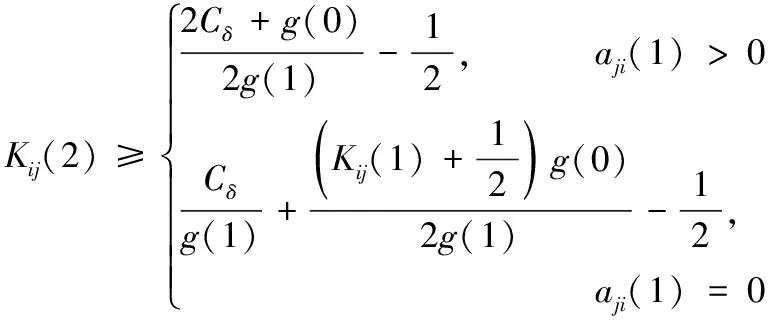
(20)

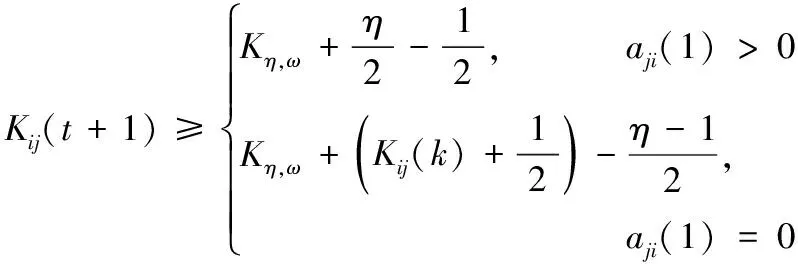
(21)

其中:

(22)

那么在量化次梯度算法(7)、(8)的作用下，式(11)满足：

(23)

若当t→∞时g(t)→0(t→∞)，则有：

即系统中的个体达到一致。

证明由eji(t)、Eij(t)以及式(3)、(6)，可以得到：

aij(t)eij(t)=aij(t)g(t-1)Eij(t-1)

(24)

则式(11)可写为：

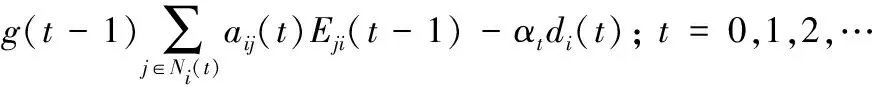
(25)

由式(3)、(4)知：

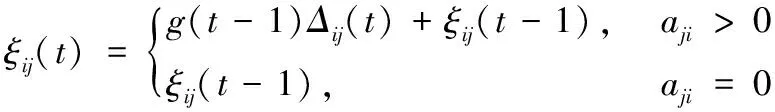
(26)

当aji>0时，再由式(18)、(26)可得：

g(t-1)Eij(t-1)=xi(t)-ξij(t-1)-g(t-1)Δij(t)

(27)

进而利用A(t)是随机矩阵以及式(27)可知：当aji>0时，即有向边(i,j)在第t时刻连通，则下式成立：

(28)

当aij=0时，即有向边(i,j)在第t时刻断开，有类似式(28)的不等式成立。

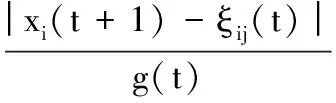
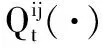
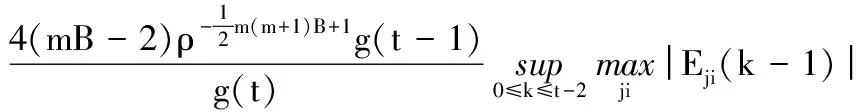
(29)

则由式(28)知，当aji>0时有式(30)成立：

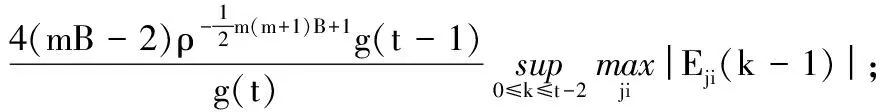
t=1,2,3…

(30)

同理，当aji=0时，类似不等式成立。

下面利用数学归纳法对式(11)进行收敛性分析。

由定理1和式(19)及ξij(0)=0可知：

(31)

由式(2)定义的一致量化器的性质和式(6)，则有

(32)

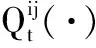
同理，当aij(1)>0，由式(20)和(28)可得：

(33)

当aij(1)=0，则有类似式(33)的不等式成立。

综合上述两种情况可知：

(34)

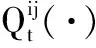
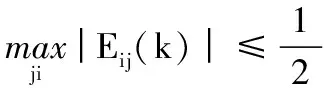
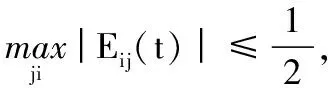
(35)

当aij(t)=0时，有类似式(35)的不等式成立。

其中推导过程利用了定理2的假设条件，易推得:

(36)

综合上述可得:

(37)

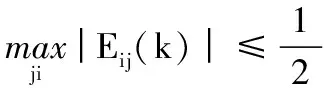
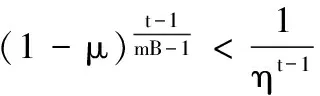
t→∞

(38)

当t→∞时g(t)→0，有定理2成立，即所有个体达到一致。

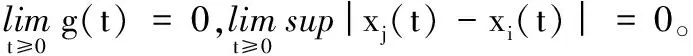
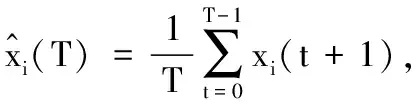
(39)

其中D(t)由定理2给出。

证明证明全局函数f(x)收敛到最优值f(x*)，有以下不等式成立:

(40)

由假设2，有

f(xi(t+1))-f(x*)≤

(41)

考虑到fi(xi(t+1))-fi(x*)，有以下不等式成立:

fi(xi(t+1))-fi(x*)≤

G‖xi(t+1)-yi(t)‖+〈di(t),yi(t)-x*〉≤

GD(t)+〈di(t),yi(t)-x*〉

(42)

将式(42)代入式(40)，并由文献[16]中引理3及文献[25]有下式成立，定理3即证。

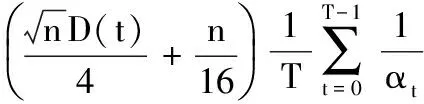
由定理3可知，在分布式量化次梯度算法(7)、(8)作用下，全局目标函数f(x)渐进地收敛到最优值f(x*)。

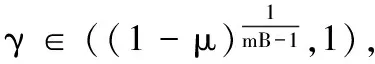
3　仿真分析

为了验证本文所提算法理论，考虑由4个个体组成的带有自环的有向切换非平衡网络G(t)=(V,E(t))。其中个体集合为V={1,2,3,4}，E(t)是个体在t时刻的边集，个体的局部目标函数为fi(x)=(x-ai)2,ai∈R(i=1,2,3,4)。有向切换非平衡网络周期B=3的有向联合图表示如下:E(3t)∪E(3t+1)∪E(3t+2)=E(a)∪E(b)∪E(c),说明在某个时刻所对应的通信网络图是弱连通的，也就是说个体间进行的信息交流是不充分的；但在一个切换网络周期B内，其联合图是强连通的，保证了个体间信息的充分交流。一个周期内各个子图对应的随机邻接矩阵A(t)如下:

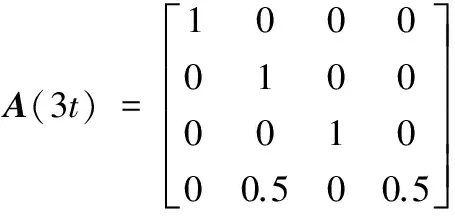
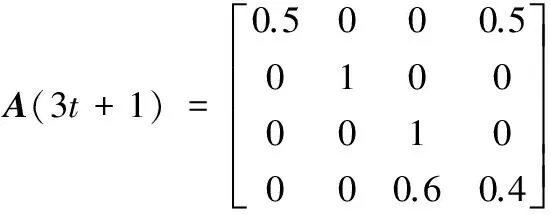
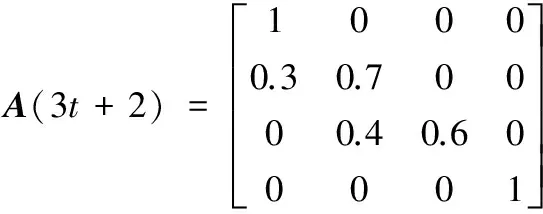
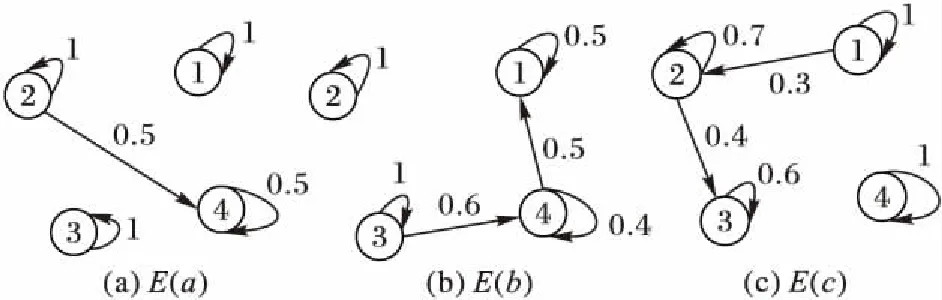
图1　4个个体的有向切换网络Fig. 1　A switching directed network with four nodes

图2表示γ=0.978 8时4个个体的状态轨迹图，当迭代次数达到250左右，在误差允许的范围内，多个体网络中的所有个体状态值达到一致，其状态最优值在3的邻域内。图3表示γ=0.878 8时4个个体的状态轨迹图，通过对量化参数γ进行调节，迭代次数仅达到50后，多个体网络中的所有个体状态值达到一致，其状态最优值也在3邻域内。图2和图3表明：网络中所有个体通过非平衡信息交流在分布式量化次梯度算法的作用下最终达到一致，并且通过调节量化参数γ可提高网络中个体的收敛速率，γ越小收敛越快，降低了对网络带宽的要求。

图4表示γ=0.978 8以及γ=0.878 8时全局目标函数的误差。图4表明：γ=0.978 8和γ=0.878 8的全局目标函数的误差渐进地趋于零，表明在所提分布式量化次梯度算法的作用下，多个体网络中个体最终达到一致，且在一致性值时全局目标函数达成最优。此外，由全局函数误差下降速度可知，当γ=0.878 8时收敛更快。这也说明在相同的网络带宽下，通过调节量化器的参数，可使整个网络以更快收敛速率实现优化目标，从而减少对网络无限带宽的依赖。

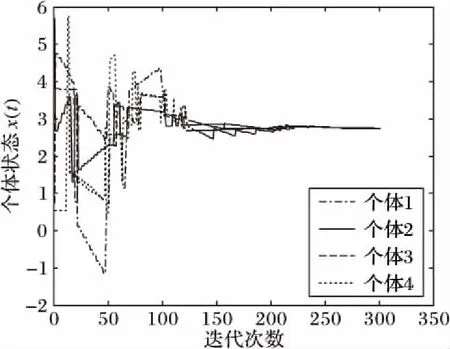
图2　γ=0.978 8时4个个体的状态轨迹Fig. 2　Trajectories of four agents’ states with γ=0.978 8

图3　γ=0.878 8时4个个体的状态轨迹Fig. 3　Trajectories of four agents’ states with γ=0.878 8

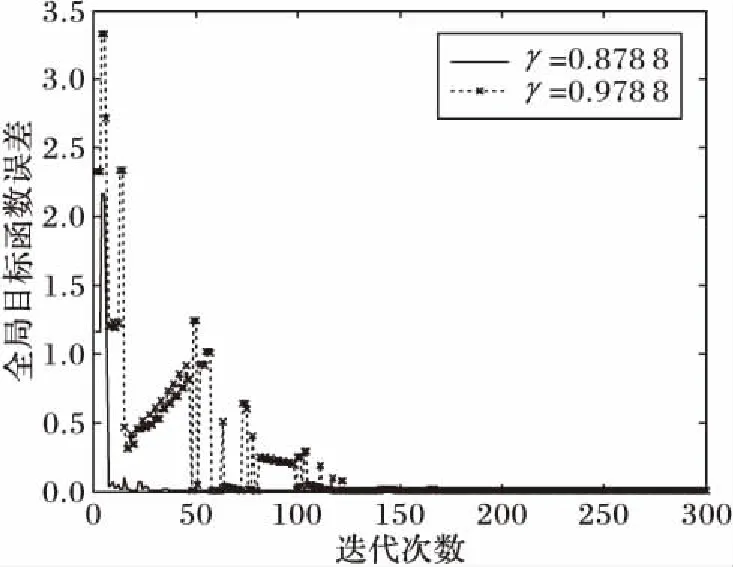
图4　γ=0.978 8及γ=0.878 8时全局目标函数的误差Fig. 4　Global objective function error with γ=0.978 8 and γ=0.878 8

4　结语

在文献[9, 16，21-22]的研究基础上，本文在有向非平衡切换网络中通过设计自适应一致量化器使个体间通过量化信息进行交流，并利用非二次李雅普诺夫函数法刻画了算法的收敛性误差,证明了所提出的量化次梯度优化算法是收敛的，从而可有效避免个体间的交流必须是互惠的以及对带宽是无限的苛刻要求，扩大了算法的适用范围，提高了个体间信息传输速率，更贴合实际应用。

参考文献:

[1]OZDEN S G, SMITH A E, GUE K R. Solving large batches of traveling salesman problems with parallel and distributed computing [J]. Computers & Operations Research, 2017, 85: 87-96.

[2]RAM S S, VEERAVALLI V V, NEDIC A. Distributed and recursive parameter estimation in parametrized linear state-space models [J]. IEEE Transactions on Automatic Control, 2010, 55(2): 488-492.

[3]ZHANG S, ZHANG J, SO H C. Mean square deviation analysis of LMS and NLMS algorithms with white reference inputs [J]. Signal Processing, 2017, 131: 20-26.

[4]SAGHIRI A M, MEYBODI M R. An approach for designing cognitive engines in cognitive peer-to-peer networks [J]. Journal of Network and Computer Applications, 2016, 70: 17-40.

[5]OGBE E, LI X. A new cross decomposition method for stochastic mixed-integer linear programming [J]. European Journal of Operational Research, 2017, 256(2): 487-499.

[6]汪小帆，李翔，陈关荣.网络科学导论[M].北京:高等教育出版社，2012:6. (WANG X F, LI X, CHEN G R. Introduction to Network Science[M]. Beijing: Higher Education Press, 2012: 6.)

[7]CRUZ D, McCLINTOCK J, PERTEET B, et al. Decentralized cooperative control: a multivehicle platform for research in networked embedded systems [J]. IEEE Control Systems Magazine, 2007, 27(3): 58-78.

[8]WANG B, TIAN Y-P. Consensus seeking in second-order multi-agent systems with relative-state-dependent noises [J]. IFAC-Papers Online, 2016, 22(49): 204-209.

[9]LI D, LIU Q, WANG X, et al. Quantized consensus over directed networks with switching topologies [J]. System & Control Letters, 2014, 65: 13-22.

[10]LI D, LIU Q, WANG X, et al. Consensus seeking over directed networks with limited information communication [J]. Automatica, 2013, 49(2): 610-618.

[11]LOBEL I, OZDAGLAR A. Convergence analysis of distributed subgradient methods over random networks [C]// Proceedings of the 2008 46th Annual Allerton Conference on Communication, Control, and Computing. Piscataway, NJ: IEEE, 2008: 353-360.

[12]RAM S S, NEDIC A, VEERAVALLI V V. Incremental stochastic subgradient algorithms for convex optimization [J]. SIAM Journal on Optimization, 2009, 20(2): 691-717.

[14]CARLI R, BULLO F. Quantized coordination algorithms for rendezvous and deployment [J]. SIAM Journal on Control and Optimization， 2009, 48(3): 1251-1274.

[15]CARLI R, FAGNANI F, FRASCA P, et al. Gossip consensus algorithms via quantized communication [J]. Automatica， 2010, 46(1): 70-80.

[16]LI J, CHEN G, WU Z, et al. Distributed subgradient method for multi-agent optimization with quantized communication [J]. Mathematical Methods in the Applied Sciences,2016, 40(4): 1201-1213.

[17]NEDIC A, OZDAGLAR A. TSITSIKLIS J N. Distributed subgradient methods and quantization effects [C]// CDC 2008: Proceedings of the 47th IEEE Conference on Decision and Control. Piscataway, NJ: IEEE, 2008: 4177-4184.

[18]YUAN D, XU S, ZHAO H, et al. Distributed dual averaging method for multi-agent optimization with quantized communication [J]. Systems & Control Letters, 2012, 61(11): 1053-1061.

[19]AYSAL T C, COATES M J, RABBAT M G.Distributed average consensus with dithered quantization [J]. IEEE Transactions on Signal Processing, 2008, 56(10): 4905-4918.

[20]LI T, FU M, XIE L, et al. Distributed consensus with limited communication data rate [J]. IEEE Transactions on Automatic Control, 2011, 56(2): 279-291.

[21]李德权.有向网络多个体系统的量化与鲁棒一致性研究[D].上海:上海交通大学.2012:10. (LI D Q. Quantitative and robust consistency study of multi-individual system with network [D]. Shanghai: Shanghai Jiao Tong University, 2012: 10.)

[22]NEDIC A, OZDAGLAR A. Distributed subgradient methods for multi-agent optimization [J]. IEEE Transactions on Automatic Control, 2009, 54(1): 48-61.

[23]RAMS S S, NEDIC A, VEERAVALLI V V. Distributed stochastic subgradient projection algorithms for convex optimization [J]. Journal of Optimization Theory and Applications, 2011, 147(3): 516-545.

[25]SHI W, LING Q, WU G, et al. A proximal gradient algorithm for decentralized composite optimization [J]. IEEE Transactions on Signal Processing, 2015, 63(22): 6013-6023.