简化的Slope One在线评分预测算法
孙丽梅,李 悦,Ejike Ifeanyi Michael,曹科研
(沈阳建筑大学 信息与控制工程学院,沈阳 110168)(*通信作者电子邮箱limeisun@126.com)
0 引言
在当今大数据时代,各种基于互联网的信息系统普遍存在严重的信息过载问题。推荐系统可以通过对信息进行过滤从而为用户提供个性化的推荐结果,因此已经成为大数据时代信息处理的有效工具。协同过滤算法是推荐系统中最常用的算法之一,它无需像基于内容的推荐算法[1-3]那样考虑内容的表示形式和相似度计算方法,而是主要通过推荐系统中用户的历史行为数据获取用户或项目的偏好特征进行预测,来向用户推荐感兴趣的商品或信息[4]。协同过滤算法通常分为基于记忆(Memory-based)的协同过滤和基于模型(Model-based)的协同过滤,其中基于记忆的协同过滤应用较广,又分为基于用户(User-based)的协同过滤和基于项目(Item-based)的协同过滤[5-7],这类推荐算法先根据历史数据进行训练,然后根据训练结果预测目标用户对项目的评分,最后将评分高的项目推荐给用户。
推荐系统面临的主要问题中,数据稀疏问题一直是影响推荐质量的重要原因之一。推荐系统中,由于每个用户选择的项目数量有限,因此用户对大多数项目的评分为空,导致预测不准确,这就是数据稀疏问题。为了解决数据稀疏问题,一些研究者提出通过基于随机游走[8]、多层最近邻[9]、概率矩阵分解建模[10]等方法先对空评分预测。这些方法虽然在一定程度上提高了推荐精度,但也增加了算法的复杂性,不利于在线推荐。另一些研究者提出通过奇异值分解(Singular Value Decomposition, SVD)减少项目空间维数的方法[11-12],但降维会导致信息损失,在项目空间维数很高时降维的效果难以保证[13]。因此,本文考虑选择实时性较好的在线推荐算法来进一步缓解数据稀疏问题,因为实时性较好的推荐算法可以使新的评分记录迅速补充到历史评分记录中,能有效解决历史评分的数据稀疏问题。
Slope One[14]算法本质上是一种基于项目的协同过滤推荐算法,与其他的基于项目的推荐算法不同,该算法采用项目之间的历史评分差来度量项目之间的相似程度,然后对项目评分进行预测,对稀疏数据有较好的适应性。由于Slope One算法易于实现、预测速度快[15],比传统的Item-based协同过滤算法预测精度高[16],被应用于许多在线推荐系统中,如hitflip DVD推荐系统、Value Investing News 股票新闻网站、AllTheBests 购物推荐引擎等。
虽然Slope One算法比较适合实时在线评分预测,但在训练阶段需要花费大量时间计算任意两个项目的评分差。由于推荐系统的评分表中只保存单个用户对单个项目的评分,计算任意两个项目的评分差相当于数据库中评分表的自连接操作,时间和空间开销极大,因此算法的训练阶段通常需要离线进行。而推荐系统往往应用于数据规模增长迅速、全年不间断运行的大型电子商务系统,在离线训练的间隔内,评分数据仍在迅速增长。
本文在Slope One算法的基础上进一步简化Slope One算法中最耗时的计算评分差的步骤,以项目的历史平均分计算不同项目之间的评分差,进而提出了Simplified Slope One算法。这样一方面可以降低算法的时间复杂度和空间复杂度,使之无需耗时的离线计算,更加适用于需要实时推荐的在线推荐系统;另一方面,简化后的算法不需要两个项目被相同的用户评价过才能计算评分差,任何两个项目只要有历史评分记录就可以计算评分差,有效提高了评分数据的利用率,对稀疏数据有更好的适应性。
本文提出的Simplified Slope One算法预测准确性与原Slope One算法接近,除了保持Slope One算法原有的简单有效特性之外,主要具有以下特点:1)比原Slope One算法更易于实现和维护;2)降低了原Slope One算法的时间复杂度和空间复杂度;3)新增加的评分可以立即用于预测,易于实时在线推荐;4)提高了评分数据利用率,解决推荐系统中的数据稀疏问题。
1 Slope One及其相关算法
推荐系统中,假设有m个用户和n个项目,设用户集合为U={U1,U2,…,Um},项目集合为I={I1,I2,…,In},用户对项目的评分为m×n的矩阵,用R(m,n)表示,其中rij代表用户Ui对项目Ij的评分,评分为0代表未评分。评分矩阵如表1所示。
Slope One算法是一种经典的基于评分预测的算法,采用简单的基于f(x)=x+b形式的线性回归公式进行预测,参数x为目标用户对参照项目的评分,参数b为参照用户对参照项目和目标项目评分的平均差,f(x)即为预测的目标用户对目标项目的评分。其中b是由所有同时评价过这两个项目的参照用户求得评分差之后再求平均得到。实际预测中,会有大量的参照用户和参照项目,因此需要对用户和项目分别加权平均处理。
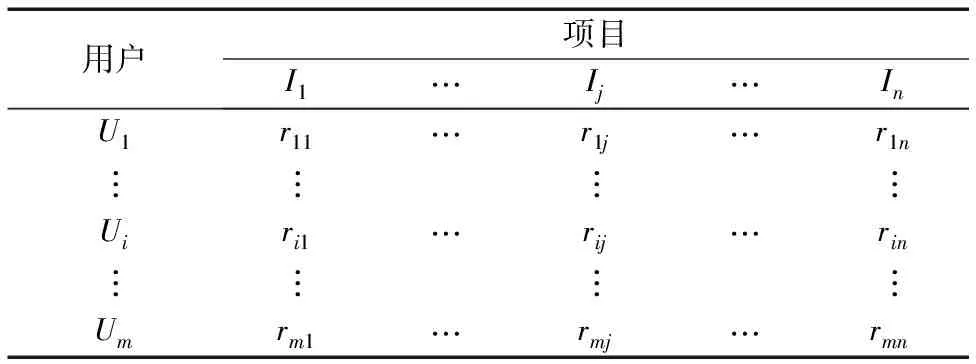
表1 评分矩阵R(m,n)Tab. 1 Rating matrix R(m,n)
图1演示了当只有一个参照用户UserA和一个参照项目Itemi时,如何预测目标用户UserB对目标项目Itemj的评分的方法,“?”代表用户B对项目j的预测评分,计算公式为:
rBj=rBi+(rAj-rAi)
(1)
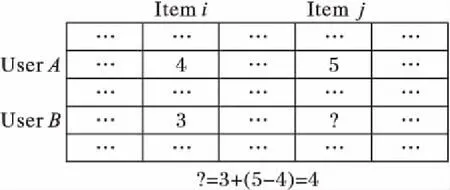
图1 基本Slope One算法示意图Fig. 1 Schematic diagram of basic Slope One algorithm
基本的Slope One预测算法首先采用式(2)计算目标项目与参照物项目的平均评分差devj,k,再采用式(3)预测目标用户u对目标项目的评分P(u)j。
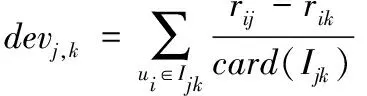
(2)
(3)
其中:Ijk为评价过项目Ij、Ik的参照用户集合;uj表示用户u对项目Ij的评分;Rj为与项目Ij同时被评价过的参照项目集合;card(Rj)代表集合Rj中的参照项目个数。
Slope One算法的作者同时提出了两种改进算法:Weighted Slope One算法和BI-Polar Slope One算法。前者以同时评价过项目Ij、Ik的用户数作为这两个项目评分差的权重;后者以用户平均分作为用户对项目喜欢和不喜欢的判断阈值,将用户对项目的评分分成喜欢评分和不喜欢评分,分别计算喜欢评分差和不喜欢评分差,再加权平均进行预测。
许多研究者在Slope One算法基础上提出了一些改进,如引入SVD进行数据预处理[17],采用动态k近邻[18]、基于用户的协同过滤算法[19-20]对用户进行筛选,采用Pearson相似性计算进行数据处理[21],预先对项目进行聚类处理[22],对用户进行模糊聚类处理[23]等,这些改进虽然可以在一定程度上提高预测评分的准确性,但往往增加了算法的复杂度。因此,本文的研究重点是如何在不影响Slope One算法推荐准确性的前提下尽量降低其时间和空间复杂度。
2 Simplified Slope One算法
2.1 Slope One算法的参照用户和参照项目
Slope One算法中,用户对项目的预测评分可由参照用户对参照项目的评分计算得到。被同一用户评价过的任意两个项目可互为参照项目。在只有较少的参照用户和参照项目时,训练和预测算法都比较简单,但实际推荐时,推荐系统中的参照用户和参照项目都非常多。以Movielens数据集为例,943个用户贡献了10万条评分记录,平均每个用户评价了106个项目,即平均每个项目有105个参照项目。
图2演示了用户C预测项目k时,同时有2个参照用户和2个参照项目时的预测过程。可以看出,预测目标用户对目标项目的评分时,由于参照用户和参照项目各代表一个维度,因此当推荐系统中有m个用户和n个项目时,算法的时间复杂度趋近于O(mn)。
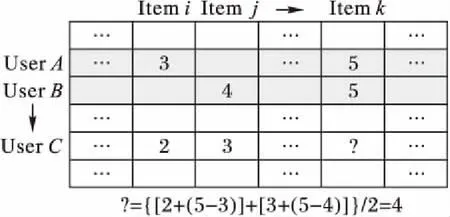
图2 多个参照用户和参照项目的Slope One算法示意图Fig. 2 Schematic diagram of Slope One algorithm with multiple referential users and items
2.2 Simplified Slope One算法
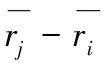
简化后项目i,j的评分差devj,i根据式(4)计算。
(4)
以图3为例,简化后,参照用户A、B…合并为全体用户,用户这个维度的时间复杂度从O(m)降至O(1)。两个项目的平均分之差仍能代表两个项目在评分上的差异。这个简化使原算法中由于参照用户过多而导致的时间和空间复杂度较高的现象得到改善,另外也解决了数据稀疏问题,因为在原Slope One算法中,用户至少贡献2个以上的历史评分才对预测其他评分有参照价值,而简化后的算法中,用户即使只有1个历史评分,也对项目历史平均分有贡献。
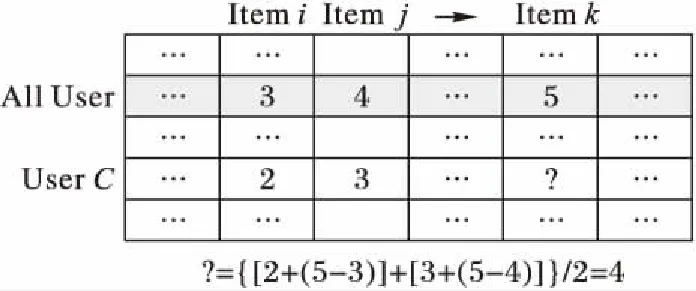
图3 Simplified Slope One算法示意图Fig. 3 Schematic diagram of Simplified Slope One algorithm
相应地,预测目标用户UserC对目标项目Itemj的评分公式变为:
(5)
预测目标用户u对目标项目j的评分p(u)j时,首先找出目标用户评价过的项目作为参照项目集合Rj,再根据式(6)预测评分,其中rui为目标用户u对参照项目i的历史评分。
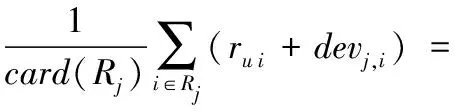
(6)
2.3 时间复杂度和空间复杂度分析
原Slope One算法中,由于预测采用的线性回归模型时间复杂度较低,比较适合实时预测;但与其他推荐算法类似,训练的时间较长,需要离线计算。推荐系统的历史信息中只保存单个用户对单个项目的评分,因此要想得到两个项目的评分差,需要进行复杂的连接操作。评分差简化后的Slope One算法中,较好地降低了算法训练的时间和空间复杂度。
设推荐系统中共有m个用户,n个项目,N个评分。
1)训练阶段时间复杂度对比。
原Slope One算法中,训练阶段的主要计算单位为计算任意两个项目之间的评分差。计算每对项目的评分差共需要n(n-1)/2 个时间单位,时间复杂度为O(n2)。而Simplified Slope One算法中只需要维护n个项目的平均分,因此时间复杂度为O(n)。
2)预测阶段时间复杂度对比。
预测阶段的主要计算单位为查找任意两个项目的评分差。原Slope One算法中,查找每对项目的评分差需要用两个项目id作为关键字进行查找,双关键字查找次数与具体数据库的实现有关,时间复杂度介于O(n)和O(n2)之间。Simplified Slope One算法中,只需要分别查找这两个项目的平均分,然后增加一次减法计算,时间复杂度仍为O(n)。
3)空间复杂度对比。
原Slope One算法中,要存储任意两个项目之间的评分差,需存储2个项目id、总评分次数、总评分差,假设各字段所需单位相同,所需存储空间为4n(n-1)/2=2n(n-1),即空间复杂度为O(n2)。而Simplified Slope One算法中只需要存储n个项目的项目id、总评分次数、总评分,所需空间为3n,因此空间复杂度仍为O(n)。
Simplified Slope One算法在时间复杂度和空间复杂度方面都优于原Slope One算法。
3 实验与结果分析
3.1 时间敏感的Movielens数据集分析
本文采用推荐系统研究中常用的由美国明尼苏达大学GroupLens研究小组提供的Movielens电影评分数据集(10万条评分版本)进行实验。该数据集包含943个用户对1 682部电影的10万条评分记录,评分范围为1~5,每个用户至少评价20部电影,时间跨度约7个月。数据集中的评分记录由用户id、项目id、评分、时间戳组成。MovieLens数据集的数据稀疏度为93.7%,即评分矩阵中有93.7%的评分为空。
MovieLens提供5个子数据集u1~u5,每个子数据集中包含一个训练集和一个测试集,分别是将全部评分记录按80%和20%比例随机选择,用于交叉验证。查询结果显示,这5个子数据集并不是严格按照评价的时间排序的。正常情况下,训练集为历史记录,评分时间应该先于测试集的记录评分时间,但实际的时间戳如表2所示。

表2 Movielens数据集时间戳统计Tab. 2 Timestamp statistics of Movielens dataset
新用户和新项目的冷启动问题是数据稀疏问题的一个特例。实验数据中,如果测试集中的用户在训练集中无评分记录,则视该用户为新用户,反之为非新用户。同理,如果测试集中的项目在训练集中无评分记录,则视该项目为新项目,反之为非新项目。这5个子数据集的测试集中非新用户和非新项目的统计结果如表3所示。
由表3统计结果可知,在这5个子数据集中,测试集中根本不存在新用户,新项目的比例平均为2.2%。以u5为例,整个测试集的20 000条评分记录中,非新用户对非新项目的评分数为19 964,占全部评分记录的99.8%。因此可见,采用Movielens数据集中事先划分好的u1~u5子数据集进行实验时由于新用户和新项目引起的冷启动问题比较少。
在实际应用中,推荐系统的训练集为历史记录,评分时间应先于测试集的记录评分时间。因此,应依据此原则划分数据集,即将全部评分数据先按照时间戳排序后再按比例划分成训练集和测试集,简称时间戳数据集。例如按80%比例划分训练集时,将按照时间戳排序的全部评分记录的前80%作为训练集,后20%作为测试集,这样划分得到的数据集为80%时间戳数据集。表4为分别按50%~90%比例划分训练集时,测试集中的非新用户和非新项目所占比例情况。
由表4可知,按照时间戳划分的测试集中,新用户的比例非常高,平均达到65.1%,新项目平均约为7.8%。同时也可以看出,随着训练集比例的扩大,非新用户和非新项目的比例上升比较明显。

表3 Movielens子数据集中的非新用户和非新项目统计Tab. 3 Statistics of non-new users and non-new items in Movielens subdataset

表4 按时间戳划分数据集中的非新用户和非新项目统计Tab. 4 Statistics of non-new users and non-new items by using timestamp of dataset
Movielens数据集本身已经经过筛选,只保留了评分数在20以上的用户的评分数据,因此,真实的推荐系统中数据稀疏问题和冷启动问题将更加严重。
本文采用推荐系统中常用的平均绝对偏差(Mean Absolute Error, MAE)作为预测评分准确性的度量标准,其计算公式如式(7)所示,MAE值越小越好。其中测试集中的评分数为N,实际用户评分集合为{q1,q2,…,qN},预测得到的评分集合为{p1,p2,…,pN}。
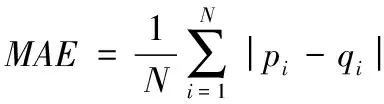
(7)
新用户和新项目在测试集中所占的比例直接影响预测评分的准确性。以常用的基于用户的协同过滤(User-Based Collaborative Filtering, UBCF)推荐算法和Weighted Slope One算法为例,在不按时间戳排序划分的数据集u1~u5上的MAE测试结果比按照时间戳排序取前80%作为训练集划分的数据集(以下简称timestamp80)低13.5%。测试时近邻数k默认设置为10,测试结果如表5所示。
从表5中可看出,测试集中新用户和新项目的比例越高,MAE越大,表明评分预测越不准确,因为只有非新用户和非新项目的历史评分才能贡献预测。而时间戳数据集timestamp80中,数据的稀疏程度远远高于u1~u5子数据集。真实的推荐系统中,历史数据必然先发生于测试数据,也就是说,要模拟真实的推荐系统,应该严格按照时间戳来划分训练集和测试集。因此本文的实验在对MovieLens数据集按照时间戳排序后划分得到的训练集和测试集上进行。

表5 Movielens和timestamp80数据集的平均绝对偏差对比Tab. 5 MAE comparison of Movielens and timestamp80 dataset
3.2 实验及结果分析
将Simplified Slope One算法同改进前的Weighted Slope One算法、BI-Polar Slope One算法以及传统的基于用户的协同过滤算法UBCF(k=10)进行对比实验。实验采用的数据集为Movielens数据集全部943个用户对1 682部电影的10万条评分记录。为了模拟真实的推荐系统环境,所有评分记录严格按照时间戳排序,然后依照训练集比例依次从50%~90%划分出训练集,剩余记录为测试集。实验环境的主要参数如下:Intel Core i7- 4510U CPU;8 GB内存;Windows 8.1(64位)操作系统;MySQL 5.5数据库;jdk1.7开发环境;Java语言。
表6所示为随机抽取500个用户,按50%比例划分训练集和测试集时,各算法的训练时间和数据存储空间的对比。可以看出,由于推荐系统中的项目数比用户数大得多,因此基于项目的Weighted Slope One和BI-polar Slope One算法的训练时间和存储空间都远远大于基于用户的UBCF算法;而本文提出的Simplified Slope One算法虽然也是基于项目的推荐算法,但由于简化后降低了时间复杂度和空间复杂度,因此,其训练时间和数据存储空间均远远小于其他算法。

表6 训练时间和数据存储空间对比Tab. 6 Comparison of training time and data storage space
图4、5为各算法预测评分准确性的测试结果,通过计算推荐算法对测试数据集中用户的预测评分与其实际评分之间的平均差来度量预测评分的准确性,采用的准确性度量指标为平均绝对偏差MAE。其中图4为随机抽取500个用户的结果,图5则为采用全部943个用户的结果。
从图4、5中可以看出,在严格按照时间戳排序后划分的数据集中,MAE整体偏高,这是由于新用户和新项目所占比例较高,数据较稀疏。但本文提出的Simplified Slope One算法与原来的Weighted Slope One算法的MAE几乎重合,图5中,仅在训练集比例超过80%之后略高于Weighted Slope One算法,而通常推荐系统中训练集在全部数据中所占比例都小于80%,这表明本文提出的Simplified Slope One算法虽然简化了原算法的计算评分差过程,但对预测评分的准确性影响较小,而且无论时间复杂度还是空间复杂度都降低至仅为O(n),远优于Weighted Slope One算法和BI-polar Slope One算法,因此,Simplified Slope One算法能更好地适应数据规模增长迅速的推荐系统。
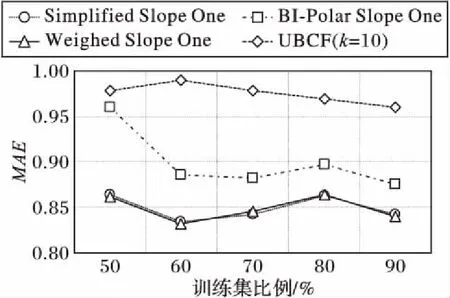
图4 算法的MAE对比(随机选取500个用户)Fig. 4 MAE Comparison among algorithms (500 randomly selected users)
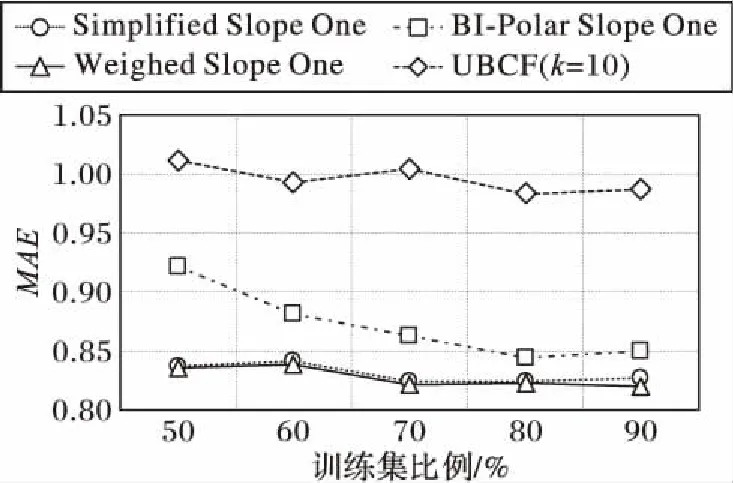
图5 算法的MAE对比(采用全部943个用户)Fig. 5 MAE Comparison among algorithms (all 943 users)
4 结语
本文提出了Simplified Slope One算法,以项目的历史平均评分之差代替原Slope One算法中相同用户同时评价两项目得到的评分差。由于推荐系统中只保存单个用户对单个项目的评分,因此原算法中需要执行耗时的表连接操作才能得到任意两项目的评分差,而简化后的Simplified Slope One算法将时间复杂度和空间复杂度均降低至O(n)。此外,Simplified Slope One算法不需要用户同时评价两个项目才能计算评分差,使任何两个项目只要有历史评分记录就可以计算评分差,因而有效提高了评分数据的利用率。Simplified Slope One算法减少了训练时间以后,可以缩短训练周期,使新的评分记录迅速补充到历史记录中,对后面的预测起到训练作用,有效地解决了测试集中的数据稀疏问题。在按照时间戳排序后划分的Movielens数据集上的测试结果表明,Simplified Slope One算法对评分预测的准确性与原 Slope One算法非常接近,但时间复杂度和空间复杂度均优于原Slope One算法,因此更适合在数据规模增长迅速的大型推荐系统中应用。
参考文献:
[1]LOPS P, de GEMMIS M, SEMERARO G, et al. Content-based and collaborative techniques for tag recommendation: an empirical evaluation [J]. Journal of Intelligent Information Systems, 2013, 40(1): 41-61.
[2]FENG S, CAO J, WANG J, et al. Recommendations based on comprehensively exploiting the latent factors hidden in items’ ratings and content [J]. ACM Transactions on Knowledge Discovery from Data, 2017, 11(3): Article No. 35.
[3]GEORGIOU T, EL ABBADI A, YAN X. Extracting topics with focused communities for social content recommendation [C]// Proceedings of the 2017 ACM Conference on Computer Supported Cooperative Work and Social Computing. New York: ACM, 2017: 1432-1443.
[4]ALEXANDRIDIS G, SIOLAS G, STAFYLOPATIS A. Enhancing social collaborative filtering through the application of non-negative matrix factorization and exponential random graph models [J]. Data Mining & Knowledge Discovery, 2017, 31(4): 1031-1059.
[5]WANG J, DE VRIES A P, REINDERS M J T. Unifying user-based and item-based collaborative filtering approaches by similarity fusion [C]// SIGIR 2006: Proceedings of the 29th Annual International ACM SIGIR Conference on Research and Development in Information Retrieval. New York: ACM, 2006: 501-508.
[6]SARWAR B, KARYPIS G, KONSTAN J, et al. Item-based collaborative filtering recommendation algorithms [C]// WWW ’01: Proceedings of the 10th International Conference on World Wide Web. New York: ACM, 2001: 285-295.
[7]JAMALI M, ESTER M. Trustwalker: a random walk model for combining trust-based and item-based recommendation [C]// KDD ’09: Proceedings of the 15th ACM SIGKDD International Conference on Knowledge Discovery and Data Mining. New York: ACM, 2009: 397-406.
[8]YILDIRIM H, KRISHNAMOORTHY M S. A random walk method for alleviating the sparsity problem in collaborative filtering [C]// RecSys ’08: Proceedings of the 2008 ACM Conference on Recommender Systems. New York: ACM, 2008: 131-138.
[9]YIN F. Sparsity-tolerated algorithm with missing value recovering in user-based collaborative filtering recommendation [J]. Journal of Information & Computational Science, 2013, 10(15): 4939-4948.
[10]REN X, SONG M, HAIHONG E, et al. Context-aware probabilistic matrix factorization modeling for point-of-interest recommendation [J]. Neurocomputing, 2017, 241: 38-55.
[11]SARWAR B M, KARYPIS G, KONSTAN J A, et al. Application of dimensionality reduction in recommender system — a case study [C]// Proceedings of the 2000 ACM WebKDD Web Mining for E-Commerce Workshop. New York: ACM, 2000: 82-90.
[12]柴华,刘建毅.一种改进的Slope One推荐算法研究[J].信息网络安全,2015(2):77-81. (CHAI H, LIU J Y. Research on improved Slope One recommendation algorithm [J]. Netinfo Security, 2015(2): 77-81.)
[13]孙丽梅,李晶皎,孙焕良.基于动态k近邻的Slope One协同过滤推荐算法[J].计算机科学与探索,2011,5(9):857-864. (SUN L M, LI J J, SUN H L. Slope One collaborative filtering recommendation algorithm based on dynamick-nearest-neighborhood [J]. Journal of Frontiers of Computer Science and Technology, 2011, 5(9): 857-864.)
[14]LEMIRE D, MACLACHLAN A. Slope One predictors for online rating-based collaborative filtering [C]// SDM ’05: Proceedings of the 2005 SIAM Data Mining Conference. Philadelphia, PA: Society for Industrial and Applied Mathematics (SIAM), 2005: 471-475.
[15]JANNACH D, ZANKER M, FELFERNIG A, et al.推荐系统[M].蒋凡,译.北京:人民邮电出版社,2013:26-28. (JANNACH D, ZANKER M, FELFERNIG A, et al. Recommender Systems [M]. JIANG F, translated. Beijing: Posts & Telecom Press, 2013: 26-28.)
[16]董丽,邢春晓,王克宏.基于不同数据集的协作过滤算法评测[J].清华大学学报(自然科学版),2009,49(4):590-594. (DONG L, XING C X, WANG K H. Collaborative filtering algorithm evaluation for various datasets [J]. Journal of Tsinghua University (Science and Technology), 2009, 49(4): 590-594.)
[17]LIU Y, LIU D, XIE H, et al. A research on the improved Slope One algorithm for collaborative filtering [J]. International Journal of Computing Science & Mathematics, 2016, 7(3): 245-253.
[18]LI J, SUN L, WANG J. A Slope One collaborative filtering recommendation algorithm using uncertain neighbors optimizing [C]// WAIM 2011: Proceedings of the 2011 International Conference on Web-Age Information Management, LNCS 7142. Berlin: Springer, 2011: 160-166.
[19]TIAN S, OU L. An improved Slope One algorithm combining KNN method weighted by user similarity [C]// WAIM 2016: Proceedings of the 2016 International Conference on Web-Age Information Management, LNCS 9998. Cham: Springer, 2016: 88-98.
[20]王潘潘,钱谦,王锋.改进加权Slope One协同过滤推荐算法研究[J].传感器与微系统,2017,36(7):138-141. (WANG P P, QIAN Q, WANG F. Study on improved weighted Slope one collaborative filtering algorithm [J]. Transducer and Microsystem Technologies, 2017, 36(7): 138-141.)
[21]VADIVELOU G, ILAVARASAN E. Fusion of Pearson similarity and Slope One methods for QoS prediction for Web services [C]// IC3I 2015: Proceedings of the 2014 International Conference on Contemporary Computing and Informatics. Piscataway, NJ: IEEE, 2014: 1118-1124.
[22]MI Z, XU C. A recommendation algorithm combining clustering method and Slope One scheme [C]// ICIC 2011: Proceedings of the 2011 Bio-Inspired Computing and Applications — International Conference on Intelligent Computing, LNCS 6840. Berlin: Springer, 2011: 160-167.
[23]LIANG T, FAN J, ZHAO J, et al. Improved Slope One collaborative filtering predictor using fuzzy clustering [C]// ADMA 2013: Proceedings of the 2013 International Conference on Advanced Data Mining and Applications, LNCS 8346. Berlin: Springer, 2013: 181-192.

