基于k-核过滤的社交网络影响最大化算法
李阅志,祝园园,钟 鸣
(1.软件工程国家重点实验室(武汉大学),武汉 430072; 2.武汉大学 计算机学院,武汉 430072)(*通信作者电子邮箱yyzhu@whu.edu.cn)
0 引言
随着Facebook和微信微博等社交网络的流行,越来越多的用户喜欢在社交网络中分享自己的观点和其他信息,使得网络影响力传播的研究成为社交网络分析的热点[1]。 影响力最大化问题作为病毒式营销和广告投放等社交网络推荐研究领域的一个重要问题,引起了广泛的关注和研究热情。
影响最大化问题最早由Domingos等[2]定义为如何寻找t个初始节点,使得信息的最终传播范围最广。 Kempe等[3]将影响最大化定义为一个离散优化问题,证实了这个问题在独立级联模型下是NP难问题,提出了对后续研究影响极大的两种传播模型:独立级联(Independent Cascade,IC)模型和线性阈值(Linear Threshhold,LT)模型,并基于子模性质(sub-modularity)提出了一个基本的贪心算法Greedy。 为了降低Greedy算法的时间复杂度,后来的研究者又提出了若干改进算法,如CELF(Cost-Effective Lazy Forward)算法[4]、DegreeDiscount算法[5]、核覆盖算法(Core Covering Algorithm, CCA)[6]、PMIA(Prefix excluding Maximum Influence Arborescence)算法[7]、IRIE(Influence Rank Influence Estimation)算法[8]等。 其中PMIA算法和IRIE算法被认为是现有影响力最大化算法中影响范围和时间效率排名靠前的算法。这些算法基本都使用了子模性质,虽然时间效率有了很大的提升,但是影响范围效果仍然比不上Greedy算法[3]。
Kempe等[3]已经证明具有子模性的影响范围函数使用Greedy算法求解,能取得最优解的63%[9]。该结论表明当前取得最大影响范围的Greedy算法和最优解仍有差距。 为了缩小现有影响最大化算法和最优解的差距,本文提出一种采用k-核过滤的算法,可以应用于现有的大多数基于子模性质的影响最大化算法,扩大它们的影响范围,降低它们的时间复杂度。基于该k-核过滤算法,本文对PMIA算法、CCA、OutDegree算法、Random算法分别进行优化,扩大了影响范围, 降低了执行时间,尤其对于CCA,在不减小影响范围的情况下执行时间缩短了28.5%。并且通过预训练k首次发现同一算法在同一数据集上取得最佳优化效果的k是固定值。李国良等[10]提出了一种针对多网络实体影响最大化的算法,本文将k-核过滤算法结合该算法思想应用到单个社交网络上,提出了一种新的影响最大化算法GIMS(General Influence Maximization in Social networks),该算法比PMIA和IRIE的影响范围更大,执行时间更短。
1 传播模型和问题定义
设有向图G=(V,E)表示一个社交网络,其中:V表示节点集合,n表示节点总数;E表示边集,m表示边的总数。∀v∈V表示节点,∀e(u,v)∈E表示一条u指向v的有向边。
1.1 独立级联模型
独立级联模型是一个概率模型。对于网络G中的每个节点都有两个状态:激活和未激活。每个节点只能从未激活状态转变为激活状态,每个节点可以被它的相邻节点激活。对于每条边e(u,v)∈E,需指定一个影响概率p(u,v)∈[0,1],p(u,v)表示节点u通过边e(u,v)影响节点v的概率。给定初始激活节点集合S0,传播过程以如下方式进行:当传播至第t+1步时,利用在第t步中被激活的节点,根据成功概率p(u,v)试图去激活它们的邻居节点,并将在这一步中被激活的节点加入到St形成St+1;重复这一过程,直至不再有新的节点被激活。整个过程中u只尝试激活v一次,激活成功则v由未激活变为激活状态,激活失败则不再尝试激活。
1.2 问题定义
定义1有向图G=(V,E)中,给定一个输入t,独立级联模型下的影响最大化(Influence Maximization, IM)问题是找到G一个节点子集S*∈V,S*的最终影响范围σ(S*)满足:
σ(S*)=max{σ(S)||S|=t,S⊆V}
s.t.|S*|=t
定义2一个集合函数f:2V→R是单调的,如果f(S)≤f(T)对所有S⊆T都成立。
定义3一个集合函数f:2V→R是子模的,如果f(S∪{u})-f(S)≥f(T∪{u})-f(T)对所有S⊆T⊆V和u∈V都成立。
Kempe等[3]证明了影响最大化问题是NP难问题,并且证明影响范围函数满足单调性和子模性,由此提出了可获得(1-1/e)的近似最优解Greedy算法。Greedy算法的影响范围是现有影响最大化算法中效果最好的,能取得最优解的63%[3],但时间效率很低,执行一次需要几个小时甚至几天。本文提出一种k-核过滤算法,可以扩大现有算法的影响范围,并且降低算法的执行时间复杂度。
2 基于k-核过滤的影响最大化算法
本文提出了一种k-核过滤算法,可以应用于很多影响最大化算法,扩大它们的影响范围,缩短其执行时间。同时,本文还提出了一种新的单社交网络影响最大化算法GIMS,其影响范围比广泛认可的PMIA算法和IRIE算法效果更好,执行时间比PMIA算法更少。
2.1 k-核
定义4集合Vk⊆V的任一节点v的度数不少于k,由Vk所推导出的最大诱导子图Gk(Vk,Ek)称为k-核。
k-核概念由Seidman[11]于1983年提出,可用来描述度分布所不能描述的网络特征,揭示源于系统特殊结构的结构性质和层次性质。虽然节点度在影响最大化问题中被研究者广泛关注,但是度较大的节点可能较为分散,而k-核使得度较大的节点聚集起来,网络分布越集中,就越能受到彼此影响,从而产生更大的网络影响力。因此本文采用k-核来优化现有影响最大化算法。
2.2 k-核过滤算法
本文提出的k-核过滤算法不是一个独立的影响最大化算法,而是通过与现有影响最大化算法相结合来扩大现有算法的影响范围,并缩短其执行时间。k-核过滤算法的基本思想是通过预训练k,找到对现有算法具有最佳优化效果、并且与选择种子节点数t无关的固定k值,在给定需要选择的节点数t时,通过计算图的k-核过滤不属于k-核子图的节点和边,在k-核子图上执行现有影响最大化算法,从而达到减少计算量的目的。
k-核过滤算法涉及两个步骤:1)通过预先训练找到能产生优化效果最好的参数k,如算法1所示;2)计算网络的k-核,并应用在现有算法中,如算法2所示。
算法1预训练k。
输入有向图G=(V,E), 迭代次数iter;
输出最佳优化效果k。
1)
optk=0,k=0,t=rand(0, 10),σopt=0;
2)
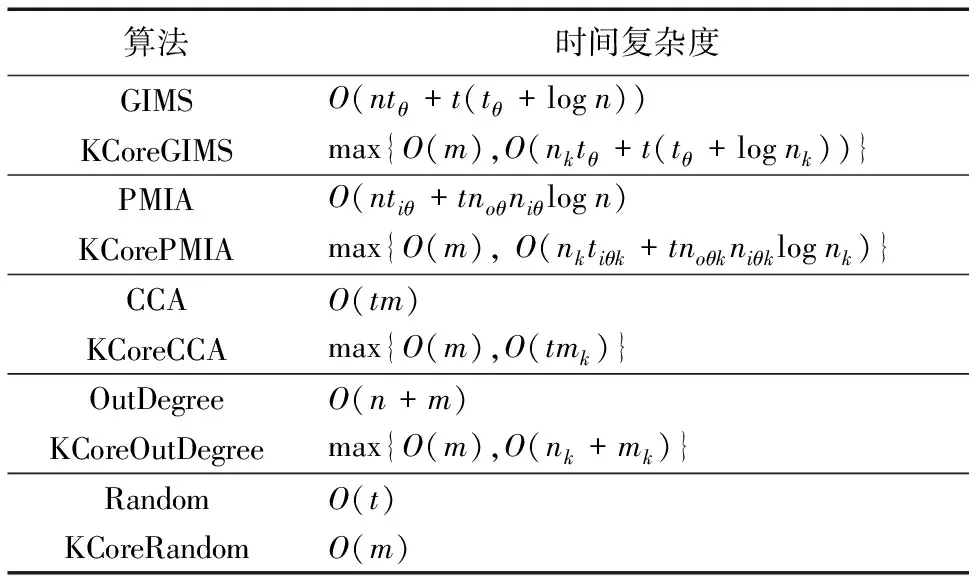
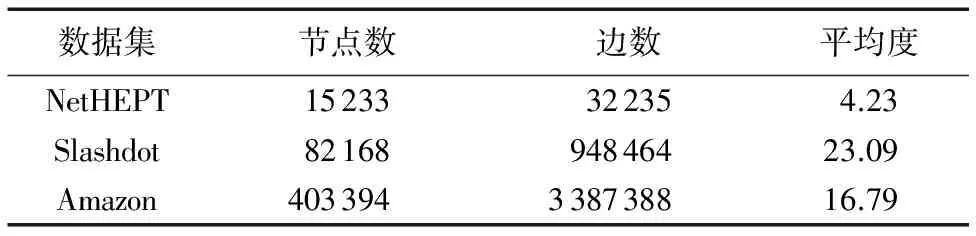
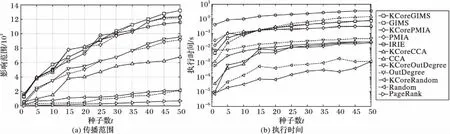
whilek 3) computeGk, thek-core subgraph ofG; 4) imply existing IM algorithm onGk; 5) ifσk>σopt 6) optk=k;σopt=σk; 7) k++; 8) returnoptk; 算法2k-核优化现有算法。 输入有向图G=(V,E), 最佳优化效果k,种子节点数t; 输出种子集合S。 1) computeGk, thek-core subgraph ofG; 2) S=existing IM algorithm onGk; 3) returnS; 算法1的预训练过程需要提前完成以选出最佳优化效果k,由本文实验可知,在选取不同的种子个数t时,取得最佳优化效果的k是固定值。接着采用算法2计算G的种子集合S,此时的执行时间会减少很多,影响范围效果也会更好。本文利用Batagelj等[12]提出的算法计算k-核子图Gk,通过迭代删除度小于k的所有顶点和与之相连的边,剩下的子图就是k-核,时间复杂度为O(m)。针对不同的现有算法,k-核过滤算法有不同的结合方式,算法的时间复杂度取决于现有算法的时间复杂度,但通常比结合前的原算法效率更高。假设现有算法的时间复杂度为f(n,m),那么k-核过滤算法的时间复杂度为max{O(m),f(nk,mk)},其中nk和mk表示k-核子图的节点数和边数。通常f(n,m)都是大于O(m)的复杂度,通过k-核过滤之后算法时间复杂度不超过O(m)和f(nk,mk)的最大值,但一定小于f(n,m)。算法2也可以脱离算法1直接执行,可以任意选择k,对现有算法的影响范围和执行时间都会有改进,只是没有预训练k的优化效果好。 现有影响最大化算法中,PMIA算法和IRIE算法传播影响效果较好,其中PMIA的内存耗费较大,IRIE算法执行时间较长。本文将k-核过滤算法分别与CCA[6]、PMIA算法[7]、OutDegree算法[1]和Random算法相结合,得到KCoreCCA算法、KCorePMIA算法、KCoreOutDegree算法和KCoreRandom算法,以扩大原算法的影响范围,缩短其执行时间。IRIE算法[8]和PageRank算法[13]是基于节点排名的算法,节点排名依赖于整个网络所有节点的收敛,k-核过滤算法原理是先剪枝不重要的节点,因此无法应用在这两个算法中。 2.3.1KCoreCCA 核覆盖算法(CCA)是基于覆盖距离选择核数最大的t个节点作为种子节点。核数k表示节点属于k-核,而不属于(k+1)-核。CCA和k-核过滤算法都是基于k-核的概念提出的,较小核数的节点对CCA毫无贡献,剪枝核数较小的节点虽然对CCA的影响范围没有改变,但是可以大大缩短CCA的执行时间。 算法3KCoreCCA。 输入有向图G(V,E),种子节点数t, 覆盖距离d; 输出种子集合S。 1) initializeS=∅; 2) computeGk(Vk,Ek), thek-core subgraph ofG; 3) computeCores(Gk); 4) foreach vertexv∈Vkdo 5) COv=false; 6) fori=1 totdo 7) 8) 9) S=S∪{u}; 10) foreach vertexvin {v|du,v≤d,v∈Vk} do 11) COv=true; 12) returnS; 其中:Cv为节点的核数,COv表示节点覆盖属性,du,v表示节点u和v之间的距离。算法3是将k-核过滤算法应用于CCA,CCA的时间复杂度是O(tm)[6]。KCoreCCA先计算出k-核子图(第2)行),时间复杂度是O(m);第3)~12)行遵循CCA的基本思路,但只针对k-核计算,而不是整个网络,时间复杂度是O(tmk)。所以 KCoreCCA的时间复杂度是max{O(m),O(tmk)},因为剪枝了很多节点,减少了计算量。 KCoreCCA是以核数考量选择种子节点,而以出度考量选取种子节点的算法,称为OutDegree算法,类似优化CCA的方式,应用k-核过滤算法于OutDegree算法,得到KCoreOutDegree算法,OutDegree算法时间复杂度为O(n+m),KCoreOutDegree算法时间复杂度为max{O(m),O(nk,mk)}。k-核过滤算法应用于随机选取种子节点的Random算法,得到KCoreRandom算法,Random算法时间复杂度为O(t),KCoreRandom算法时间复杂度为max{O(m),O(t)}=O(m)。 2.3.2KCorePMIA算法 PMIA算法先计算每个节点∀v∈V的本地树结构PMIIA和PMIOA,基于本地树结构PMIIA计算当前种子集合S对每个节点u的影响ap(u,S,PMIIA(v,θ)),并根据影响线性(Influence Linearity)性质计算影响系数α(v,u),然后根据本地树结构结合子模性选出影响最大的t个节点。PMIA算法需计算每个节点的本地树结构,虽然加快了影响传播的计算和更新,但保存每个节点的本地树结构需要耗费大量内存,计算全部节点本地树结构效率也较低。本文采用k-核过滤算法筛选出可能是最具影响力的节点,只需计算这些节点的本地树结构,从而减少了大量计算。 算法4KCorePMIA算法。 输入有向图G(V,E), 种子节点数t,路径传播阈值θ; 输出种子集合S。 1) setS=∅; 2) setIncInf(v)=0 for each nodev∈V 3) computeGk(Vk,Ek), thek-core subgraph ofG; 4) foreach vertexv∈Gkdo 5) compute PMIIA(v,θ,S); 6) set ap(u,S,PMIIA(v,θ,S))=0,∀u∈PMIIA(v,θ,S); 7) computeα(v,u),∀u∈PMIIA(v,θ,S) 8) foreach vertexu∈PMIIA(v,θ,S) do 9) IncInf(u)+= α(v,u)*(1-ap(u,S,PMIIA(v,θ,S))); 10) fori=1 totdo 11) 12) compute PMIOA(u,θ,S); 13) foreachv∈PMIOA(u,θ,S)∩Vkdo 14) forw∈PMIIA(v,θ,S)Sdo 15) IncInf(w)-= α(v,w)*(1-ap(w,S,PMIIA(v,θ,S))); 16) S=S∪{u}; 17) forv∈PMIOA(u,θ,S{u}){u}∩Vkdo 18) compute PMIIA(v,θ,S); 19) computeap(w,S,PMIIA(v,θ,S)),∀w∈PMIIA(v,θ,S) 20) computeα(v,w),∀w∈PMIIA(v,θ,S) 21) forw∈PMIIA(v,θ,S)Sdo 22) IncInf(w)-= α(v,w)*(1-ap(w,S,PMIIA(v,θ,S))); 23) returnS; PMIA算法的时间复杂度是O(ntiθ+tnoθniθlogn),其中niθ和noθ分别是所有节点的PMIIA本地树结构和PMIOA本地树结构的最大节点数,tiθ是计算所有节点的PMIIA本地树结构的最长时间[7],由于每个节点都需要计算PMIIA和PMIOA子树结构,PMIA算法的时间复杂度一定大于O(m)。而KCorePMIA算法先计算k-核子图Gk(第3)行),时间复杂度是O(m),过滤掉部分节点后,只需在Gk上再执行PMIA算法(第4)~23)行),时间复杂度是O(nktiθk+tnoθkniθklognk),因此KCorePMIA算法的时间复杂度为max{O(m),O(nktiθk+tnoθkniθklognk)}。当k较大时,nk远小于n,KCorePMIA算法的时间复杂度不大于O(m)。 李国良等[10]提出的BoundBasedIMMS(BoundBased Influence Maximization in Multiple Social networks)算法可以有效解决存在实体对应关系的多网络影响最大化问题,本文对该算法进行扩展,以设计一种可以有效解决单个社交网络上的影响最大化问题的算法GIMS。GIMS扩展了基于树的算法模型[7],结合独立级联模型的单调性和子模性,降低了时间复杂度,同时也保证了影响范围效果。 路径Pu,v=(n1=u,n2,…,nm=v)表示经由节点u到节点v的一条路径。在独立级联模型下,节点u沿路径P激活节点v的概率为: 节点u可以通过多条路径影响到节点v,为减少计算量,采用最大影响路径MPP(u,v)来近似节点u对节点v的影响概率: pp(u,v)≈pp(MPP(u,v))=pp(arg max(pp(Pu,v))) 通过计算所有节点到节点u的影响概率,可以构建最大逆向传播树ITree(u),考虑到当pp(u,v)小于某一个阈值θ时,节点v被u激活的概率较小,则忽略此节点。同理,计算节点u到所有其他节点的影响概率,可以构建最大传播树Otree(u)。 给定激活的种子集合S,假设S中的每个节点独立地影响其他未激活的节点,并且只在已构建的传播树中传播影响,则S对未激活节点v的影响概率为: 在种子集合S中加入一个新激活的节点u后,种子集合对节点v的影响增益gain(u|S,v)为: gain(u|S,v)=pp(S∪{u},v)-pp(S,v)= 假设每个节点都是独立影响其他节点,那么种子集合S中新增加一个激活节点u后总的影响增益gain(u|S)为: 根据影响最大化问题的子模性,每次选取影响增益gain(u|S)最大的节点加入种子集合S中,直到选取t个节点。 算法5GIMS算法。 输入有向图G(V,E), 种子节点数t,路径传播阈值θ; 输出种子集合S。 1) precomputeITree(v) andOTree(v) withθ, for ∀v∈V; 2) initialize big heapHof Node {v.id,v.spread,v.status}, for ∀v∈V; 3) setS=∅; 4) initializepp(S,v)=0, for ∀v∈V; 5) fori=1 totdo 6) Nodetnode=H.top(); 7) while(tnode.status!=i) do 8) computegain(tnode.id|S); 9) tnode.spread=gain(tnode.id|S); 10) tnode.status=i; 11) H.sort(); 12) tnode=H.top(); 13) tnode=H.pop(); 14) S=S∪{tnode.id}; 15) updatepp(S,v), for ∀v∈V; 16) H.sort(); 17) returnS; 算法5通过构造树模型近似计算传播概率(第1)行),时间复杂度是O(ntθ),其中tθ是所有ITree(v)和OTree(v)的最大顶点数。然后依据独立影响假设简化了影响增益计算,构造大根堆避免了很多影响力小的节点的计算(第6)~16)行)。每次计算gain(tnode.id|S)的时间复杂度是O(tθ),调整堆H的时间复杂度是O(logn),每次迭代更新常量次节点status即可选出最优tnode,所以第6)~16)行的时间复杂度是O(tθ+logn)。因此GIMS的时间复杂度为O(ntθ+t(tθ+logn))。在此基础上,本文应用k-核优化GIMS算法,称为KCoreGIMS算法。KCoreGIMS算法先通过计算k-核剪枝部分影响力小的节点,时间复杂度为O(m),在计算算法5的第1)行和第2)行时无需计算全部网络节点,而只需在k-核子图上执行GIMS算法从而减少计算量,时间复杂度为O(nktθ+t(tθ+lognk))。因此KCoreGIMS的算法时间复杂度为max{O(m),O(nktθ+t(tθ+lognk))}。 经过2.4节对各算法分析,总结各算法和其k-核过滤算法的时间复杂度如表1。可以看到,对于影响范围效果好的算法GIMS、PMIA、CCA、OutDegree,计算k-核的时间复杂度是O(m),但执行现有影响最大化算法时由于只需要考虑k-核子图的节点和边,使得原算法的复杂度有所降低。对于效果较差的Random算法,由于是随机选择种子节点,使用k-核过滤时计算k-核使时间复杂度有所增加。因此,对于一般影响最大化算法而言,k-核过滤算法使得原算法的时间复杂度有所降低。 表1 不同影响最大化算法及其k-核过滤算法的时间复杂度比较Tab. 1 Time complexity comparison of different IM algorithms and their k-core filtered versions 本文实验在三个真实数据集上进行,分别是ArXiv(https://arxiv.org/)物理领域作者合作关系网络NetHEPT(collaboration Network of High Energy Physics Theory from arXiv.org)、社交网络Slashdot和商品团购网络Amazon(http://snap.stanford.edu/data/index.html)。这三个数据集的统计特性如表2所示。 表2 实验中的数据集Tab. 2 Experimental datasets 本文实验比较了GIMS算法、PMIA算法、IRIE算法、CCA、OutDegree算法、PageRank算法和Random算法,以及 它们的k-核过滤算法。其中IRIE算法和PageRank由于依赖全局节点排名不适合k-核过滤;CCA的覆盖距离d设置为2;GIMS算法、PMIA算法传播概率阈值θ设置为1/320;社交网络中节点u到节点v的传播概率初始化为1/InDeg(v),其中InDeg(v)表示节点v的入度。由于模型的随机性,在计算选择的t个节点的影响范围时采用蒙特卡罗重复模拟10 000次,取平均值。 所有程序代码都是基于C++语言编程,计算机配置为:centos 6.6, Intel Xeon CPU E5- 2640 v3 2.60 GHz,8 GB内存。 为了评估k-核过滤算法对现有算法的优化效果,本文定义两个评估指标,影响范围优化百分比influ_opt和执行时间优化百分比time_opt。假设A算法的k-核过滤算法是KCoreA,当选择t个种子节点时,算法KCoreA的影响范围和执行时间分别是kcore_influ和kcore_time,算法A的影响范围和执行时间分别是influ和time,那么: influ_opt=(kcore_influ-influ)/influ time_opt=(time-kcore_time)/time 当种子节点数1≤t≤50时,定义平均影响范围优化百分比avg_influ_opt和平均执行时间优化百分比avg_time_opt分别为所有t值下influ_opt和time_opt的平均值。 图1(a)、(b)分别是NetHEPT上各个算法及其k-核过滤算法的传播范围和执行时间。通过算法1的预训练k发现选取不同种子个数时取得最佳优化效果的k是固定值:KCoreGIMS最佳优化效果k为3或4,KCorePMIA的最优k为1或2,KCoreCCA的最优k为8,KCoreOutDegree的最优k为3,KCoreRandom的最优k为4或5。从图1可以看到,本文提出的GIMS算法及其优化算法KCoreGIMS比现有算法中效果较好的PMIA算法和IRIE算法选出的节点传播效果更好,执行时间保持在毫秒级别,比IRIE算法更有效率。k-核过滤对于不同算法的优化效果不同。对算法本身效果较优的GIMS算法、PMIA算法来说,k-核优化效果比原算法的影响范围扩大了1%左右;对OutDegree算法和Random算法影响范围扩大了10%以上;对CCA传播范围没有影响,但是执行时间缩短了27%。也即,对所有算法影响范围都扩大了,执行时间都缩短了。 图1 NetHEPT数据集上的传播范围和执行时间Fig. 1 Influence range and execution time on NetHEPT dataset 图2(a)、(b)分别是Slashdot数据集上各个算法及其k-核过滤算法的传播范围和执行时间。通过算法1的预训练k发现选取不同种子个数时取得最佳优化效果的k是固定值:KCoreGIMS的最优k为22或44,KCorePMIA的最优k为5或6,KCoreCCA的最优k为50,KCoreOutDegree的最优k为40或50,KCoreRandom的最优k为42或44。从图2可以看到,本文提出的GIMS算法及其优化算法KCoreGIMS仍然是传播范围最好的算法,比PMIA算法和IRIE算法高出2 000多节点,执行时间远少于IRIE算法和PMIA算法。k-核过滤算法对GIMS算法和PMIA算法影响范围扩大了2%以上,执行时间缩短了2%以上,对CCA和OutDegree算法执行时间缩短了27%左右。 图3(a)、(b)是Amazon数据集上各算法及其k-核过滤算法的影响范围和执行时间。通过算法1的预训练k发现选取 不同种子个数时取得最佳优化效果的k是固定值:GIMS的最优k为11,KCorePMIA的最优k为10,KCoreCCA的最优k为19,KCoreOutDegree的最优k为5或7,KCoreRandom的最优k为3或6。从图3可以看到,本文提出的GIMS及其优化算法KCoreGIMS仍是影响范围最大的算法,执行时间也远低于IRIE算法。K-核过滤算法对GIMS算法和PMIA算法影响范围扩大了1%以上,对OutDegree算法影响范围扩大了21%以上,对CCA的执行时间缩短了28%左右。 图2 Slashdot数据集上的传播范围和执行时间Fig. 2 Influence range and execution time on Slashdot dataset 图3 Amazon数据集上的传播范围和执行时间Fig. 3 Influence range and execution time on Amazon dataset 从图性质来看,Amazon是稀疏的大网络,Slashdot和NetHEPT是稠密的小网络,但GIMS和KCoreGIMS保持了更大的影响范围和有竞争力的执行时间,k-核过滤算法对各算法的影响范围和执行效率都有不错的优化效果。这说明了GIMS算法和k-核过滤算法的鲁棒性。为了更好地展示k-核过滤算法对各算法的影响范围和执行效率的优化效果,表3给出了各算法的平均影响范围和执行时间优化百分比,也就是定义在3.2节的avg_influ_opt和avg_time_opt。 从表3可以看到,k-核过滤算法对GIMS算法和PMIA算法的优化效果较弱,但是也有提高;对CCA的影响范围没有扩大,但是大大缩短了CCA的执行时间;对OutDegree算法和Random算法扩大了影响范围,缩短了执行时间。 通过对图1~3和表3的综合分析可以得出以下结论:1)本文提出的GIMS算法及其k-核过滤算法影响范围比现有的算法更好,执行时间也更有竞争力;2)k-核过滤算法对现有大多数算法都可以扩大影响范围,减少执行时间;3)k-核过滤算法在保证不降低影响范围的情况下,能大大减少CCA的执行时间。 表3 k-核过滤影响范围和执行时间百分比对比 %Tab. 3 Comparison of avg_influ_opt (AIO) and avg_time_opt (ATO) % 针对近几年研究热点社交网络影响最大化问题,提出了一种影响范围和执行时间更优的GIMS算法,并通过k-核计算剪枝影响范围小的节点,提出了一种可以扩大现有算法影响范围和减少它们执行时间的k-核过滤算法。实验表明:GIMS算法影响范围超过现有算法,执行时间也很有竞争力;k-核过滤算法能扩大现有算法的影响范围并减少它们的执行时间,对CCA尤其有效;并且,首次发现同一算法在同一数据集上预训练k选取不同种子个数时取得最佳优化效果的k是固定值。下一步的研究方向可以考虑使用其他方式来剪枝影响力小的节点,还可以考虑优化带有成本或地理位置限制的影响最大化问题[14]。 参考文献: [1]WASSERMAN S, FAUST K. Social Network Analysis: Methods and Applications [M]. New York: Cambridge University Press, 1994: 148-161. [2]DOMINGOS P, RICHARDSON M. Mining the network value of customers [C]// KDD 2001: Proceedings of the 7th ACM SIGKDD International Conference on Knowledge Discovery and Data Mining. New York: ACM, 2001: 57-66. [3]KEMPE D, KLEINBERG J, TARDOS É. Maximizing the spread of influence through a social network [C]// KDD 2003: Proceedings of the 9th ACM SIGKDD International Conference on Knowledge Discovery and Data Mining. New York: ACM, 2003: 137-146. [4]LESKOVEC J, KRAUSE A, GUESTRIN C, et al. Cost-effective outbreak detection in networks [C]// KDD 2007: Proceedings of the 13th ACM SIGKDD International Conference on Knowledge Discovery and Data Mining. New York: ACM, 2007: 420-429. [5]CHEN W, WANG Y, YANG S. Efficient influence maximization in social networks [C]// KDD 2009: Proceedings of the 15th ACM SIGKDD International Conference on Knowledge Discovery and Data Mining. New York: ACM, 2009: 199-208. [6]曹玖新,董丹,徐顺,等.一种基于k-核的社会网络影响最大化算法[J].计算机学报,2015,38(2):238-248. (CAO J X, DONG D, XU S, et al. Ak-core based algorithm for influence maximization in social networks [J]. Chinese Journal of Computers, 2015, 38(2): 238-248.) [7]WANG C, CHEN W, WANG Y. Scalable influence maximization for independent cascade model in large-scale social networks [J]. Data Mining & Knowledge Discovery, 2012, 25(3): 545-576. [8]JUNG K, HEO W, CHEN W. IRIE: scalable and robust influence maximization in social networks [C]// ICDM 2012: Proceedings of the 2012 IEEE 12th International Conference on Data Mining. Washington, DC: IEEE Computer Society, 2012: 918-923. [9]夏涛,陈云芳,张伟,等.社会网络中的影响力综述[J].计算机应用,2014,34(4):980-985. (XIA T, CHEN Y F, ZHANG W, et al. Survey of influence in social networks [J]. Journal of Computer Applications, 2014, 34(4): 980-985.) [10]李国良,楚娅萍,冯建华,等.多社交网络的影响力最大化分析[J].计算机学报,2016,39(4):643-656. (LI G L, CHU Y P, FENG J H, et al. Influence maximization on multiple social networks [J]. Chinese Journal of Computers, 2016, 39(4): 643-656.) [11]SEIDMAN S B. Network structure and minimum degree [J]. Social Networks, 1983, 5(3): 269-287. [13]BRIN S, PAGE L. The anatomy of a large-scale hypertextual Web search engine [J]. Computer Networks and ISDN Systems, 1998, 30(1/2/3/4/5/6/7): 107-117. [14]刘院英,郭景峰,魏立东,等.成本控制下的快速影响最大化算法[J].计算机应用,2017,37(2):367-372. (LIU Y Y, GUO J F, WEI L D, et al. Fast influence maximization algorithm in social network under budget control [J]. Journal of Computer Applications, 2017, 37(2): 367-372.)2.3 k-核优化现有算法
2.4 GIMS算法
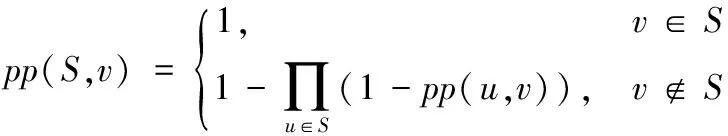
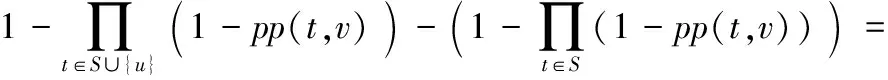
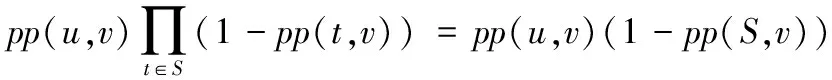
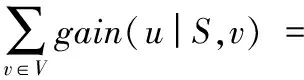
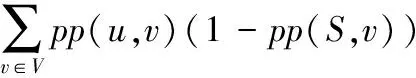
2.5 算法复杂度比较分析
3 实验与分析
3.1 数据集
3.2 实验设计
3.3 实验结果与分析
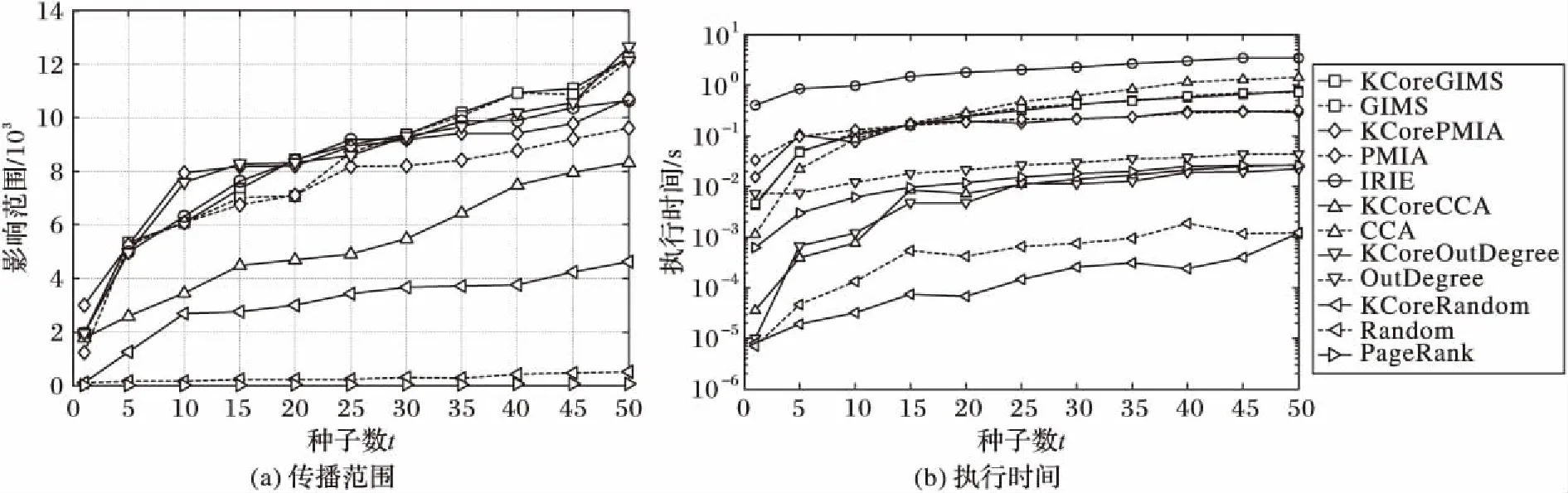
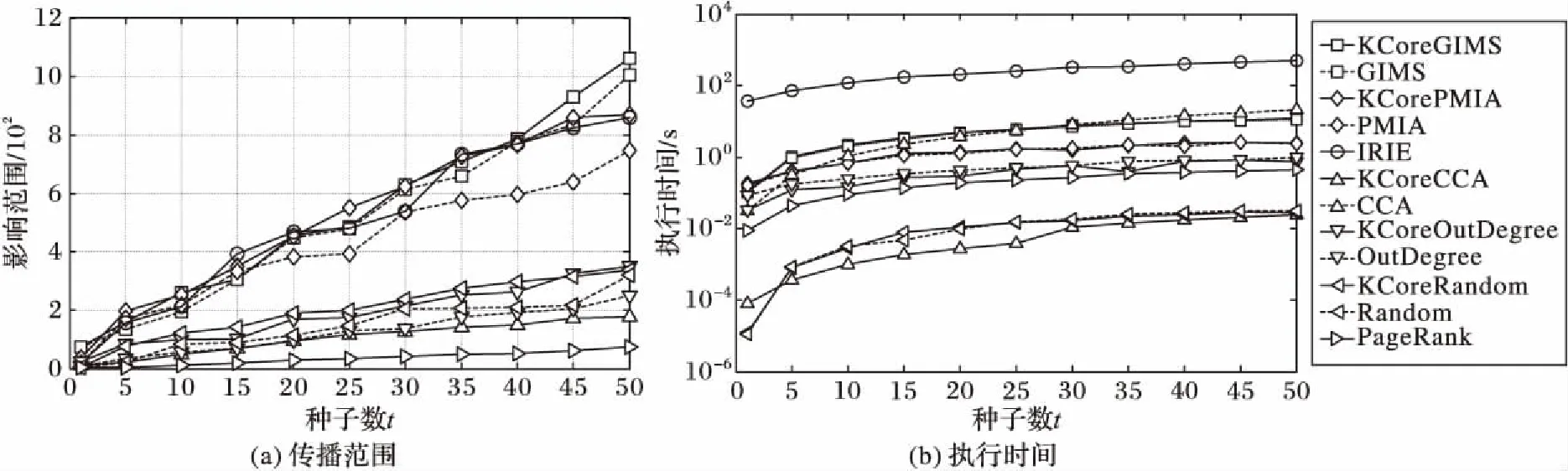
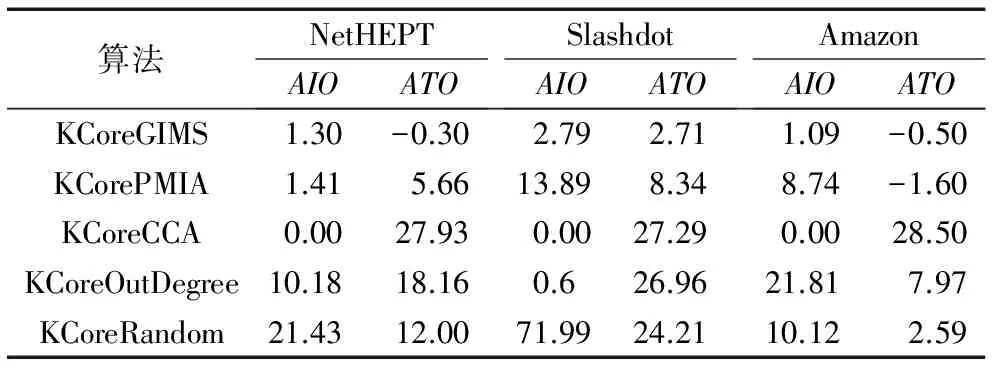
4 结语

