基于块稀疏表示的行人重识别方法
孙金玉,王洪元,张 继,张文文
(常州大学 信息科学与工程学院,江苏 常州 213164)(*通信作者电子邮箱hywang@cczu.edu.cn)
0 引言
行人重识别是计算机视觉领域的重要问题之一,其中行人重识别的任务是在非重叠摄像机拓扑结构下对同一行人的所有图像实现匹配,从而实现行人的持续跟踪。由于其在智能监控、多目标跟踪等领域具有重要的意义,近年来引起了国内外研究者的广泛关注。
行人重识别领域主要的问题在于同一个行人通常在不同时间被相互之间非重叠的摄像机所拍摄,导致拍摄到的图像会因为不同的光照条件、不同的相机视角、不同的行人姿态甚至不同的行人衣着或外观等原因,产生很大的变化。因此,行人重识别问题通常具有以下几个特点:1)在实际的监控环境中,不能有效地利用脸部的有效信息,只能利用行人的外貌特征进行识别;2)在不同的摄像头下,因尺度、光照和拍摄角度的变化,同一个行人的不同图片中,外观特征也会有一定程度的变化;3)行人姿态和摄像头角度的改变,在不同摄像头中,不同行人的外貌特征可能比同一个行人的外貌特征更相似。
基于以上问题,当前的行人重识别研究工作可以大致分为基于外貌的特征表示方法和基于距离度量学习方法两类。首先,前者利用纹理和颜色直方图等特征描述行人外貌。Gheissari等[1]提取行人外貌特征中不变的区域,在每个稳定不变的区域上提取多种颜色特征,采用三角形模型表示行人身体结构,通过模型匹配计算两个行人图像的距离;Farenzena等[2]提出基于对称驱动的累积局部特征(Symmetry-Driven Accumulation of Local Feature,SDALF)的行人重识别方法,该方法将人体按照结构划分成不同区域,分别提取加权HSV(Hue, Saturation, Value)直方图和纹理特征,再分别对不同的特征采用不同的距离函数计算相似度,最终相似度按照不同的权重将不同特征的距离加权求和得到;Cai等[3]将位置信息融入到HSV颜色直方图中,提出全局颜色背景(Global Color Context, GCC)方法。其次,基于距离度量学习的行人重识别方法则是通过对目标函数的训练,找出有最大区分度的特征分量,再进行建模实现目标重识别。Weinberger等[4]提出大间隔最近邻分类(Large Margin Nearest Neighbor, LMNN)距离测度学习算法;Zheng等[5]首次引入尺度学习算法的思想,仅采用LMNN中三元组形式的样本对,提出基于概率相对距离比较(Probabilistic Relative Distance Comparison, PRDC)的距离测度学习算法;Zheng等[6]还提出将行人重识别视作一个相对距离比较(Relative Distance Comparison, RDC)的学习问题,在该方法中,各类特征并非一视同仁对待,目的也是正样本的距离最小化及负样本的距离最大化,该方法表现出对于外观变化更大的宽容性;Zhao等[7]利用非监督学习方式来寻找目标的突出特征进行匹配;许允喜等[8]采用视觉单词树直方图和全局颜色直方图构建所跟踪目标的人体外观模型,并使用支持向量机(Support Vector Machine, SVM)增量学习进行在线训练;Xiong等[9]提出了一种新的基于内核的距离学习方法,将归一化成对约束成分分析(regularized Pairwise Constrained Component Analysis, rPCCA)方法用于行人重识别问题;Chen等[10]提出了一种相似性学习(Similarity Learning)算法,实质是基于显示内核特征图(Explicit Kernel Feature Map)计算特征相似性距离,提高算法鲁棒性;You等[11]提出top-push距离学习(Top-push Distance Learning, TDL)方法,该方法基于视频上的研究,主要思路即进一步增大行人图像的类间差异、缩小类内差异。虽然这些行人重识别方法都能取得很好的效果,但都是基于全局行人特征基础上的研究,加之行人重识别一直以来受遮挡、姿态变化、光照、视角等因素的影响,研究效果并不显著,进一步提升仍然困难重重。
近年来,稀疏表示理论在计算机视觉领域发挥了重要作用,如目标跟踪[13]以及图像复原[14]等问题。特别是人脸识别问题中,稀疏表示理论得到了广泛应用[12]。其中,稀疏表示分类(Sparse Representation-based Classifier, SRC)算法是一个比较有效的人脸识别算法[12]。基于SRC算法的主旨思想,本文假设任一张行人图像都可以用同一行人训练样本的线性组合来表示,通过寻找测试样本相对于整个训练集的稀疏表示系数来发现测试图像所属的用户身份[12]。借助于先进的高维凸优化技术(如1范数最小化[15]),稀疏表示系数可以被精确稳定地恢复出来,解的精度和鲁棒性都有理论上的保证。与现有多数方法相比,SRC方法直接利用了高维数据分布的基本特性(即“稀疏性”)进行统计推断,可以有效地应对维数灾难问题。Yang等[16]在2011年的ICCV(International Conference on Computer Vision)上提出了Fisher Discriminative Dictionary Learning(FDDL)算法来学习一个结构化字典,因此可以采用基于重构的方法来对测试样本进行分类。该算法不仅增加了字典的判别性,而且还考虑到了稀疏编码的判别性。Fisher判别准则被应用到了稀疏编码上,使得训练样本的稀疏编码具有小的类内散度和大的类间散度,这可以进一步提高学习到的字典的判别性。
然而基于稀疏表示的分类方法并没有考虑到字典的结构化。因此,Elhamifar等[17]使用稀疏表示技巧在多个子空间环境下进行分类任务。直观上来说,所有训练样本组成的字典应该具有块结构,并且来自同一个类别的训练样本组成了字典的某些块。可以将分类归结为结构化稀疏复原问题,目的是从字典中找到最少数量的字典块来表示一个测试样例。传统的基于稀疏表示分类方法旨在找到一个测试样本最稀疏的表示,但是这可能并不是最好的分类规则。
基于稀疏表示的分类方法在行人重识别问题上未曾受到广泛关注,虽然有些方法采取稀疏表示[18-19],但并未利用到行人特征字典固有的块结构[17]。
针对上述问题,本文提出一种新的方法用于行人重识别问题。将分类归结为块结构化稀疏复原问题,与传统的基于稀疏表示的分类方法旨在找到一个测试样本最稀疏的表示不同的是,本文方法目的是从字典中找到最少数量的字典块来表示一个测试样例。之后利用交替方向框架求解相关块稀疏极小化问题,并且在公开的数据集PRID 2011[21]、iLIDS-VID[22]和VIPeR[23]上进行实验,证实了该方法与同类方法比较时(特别是那些涉及复杂背景以及有遮挡的场景)的优越性与鲁棒性。
1 块稀疏模型构建
1.1 特征提取
在行人图像特征描述中,颜色特征是最基本、最重要的图像特征,而纹理特征描述图像的结构特性,因此可以利用纹理特征对颜色特征进行补充。本文采用颜色特征与纹理特征结合的特征表示方法。首先将图像归一化为128像素×48像素大小,并且分块为32像素×48像素大小,且每一小块在水平和竖直方向上均有50%的重叠部分,因此就有7个分块用于提取HS(Hue, Saturation)颜色直方图、Lab特征和Gabor特征。其中HSV特征只提取色调(即H分量)、饱和度(即S分量)特征是因为在行人重识别研究中通常需要排除光照带来的影响。Lab特征为颜色空间特征,提取的是直方图特征,该特征是一种统计特征。在Lab颜色空间中,一种颜色由L(亮度)、a颜色、b颜色三种参数表征。由于行人重识别受亮度影响比较大,因此该特征仅提取a通道和b通道的颜色特征,并将这些待提取的特征全部分为16维直方图统计特征。而Gabor特征是一种纹理特征,根据不同波长、方向、空间纵横比、带宽等分别取16组不同的Gabor滤波器。由图像划分方法可知,对于每一张行人图像,其在水平方向有7个分块,由上面特征提取的内容可知,每个块中通道包括16个Gabor、2个HS和2个Lab,即有20(16+2+2=20)个特征通道,每个通道又被表示为16维直方图向量。所以每幅图像在特征空间中被表示为2 240维度的全局图像特征向量。
针对行人的高维特征在识别过程中易造成维数灾难问题,可以采用典型相关分析(Canonical Correlation Analysis, CCA)[20]对行人的高维特征进行转换。它能对给定的两组变量寻找一组线性映射,将多维数据投影到一个子空间中,使投影后的两组数据间的相关性达到最大,能在一定程度上有效避免原本高维特征在运算中所引起的维数灾难。CCA是一种简单的用于求投影矩阵的方法,同时也是一种统计两组随机变量之间关系的数学方法,目前,CCA已被广泛应用于行人重识别领域。因此采用CCA[20]对特征进行投影,使经过投影空间后的行人特征更具有匹配重识别的能力,能大幅提高重识别率。
1.2 基于块稀疏表示的行人重识别
1.2.1问题描述
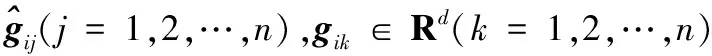
设带有标记i行人的n幅图像提取的特征数据形成字典Gi=[gi1gi2…gin]∈Rd×n。现给定一张待识别行人图像p,假设其属于第i个行人,则理论上只需用第i个行人的数据集图像特征向量就能线性表示p[12],即:
p≈xi1gi1+xi2gi2+…+xingin
(1)
其中xij∈R(j=1,2,…,n)表示带有标记i的第j个样本的权重系数。该等式可以简洁地记为:
p≈Gixi
(2)
然后构建所有数据集特征字典D∈Rd×N为:
D=[G1G2…GZ]
(3)
其中N=Z×n为所有在数据集中出现的图像总数。显然,该数据字典是由Z个独立块向量串联而成,因此它具有块结构[17]。这是多目标配准行人重识别问题的一大特点,本文就是利用该特点设计一个基于块稀疏的行人重识别方法。
令x=[x1Tx2T…xZT]T因此,可以建立模型:
pij≈G1x1+G2x2+…+GKxZ
(4)
其中xi=[xi1xi2…xin]T∈Rn表示与带有标记i的行人相对应的系数块。由于p与行人i的字典Gi近似呈线性关系,且注意到向量块xi要比向量块xz(z=1,2,…,Z,z≠i)对最优解向量x的贡献大,也就是模型的系数向量主要由系数块xi所决定。
同时模型为:
p≈Dx
(5)
其中x∈RN是稀疏的。也就是当数据集字典D中的行人数量较多时,x中只会有少量的非零项,大部分的系数为0。本文所要寻找的即非零项集中在特定行人特征字典块上的解向量,因此采用稀疏的目的就是求解稀疏系数矩阵X。
如文献[12]中所述,本文所提的问题如下述L1/L2优化问题:
(6)
s.t.p=Dx
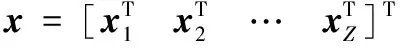
1.2.2遮挡造成数据损坏
从监控摄像机捕获的行人图像通常被其他人或者物体遮挡,所提取的行人特征数据因此被损坏,例如图1所示的样例图像。由于行人遮挡、相机分辨率低等问题,会极大降低行人重识别的精度,并且该情况下的行人图像处理会产生较大误差,因此需要对遮挡物进行误差建模处理,平衡由此产生的误差。与其他相关多目行人重识别技术不同的是,本文的制定方法明确地建模遮挡物,即引入一个误差项e∈Rd到式(5)里,则线性近似模型为:
p=Dx+e
(7)

图1 在iLIDS-VID数据集里被遮挡的行人Fig. 1 Occluded people in iLIDS-VID dataset
式(7)的最小化问题可以表述如下:
(8)
s.t.p=Dx+e
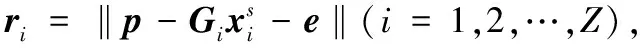
1.2.3使用交替方向的块稀疏恢复
给定数据p和D,使用交替方向框架来计算式(7)的解。首先,引入松弛变量s∈RN,式(8)的问题可重新建模为:
(9)
s.t.s=x
p=Dx+e
现引入Lagrange乘数α∈RN,β∈Rd将式(9)的约束最小化问题转换为下述无约束的最小化问题:
(η1/2)‖s-x‖2+(η2/2)‖Dx+e-p‖2
(10)
在损失函数中增加两个二次惩罚项(η1/2)‖s-x‖2和(η2/2)‖Dx+e-p‖2来最小化目标。观察到最小化该损失函数涉及到三个变量s,x和e,因此本文采用交替方向迭代框架,最小化单变量损失函数,即每次迭代仅与一个变量相关,其他两个变量保持固定。
首先,固定s和e并最小化变量为x的损失函数:
(η1/2)‖s-x‖2+(η2/2)‖Dx+e-p‖2
(11)
该x的子问题是一个简单的二次优化目标问题,其闭合解为:
x*=(η1I+η2DTD)-1(η2DT(p-e)+η1s+βTD-α)
(12)
其次,固定s和x,并最小化变量为e的损失函数:
(13)
x*是上述x子问题的最优解。同样e的子问题也有一个闭式解,即:
e*=shrink(β/η2-Dx*-p,1/η2)
(14)
shrink(t,α)=sgn(t)⊗max{|t|-α,0},其中⊗表示矩阵之间的点乘。
最后,通过固定x和e并最小化变量为s的损失函数,得到:
(15)
该s子问题也有一个闭式解,并且该解对每个分块的系数i=1,2,…,Z是由块收缩[13]运算得到:
(16)
最后,更新拉格朗日乘数为:
α=α-η1(s*-x*)
(17)
β=β-η2(Dx*+e*-p)
(18)
对于以上变量s、e和x的具体求解,则通过初始化变量s=0,e=0,α=0,β=0进行迭代,实现如算法1所示。
1.2.4重识别
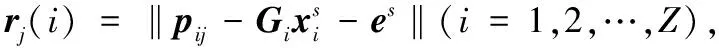
算法1迭代稀疏重识别算法。
Input:p∈Rd,D∈Rd×N;
Output: index of the correct peoplec。
Initialize:s=0,e=0,α=0,β=0,t←1,2,…。
1)
whileet<10-3do
2)
computextusing equation (12)
3)
computeetusing equation (14)
4)
computestusing equation (16)
5)
updateα,βusing equation (17), (18)
6)
end while
7)
xs=xt;es=et;
8)
computestusing equation (16)
9)
letR=0
10)
forj=1:n
11)
computepin equation (9) withxs,es
12)
compute residuals vector
13)
14)
R=R+rj
15)
end for
16)
c=index of the minimum value inR
2 实验和结果分析
实验在公开数据集PRID 2011[21]iLIDS-VID[22]和VIPeR[23]上进行,验证了所提方法在多目标配准行人重识别下的效果。
iLIDS-VID:此数据集是从机场到达大厅的两个非重叠相机视角中提取图像创建而成。其随机为300个行人采样了600个视频,每个行人均有来自于两个摄像机视角的一组视频。 每个视频有23~192帧,平均73帧。在此数据集中所有图像大小为128×64,图像特点是受到极度光照、视角的变化、遮挡和杂乱的背景影响较严重。
PRID 2011:此数据集是由两个相邻摄像机捕获室外场景所创建,主要涉及到视角、遮挡以及背景变化。其中摄像头A有385个行人,摄像头B有749个行人,其中有200个行人同时在摄像头A和摄像头B中;所有图像大小归一化为128×48大小。本文主要选择200个同时在两个摄像头下出现的行人图像作实验。
VIPeR:此数据集是由在校园环境中录制的视频制作而成。其图像包括两个摄像头下的632个行人的1 264张图像,且全部归一化为128×48大小。每个摄像头下的每个行人有且仅有一张图像;不同摄像头下的同一行人的图像受视角和光照影响,使得外貌存在明显差异,其中视角不同是造成外貌差异的主要原因。
2.1 实验过程
对每个数据集进行以下操作:1)随机选择行人图像将之划分为大小相等的训练集和测试集。由于本文所选择的数据集中每个行人有多张图像,所以每一个行人在数据集视角和查询集视角下都随机选择各5张图像提取行人特征。2)将训练集用于学习投影矩阵并将测试集行人特征投影到该投影空间。3)同一个相机视角下(camA)所有行人图像特征形成数据集字典D,而另一相机视角下(camB)的行人图像则作为查询集。4)对查询集里的每个行人图像一一计算其与数据集里每张图像的残差,按照残差大小对数据集进行排序,并记录正确的目标所在的位置。为了得到稳定可靠的实验结果并减少随机因素所带来的不可控影响,对上述过程重复10次,取其平均值作为最终结果。
本文关于行人重识别性能的评估主要采用累积匹配特征(Cumulative Matching Characteristic, CMC)曲线作为指标。CMC曲线在行人重识别算法的性能评测上应用广泛[4,6-7,11], 曲线上的数值反映出在前i个搜索中匹配到正确目标的概率。Ranki表示第i个Rank值。
2.2 实验结果分析
将本文方法与近年提出的几种方法进行比较,包括LMNN[4]、RDC[6]、TDL[11]和SDALF[2]。首先,评估数据集上的CMC曲线如图2所示。从图2可以看到,本文方法的Rank1性能在三个数据集上分别达到40.4%、38.11%和23.68%;Rank5上的性能分别达到64.63%、60.13%和51.5%;Rank10的性能达到75.34%、70.31%和65.32%;Rank20的性能达到了84.08%,79.73%和77%,均处于领先水平。与其他同类方法相比,在数据集PRID 2011、iLIDS-VID和VIPeR上,本文方法在Rank1、5、10和20排名上得到了较好的性能。其中在Rank1性能上,本文方法匹配率远大于LMNN算法;总体性能均优于经典的基于特征表示与度量学习的对比算法。
本文对行人特征的提取主要是针对多种特征进行融合以及对图像进行分块处理,因此提取不同种类的特征对实验结果的影响较为显著。实验中所有对比方法均使用相同的、由本文方法所提取的特征,这些特征与各方法原文献中是不同的,同样具有说服力。如图3所示,在PRID 2011数据集上,提取Lab、HS、Gabor特征以及对行人分块后的效果要明显好于其他几种特征提取方式;同样,在数据集iLIDS-VID和VIPeR上,本文所用的特征提取方式效果也明显优于其他特征提取方式。
本文对行人特征进行转换时主要是进行空间投影,因此对所提方法在投影空间与基础空间的比较必不可少。此时在两个空间中,对行人特征的提取均需保持一致,唯一不同之处在于特征投影空间是否转换。如图4所示,应用本文方法的投影空间,在PRID 2011、iLIDS-VID和VIPeR数据集上,Rank1的性能比基础空间分别提升了24.74个百分点、21.97个百分点和10.23个百分点。从图中也注意到当所提方法应用在投影空间与应用在基础特征空间中相比时,在各等级排名中,投影空间中的结果始终比基础空间的好。该实验也验证了本文提出的关于在投影空间里制定一个线性近似模型而不是基础特征空间的原假设。
针对本文式(8)的模型,误差项e主要用于避免数据损坏或者应对行人受遮挡问题,更好地建模遮挡物。如果不引入误差项,则同样条件下的行人重识别效果会受很大影响。表1为引入误差项e与未引入误差项e的效果比较,说明对遮挡物建模可以更好地对行人进行匹配。
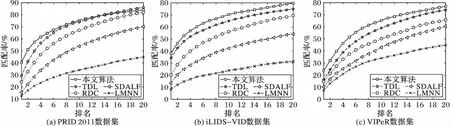
图2 不同方法的CMC曲线Fig. 2 CMC curves for different methods
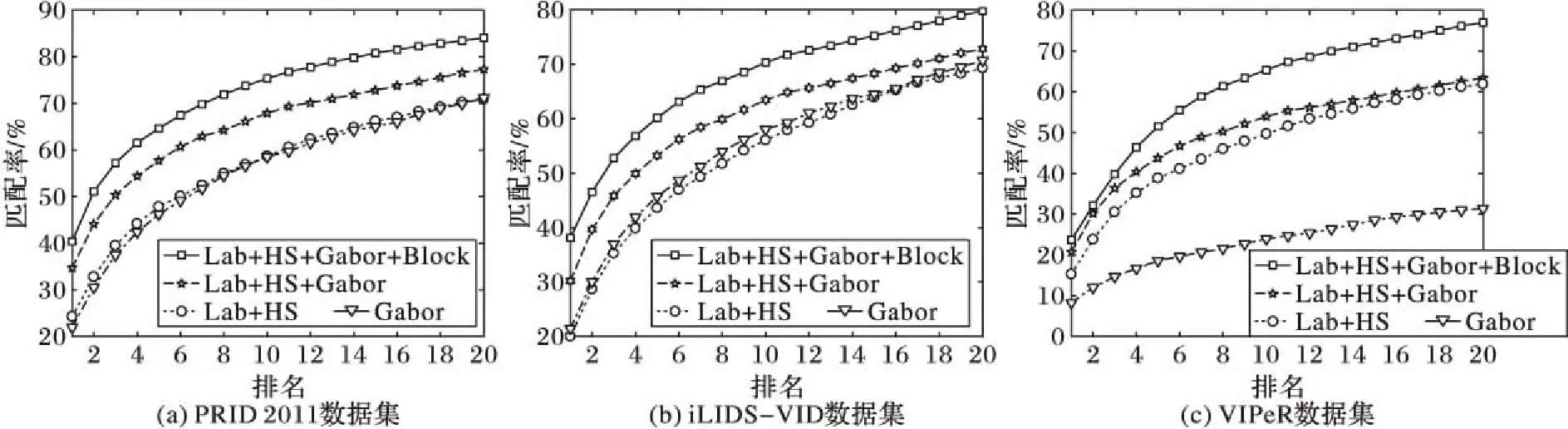
图3 不同种类特征对行人重识别结果影响Fig. 3 Impact on different kinds of features on re-identification
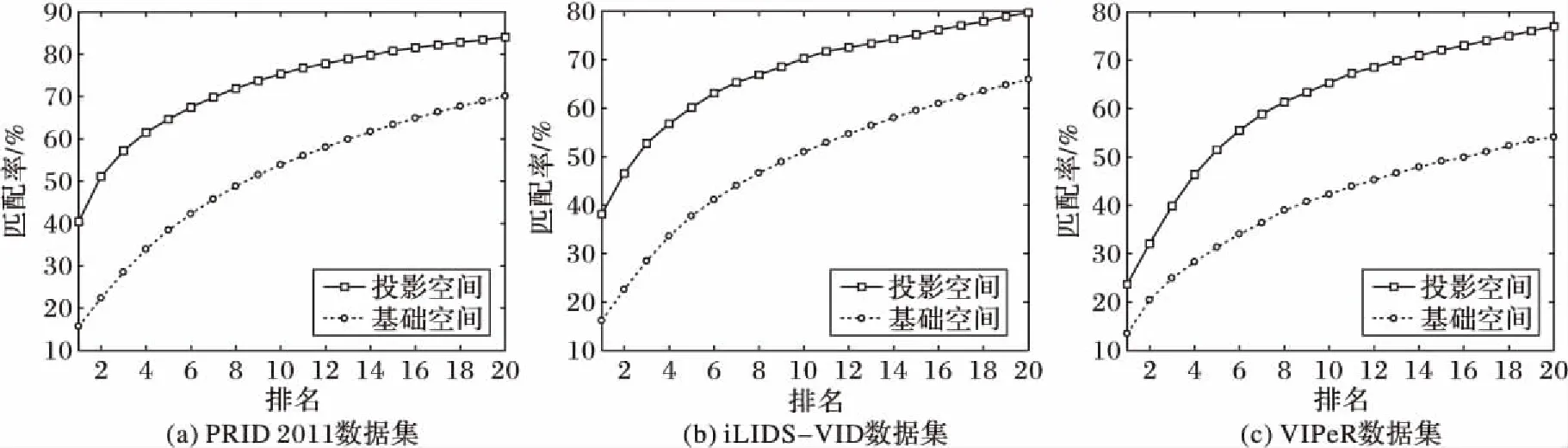
图4 投影空间与基础空间比较Fig. 4 Comparison of projected space and original space
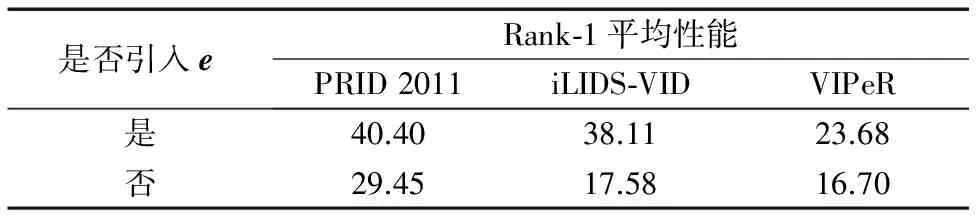
表1 误差项e的引入对Rank-1平均性能的影响 %Tab. 1 Impact of the error term e on average Rank-1 performance %
3 结语
本文主要提出一种行人重识别的方法:首先利用CCA方法对高维的行人特征进行转换,有效缓解高维特征运算带来的维数灾难问题;接着将查询集图像的特征向量投影到学习到的投影空间,使投影后查询集行人特征向量与相应的数据集特征向量近似呈一个线性关系;最后构建一个关于数据集特征向量的字典D,将重识别作为一个块的稀疏极小化问题并利用其内在结构,采用交替方向框架求解该极小化问题。对于行人身份判别问题,采用残差项进行处理,最终的残差项中最小值所对应的指标将作为重识别行人的识别标记。最后在公开的标准行人数据集PRID 2011、iLIDS-VID和VIPeR上评估所提方法,验证了本文方法的优越性。但本文方法仍具有一定的局限性,正如在2.2节图2(a)所示,由于TDL将行人重识别问题看作度量学习问题来解决,结合top-push约束模型,在匹配精度上更精准,导致本文方法在Rank-10之后的排名与TDL方法相仿,但这并不影响本文方法的整体性能。接下来的研究将与监督学习相结合,尽可能利用已知标签信息的行人特征,提高行人重识别的匹配精度,为进一步研究提供了提升空间以达到更好的突破。
参考文献:
[1]GHEISSARI N, SEBASETIAN T B, HARTLEY R. Person reidentification using spatiotemporal appearance [C]// CVPR ’06: Proceedings of the 2006 IEEE Computer Society Conference on Computer Vision and Pattern Recognition. Washington, DC: IEEE Computer Society, 2006, 2: 1528-1535.
[2]FARENZENA M, BAZZANI L, PERINA A. Person re-identification by symmetry-driven accumulation of local features [C]// CVPR ’10: Proceedings of the 2010 IEEE Computer Society Conference on Computer Vision and Pattern Recognition. Washington, DC: IEEE Computer Society, 2010: 2360-2367.
[4]WEINBERGER K Q, SAUL L K. Distance metric learning for large margin nearest neighbor classification [J]. The Journal of Machine Learning Research, 2006, 10: 207-244.
[5]ZHENG W-S, GONG S, XIANG T. Person re-identification by probabilistic relative distance comparison [C]// CVPR ’11: Proceedings of the 2011 IEEE Computer Society Conference on Computer Vision and Pattern Recognition. Washington, DC: IEEE Computer Society, 2011: 649-656.
[6]ZHENG W-S, GONG S, XIANG T. Re-identification by relative distance comparison [J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2013, 35(3): 653-668.
[7]ZHAO R, OUYANG W, WANG X. Unsupervised salience learning for person re-identification [C]// CVPR ’13: Proceedings of the 2013 IEEE Computer Society Conference on Computer Vision and Pattern Recognition. Washington, DC: IEEE Computer Society, 2013: 3586-3593.
[8]许允喜,蒋云良,陈方.基于支持向量机增量学习和LBPoost的人体目标再识别算法[J].光子学报,2011,40(5):758-763. (XU Y X, JIANG Y L, CHEN F. Person re-identification algorithm based on support vector machine incremental learning and linear programming boosting [J]. Acta Photonica Sinica, 2011, 40(5): 758-763.)
[9]XIONG F, GOU M, CAMPS O, et al. Person re-identification using kernel-based metric learning methods [C]// ECCV 2014: Proceedings of the 2014 European Conference on Computer Vision, LNCS 8695. Cham: Springer, 2014: 1-16.
[10]CHEN D, YUAN Z, HUA G, et al. Similarity learning on an explicit polynomial kernel feature map for person re-identification [C]// CVPR ’15: Proceedings of the 2015 IEEE Computer Society Conference on Computer Vision and Pattern Recognition. Washington, DC: IEEE Computer Society, 2015: 1565-1573.
[11]YOU J, WU A, LI X, et al. Top-push video-based person re-identification [C]// CVPR ’16: Proceedings of the 2016 IEEE Computer Society Conference on Computer Vision and Pattern Recognition. Washington, DC: IEEE Computer Society, 2016: 1345-1353.
[12]WRIGHT J, YANG A Y, GANESH A, et al. Robust face recognition via sparse representation [J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2008, 31(2): 210-227.
[13]ZHANG T, GHANEM B, LIU S, et al. Robust visual tracking via structured multi-task sparse learning [J]. International Journal of Computer Vision, 2013, 101(2): 367-383.
[14]MAIRAL J, SAPIRO G, ELAD M. Learning multiscale sparse representations for image and video restoration (PREPRINT)[J]. SIAM Journal on Multiscale Modeling and Simulation, 2008, 7(1): 214-241.
[15]YANG A Y, SASTRY S S, GANESH A, et al. Fast1-minimization algorithms and an application in robust face recognition: a review [C]// ICCP 2010: Proceedings of the 2010 17th IEEE International Conference on Image Processing. Piscataway, NJ: IEEE, 2010: 1849-1852.
[16]YANG M, ZHANG L, FENG X, et al. Fisher discrimination dictionary learning for sparse representation [C]// ICCV ’11: Proceedings of the 2011 IEEE International Conference on Computer Vision. Washington, DC: IEEE Computer Society, 2011: 543-550.
[17]ELHAMIFAR E, VIDAL R. Robust classification using structured sparse representation [C]// CVPR ’11: Proceedings of the 2011 IEEE Computer Society Conference on Computer Vision and Pattern Recognition. Washington, DC: IEEE Computer Society, 2011: 1873-1879.
[18]HARANDI M T, SANDERSON C, HARTLEY R, et al. Sparse coding and dictionary learning for symmetric positive definite matrices: a kernel approach [C]// ECCV 2012: Proceedings of the 2012 European Conference on Computer Vision, LNCS 7573. Berlin: Springer, 2012: 216-229.
[19]KHEDHER M I, YACOUBI M A E, DORIZZI B. Multi-shot SURF-based person re-identification via sparse representation [C]// AVSS 2013: Proceedings of the 2013 10th IEEE International Conference on Advanced Video and Signal Based Surveillance. Washington, DC: IEEE Computer Society, 2013: 159-164.
[20]AN L, YANG S, BHANU B. Person re-identification by robust canonical correlation analysis [J]. IEEE Signal Processing Letters, 2015, 22(8): 1103-1107.
[21]HIRZER M, BELEZNAI C, ROTH P M, et al. Person re-identification by descriptive and discriminative classification [C]// SCIA 2011: Proceedings of the 2011 Scandinavian Conference on Image Analysis, LNCS 6688. Berlin: Springer, 2011: 91-102.
[22]WANG T, GONG S, ZHU X, et al. Person re-identification by video ranking [C]// ECCV 2014: Proceedings of the 2014 European Conference on Computer Vision, LNCS 8692. Cham: Springer, 2014: 688-703.
[23]GRAY D, BRENNAN S, TAO H. Evaluating appearance models for recognition, reacquisition, and tracking [C]// PETS 2007: Proceedings of the 10th IEEE International Workshop on Performance Evaluation for Tracking and Surveillance. Piscataway, NJ: IEEE, 2007, 3: 41-47.

