基于Lévy飞行的差分乌鸦算法求解折扣{0-1}背包问题
刘雪静,贺毅朝,路凤佳,吴聪聪,才秀凤
(河北地质大学 信息工程学院,石家庄 050031)(*通信作者电子邮箱lxjpass@163.com)
0 引言
0-1背包问题(0-1 Knapsack Problem, 0-1 KP)[1]是计算机科学中典型的优化难题,已应用于很多领域,如资源分配、项目组合、整数规划等。多维背包问题(MultiDimensional Knapsack Problem, MDKP)[2]、二次背包问题(Quadratic Knapsack Problem, QKP)[3]、多重二次背包问题(Quadratic Multiple Knapsack Problem, QMKP)[4]、折扣0-1背包问题(Discount {0-1} Knapsack Problem, D{0-1}KP)[5]都是0-1 KP的扩展形式。其中,D{0-1}KP源于商业领域的打折思想,是新型的0-1KP,目前D{0-1}KP的研究成果相对较少。
2007年,Guldan[5]首先提出了D{0-1}KP,并利用动态规划法求解;Rong等[6]将D{0-1}KP的核(Core)问题与动态规划法相结合求解D{0-1}KP;贺毅朝等[7]利用精英遗传算法求解D{0-1}KP,首先利用演化算法求解D{0-1}KP,得到近似比接近1的近似解;He等[8]提出利用精确和近似算法求解D{0-1}KP,提出了求解该问题的精确算法、近似算法和利用二进制粒子群算法求解的有效方法;刘雪静等[9]提出利用细菌觅食算法求解D{0-1}KP,并给出了两种D{0-1}KP数学模型的求解算法;吴聪聪等[10]提出利用变异蝙蝠算法求解D{0-1}KP,能得到较好的最优解;Zhu等[11]利用差分演化求解D{0-1}KP,给出了求解该问题的三个高效离散演化算法。目前,D{0-1}KP是{0-1}KP的一个热点问题,如何利用启发式算法快速求解D{0-1}KP是一个非常值得研究的问题。
针对D{0-1}KP的第二数学模型的编码和优化问题,本文利用改进的乌鸦算法(Crow Search Algorithm,CSA)[12]进行求解。首先介绍D{0-1}KP的第二数学模型,并利用混合编码方式解决其整数编码问题;其次采用新的贪心修复与优化算法(New greedy Repair and Optimization Algorithm, NROA)处理潜在解;然后,对CSA进行改进,分别引入差分策略和Lévy飞行策略,进一步提高算法的收敛速度和求解精度。实验表明:改进的乌鸦算法非常适于求解D{0-1}KP,其效果优于文献[7]中的Second Genetic Algorithm with Elitist reservation strategy(SecEGA)算法和文献[9]中的Second Bacterial Foraging Optimization(SecBFO)算法。
1 D{0-1}KP问题
定义1[5]给定n个项集,且每一个项集中均含3项,项集i(0≤i≤n-1)中的3项为3i、3i+1和3i+2;项3i的价值系数为p3i,重量系数为w3i;项3i+1的价值系数为p3i+1,重量系数为w3i+1;项3i+2的价值系数为p3i+2,且p3i+2为p3i和p3i+1的和,重量系数为w3i+2,且w3i+2分别大于w3i和w3i+1,并小于w3i和w3i+1的和;每一项集中至多有一项可以被装入背包中。D{0-1}KP为如何选择装入背包的项,使得装入背包的所有项的价值系数之和达到最大且其重量系数之和不超过背包载重C。

文献[5]给出了D{0-1}KP的第一数学模型,本文研究如何基于D{0-1}KP的第二数学模型[7]进行有效求解。首先给出该模型的描述如下:
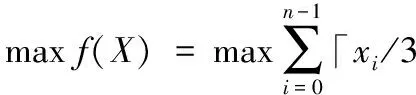
(1)

(2)
xi∈{0,1,2,3};i=0,1,…,n-1
(3)
其中:「x⎤表示向上取整;xi(0≤i≤n-1)的值表示项集i装入背包的项,xi=0表示没有项装入背包,xi=1表示项3i被装入背包,xi=2表示项3i+1被装入背包,xi=3表示项3i+2被装入背包。任意向量X=[x0,x1,…,xn-1]∈{0,1,2,3}n仅表示D{0-1}KP的一个潜在解,满足约束条件(2)和(3)的X才是D{0-1}KP的一个可行解。
2 乌鸦算法
乌鸦算法[12]是模拟乌鸦搜索食物的行为的新型演化算法。自然界中的乌鸦有如下行为:乌鸦以群居的形式生活,乌鸦能记住它们藏匿食物的最佳位置,乌鸦能跟踪其他乌鸦以窃取对方的食物,乌鸦能以一定的概率保护自己的食物以防被窃取。
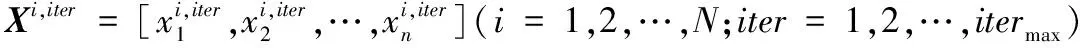
Xi,iter+1=
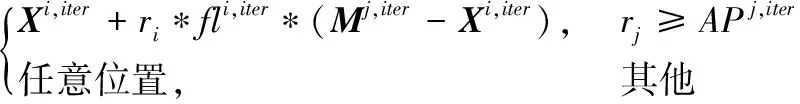
(4)
其中:ri、rj是 [0,1]内服从均匀分布的随机数。
当乌鸦i的位置发生改变,则以式(5)的方式更新记忆值。
(5)
CSA的算法描述如下:
算法1CSA。
输入参数N,n,itermax,AP,fl;
输出最优解Mbest及其目标函数值f(Mbest)。
1)
InitializeNcrows in thendimension search space randomly
2)
Calculate the fitness(Xi) (i=1,2,…,N)
3)
InitializeMof each crow
4)
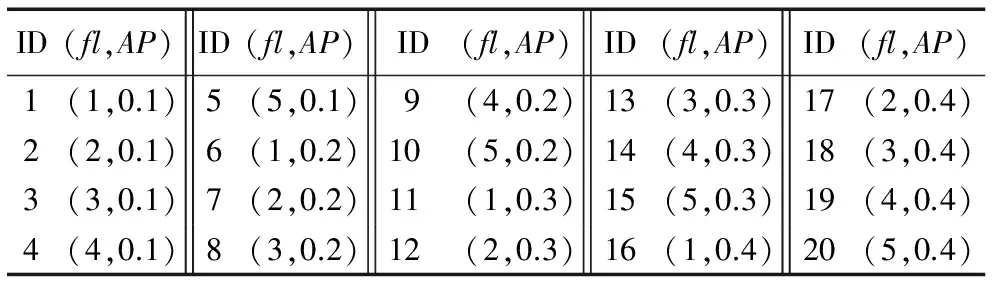
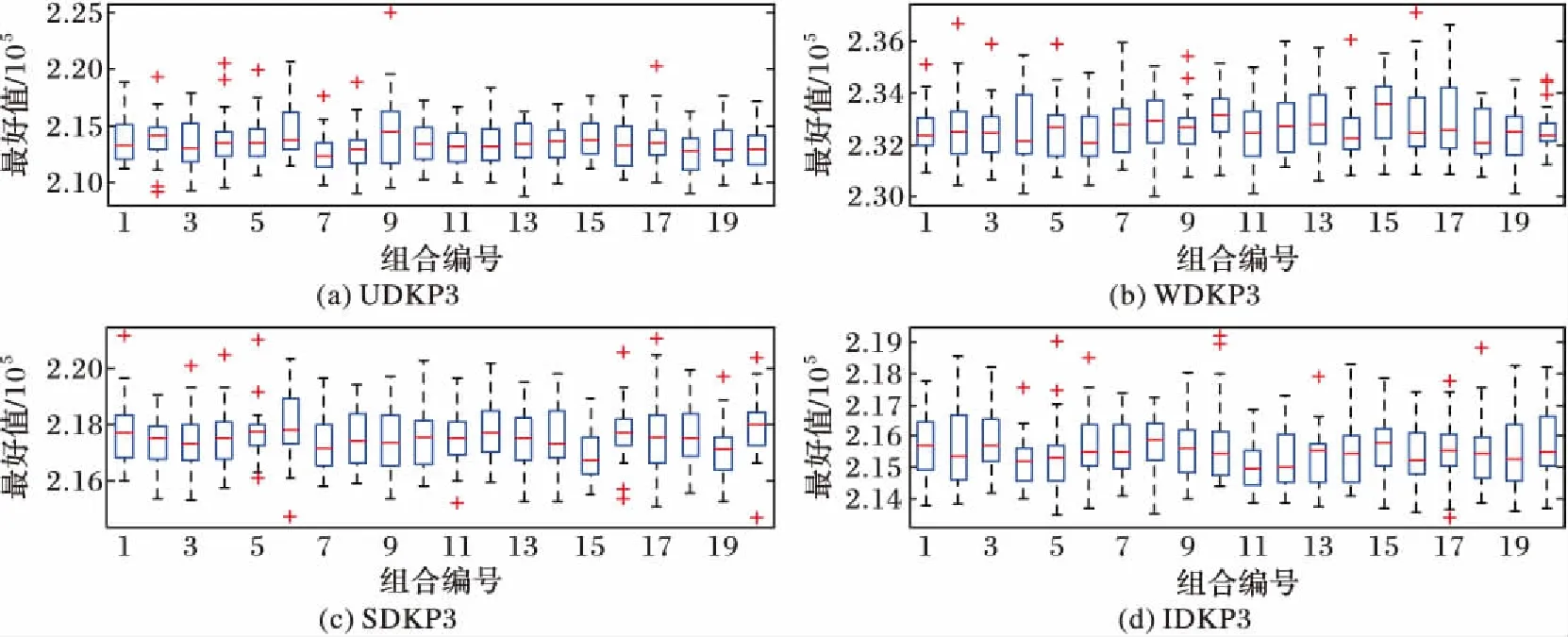
whileiter 5) fori←1 toN 6) Choose a crow randomly(for examplej) 7) ifrj≥APj,iter 8) Xi,iter+1←Xi,iter+ri*fli,iter*(Mj,iter-Xi,iter) 9) else 10) Xi,iter+1←a random position 11) endif 12) Evaluate the new position of the crows 13) UpdateMi 14) endfor 15) endwhile 16) return(Mbest,f(Mbest)) 当达到最大迭代次数itermax时,所有乌鸦的Mi(i=1,2,…,N)中的最好位置即为最优化问题的解。步骤1)~3)的时间复杂度为O(Nn),步骤4)~15)的时间复杂度为itermax*O(Nn),由于itermax、N是关于n的线性函数,故CSA的时间复杂度为O(n3)。 在CSA中,仅有AP和fl两个可调节参数,是一个参数较少的简单的算法,在参数设置方面具有一定的优势。在CSA中,集约化和多元化主要受到参数AP的控制。降低AP的值,CSA倾向于局部搜索,因此,较小的AP值增强了集约化。相反,增加AP的值,CSA趋向全局搜索,故较大的AP值增强了多元化。 本章主要介绍求解D{0-1}KP时CSA用到的几种策略及其对应的算法。 基本CSA用来求解连续空间的优化问题,而D{0-1}KP是离散域的问题,本文利用混合编码方式[13]实现CSA对离散空间问题的求解。所用的编码转换方法如式(6)所示: (6) 其中:k∈{1,2,3};xi∈(-4,4),yi∈{0,1,2,3},i=0,1,…,n-1。 由此,乌鸦个体用混合编码(X,Y)表示,其中,X为n维实型向量,Y为n维整型向量,由此以(-4,4)n为辅助搜索空间,以{0,1,2,3}n为解空间,解决了D{0-1}KP的编码问题。 由于任意整数向量X=[x0,x1,…,xn-1]∈{0,1,2,3}n仅仅是D{0-1}KP的潜在解,可能是非正常编码个体,因此利用文献[7]中提出的处理非正常编码的算法NROA对X进行修复并优化。假定原始编码个体X=[x0,x1,…,xn-1]∈{0,1,2,3}n,Y=[y0,y1,…,yn-1]∈{0,1,2,3}n为修正后个体,数组H[0,1,…,3n-1]中存放按价值系数密度pj/wj(0≤j≤3n-1)降序排序后各项所对应的下标,价值系数集P、重量系数集W和背包容量C定义同前,则NROA的伪代码描述如下。 算法2NROA。 输入个体X=[x0,x1,…,xn-1]和数组H[0,1,…,3n-1]; 输出修复与优化后的个体Y=[y0,y1,…,yn-1]及其适应度f(Y)。 1) w=0,v=0 2) fori=0 to 3n-1 3) k=⎣H[i]/3」,m=H[i]mod 3 4) if((xk==m+1)&&(w+wH[i]≤C)) 5) w=w+wH[i],yk=m+1,v=v+pH[i] 6) endif 7) if((xk==m+1)&&(w+wH[i]>C)) 8) yk=0 9) endif 10) endfor 11) fori=0 to 3n-1 12) k=⎣H[i]/3」,m=H[i]mod 3 13) if((xk==0)&&(w+wH[i]<=C)) 14) w=w+wH[i],yk=m+1,v=v+pH[i] 15) endif 16) endfor 17) return(Y,f(Y)) 算法2中步骤2)~ 10)将非正常编码个体X修复为正常编码个体并存于Y中,其时间复杂度为O(n);步骤11)~16)对Y作进一步的优化处理,其时间复杂度为O(n),因此算法NROA的时间复杂度为O(n)。 为了避免CSA中的乌鸦个体过早地陷入局部极值,在算法中引入Lévy飞行[14-15]。Lévy 飞行是服从Lévy 分布的随机搜索路径,是一种短距离的搜索与偶尔较长距离的行走相间的行走方式。经Reynolds[14]研究发现,对于个体相互独立的种群,当解在解空间中稀疏且随机分布时,Lévy 飞行是一种非常理想的搜索策略,能增加种群多样性、扩大搜索范围,有助于跳出局部最优。 在CSA中,执行完跟踪操作的乌鸦个体按照一定概率(本文为0.5)进行Lévy飞行。Lévy 飞行的位置更新公式如下: (7) 由此,基于Lévy 飞行的CSA(Crow Search Algorithm based on Lévy flight, LCSA)求解D{0-1}KP的算法如下。 算法3LCSA。 输入参数N,n,itermax,AP,fl,a; 输出最优解Mbest及其目标函数值f(Mbest)。 1) InitializeNcrows in thendimension search space randomly 2) Calculate the fitness of crows 3) InitializeMi(i=1,2,…,N) 4) H[0,1,…,3n-1]←QuickSort(pi/wi) 5) whileiter 6) fori=1 toN 7) Select cowjrandomly and track according to formula (4) 8) ifrand()>0.5 9) Crowido Lévy flight 10) endif 11) RepairXiusing NROA and calculatefitness(Xi) 12) UpdateMi 13) endfor 14) endwhile 15) return(Mbest,f(Mbest)) 在算法3中,利用QuickSort(pi/wi)按价值系数密度对各项进行快排序,并把下标放入数组H中。在LCSA中,Lévy飞行的时间复杂度为O(n),算法QuickSort的时间复杂度为O(nlogn),生成初始种群的时间复杂度为O(nN),NROA的时间复杂度为O(n)。由于N和itermax是关于n的线性函数,因此算法3的时间复杂度为O(nlogn)+O(nN)+O(n)+itermax*(N*(O(n)+O(n)+O(n))=O(n3)。 在CSA中,乌鸦i随机选择一只乌鸦j进行跟踪,以式(4)的方式向乌鸦j的Mj,iter位置移动。但是乌鸦j的Mj,iter值不一定好,可能导致算法收敛较慢,因此,在算法中引入差分策略改进乌鸦的跟踪方式。差分演化(Differential Evolution, DE)算法中变异算子的一般形式为DE/x/y/z[16],其中:x代表被扰动的基向量;y代表使用的差分向量的个数;z代表交叉的类型,Bin代表二项式交叉,Exp代表指数交叉。由于在CSA的跟踪过程中仅涉及乌鸦i和乌鸦j两个个体,故本文仅对DE/best/1/Bin和DE/best/1/Exp这两种变异算子形式进行实验来决定采用哪种形式的跟踪方式,实验结果见4.2节。基于差分的CSA(Crow Search Algorithm based on Differential Evolution, DECSA)描述如下。 算法4DECSA。 输入参数N,n,itermax,AP,fl,Cr; 输出最优解Mbest及其目标函数值f(Mbest)。 1) Initialize crowsXi(i=1,2,…,N) randomly 2) Calculate thefitness(Xi) (i=1,2,…,N) 3) Initialize the Memory of each crow 4) H[0,1,…,3n-1] ← QuickSort(pi/wi) 5) whileiter 6) fori=1 toN 7) Select cowjrandomly 8) ifrj≥APj,iter 9) Apply difference strategy to calulateXi,iter+1 10) else 11) Xi,iter+1←a random position 12) endif 13) RepairXiusing NROA and calculatefitness(Xi) 14) Update Memory of crowi 15) endfor 16) endwhile 17) return(Mbest,f(Mbest)) 算法4中,交叉概率Cr=0.5。易知,算法的时间复杂度O(nN)+O(nlogn)+O(n)+itermax*(N*(O(n)+O(n)+O(n))=O(n3),即DECSA是一个复杂度为多项式时间的进化算法。 求解D{0-1}KP时,把Lévy飞行和差分策略都与CSA相结合,得到基于Lévy飞行的差分乌鸦搜索算法(Differential Crow Search Algorithm based on Lévy flight, LDECSA),描述如下。 算法5LDECSA。 输入参数N,n,itermax,AP,fl,a,Cr; 输出最优解Mbest及其目标函数值f(Mbest)。 1) Initialize crowsXi(i=1,2,…,N) randomly 2) Calculate the fitness(Xi) (i=1,2,…,N) 3) Initialize the Memory of each crow 4) H[0,1,…,3n-1]←QuickSort(pi/wi) 5) whileiter 6) fori=1 toN 7) Select a cowjrandomly 8) ifrj≥APj,iter 9) Apply difference strategy to calculateXi,iter+1 10) else 11) Xi,iter+1←a random position 12) endif 13) if rand()>0.5 14) Crowido Lévy flight 15) endif 16) RepairXiusing NROA and calculatefitness(Xi) 17) Update Memory of crowi 18) endfor 19) endwhile 20) return(Mbest,f(Mbest)) 易知,算法5的时间复杂度为O(nN)+O(nlogn)+O(n)+itermax*(N*(O(n)+O(n)+O(n)+O(n)))=O(n3),因此LDECSA也是一个复杂度为多项式时间的进化算法。 本文实验所用计算机的硬件配置为Intel Core i3- 4005u CPU- 1.70 GHz,4 GB 内存(3.75 GB 可用),操作系统为Windows 7(64位),C语言编程,Matlab绘图。 计算所使用的四类大规模实例[7]为不相关实例(Uncorrelated instances of D{0-1}KP, UDKP)、弱相关实例(Weakly correlated instances of D{0-1}KP, WDKP)、强相关实例(Strongly correlated instances of D{0-1}KP, SDKP)和逆向强相关实例(Inversestrongly correlated instances of D{0-1}KP, IDKP),每一类实例包含10个实例,实例规模3n∈{300,600,900,…,3 000},实例的具体数据请参考文献[7]。 首先,不同算法在不同参数fl和AP下独立运行若干实例30次,分析其计算结果所对应的箱线图确定fl和AP的合理取值;然后通过实验确定采用的差分算子形式;最后利用四类D{0-1}KP 实例的计算结果比较 SecEGA[7]、SecBFO[9]、CSA、DECSA、LCSA和LDECSA的求解性能。 在实验中,fl∈{1.0,2.0,3.0,4.0,5.0},AP∈{0.1,0.2,0.3,0.4} ,因此(fl,AP)共20种不同的组合,所有组合的ID值见表1。下面对每一组(fl,AP)进行实验以确定fl和AP的合理取值。限于篇幅,针对每一种组合形式,仅给出CSA和LCSA两种算法在规模为3n=900的实例UDKP3、WDKP3、SDKP3和IDKP3的计算结果及其所对应的箱线图。 表1 (fl,AP)及其IDTab. 1 (fl,AP) and its ID 图1是(fl,AP)在20种组合情况下独立运行CSA 30次求解UDKP3、WDKP3、SDKP3和IDKP3四个实例的最好值比较。由图1(a)可知,求解UDKP3实例,ID=9时所求最优值和平均值都最好;由图1(b)可知,求解WDKP3实例,ID=16时所求最优值最好,但ID=15时平均值最好;由图1(c)可知,求解SDKP3实例,ID=1时所求最优值最好,ID=6时所求平均值最好;由图1(d)可知,求解IDKP3实例,ID=10时所求最优值最好,ID=8时所求平均值最好。本文采用的是取得平均值最好的组合。DECSA和CSA采用相同的参数。 图2是(fl,AP)在20种组合情况下独立运行LCSA 30次求解UDKP3、WDKP3、SDKP3和IDKP3四个实例的最好值比较。由图2可知,求解四个实例时,很多组合所求的最优值相同,在此,选取ID=3即AP=0.1,fl=3的组合形式。LDECSA和LCSA采用相同的参数。 图1 CSA求解四个实例的性能比较Fig. 1 Performance comparison of CSA for solving 4 instances 图2 LCSA求解四个实例的性能比较Fig. 2 Performance comparison of LCSA for solving 4 instances 差分算子为DE/best/1/Bin或DE/best/1/Exp,记DE/best/1/Bin的ID为1,DE/best/1/Exp的ID为2。下面分别对两种差分算子进行实验,以确定合理的差分算子。限于篇幅,仅给出DECSA和LDECSA在规模为3n=900的实例UDKP3、WDKP3、SDKP3和IDKP3独立运行30次的计算结果及其所对应的箱线图。由图3、4可以看出,DECSA和LDECSA都是ID为1时的差分算子能获得更好的最优解,故均采用DE/best/1/Bin形式的差分算子。 图3 DECSA在两种差分算子下的求解实例比较Fig. 3 Comparative results of DECSA with two differential operators 图4 LDECSA在两种差分算子下求解实例比较Fig. 4 Comparative results of LDECSA with two differential operators 求解四类D{0-1}KP实例时,设置参数N=40,itermax=500。其中,CSA和DECSA求解UDKP类实例时,AP=0.2,fl=4;求解WDKP类实例时,AP=0.3,fl=5;求解SDKP类实例时,AP=0.2,fl=1;求解IDKP类实例时,AP=0.2,fl=3。LCSA和LDECSA求解四类D{0-1}KP实例时,AP=0.1,fl=3.0;DECSA和LDECSA中差分算子为DE/best/1/Bin,交叉概率Cr=0.5。结果见表2~5,其中动态规划法求解D{0-1}KP(Dynamic programming based algorithms for the discounted {0-1} Knapsack Problem, DPDKP)的数据来自文献[6],SecEGA算法的计算结果来自文献[7],SecBFO算法的计算结果来自文献[9],CSA、DECSA、LCSA和LDECSA的计算结果均为算法独立运行30次所得。 由表2的数据分析得到图5,Opt/Best和Opt/Mean分别得到最好值近似比和平均值近似比[7]。图5(a)为求解UDKP类实例时6种算法的最好近似比值比较图,其中CSA和DECSA的求解性能最差,SecEGA的求解性能较差,这三个算法的最优近似比值在1.1~1.25;SecBFO、LCSA和LDECSA的求解性能较前三者要好,LDECSA最好,LCSA比LDECSA稍差,比SecBFO稍好,这三个算法的近似比值在1.0~1.025。图5(b)为求解UDKP类实例时6种算法的平均近似比值比较图,与图5(a)相比,CSA和DECSA基本重合,其他算法变化不大。 由图5还可以看出,差分策略在解质量不高的情况下,效果并不好,在解质量较高的情况下,能提高最优解的质量。在图5(b)中,应用了差分策略的DECSA比CSA也仅仅在UDKP2和UDKP3上效果好一点,其余实例不如CSA或两个算法求解性能相当;而LCSA本身能获得较好的最优解,应用了差分策略后,LDECSA所获得的最优解进一步得到优化,但优化能力有限,故LDECSA的性能比LCSA好,但差别不大。 由表3的数据分析得到图6。图6(a)为求解WDKP类实例时6种算法的最好值近似比比较图,其中CSA和DECSA的求解性能最差,且随着问题规模的增大,近似比值增大,说明求解质量下降;LDECSA、LCSA、SecEGA和SecBFO四种算法近似比值都在1.0~1.01,且LDECSA最优,最优近似比值几乎为1,LCSA次之,SecEGA和SecBFO稍差。图6(b)为求解WDKP类实例时6种算法的平均近似比值比较图,与图6(a)相比,CSA和DECSA几乎重合,求解性能仍然是最差,SecEGA平均性能下降,明显不如SecBFO、LCSA和LDECSA,LDECSA的平均求解性能最优。 表2 求解UDKP实例的结果比较Tab. 2 Results comparison for solving UDKP instances 图5 求解UDKP类实例的近似比比较Fig. 5 Comparison of approximate ratio for solving UDKP instances 由表4的数据分析得到图7。图7(a)为求解SDKP实例时6种算法的最好值近似比比较图,其中CSA和DECSA的求解性能最差,且随着问题规模的增大,近似比值逐渐增大,LDECSA近似比值最小,接近1,LCSA比LDECSA略差,SecEGA和SecBFO比LCSA稍差,且在大部分实例上两种算法求解能力相当,仅在求解SDKP4和SDKP7时,SecEGA不如SecBFO。图7(b)为求解SDKP实例时6种算法的平均近似比值比较图,与图7(a)相比,CSA和DECSA几乎重合,求解性能仍然是最差,SecEGA平均求解性能下降,明显不如SecBFO,LDECSA的平均求解性能最优。 由表5的数据分析得到图8。图8(a)为求解IDKP类实例时6种算法的最优近似比值比较图,其中CSA和DECSA的求解性能最差,且随着问题规模的增大,近似比值逐渐增大,其余四种算法求解能力相当,能求得近似最优解或最优解。图8(b)为求解IDKP类实例时6种算法的平均近似比值比较图,跟图8(a)相比,CSA和DECSA几乎重合,求解性能仍然最差,SecEGA变化明显,求解性能下降,SecBFO仅在求解IDKP2时性能略有下降,LCSA和LDECSA基本重合,由表5也可以看出,两种算法所得数据差别不大,求解性能最优。 由图5~8可以看出, LCSA的求解性能明显比DECSA要好,LDECSA的求解性能比LCSA要好,因此,在求解四类D{0-1}KP实例时,Lévy飞行能有效地改进CSA,差分策略能辅助Lévy飞行策略取得更令人满意的近似解或最优解。 图9为LDECSA在求解四类D{0-1}KP实例时最优近似比比较的箱线图。由图9可以看出,LDECSA在求解IDKP时,性能最佳,近似比值接近1,10个实例基本能得到最优解或近似最优解;LDECSA在求解WDKP时,性能较好,近似比值稍微大于1,能获得较满意解;LDECSA在求解SDKP时,近似比值都在1.005以下;相比较而言,LDECSA求解UDKP时性能较差。这也说明,LDECSA不能同时满足四类实例都获得最优解或近似最优解。 表3 求解WDKP实例的结果比较Tab. 3 Results comparison for solving WDKP instances 图6 求解WDKP类实例的近似比比较Fig. 6 Comparison of approximate ratio for solving WDKP instances 表4 求解SDKP实例的结果比较Tab. 4 Results comparison for solving SDKP instances 图7 求解SDKP类实例的近似比比较Fig. 7 Comparison of approximate ratio for solving SDKP instances 表5 求解IDKP实例的结果比较Tab. 5 Results comparison for solving IDKP instances 图8 求解IDKP类实例的近似比比较Fig. 8 Approximate ratio for solving IDKP instances 为了进一步验证算法LDECSA的求解性能,取其最好值与基于差分策略的混沌乌鸦算法(Chaotic Crow Search Algorithm based on Differential Evolution strategy,DECCSA)[17]进行比较,DECCSA的计算结果参照文献[17],比较结果如图10所示。由图10(a)可以看出,对UDKP类实例,LDECSA的求解性能更佳,近似比值不大于1.02,DECCSA的近似比值在1.02~1.15;由图10(b)可知,LDECSA的求解性能更佳,近似比值不大于1.001,DECCSA的近似比值在1.00~1.006;由图10(c)可知,LDECSA的求解性能更佳,近似比值不大于1.003,DECCSA的近似比值在1.003~1.02;由图10(d)可知,对于IDKP类实例,算法DECCSA和LDECSA各有优劣,近似比值基本等于1,差别不大。总的来说,算法LDECSA优于DECCSA。 综上所述:对于大规模的四类 D{0-1}KP 实例,LCSA和LDECSA均能够快速求得一个近似比接近于1的近似解,且LDECSA的求解性能比LCSA更好,因此LDECSA是适于求解大规模难D{0-1}KP 的有效且实用的进化算法。 图9 LDECSA在四类实例上的最好值近似比比较Fig. 9 Best approximate ratio comparison of LDECSA on 4 kinds of instances 图10 LDECSA和DECCSA的最好值近似比比较Fig. 10 Best approximate ratio comparison of LDECSA and DECCSA 乌鸦搜索算法是一种新颖的模拟乌鸦搜索食物的演化算法,D{0-1}KP 是新型的{0-1}KP,有三种数学模型,本文研究的是如何利用改进的乌鸦搜索算法求解第二数学模型的D{0-1}KP。在此,乌鸦个体采用整数向量编码方式,并采用新的贪心策略修复和优化非正常编码个体;为了避免CSA中的乌鸦个体过早地陷入局部最优,在算法中引入Lévy飞行;为了提高收敛速度,在算法中引入差分策略。仿真实验表明:对于大规模的D{0-1}KP 实例,LDECSA能够快速求得一个近似比接近于 1的近似解,因此非常适合求解大规模D{0-1}KP。 由于LDECSA在四类实例上的求解性能不尽相同,如何针对UDKP类实例设计出更有效的算法是下一步的研究内容。此外,由于CSA提出的时间较短,该算法的应用还很少,如何把CSA应用到其他领域中也是一个值得研究的问题。 参考文献: [1]FAYARD D, PLATEAU G. Resolution of the 0- 1 knapsack problem: comparison of methods [J]. Mathematical Programming, 1975, 8(1): 272-307. [2]CHU P C, BEASLEY J E. A genetic algorithm for the multidimensional knapsack problem [J]. Journal of Heuristics, 1998, 4(1): 63-86. [3]CHEN Y, HAO J-K. An iterated “hyperplane exploration” approach for the quadratic knapsack problem [J]. Computers & Operations Research, 2017, 77: 226-239. [4]HILEY A, JULSTROM B A. The quadratic multiple knapsack problem and three heuristic approaches to it [C]// GECCO ’06: Proceedings of the 8th Annual Conference on Genetic and Evolutionary Computation. New York: ACM, 2006: 547-552. [5]GULDAN B. Heuristic and exact algorithms for discounted knapsack problems [D]. Erlangen and Nuremberg, Bavaria, Germany: University of Erlangen-Nürnberg, 2007: 1-78. [6]RONG A, FIGUEIRA J R, KLAMROTH K. Dynamic programming based algorithms for the discounted {0-1} knapsack problem [J]. Applied Mathematics and Computation, 2012, 218(12): 6921-6933. [7]贺毅朝,王熙照,李文斌,等.基于遗传算法求解折扣{0-1}背包问题的研究[J].计算机学报,2016,39(12):2614-2630. (HE Y C, WANG X Z, LI W B, et al. Research on genetic algorithms for the discounted {0-1} knapsack problem [J]. Chinese Journal of Computers, 2016, 39(12): 2614-2630.) [8]HE Y-C, WANG X-Z, HE Y-L, et al. Exact and approximate algorithms for discounted {0-1} knapsack problem [J]. Information Sciences, 2016, 369: 634-647. [9]刘雪静,贺毅朝,吴聪聪,等.基于细菌觅食算法求解折扣{0-1}背包问题的研究[J/OL]. 计算机工程与应用 (2017- 02- 16) [2017- 08- 30]. http://kns.cnki.net/kcms/detail/11.2127.TP.20170216.1044.038.html. (LIU X J, HE Y C, WU C C, et al. Research on bacterial foraging optimization algorithm for the discounted {0-1} knapsack problem [J/OL]. Computer Engineering and Applications (2017- 02- 16) [2017- 08- 18]. http://kns.cnki.net/kcms/detail/11.2127.TP.20170216.1044.038.html.) [10]吴聪聪,贺毅朝,陈嶷瑛,等.变异蝙蝠算法求解折扣{0-1}背包问题[J].计算机应用,2017,37(5):1292-1299. (WU C C, HE Y C, CHEN Y Y, et al. Mutated bat algorithm for solving the discounted {0-1}KP [J]. Journal of Computer Applications, 2017, 37(5): 1292-1299.) [11]ZHU H, HE Y, WANG X, et al. Discrete differential evolutions for the discounted {0-1} knapsack problem [J]. International Journal of Bio-inspired Computation, 2017, 10(4): 219-238. [12]ASKARZADEH A. A novel metaheuristic method for solving constrained engineering optimization problems: crow search algorithm [J]. Computers & Structures, 2016, 169: 1-12. [13]贺毅朝,王熙照,寇应展.一种具有混合编码的二进制差分演化算法[J].计算机研究与发展,2007,44(9):1476-1484. (HE Y C,WANG X Z, KOU Y Z. A binary differential evolution algorithm with hybrid encoding [J]. Journal of Computer Research and Development, 2007, 44(9): 1467-1484.) [14]REYNOLDS A M. Cooperative random Lévy flight searches and the flight patterns of honeybees [J]. Physics Letters A, 2006, 354(5/6): 384-388. [15]YANG X-S, DEB S. Cuckoo search via Lévy flights [C]// NaBIC 2009: Proceedings of the 2009 World Congress on Nature & Biologically Inspired Computing. Piscataway, NJ: IEEE, 2009: 210-214. [16]NOMAN N, IBA H. Enhancing differential evolution performance with local search for high dimensional function optimization [C]// GECCO ’05: Proceedings of the 7th Annual Conference on Genetic and Evolutionary Computation. New York: ACM, 2005: 967-974. [17]刘雪静,贺毅朝,路凤佳,等.基于差分策略的混沌乌鸦算法求解折扣{0-1}背包问题[J].计算机应用,2018,38(1):137-145. (LIU X J, HE Y C, LU F J, et al, Chaotic crow search algorithm based on differential evolution strategy for solving discount {0-1} knapsack problem [J]. Journal of Computer Applications, 2018, 38(1): 137-145.)3 改进的CSA求解D{0-1}KP
3.1 混合编码方式
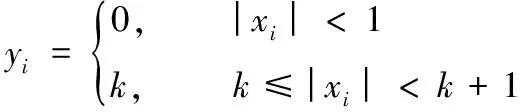
3.2 新的贪心修复与优化算法
3.3 基于Lévy飞行的CSA
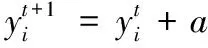
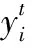
3.4 基于差分的CSA求解D{0-1}KP
3.5 基于Lévy 飞行的DECSA求解D{0-1}KP
4 仿真实验与分析
4.1 确定AP和fl的值
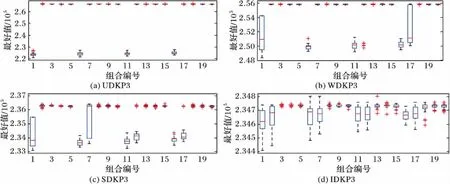
4.2 差分策略的选择

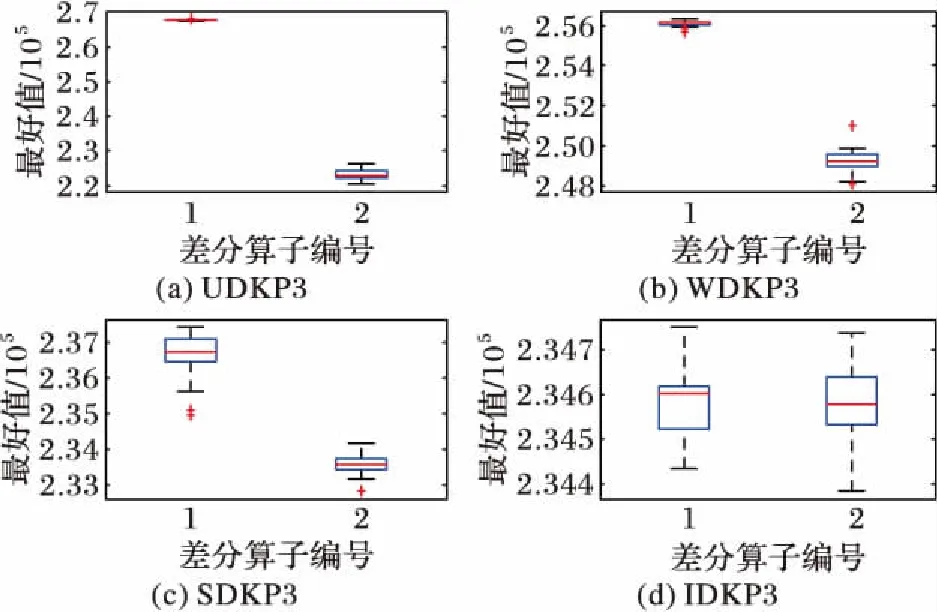
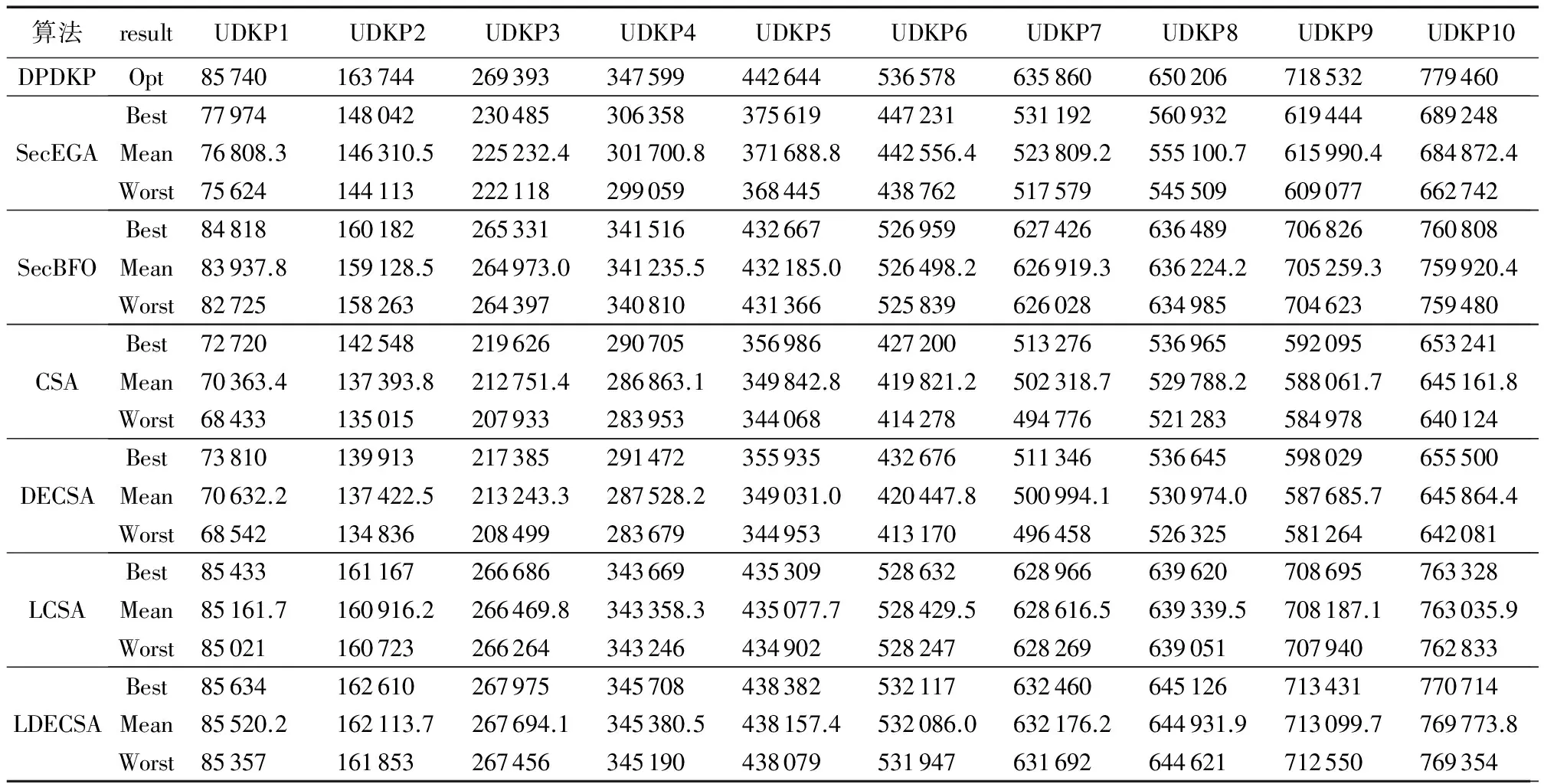
4.3 仿真实验结果

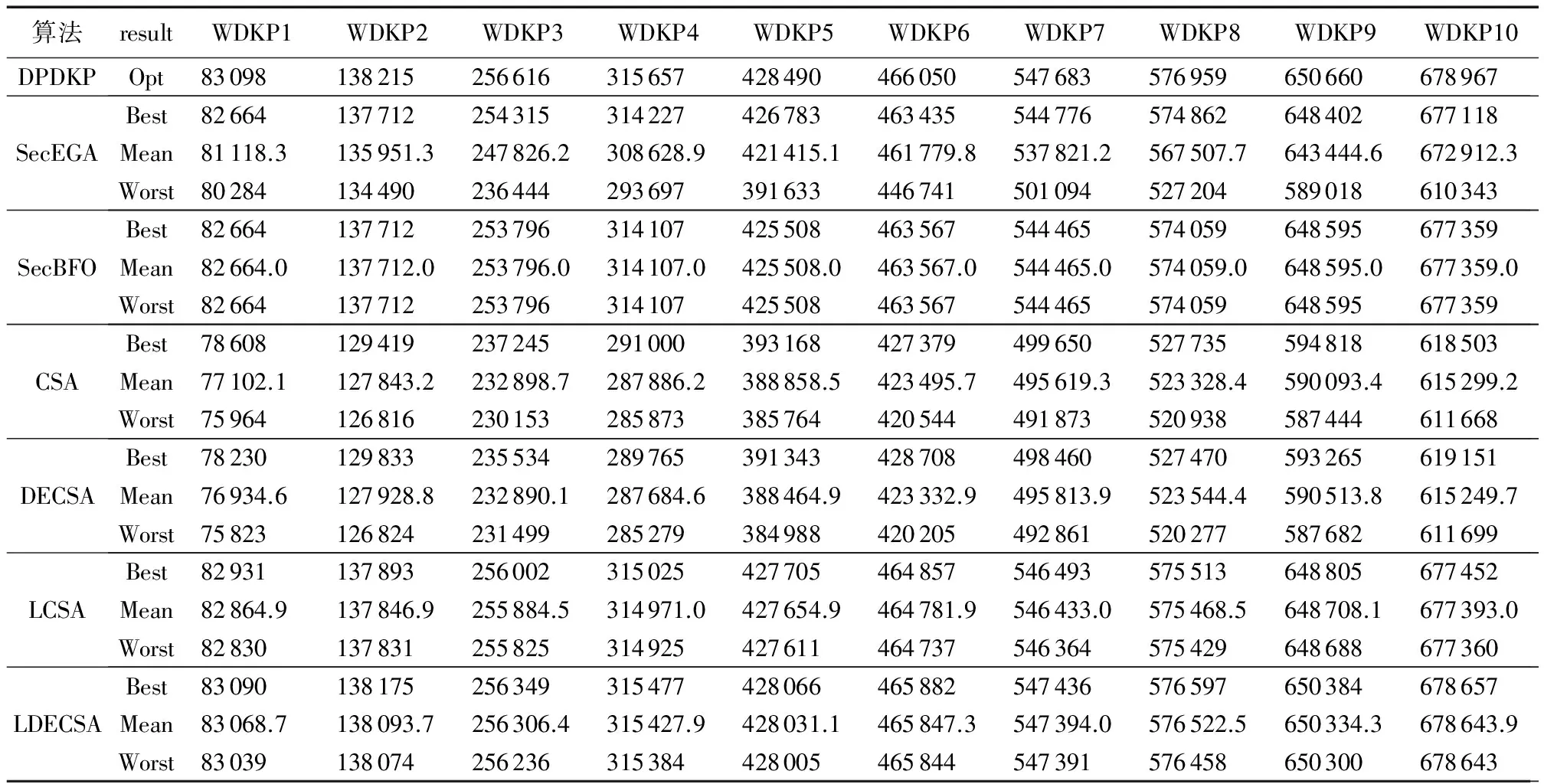

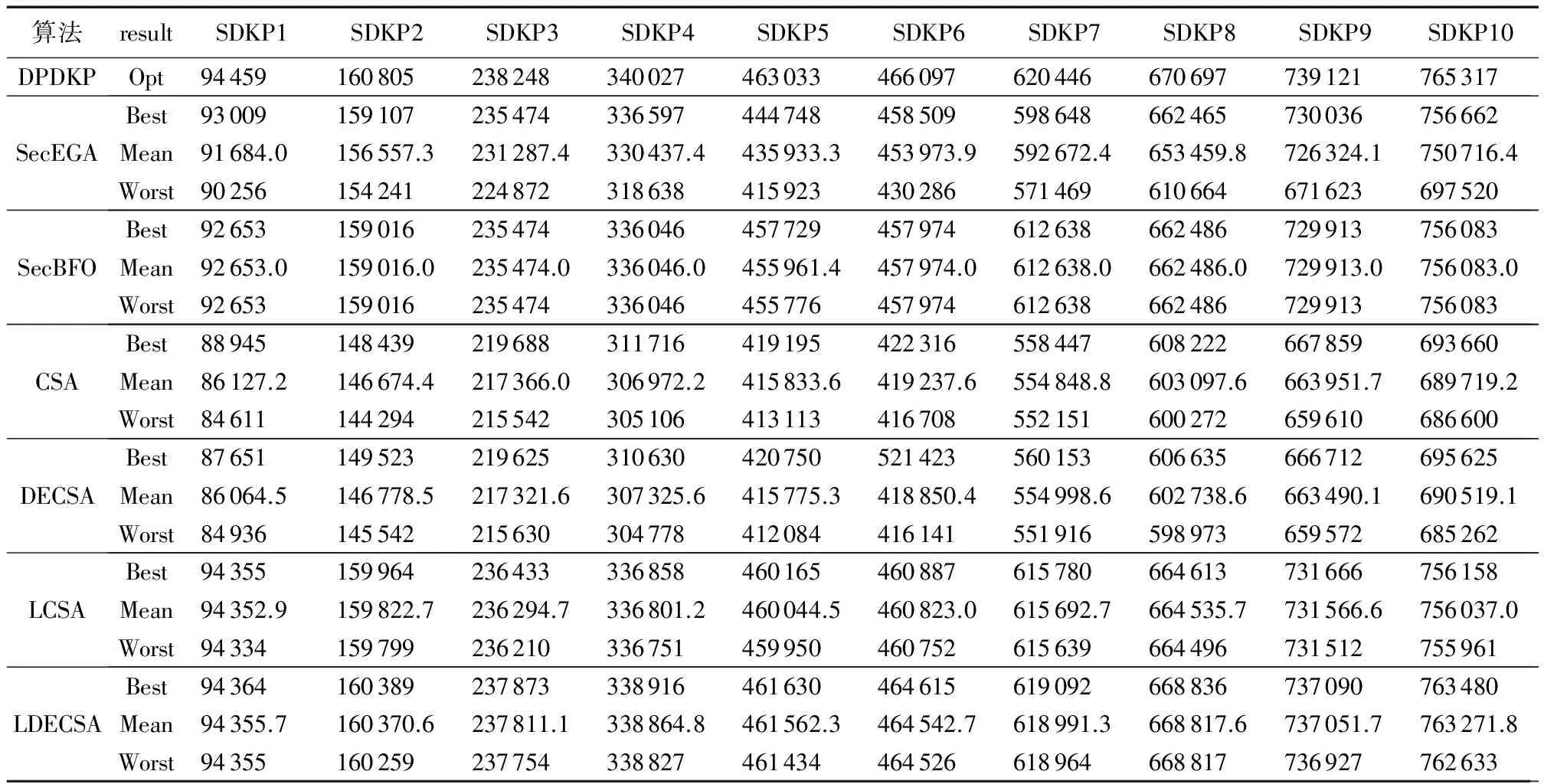


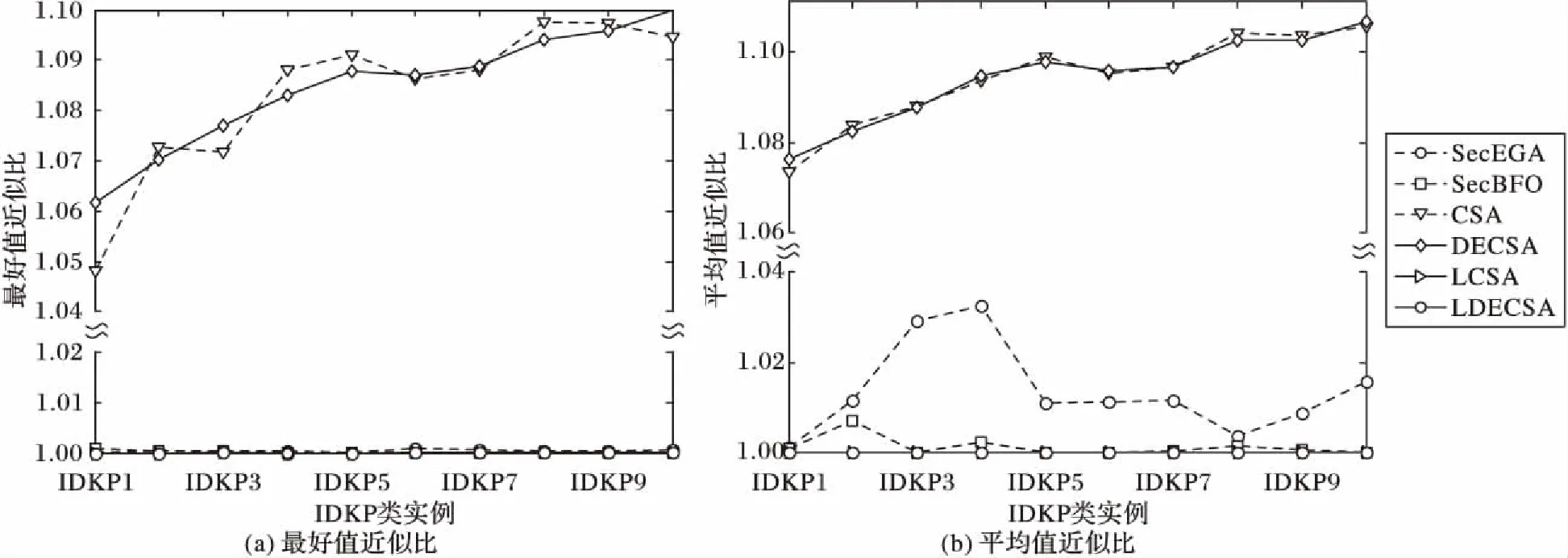
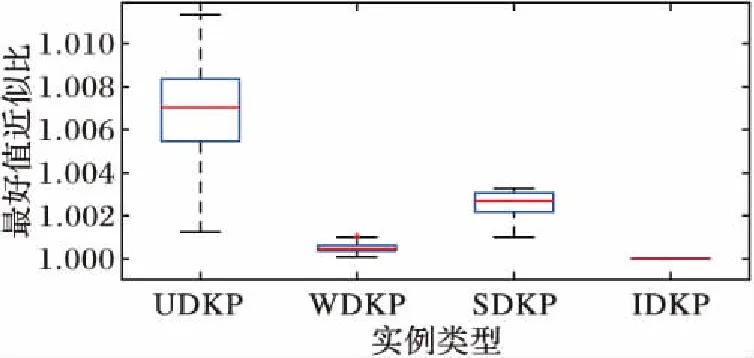
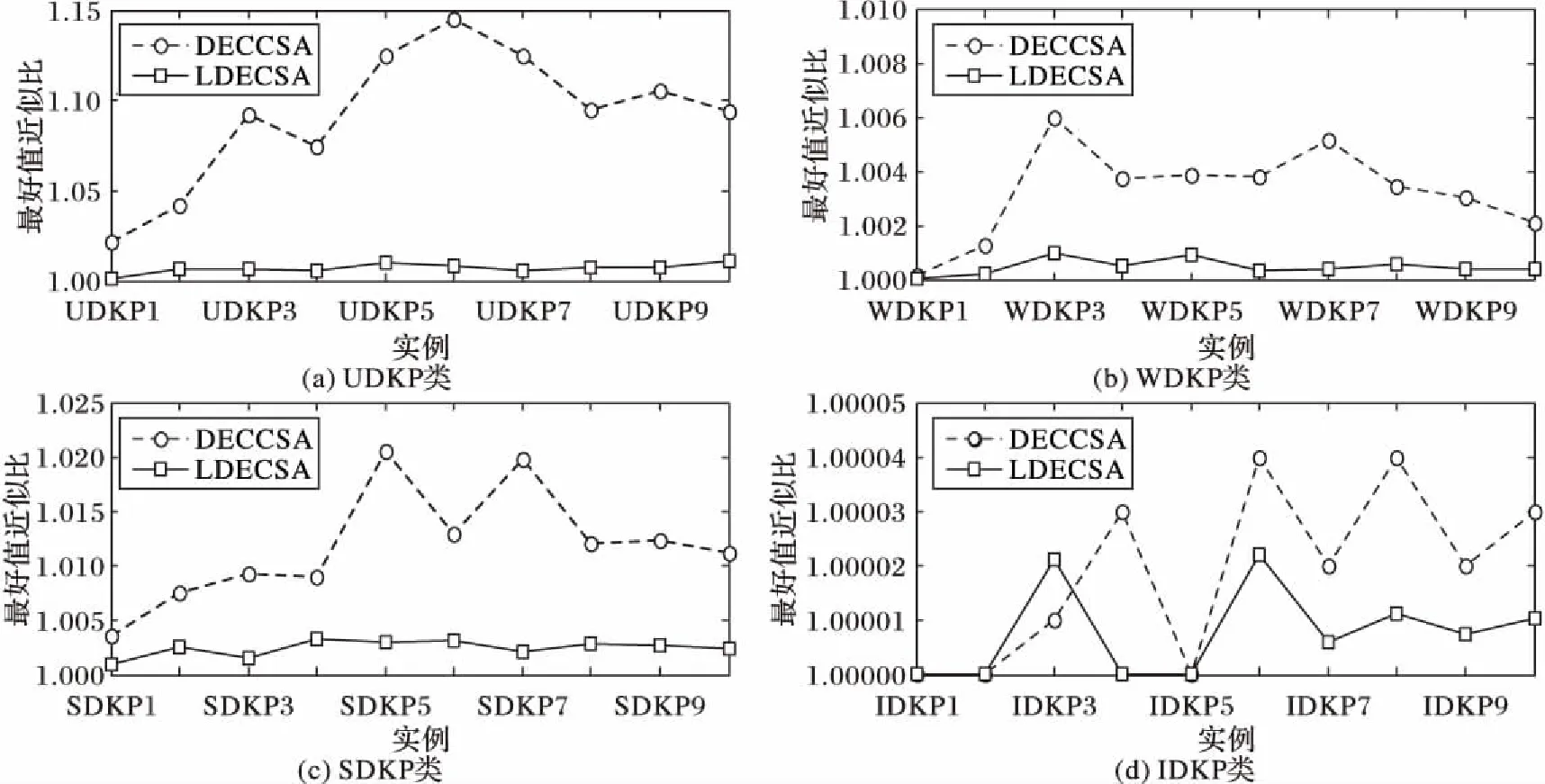
5 结语

