时空众包环境下基于统计预测的自适应阈值算法

刘　辉，李盛恩

(山东建筑大学 计算机科学与技术学院，济南 250101)(*通信作者电子邮箱megatron101@163.com)

0　引言

“众包”这一概念是由Jeff Howe提出的，旨在帮助机构把一些工作交给互联网用户。早期的众包平台包括Amazon’s Mechanical Turk、CrowdFlower，需要互联网用户利用个人计算机完成相应的任务。近几年，移动智能设备的快速普及极大地促进了移动互联网的发展，众包平台也逐渐得到了业界和大众的关注，例如滴滴打车、饿了么等应用。因此，众包平台正式从传统众包发展成为时空众包。与传统众包的研究类似，时空众包同样专注于任务分配。移动智能设备携带了用户的个人信息如位置、手机号码等，任务请求者将个人信息及具体任务提交到平台，平台在掌握任务及工人信息的情况下，选出合适工人去完成任务请求者的任务，并得到报酬。因此如何将随机出现并带有时间、位置信息的任务分配给最合适的工人并使报酬最大化成为时空众包环境下要解决的问题。本文以一类新型时空众包平台应用南瓜车为例，在分析贪心算法和随机阈值算法的基础上，设计一种基于统计预测的自适应阈值算法。

1　相关研究

1.1　问题定义

本章介绍任务分配算法中涉及到的实体对象及评价标准，并举例阐述实现任务分配的具体过程。

1)众包任务t。t为任务请求者通过移动智能设备向平台发出的任务请求，可定义为t={Pt,Rt,St,Et,Mt}。其中：Pt、Rt代表t出现的位置和活动范围；St、Et代表t的上线时间和下线时间，若在此时间段内t得不到分配，则用户下线；Mt是任务t的回报。

2)众包工作地点p。p为任务执行的地点，可定义为p={Pp,Sp,Ep,Cp}。其中：Pp代表p出现的位置；Sp、Ep分别代表p的上线时间和下线时间；Cp是地点p的容量，即能够容纳Cp个任务在p执行。

3)众包工人w。w可定义为w={Pw,Rw,Sw,Ew,Qw}。其中：Pw、Rw是w出现的位置和活动范围；Sw、Ew代表w的上线时间和下线时间；Qw是w的工作质量。

4)效用。效用定义为U(t,w,p)=Mt*Qw，即若任务t和工人w得以分配，则效用为任务回报和工人工作质量的乘积。

在线任务分配包括三类对象：任务t、工作地点p、工人w依时间次序出现，众包平台在任意时刻根据任务分配算法对此时刻已出现的t∈T，p∈P，w∈W进行匹配(T、P、W为已出现且未进行匹配的任务、地点和工人的集合)，最终使效用总和最大化。

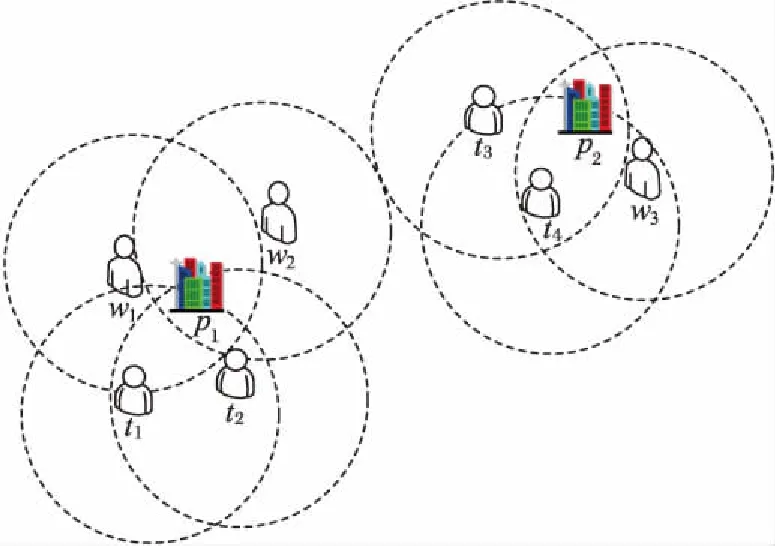
图1　任务、地点和工人分布示意图Fig. 1　Task, position and worker distribution diagram

1.2　系统分配任务模式下的任务分配

无论是有两类对象的众包平台，还是有三类对象在线分配的新型众包平台，都涉及到了任务分配问题。根据时空众包任务分配科技报告[1],时空众包平台的任务分配有两种不同的模式：工人选择任务(Worker Selected Tasks, WST)和系统分配任务(Server Assigned Tasks, SAT)。WST模式是在线工人不通过众包平台分配而自主选择任务请求者发出的任务的工作模式，因此众包平台不能控制任务分配使总效用达到最优，故WST模式不属于本文研究的重点。以下将介绍SAT模式下两种对实时性要求不同的任务分配问题：离线任务分配与在线任务分配。

1.2.1离线分配

离线任务分配问题是传统众包中的经典问题，其中最具有代表性的微任务平台如Amazon’s Mechanical Turk[2]，文献[2]中阐述了传统众包平台可以解决的图像识别、信息检索、自然语言处理及专家系统等，该平台为最早的离线分配模型。

随着传统众包的发展，离线分配问题可以根据待分配对象的数量分为两类：离线二分匹配和离线三分匹配。长期以来，离线二分匹配一直都是组合优化领域的经典问题，可以看作对一个无向图G=(U∪V,E)求E的子集M的过程。离线二分匹配可以根据边是否有权重分为最大二分匹配和最大二分加权匹配[3]，分别对应众包领域中的两个优化目标：最大化任务分配数和最大化效用值。针对这两个不同的优化目标，文献[3]分别介绍了Ford-Fulkerson算法和Hungarian算法。文献[4-5]为了将二分图匹配问题扩展到空间数据中，把离线分配问题看作等价于空间匹配问题的一个变种问题。针对空间数据的任务分配，文献[4，6]针对移动距离进行了研究，文献[4]的优化目标是基于有容量限制的条件下，最小化匹配的距离之和，而文献[6]的优化目标为最小化最大匹配距离。文献[7]均提出了两段式分配策略，不同之处在于文献[7]将整个分配过程平均为两个部分，前后两个部分分别采用贪心思想和Hungarian算法解决图匹配问题，而文献[8]则在得到初始分配后，在保持分配稳定的基础上维护分配的最优性。与离线二分匹配问题不同，最大三分匹配为NP-hard问题[9]，可利用局部搜索的思想去尝试获得更好的结果。

1.2.2在线分配

在SAT模式中，在线分配问题不仅存在优化目标的不同，也存在待分配对象类别和数量的区别。文献[8]认为对象的出现顺序能够影响分配算法的性能，已存在的研究中都在讨论最坏情况下的算法性能，但研究发现最坏情况的出现概率非常低，如果参与对象的数量是n的话，则最坏情况出现的概率为1/n!，故研究在最坏情况下的算法性能意义并不大，应讨论算法在大多数情况下的平均性能，并提出了竞争比的概念。根据文献[10]，在线任务分配可以规约为有权双向图匹配问题，文献[11-12]分别利用贪心算法解决此问题，使竞争比达到了1/2。文献[5]中先把任务分配问题规约为稳定婚姻问题和最近点问题，然后提出了一种针对无权双向图匹配的Chain算法，并在有权图上进行了改进。该算法首先随机选取一个待分配的对象O作为初始点寻找可与之匹配且最近邻的其他类对象Y，再寻找Y的其他最近邻的对象，以此类推。文献[6]提出了关于距离的阈值算法，只有移动距离小于d的对象才会得到匹配。文献[13]针对两类对象的在线分配，以最大化任务分配数为优化目标，但只允许一类对象动态出现，对解决在线的最大二分匹配问题提出了新的思路。文献[8]改进了贪心算法加入阈值限制条件，并提出了两段式全局在线分配算法，根据对问题规模的估计，在任务分配过程中，前半段采用贪心的策略为每个新出现的任务(工人)分配可能得到最高效用的工人(任务)，后半段使用Hungarian算法对有权双向图进行匹配。文献[14]改进了阈值算法，提出了自适应阈值算法，该算法能够根据任务分配情况自动调整阈值的大小。

1.3　其他相关工作

为保持众包平台参与人员的数量,文献[15]提出一套积分管理策略，在对众包参与者的吸引及众包工人的工作质量上有一定的帮助。文献[16]通过反转竞拍、游戏化、经验值更新等策略激励众包参与者和吸引更多的众包参与者。文献[17]提出一种基于多种任务的主题感知任务分配策略，根据任务的类型分配擅长该类型任务的众包工人。

基于以上研究可以发现，在各类阈值算法中，虽然通过设置阈值可以过滤掉效用较小的分配对，但仅仅设置阈值往往还不能使结果接近最优，必须有相应的匹配策略来调度。基于此，本文提出一种基于统计预测的自适应阈值算法和匹配策略。实验表明，该算法能够在真实情况下使总效用接近最优，算法整体表现优于贪心算法和随机阈值算法。

2　阈值算法与匹配策略

2.1　贪心算法

文献[14]中称贪心算法为朴素随机算法，意为对每一个新出现的对象，如果通过这个对象可以作出若干任务分配，则从任务分配集中随机选择一种分配。算法的输入为新出现的对象，包括任务、工人、工作地点以及效用函数；算法的输出为分配结果。当新对象出现时，算法会在候选队列中随机选择满足约束条件的匹配对象。如果得到的匹配结果不为空，则把新出现的对象和匹配到的对象加入到分配结果，并把匹配对象从候选队列中移除，停止查找；如果匹配对象为空，则把新出现的对象加入到候选队列中。

算法1贪心算法。

输入随机出现的任务、工人、工作地点及效用函数。

对每一个新出现的任务、工人及工作地点v：

1)根据出现对象的类型，在候选队列中选择满足约束的其他两类对象:o1,o2←Cand。

2)若o1,o2不为空，则将v与o1,o2进行匹配，得到匹配结果:M←{v,o1,o2}。

3)若o1,o2为空，则将v加入候选队列:Cand←v。输出匹配结果M。

贪心算法虽时间消耗比较小，但是由于任务、地点、工人完全是按照出现顺序进行分配，没有考虑效用的大小，所以在不同回报的任务出现冲突时，贪心算法会按照出现顺序选择待分配对象。若回报较低的任务先出现并且满足分配条件时，后出现的较高回报的任务将无法得到分配。

2.2　随机阈值算法

随机阈值算法是改进的贪心算法，对新出现的对象,除需要对象满足基本的活动范围条件外，还需满足阈值条件即该分配产生的效用应大于随机阈值。如算法2所示，在算法第1)步，首先阈值设置为ek，k为随机选择0～θ的值，θ的取值为：

θ=「ln(Umax+1)⎤

(1)

其中Umax是从任务分配过程中单个分配可能获得的最大效用，可以从历史分配数据中获得。在候选队列中随机选择一个满足约束条件且满足产生的效用大于阈值的匹配对象。如果匹配对象不为空，则加入分配结果，然后从候选队列中移除匹配对象，停止查找；否则把新对象加入到候选队列中。最后返回分配结果。

算法2随机阈值算法。

输入随机出现的任务、工人、工作地点及效用函数。

对每一个新出现的任务、工人及工作地点v：

1)随机设置阈值ek:k∈[0,θ]，θ=「ln(Umax+1)⎤。

2)根据出现对象的类型,在候选队列中选择满足约束且产生效用大于阈值的其他两类对象:o1,o2←Cand。

3)若o1,o2不为空，则将v与o1,o2进行匹配，得到匹配结果:M←{v,o1,o2}。

4)若o1,o2为空，则将v加入候选队列:Cand←v。输出匹配结果M。

尽管随机阈值算法能够在一定程度上过滤掉效用较低的任务分配，但是由于k值的选择是随机的，所以算法总效用差异较大，表现不稳定。

2.3　基于统计预测的自适应阈值算法

在阈值算法中，三类对象可以分配的前提是满足一定的阈值条件。阈值的设置关键之处在于：若阈值设置过低，无法起到过滤作用，使整个分配过程与贪心算法类似且计算量增多；若阈值设置过高，大部分对象无法正常参与分配，浪费平台总效用。为解决阈值的设置问题，本文提出一种基于统计预测的自适应阈值算法，算法思想如下。

2.3.1阈值作用对象

在贪心算法和随机阈值算法中，阈值通常是针对效用设置的，有如下缺点：1)阈值产生作用的前提是对任务进行预分配得到效用值，根据该效用值是否满足阈值条件决定该分配是否有效，若未满足阈值条件则考虑其他分配，这种局部搜索方法造成的时间消耗会使任务分配的等待时间变长；2)有一定的概率造成效用的浪费，例如高回报任务与低工作质量工人结合或低回报任务与高工作质量工人结合的分配方式，虽然效用值满足阈值条件，但是以上两种分配方式并不能得到理想的效用值。

为解决以上问题，本文将任务的回报值作为阈值的作用对象。当任务出现时，考察该任务的回报值，若任务回报值满足阈值条件则进入任务队列，否则丢弃掉。为任务的回报设置阈值有以下优势：1)如图2所示，在任务出现时，按照阈值大小可直接决定此任务是否可加入任务队列，省去了局部搜索的过程，减少时间消耗并提高了分配效率；2)过滤掉回报较小的任务，能降低低回报任务与高工作质量工人分配的概率，提高众包平台整体的效用值。

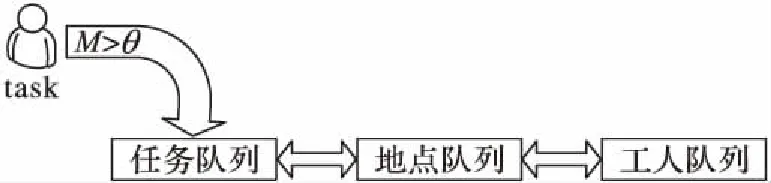
图2　阈值算法示意图Fig. 2　Threshold algorithm diagram

2.3.2阈值设置

基于统计预测的自适应阈值算法采用一种在线调整的策略，该算法的运行过程根据实时出现的任务、工人、工作地点和得到分配的对象以及超时的对象，实时统计当前平台中空闲任务(Free Task, FT)、空闲工人(Free Worker, FW)、空闲工作地点(Free Position, FP)的数量，以及最大回报值Rmax和最小回报值Rmin。根据前一时刻的阈值θ′，在调整基数∂的基础上计算出当前时刻的阈值θ。

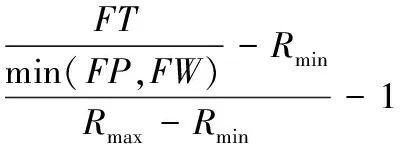
(2)

为防止阈值的波动过大导致的平台运行状态不稳定，阈值的设置应当控制在一定的范围内，本文将阈值的调整范围设置为当前时刻出现任务回报的差值，每次调整的范围为[-∂,∂]。当某时刻未出现任务或出现单个任务时，调整范围设置为1，只进行较小幅度的调整。CRmax与CRmin分别是当前时刻出现的最大回报值和最小回报值。

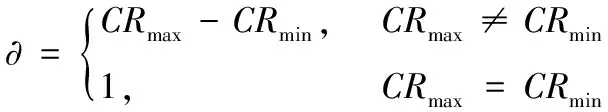
(3)

算法3基于统计预测的自适应阈值算法。

输入随机出现的任务、工人、工作地点及效用函数。

1)对每一个新出现的任务、工人及工作地点v，根据式(2)计算当前时刻的阈值。

2)根据出现对象的类型，在候选队列中选择满足约束且产生效用大于阈值的其他两类对象:o1,o2←Cand。

3)若o1,o2不为空，则将v与o1,o2进行匹配，得到匹配结果:M←{v,o1,o2}。

4)若o1,o2为空，则将v加入候选队列:Cand←v。

输出匹配结果M。

2.4　匹配策略

任务分配算法的性能及效果在很大程度上依赖数据的分布或对象出现的顺序[8]，若数据分布不均匀则算法的效果无法保证。为消除这种不确定性，本文采用“一对一”的匹配策略，在满足约束条件即待分配的对象在互相的活动范围内时，当任务回报确定时，与之匹配的工人也将确定。通过匹配策略，使平台的总效用值达到最优或接近最优。

“一对一”的匹配策略采用Min-max normalization方法为每个任务匹配工人。假设任务回报值的范围为Mt∈[0,100]，工人的工作质量Qw∈[0,1],若出现一个任务回报值为80的任务，则根据匹配策略将为其匹配一个工作质量为0.8的众包工人。匹配策略可以避免低回报任务与高工作质量工人结合或高回报值任务与低工作质量工人结合造成平台效用的浪费。

在数据分布不均匀时，采用匹配策略能够出现任务或工人的闲置问题。如图3所示，对gMission[18]数据集进行统计发现，工人的工作质量集中在0.5左右，而任务的回报值集中在80～90，回报值为90的任务与工作质量为0.5的工人都不能完全匹配到合适的对象。为解决此问题，本文把任务与工人根据其数据分布分为两个部分。通过对历史数据的分析和估计得到任务回报值的中位数α和众包工人工作质量的中位数β。当出现一个任务时，若任务的回报Mt∈[0,α]，则匹配的工人工作质量也应满足Qw∈[0,β]；若任务的回报Mt∈[α,100]，则匹配的工人工作质量也应满足Qw∈[β,1]。根据此规则，使用Min-max normalization方法寻找一个满足匹配策略的其他对象。

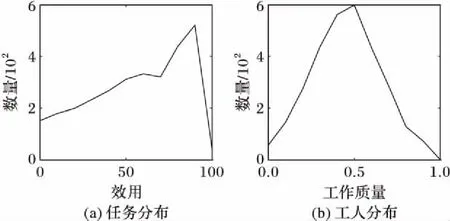
图3　gMission数据集任务回报及工人工作质量分布Fig. 3　Task return and worker quality distribution of gMission data set

而真实情况中，在匹配确定工作质量或回报的对象中，往往没有完全吻合条件的确定对象，此时可匹配近似满足条件的对象，近似对象与确定对象之间的差异不超过5%，此差异值的设置可参考众包对象的密度。

2.5　基于统计的概率预测

在2.4节中介绍了当出现一个任务t时，如何匹配满足约束条件且使效用最大化的工人w。本节主要讲述计算工人w会在任务t的活动时间内出现的概率，按照概率决定任务t是否等待工人w。

在历史数据中可以得到在整个众包活动周期中可与任务t匹配的工人w的数量，通过对多组数据的学习可以得到一个估值。任务t的生命周期有时长限制，可计算出在任务t的生命周期内可以出现的工人w的数量。由于众包平台任务及工人的出现受客观因素影响较大，故在任务t的生命周期内可以通过匹配策略匹配到工人w的概率是：

(4)

其中β是在不同环境下客观因素对众包平台的影响指数，如天气、节假日等。当p(t,w)≥θ，即在任务t的生命周期内匹配到工人w的概率大于θ时，任务t选择等待工人w；反之，则不等待。

在估计任务t匹配到工人w的概率的同时，为该类工人W建立等待队列Queue，工作质量相同的工人可看作一类工人，该队列中存储正在等待该类工人W的任务。Queue的长度为σ-Eσ，即估计的将要出现的该类工人的数量σ与已经出现的该类工人数量Eσ之差。查看W的等待队列是否超过该类工人出现的个数，若超过，则t的匹配对象自动等待w的近似对象。根据以上规则，可定义损失函数：

(5)

2.6　运行实例

假设目前可以通过阈值算法加入到队列的众包对象有：任务t1、t2和t3、工作地点p1，工人w1和w2,且对所有对象都满足p(t,w)≥θ。其中众包任务的回报值为t1:40，t2:58和t3:100，众包工人的工作质量为w1:0.4和w2:0.96，众包工作地点的容量为3，加入队列的顺序为t3、p1、w1、t1、w2、t2，众包任务回报值的中位数为60，众包工人工作质量的中位数为0.4，且所有的对象都处在其他对象的活动范围内,其分配过程如图4所示。

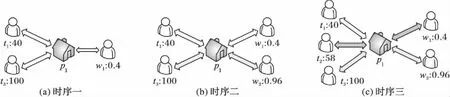
图4　匹配策略运行示意图Fig. 4　Running diagram of matching strategy

如图4所示，当t3、p1、w1出现时，按照匹配策略的规则未进行匹配操作。t2出现后，根据Min-max normalization方法可求得应为t2作出匹配的众包工人的工作质量为0.39，但此时队列中不存在工作质量为0.39的众包工人，由于差异值设为5%,则其近似对象的工作质量取值范围为[0.34,0.44]，故t2与p1、w1进行匹配，得到的效用值为23.2。同理w2出现后与t3匹配，得到效用值为96，总效用为118.2。在不使用匹配策略的情况下，能够进入待分配队列的对象则会按照出现顺序进行分配，得到的效用值为78.4。

3　实验结果与分析

3.1　实验环境

本文实验均使用了处理器为Intel Core i7- 7500U CPU @ 2.70 GHz 2.90 GHz、内存为8 GB(内存频率1 867 MHz)，操作系统为Windows 10的计算机完成。实验使用的编程语言为Python2.7，使用的集成开发环境为PyCharm 2016。实验数据保存在文本文件中，按行读取以表示众包参与者出现的时间和顺序，同时借助了MongoDB存储在文本文件中读取到的实验数据。

3.2　数据集

实验使用gMission的数据集。为了保护隐私，gMission数据集在真实数据集的基础上进行了部分模糊处理。gMission数据集共分为5个数据文件，分别对应将众包活动范围设置为不同数值时所产生的数据，众包活动范围有：10、15、20、25、30。每份数据文件中包含的属性包括众包参与者的类型、出现时间、坐标X、坐标Y、活动范围，这五个属性是共有的。众包任务还有回报值、截止时间两个属性，众包工作地点有容量属性，众包工人有工作质量属性。每个部分的数据集共有6 300条数据，其中包括3 000个任务、3 000个工人、300个工作地点(每个工作地点容量为10)，图5为活动范围为10时的三类对象随时间出现的累计数量。

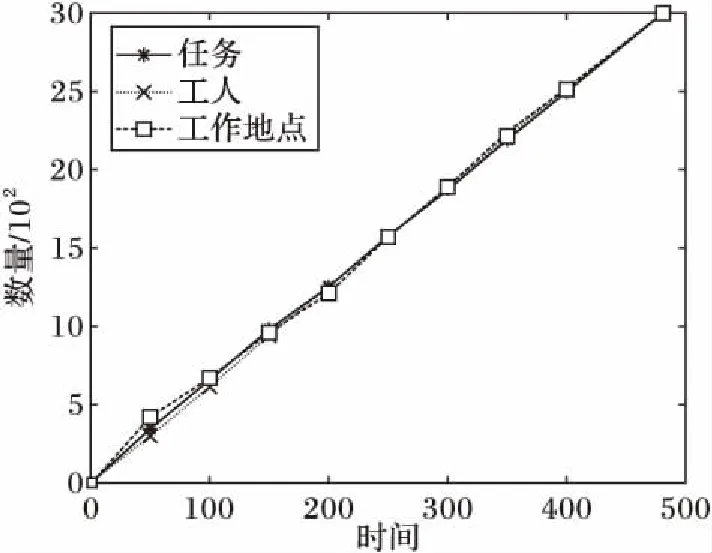
图5　三类对象依时间出现的个数Fig. 5　Numbers of three types of objects which appear in time

3.3　实验设置

本文提出的基于统计预测的自适应阈值算法与贪心算法、随机阈值算法进行对比，评价指标为获得的总效用值，即各个分配得到的效用和。同时本文使用的数据为五种众包活动范围的数据集，观察改变活动范围时效用的变化。在随机阈值算法中，Umax设置为100。在基于统计预测的自适应阈值算法中，初始阈值θ设置为历史数据中任务回报的均值，影响指数β设置为1。

3.4　实验结果

实验结果如图6所示，可以观察到随着活动范围的扩大，总效用也在增长，原因可以归结为随着活动范围的扩大，任务能够在更大的范围内匹配合理的工人。同时，在不同活动范围的数据集上，基于统计预测的自适应阈值算法的总效用始终优于贪心算法和随机阈值算法，并且随着活动范围的不断扩大，贪心算法和随机阈值算法的总效用值趋于不变，而基于统计预测的自适应阈值算法依然可以获得较高的总效用值。

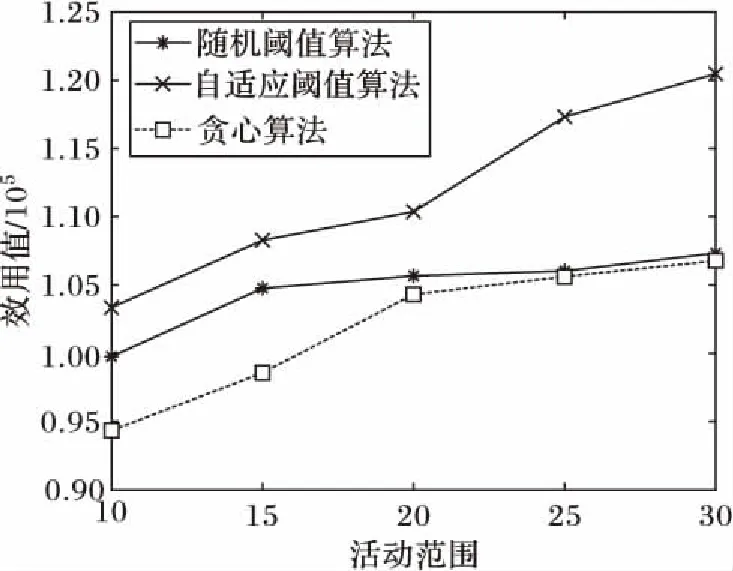
图6　gMission数据集实验结果Fig. 6　Experimental results for gMission data set

3.5　实验分析

通过在真实数据集上进行实验，发现在不同活动范围的条件下，基于统计预测的自适应阈值算法产生的总效用优于贪心算法和随机阈值算法，并且随着活动范围的扩大，总效用的增长不会出现衰减。这说明本文中提出的基于统计预测的自适应阈值算法具有较好的实际应用价值。

4　结语

本文研究了时空众包环境下三类对象的在线分配算法，并分析了贪心算法和随机阈值算法无法获得较高效用的原因，提出了一种基于统计预测的自适应阈值算法。本文在充分理解阈值算法作用机制的前提下，改变了阈值算法的作用对象，提出了旨在最大限度利用可用资源的算法，通过对众包参与者人数的分析，制定阈值的设置及调整策略。通过匹配策略，众包平台的任务分配不再是随机分配，而是一种更具有确定性的分配方式。实验表明，本文提出的任务分配方法能够使众包平台获得更高的总效用值。

参考文献:

[1]CHENG P, JIAN X, CHEN L. Task assignment on spatial crowdsourcing [R/OL]. [2017- 05- 02]. http://arxiv.org/pdf/1605.09675.

[2]KITTUR A, CHI E H, SUH B. Crowdsourcing user studies with Mechanical Turk [C]// CHI ’08: Proceedings of the 2008 SIGCHI Conference on Human Factors in Computing Systems. New York: ACM, 2008: 453-456.

[3]CORMEN T H, LEISERSON C E, RIVEST R, et al. Introduction to Algorithms [M]. Cambridge, MA: MIT Press, 2009: 118.

[4]LEONG HOU U, MAN LUNG YIU, MOURATIDIS K, et al. Capacity constrained assignment in spatial databases [C]// SIGMOD ’08: Proceedings of the 2008 ACM SIGMOD International Conference on Management of Data. New York: ACM, 2008: 15-28.

[5]WONG R C-W, TAO Y, FU A W-C, et al. On efficient spatial matching [C]// VLDB ’07: Proceedings of the 33rd International Conference on Very large Data Bases. New York: ACM, 2007: 579-590.

[6]LONG C, WONG R C-W, YU P S, et al. On optimal worst-case matching [C]// SIGMOD ’13: Proceedings of the 2013 ACM SIGMOD International Conference on Management of Data. New York: ACM, 2013: 845-856.

[7]TONG Y, SHE J, DING B, et al. Online mobile micro-task allocation in spatial crowdsourcing [C]// ICDE 2016: Proceedings of the 2016 IEEE 32nd International Conference on Data Engineering. Piscataway, NJ: IEEE, 2016: 49-60.

[8]LEONG HOU U, MOURATIDIS K, MAMOULIS N. Continuous spatial assignment of moving users [J]. The VLDB Journal — The International Journal on Very Large Data Bases, 2010, 19(2): 141-160.

[9]GAREY M R, JOHNSON D S. Computers and Intractability: A Guide to the Theory of NP-completeness [M]. New York: W. H. Freeman, 1979: 90-91.

[10]MEHTA A. Online matching and ad allocation [J]. Foundations & Trends in Theoretical Computer Science, 2013, 8(4): 265-368.

[11]WANG Y, WONG S C-W. Two-sided online bipartite matching and vertex cover: beating the greedy algorithm [C]// ICALP 2015: Proceedings of the 2015 International Colloquium on Automata, Languages, and Programming, LNCS 9134. Berlin: Springer, 2015: 1070-1081.

[12]TING H F, XIANG X. Near optimal algorithms for online maximum edge-weighted b-matching and two-sided vertex-weighted b-matching [J]. Theoretical Computer Science, 2015, 607(P2): 247-256.

[13]HASSAN U U, CURRY E. A multi-armed bandit approach to online spatial task assignment [C]// UIC-ATC-ScalCom ’14: Proceedings of the 2014 IEEE 11th International Conference on Ubiquitous Intelligence and Computing, and 2014 IEEE 11th International Conference on Autonomic and Trusted Computing, and 2014

IEEE 14th International Conference on Scalable Computing and Communications and Its Associated Workshops. Washington, DC: IEEE Computer Society, 2014: 212-219.

[14]宋天舒，童咏昕.空间众包环境下的三类对象在线任务分配[J].软件学报，2017,28(3):611-630. (SONG T S, TONG Y X. Three types of objects online task allocation space crowdsourcing environment.[J] Journal of Software, 2017, 28(3): 611-630.)

[15]REN J, ZHANG Y, ZHANG K, et al. SACRM: Social Aware Crowdsourcing with Reputation Management in mobile sensing [J]. Computer Communications, 2014, 65: 55-65.

[16]DAI W, WANG Y, JIN Q, et al. An integrated incentive framework for mobile crowdsourced sensing [J]. Tsinghua Science and Technology, 2016, 21(2): 146-156.

[17]张晓航,李国良,冯建华.大数据群体计算中用户主题感知的任务分配[J].计算机研究与发展,2015,52(2):309-317. (ZHANG X H, LI G L, FENG J H. User topic aware task assignment in large data group computing [J]. Journal of Computer Research and Development, 2015, 52 (2): 309-317).

[18]CHEN Z, FU R, ZHAO Z, et al. gMission: a general spatial crowdsourcing platform [J]. Proceedings of the Very Large Data Base Endowment, 2014, 7(13): 1629-1632.