不含双线性对的高效无证书聚合签密方案

苏靖枫，柳菊霞

(1.河南城建学院 计算机与数据科学学院，河南 平顶山467036；　2.洛阳师范学院 信息技术学院，河南 洛阳 471934)(*通信作者电子邮箱33751752@qq.com)

0　引言

签密能够在合理的逻辑步骤内同时实现对消息的签名和加密，与传统的“先签名后加密”的分步密码实现相比，签密机制通信量少、效率高。1997年，Zheng[1]首次提出了签密的概念及具体的签密方案。2002年，Baek等[2]设计出签密方案的安全模型并对Zheng方案的安全性进行了证明。为结合无证书密码体制的优势，2008年，Barbosa等[3]提出一个无证书的签密方案并给出具体的安全模型。随后，多个无证书签密方案相继被提出[4-6]。

聚合签密能组合多个签密密文并进行批量验证，在能耗及实时性要求较高的分布式通信的多对一模式下非常适用，如路由协议、车载网及银行数据处理等。2009年Selvi等[7]提出了一个基于身份的聚合签密方案并证明其安全性，Lu等[8]则提出一个基于双线性对的无证书聚合签密方案(Certificateless Aggregate SignCryption, CLASC)，但这两个方案都不具备可公开验证性，签密及验证签密阶段需要较多的双线性对运算，效率不高。因此，设计安全性能完备且高效的聚合签密方案成为研究热点。如Jiang等[9]、张雪枫等[10]、Eslami等[11]、刘建华等[12]和Yin等[13]提出的CLASC方案。在聚合签密验证阶段，文献[14]的方案需要2n+2个双线性对运算，文献[9，11-13]的方案需要n+3个双线性对运算。分析以上五个CLASC方案，发现它们所使用的双线性对个数均与用户数有关，其高效性只是相对而言的。为进一步减少聚合签密验证阶段的双线性对运算，张玉磊等[14]提出了一个双线性对数为常数、与签密用户数无关的CLASC方案，但在签密阶段仍需要n个双线性对运算。现有的聚合签密方案都是基于耗时的双线性映射构造的，而与指数运算、乘法运算及其他运算相比，双线性对的运算代价要高得多[15]。因此，研究设计不含双线性对的无证书聚合签密方案，能够更好地适用于车载自组织网、无线传感网等资源受限的应用环境

本文基于无证书聚合签密安全模型[11]，提出一种无需双线性对的无证书聚合签密方案。该方案不含复杂的双线性对运算和指数运算，基于计算Diffie-Hellman问题(Computational Diffie-Hellman Problem， CDHP)的困难性构造的部分私钥传输不需要安全信道；同时，聚合签密验证过程不需要任何秘密信息，可以保证方案的可公开验证性。最后，在随机预言模型下证明了该方案满足机密性和不可伪造性。

1　预备知识

1.1　计算困难问题

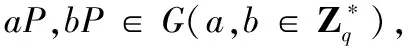
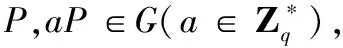
1.2　无证书聚合签密方案形式化定义

本文提出的CLASC方案包含6个算法，分别为系统初始化、用户密钥对生成、签密、聚合签密、聚合签密验证和聚合解签密。

1)系统建立算法：输入一个安全参数k，密钥生成中心(Key Generation Center，KGC)生成系统公开参数params和系统主密钥z，z由KGC秘密保存。

2)用户密钥对生成算法：用户首先选取秘密值xi并计算部分公钥Xi。输入系统参数params、用户身份IDi及Xi，KGC接着输出部分私钥源di及部分公钥Ri。最后，用户验证di的有效性并计算出部分私钥Di。

3)签密算法：输入系统参数params、消息mi、签密者身份IDi、签密者私钥SKi、接收者身份IDB、接收者公钥PKB，输出签密密文σi。

4)聚合签密算法：输入签密者Ui对消息mi的签密密文σi(1≤i≤n)，输出聚合签密密文δ。

5)聚合签密验证算法：输入系统参数params、签密用户的身份-公钥对(IDi,PKi)(1≤i≤n)，接收者验证聚合密文δ的合法性。如果验证通过，则输出true，否则输出false。

6)聚合解签密算法：如果“聚合签密验证算法”输出为true，则执行该算法。输入聚合密文δ、接收者身份IDB及其私钥SKB。输出消息mi(1≤i≤n)。

1.3　无证书聚合签密方案安全模型

参照文献[11]所定义的安全模型，CLASC方案需考虑两种类型的敌手：AⅠ和AⅡ。AⅠ属于一般用户，可以查询和替换合法用户的公钥，实施公钥替换攻击；AⅡ代表恶意的KGC，能够获取系统主密钥和用户的部分私钥，实施伪造攻击。因此，CLASC方案的安全性需分别考虑两类敌手攻击下的保密性和不可伪造性，具体定义如下。

定义1如果CLASC方案能够抵抗敌手AⅠ和AⅡ的适应性选择密文攻击，则方案在适应性选择密文攻击下具有不可区分的安全属性[11]。

定义2如果CLASC方案能够抵抗敌手AⅠ和AⅡ的适应性选择消息攻击，则方案在适应性选择消息攻击下具有存在不可伪造性[11]。

2　不含双线性对的无证书聚合签密方案

在车载自组织网应用场景中，当城市交通拥堵时，1个路边单元(Road Side Unit, RSU)通常需要管辖上百辆车辆，可以利用聚合签密技术，在短时间内对来自大量的车载基础单元(On-Board Unit, OBU)的签密信息进行批量验证。本文提出一个不含双线性对的无证书聚合签密方案，结合车载自组织网应用场景来详细描述本文方案的实现过程。方案的合法参与者有服务中心(Service Center， SC)、车载基础单元OBUi(1≤i≤n)、聚合签密器Agg-tor和路边单元RSU，密钥生成阶段集成了密钥的选择及部分私钥的提取。具体实现过程如下：

1)系统参数建立。

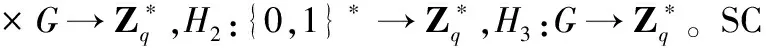
2)密钥生成。

此过程包括私钥生成及部分私钥提取，步骤如下：

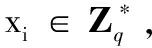
c)为确保(Ri,di)的有效性，OBUi首先验证等式Ri+PpubH1(IDi,Ri,Xi)+PH3(xiPpub)=diP是否成立，若成立，接着计算其部分私钥Di=di-H3(xiPpub)(若需要，SC也可以计算出OBUi的部分私钥Di=ri+zH1(IDi,Ri,Xi))。这样，OBUi的私钥为SKi=(Di,xi)，公钥为PKi=(Ri,Xi)。

同样,路边单元RSU的私钥为SKB=(DB,xB)，公钥为PKB=(RB,XB)

3)签密。

假定参与签密的车载基础单元OBUi的身份信息为IDi，聚合签密接收者RUS的身份和公钥分别为IDB和PKB，待签密的消息为mi(1≤i≤n)。具体步骤如下：

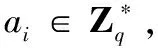
4)聚合签密。

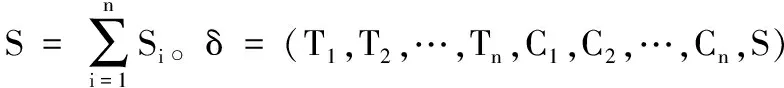
5)验证聚合签密。

给定n个OBUi的身份-公钥对(IDi,PKi)及系统公开参数，RUS验证δ=(T1,T2,…,Tn,C1,C2,…,Cn,S)的合法性，步骤如下：

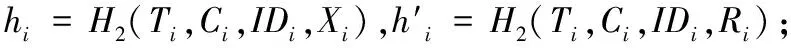
b)验证下面等式是否成立:

如果等式成立，证明聚合签密是有效的，否则拒绝接受。

6)解聚合签密。

如果聚合签密验证通过，RSU则利用自己的私钥SKB解密出消息，其中1≤i≤n。执行步骤如下：

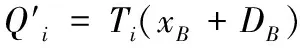
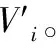
3　方案的安全性分析

3.1　正确性

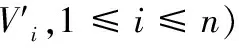
a)聚合签密的合法性验证。

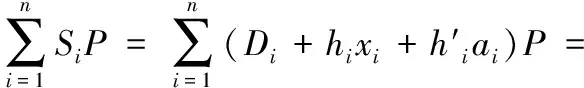
b)解密密文的正确性检查。

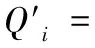
ai(XB+RB+PpubH1(IDB,RB,XB))=Qi

3.2　不可伪造性

定理1随机预言模型下，基于DLP，本文提出的CLASC方案在适应性选择消息攻击下是存在性不可伪造的(EUF-CLASC-CMA)。

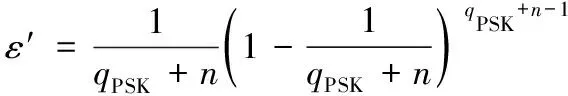
证明挑战者Ç给定一个随机的DLP实例(P,aP)，Ç的目的是通过与敌手AⅠ的交互求解DLP，即求出a。

1)系统初始化阶段。

Ç设Ppub=aP(这里a默认作为系统主密钥，并且对AⅠ保密)，选择并发送系统参数params=(p,q,P,Ppub,H1,H2,H3)给敌手AⅠ。

2)问询阶段。

AⅠ适应性地执行以下预言机问询，Ç维护以下6个列表L1、L2、L3、Ls、Lsk、Lpk分别用于记录AⅠ对预言机H1、H2、H3、秘密值提取、部分私钥提取、公钥提取的问询数据，列表初始化均为空。

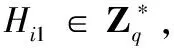
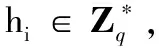
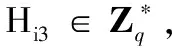
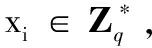
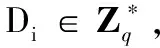
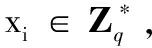
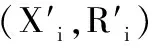
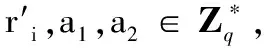
3)伪造阶段。

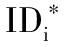
即

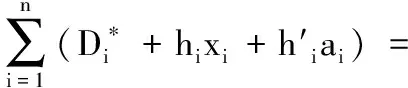
E1：Ç在模拟过程中没有终止的情况；

E2：伪造的聚合签密δ*是有效且非平凡的；

E3：在E2发生的前提下，不失一般性，满足c1=1，ci=0(2≤i≤n)。

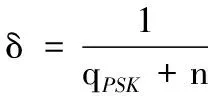
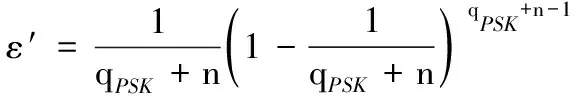
证明挑战者Ç给定一个随机的DLP实例(P,aP)，Ç的目的是通过与敌手AⅡ的交互求解DLP，即求出a。敌手AⅡ在这里充当恶意的SC，除掌握引理1中的给定的条件外，还拥有系统主密钥z。AⅡ能够执行除引理1中的“公钥替换问询”和“部分私钥提取问询”以外的所有询问。除“公钥提取问询”和“签密问询”外，其他同引理1。

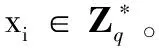
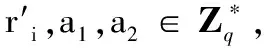
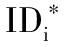
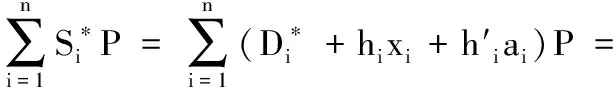
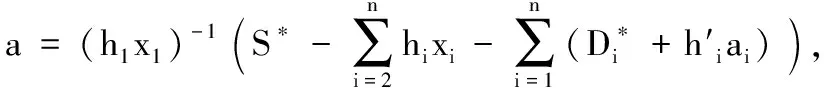
3.3　机密性

定理2随机预言模型下，基于CDHP，本文提出的CLASC方案在适应性选择密文攻击下是不可区分的(IND-CLASC-CCA2)。

引理3随机预言模型下，如果存在概率多项式时间敌手AⅠ(或AⅡ)以不可忽略的概率赢得游戏，则存在挑战者Ç能够以不可忽略的概率解决CDHP的一个实例。

引理3的证明方法与Eslami方案[11]的保密性证明方法类似，限于篇幅，此次不再给出具体过程。

4　方案性能及效率分析

4.1　性能分析

4.1.1部分私钥生成不需要安全信道

在本文方案中，服务中心SC首先计算出车载基础单元OBUi的部分私钥对应的部分私钥源di=ri+zH1(IDi,Ri,Xi)+H3(zXi)，然后通过公开信道发送di给OBUi，最后OBUi通过计算Di=di-H3(xiPpub)得到自己的部分私钥Di。若有需要，SC也可以通过计算Di=ri+zH1(IDi,Ri,Xi)得到OBUi的部分私钥。若部分私钥源di在经公开信道传递时被攻击者监听到，攻击者将会尝试借助两种方法得到部分私钥：其一，计算Di=di-H3(xiPpub)，由于得不到OBUi的秘密值xi，所以计算不出Di；其二，计算Di=ri+zH1(IDi,Ri,Xi)，也会由于无法得到系统主密钥而失败。所以，本文方案的部分密钥的分发不需要安全信道。

4.1.2可公开验证性

当签密发送者车载基础单元OBUi和签密接收者路边单元RSU关于聚合签密密文的真伪发生争执时，任意第三方均可验证下面等式：

因为该等式的验证无需接收者的参与，且不需要任何用户的秘密信息，因此方案具有可公开验证性。

4.2　效率分析

表1对本文方案和已有的典型方案的效率进行了比较。假设参与签密的用户有n个，这里考虑三种运算：指数运算(标识为E)、群G上的乘法运算(标识为S)、双线性对运算(标识为P)。相比较前三种运算，散列函数运算和异或运算的耗时对整体效率的影响可以忽略不计。为分析方案的通信开销，表2对本文方案和已有的典型方案的密文长度进行了比较。其中，|G1|和|G|为相应群中元素的长度，|m|和|U|分别表示消息和用户身份的长度。

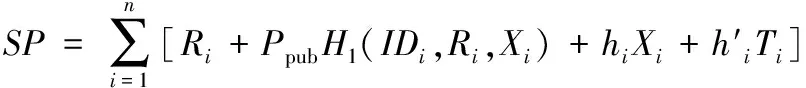
表1　计算效率与密文长度比较Tab. 1　Comparison of computational efficiency and ciphertext size

5　结语

无证书聚合签密利用了无证书密码体制的优势，能够对签密的信息进行聚合传输和批量验证，大大降低了计算复杂度和通信代价。本文设计了一个无需双线性对的无证书聚合签密方案，对比已有的方案，本文方案有效地提高了计算效率且密文长度更短。同时，在随机预言模型下，基于CDHP和DLP证明了方案满足不可伪造性和机密性，并且部分私钥的传输不需要安全信道。因此，本文方案适用于计算资源和带宽受限的聚合签密应用环境。

参考文献:

[1]ZHENG Y. Digital signcryption or how to achieve cost(signature & encryption)<

[2]BAEK J, STEINFELD R, ZHENG Y L. Formal proofs for the security of signcryption [C]// PKC 2002: Proceedings of the 2002 International Workshop on Public Key Cryptography, LNCS 2274. Berlin: Springer, 2002: 80-98.

[3]BARBOSE M, FARSHIM P. Certificateless signcryption [C]// ASIACCS ’08: Proceedings of the 2008 ACM Symposium on Information, Computer and Communications Security. New York: ACM, 2008: 369-372.

[4]ZHOU C, ZHOU W, DONG X. Provable certificateless generalized signcryption scheme [J]. Designs, Codes and Cryptography, 2014, 71(2): 331-346.

[5]SHI W, KUMAR N, GONG P, et al. Cryptanalysis and improvement of a certificateless signcryption scheme without bilinear pairing [J]. Frontiers of Computer Science, 2014, 8(4): 656-666.

[6]夏昂,张龙军.一种新的无双线性对的无证书安全签密方案[J].计算机应用研究,2014,31(2):532-535. (XIA A, ZHANG L J. New secure certificateless signcryption scheme without pairing [J]. Application Research of Computers, 2014, 31(2): 532-535.)

[7]SELVI S S D, VIVEK S S, SHRIRAM J, et al. Identity based aggregate signcryption schemes [C]// INDOCRYPT 2009: Proceedings of the 10th International Conference on Progress in Cryptology, LNCS 5922. Berlin: Springer, 2009: 378-397.

[8]LU H J, XIE Q. An efficient certificateless aggregate signcryption scheme from pairings [C]// ICECC 2011: Proceedings of the 2011 International Conference on the Electronics, Communications and Control. Piscataway, NJ: IEEE, 2011:132-135.

[9]JIANG Y, LI J, XIONG A. Certificateless aggregate signcryption scheme for wireless sensor network [J]. International Journal of Advancements in Computing Technology, 2013, 5(8): 456-463.

[10]张雪枫,魏立线,王绪安.无证书的可公开验证聚合签密方案[J].计算机应用,2013,33(7):1858-1860. (ZHANG X F, WEI L X, WANG X Z. Certificateless aggregate signcryption scheme with public verifiability[J]. Journal of Computer Applications, 2013, 33(7): 1858-1860.)

[11]ESLAMI Z, PAKNIAT N. Certificateless aggregate signcryption: security model and a concrete construction secure in the random oracle model [J]. Journal of King Saud University Computer and Information Sciences, 2014, 26(3): 276-286.

[12]刘建华,毛可飞,胡俊伟.基于双线性对的无证书聚合签密方案[J].计算机应用,2016,36(6):1558-1562. (LIU J H, MAO K F, HU J W. Certificateless aggregate signcryption scheme based on bilinear pairings [J]. Journal of Computer Applications, 2016, 36(6): 1558-1562.)

[13]YIN S-L, LI H, LIU J. A new provable secure certificateless aggregate signcryption scheme [J]. Journal of Information Hiding and Multimedia Signal Processing, 2016, 7(6): 1274-1281.

[14]张玉磊,王欢,李臣意,等.可证安全的紧致无证书聚合签密方案[J].电子信息学报,2015,37(12):2838-2844. (ZHANG Y L, WANG H, LI C Y, et al. Provable secure and compact certificateless aggregate signcryption scheme [J]. Journal of Electronics and Information Technology, 2015, 37(12): 2838-2844.)

[15]DENG L, ZENG J, QU Y. Certificateless proxy signature from RSA [J]. Mathematical Problems in Engineering, 2014, 2014(9): Article ID 373690.

[16]张华,温巧燕,金正平.可证明安全算法与协议[M].北京:科学出版社,2012:76-77. (ZHANG H, WEN Q Y, JIN Z P. Provable Security Algorithms and Protocols [M]. Beijing: Science Press, 2012: 76-77.)