农机复杂件精密模型数控加工和成型技术研究
张铁创,徐文静
(洛阳职业技术学院,河南 洛阳 471003)
0 引言
复杂零件造型技术是计算机辅助设计和计算机图形学中最为活跃、最为关键的学科分支之一[1-3]。随着现代制造技术的发展和CAD/CAM软件功能的日趋完善,采用数控编程技术已成为复杂零件精密加工的主要方法[4-6]。农用果园修理机的驱动装置部分由于叶轮的存在,曲面形状较多,其零部件的加工较为困难[7-13]。如果采用造型技术,利用NURBS插补算法,先对加工刀具的轨迹进行规划,通过仿真技术确定刀具参数后再实际加工,会大大零件的加工效率,对于复杂农机零件的设计和制造工艺的制定都具有重要的意义[13-19]。
1 复杂零部件数控加工技术
对于复杂曲面类零件,由于其曲面不能采用直接编程加工的方法,所以加工精度较低[19-24]。近年来,随着数控编程技术和先进制造机床的高速发展,具有复杂编程功能的多轴加工机床可以满足复杂件的加工需要。例如,山西机电职业技术学院宋理敏等采用数据加工的方法,对椭圆类复杂零件进行了工艺分析,通过数据加工最终得到了加工产品,如图1所示[25-27]。

图1 椭圆类复杂零件加工产品
采用曲线插补技术可以完成椭圆类等复杂曲面的零件的加工,保持零部件和装配体等。本研究基于NURBS曲线插补技术,其加工流程如图2所示。采用NURBS曲线插补的数控加工系统的工艺路线主要包括图纸分析、自动数控编程、刀具轨迹生成、程序输出和实际数控加工,而NURBS曲线插补主要是采用数学建模的形式。
2 基于NURBS曲线的刀具轨迹插补算法
果树修理机驱动装置由椭球面类叶轮轴和叶片、轴套、凸轮轴、底座及台阶销等多个零件构成,以椭球面类叶轮轴和叶片最为复杂,如图3所示。
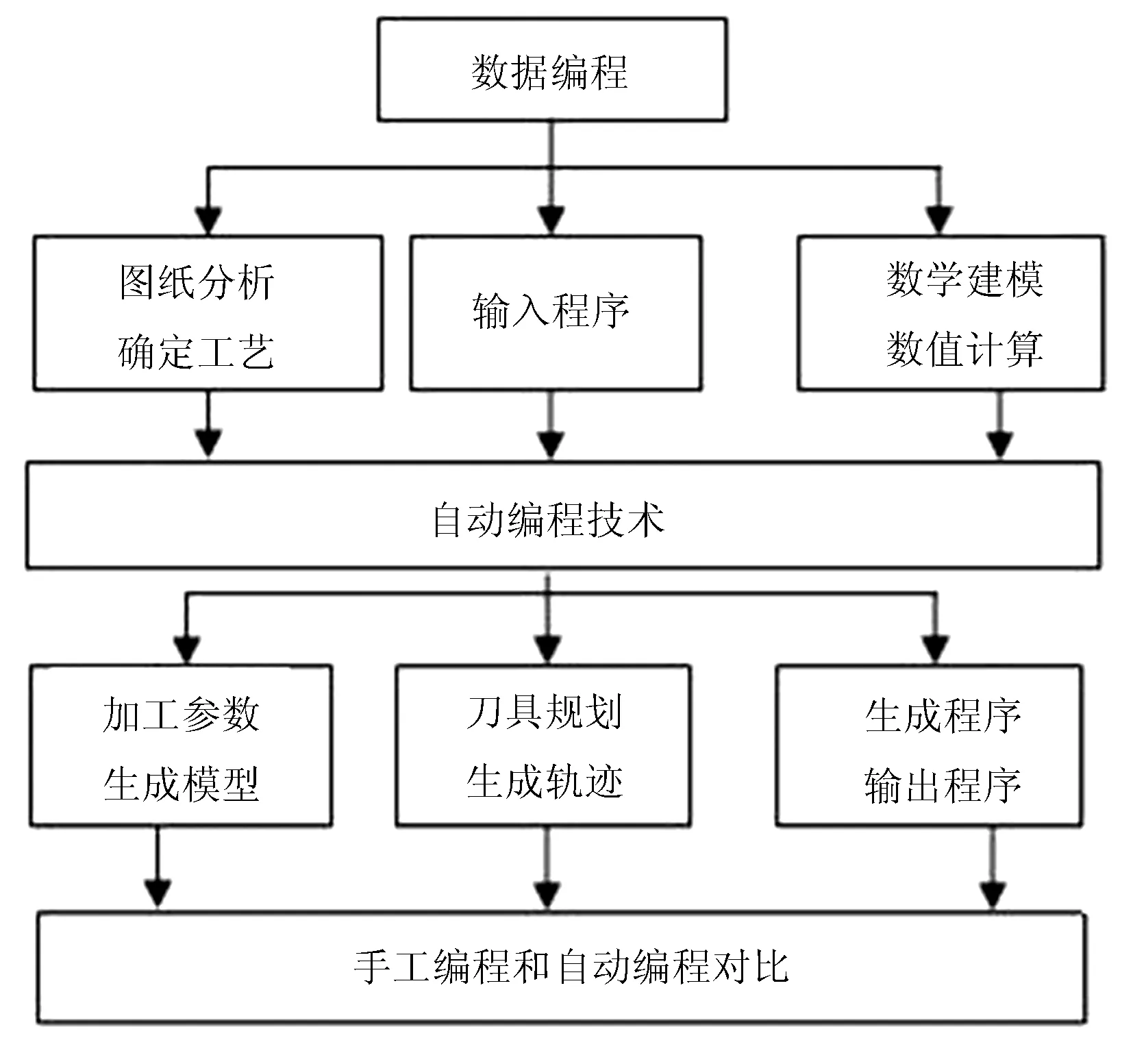
图2 基于NURBS曲线插补的数控加工流程

图3 农机椭球面类叶轮轴和叶片复杂零部件
叶轮部分属于复杂的机械零部件,由于存在较多的曲面,采用一般的方法很难进行加工,而借助曲线插补技术可以实现这种复杂零件的精密加工。NURBS曲线通常被称作非均匀有理B样条曲线,主要由3部分组成,其表达式可以写成
(1)
其中,P(K)为NURBS上的位置向量;Ni,m(K)为m次样条基函数;Pi为曲线的控制点;Ri为权因子;K为节点向量。由递推公式可得
(2)
在农机复杂零部件数控加工时,曲面部分可以采用曲线插补的形式,具体需要借助于NURBS曲线插值。假设给定n+1个型值点,从而可以构造一条k次的NURBS曲线,曲线的端点是首和末的型值点。将曲线按照型值点进行分段,分为n段后有n+k个控制顶点di(i=0,1,....,n+k-1)。节点矢量U=[u0,u1,...,un+2k],u0=u1...=uk≤uk+1=un+k+1=...=un+2k,在数控编程时可以采用三次NURBS曲线拟合。三次曲线具有个控制点和个节点矢量,具体可以表示为
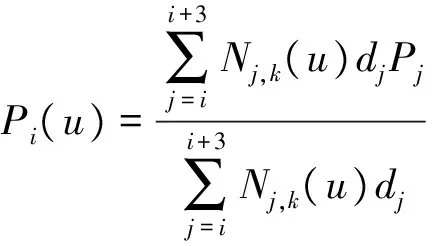
(3)
令t=(u-ui+3)/(ui+4-ui+3),则三次NURBS曲线可以表示为矩阵形式,即

(4)
其中
(5)
根据NURBS曲线的插值原理,可以采用曲线插补的方法对农机复杂零部件加工进行数控编程,其流程如图4所示。
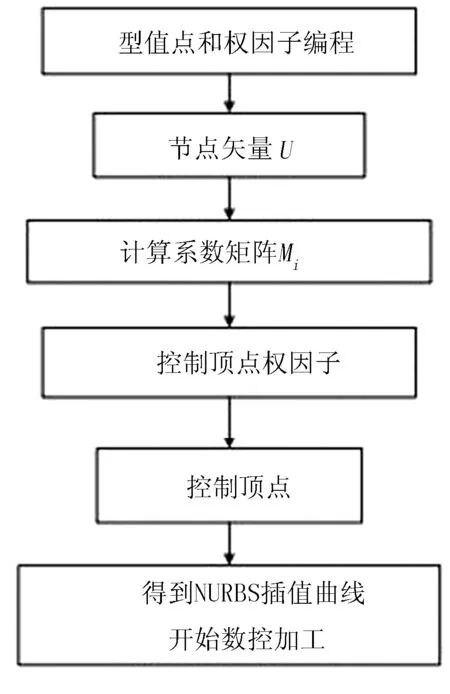
图4 NURBS曲线插补算法编程流程
采用曲线插补算法进行数控编程时,首先需要设置型值点和权因子的数据;然后,计算节点矢量U和系数矩阵Mi,得到控制顶点的权因子后求出控制顶点;最终得到NURBS插值曲线作为数控加工的刀具轨迹线。
3 农机复杂精密件数控加工测试
为了验证NURBS曲线插补技术在数控加工刀具轨迹控制中使用的可行性,采用五轴数控加工铣床进行了实验测试。实验采用数控编程的方法,农机的机型如图5所示。

图5 果树修剪农机
图5为一款果树修理农机,其驱动装置采用了较为复杂的机械零部件。由于曲面较多,在加工制造时需要采用曲线插补技术,具有曲线插补功能的数控系统示意图如图6所示。
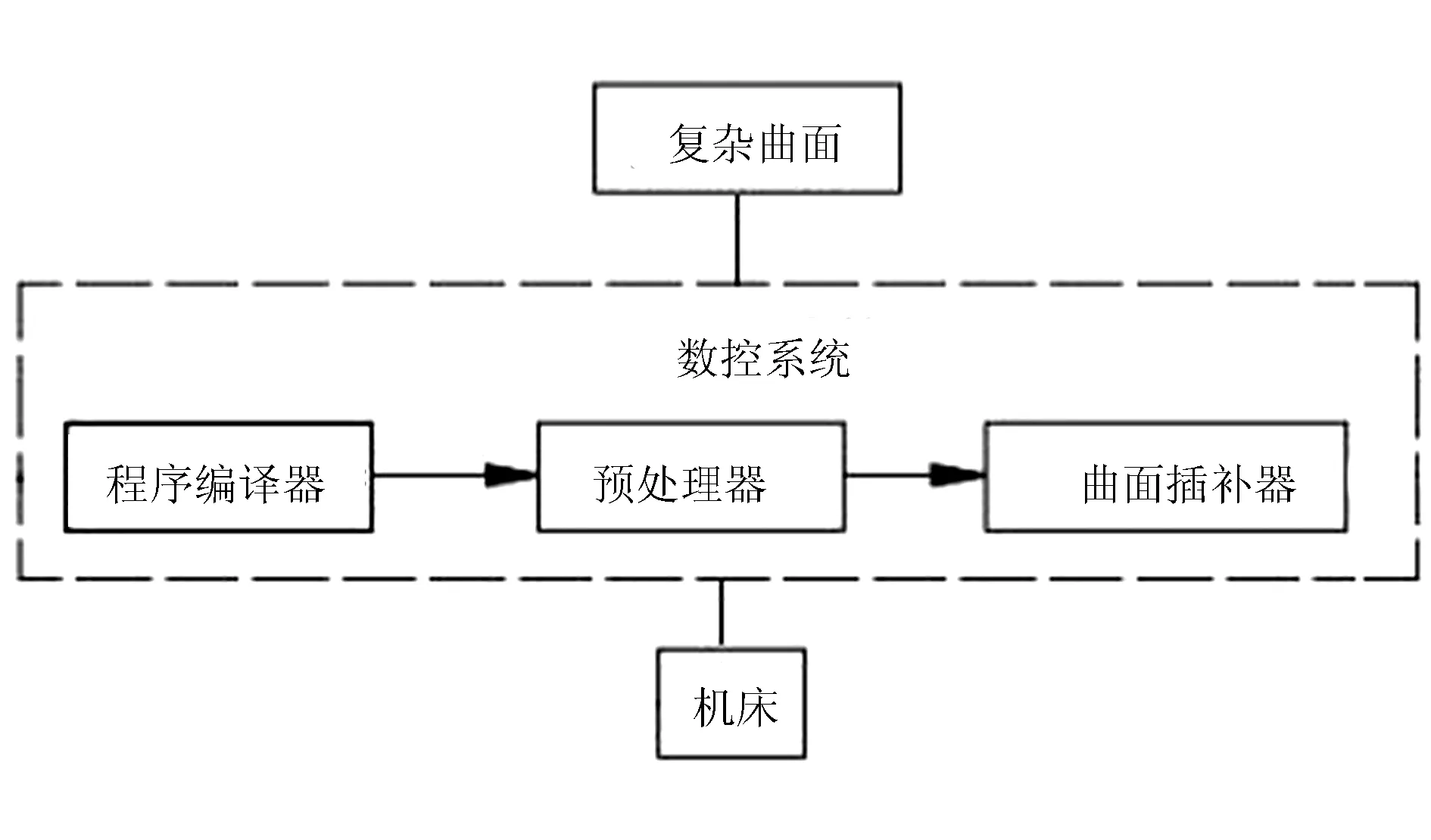
图6 NURBS曲面插补数控系统
在数控系统中引入曲线插补功能后,CNC系统刀具轨迹可以由简单的直线运动变为曲线运动,可以对曲面进行加工,从根本上解决了传统的系统做不到的功能。
铣削加工中常用的刀具有带倒圆的端铣刀、球头铣刀及平面端铣刀等,本次数控加工采用的是球面铣刀,在加工复杂曲面时具有更好的光滑性。利用软件编程对NRUBS曲线插补轨迹进行规划后,得到了如图8所示的效果图。
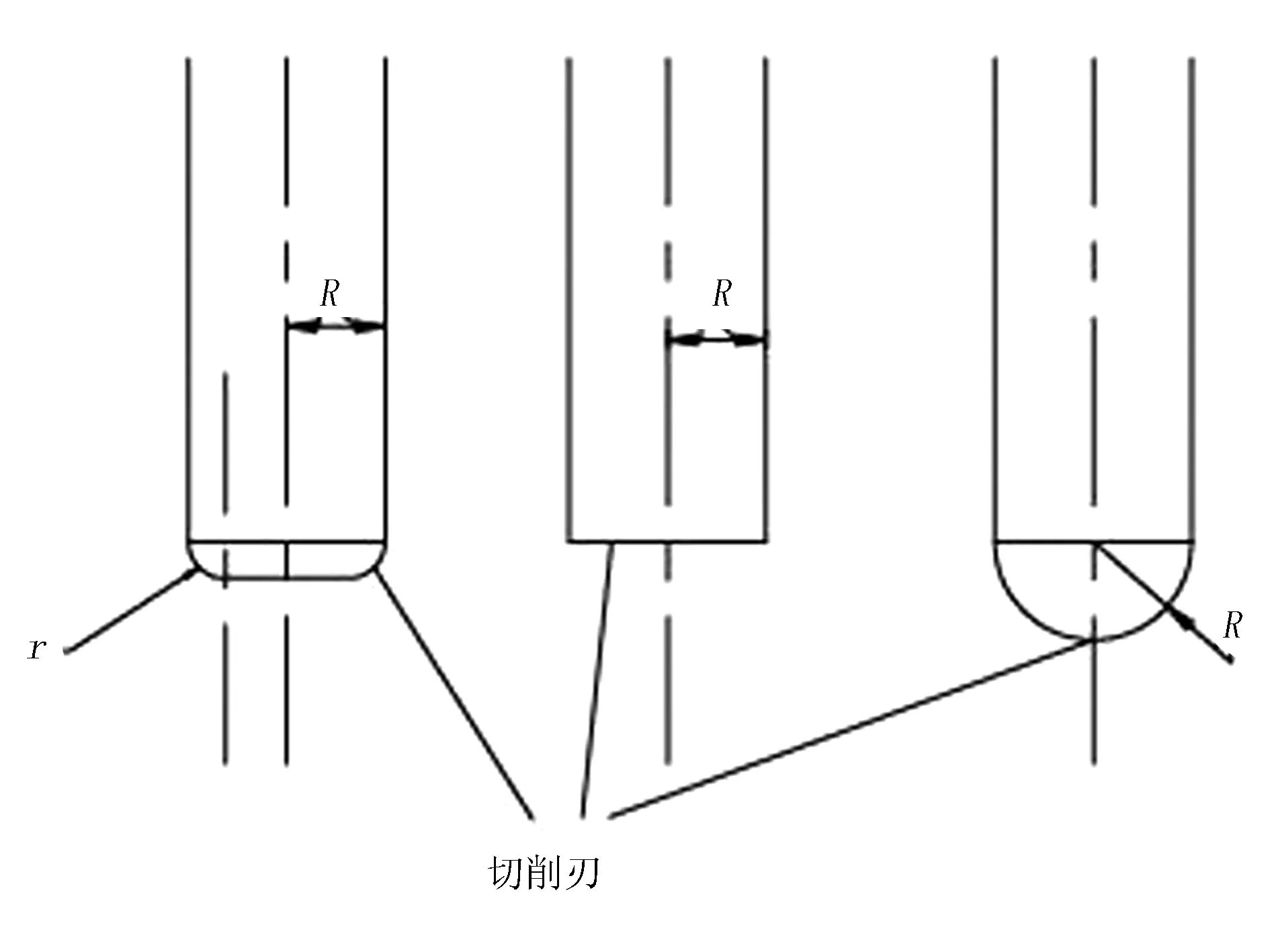
图7 刀具库示意图
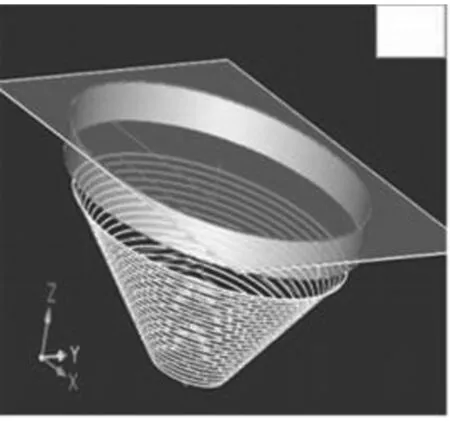
图8 刀具轨迹规划图
采用NURBS曲线插补算法可以成功地实现曲面的刀具规划,在数控加工时采用该形状的走刀轨迹,可以实现复杂曲面的加工,其加工效果如图9所示。

图9 NURBS插补和传统加工方法对比
为了验证基于NURBS插补算法的可靠性,将采用该种曲线插补算法加工的零件(a)和传统的加工方法加工的零件(b)进行了对比,如图9所示。
对同一个数控加工轨迹点进行了跟踪测试,得到了仿真轨迹和实际加工的对比曲线,结果表明:实际加工曲线和仿真曲线非常吻合,从而验证了NURBS插补算法的可靠性。

图10 仿真和实际加工曲线对比
4 结论
在果园修剪机的复杂零部件加工制造时,由于存在较为复杂的曲面部分,给数控加工过程带来了较大的困难。为了解决这个问题,将基于NURBS曲线插补算法引入到了数控编程过程中,并根据预先设计好的数学模型,生成了刀具的走刀轨迹。为了验证方法的可行性,采用虚拟仿真的形式对刀具的轨迹进行了实验,通过优化确定了刀具的具体参数数据。根据插补算法制定的走刀轨迹,对零件进行了实际加工,将加工的零件和传统方法加工的零件进了对比,充分验证了基于NURBS曲线插补算法加工的优越性。
参考文献:
[1]梅伶.浅析曲面回转体零件的数控车削加工[J].机床液压,2007,35(8):76-78.
[2]陈汇,郎利辉,杜传军,等.薄壁精密罐多次缩口过程及其机理[J].北京航空航天大学学报,2011,37(7): 805-810.
[3]刘宏,罗丽丽,樊永强.三轴椭球精密曲面的数控双指令铣削加工技术[J].制造业自动化,2015,37(10):21-23.
[4]丁汉,毕庆贞,朱利民,等.五轴数控加工的刀具路径规划与动力学仿真[J].科学通报,2010(25):2510-2519.
[5]王晶,张定华,罗明,等.复杂曲面零件五轴加工刀轴整体优化方法[J].航空学报,2013(6):1452-1462.
[6]罗明,吴宝海,李山,等.自由曲面五轴加工刀轴矢量的运动学优化方法[J].机械工程学报,2009(9):158-163.
[7]章永年,赵东标,陆永华,等.平底刀最优刀轴矢量规划算法[J].机械工程学报,2012(5):180-186.
[8]姬俊锋,周来水,安鲁陵,等.一类开式整体叶轮五坐标数控加工刀轴矢量生成及其光顺方法的研究[J].中国机械工程,2009(2):202-206.
[9]任军学,何卿功,姚倡锋,等.闭式整体叶盘通道五坐标分行定轴加工刀轴矢量规划方法[J].航空学报,2012(10):1923-1930.
[10]李炳林,王学林,胡于进,等.基于区域划分的刀具方向控制方法[J].中国机械工程,2010(4):452-457.
[11]陈晓兵,廖文和,戴宁.三角网格曲面等参数线刀轨生成算法[J].中国机械工程,2013(8):1047-1051.
[12]乐英,韩庆瑶,贾军.复杂曲面数控加工刀具轨迹的生成技术[J].机床与液压,2008(6):25-27.
[13]孙玉文,刘伟军,王越超.基于三角网格曲面模型的刀位轨迹计算方法[J].机械工程学报,2002(10):50-53.
[14]上官文斌,王益有,吴敏,等.基于无量纲性能曲线的发动机冷却风扇设计方法[J].汽车工程,2010,32(5): 455-458.
[15]席光,王志恒,王尚锦.叶轮机械气动优化设计中的近似模型方法及其应用[J].西安交通大学学报,2007, 41(2):125-135.
[16]赵其国.当前我国农业发展中存在的深层次问题及对策[J].生态环境学报,2013,22(6):911-915.
[17]赵其国,黄国勤,王礼献.中国生态安全、农业安全及“三农”建设研究[J].农林经济管理学报,2014,13(3):237-243.
[18]高春城.我国农业发展的资源环境问题与展望[J].当代生态农业,2013,3(4):151-154.
[19]万宝瑞.当前我国农业发展的趋势与建议[J].农业经济问题,2014,4(1):110-114.
[20]徐茂,邓蓉.国内外设施农业发展比较[J].北京农学院学报,2014,29(2):75-79.
[21]孙殿柱,康新才,孙永伟,等.基于三角Bézier曲面刀轨快速生成算法[J].北京工业大学学报,2012(10): 1446-1450.
[22]刘雄伟,张平,刘飞鹏,等.基于三角面-三角形相交检测的五轴数控加工碰撞干涉检测算法研究[J].机床与液压,2011(9):23-26.
[23]张永超,于洋.五坐标加工中使用坐标内插法控制刀具轴向研究[J].组合机床与自动化加工技术,2011(8): 39-42.
[24]王秋红,葛胜兰,陈德华.利用FANUC宏程序铣削半球零件的3种方法[J].机床与液压,2011,39(16):81- 84.
[25]赵晓燕,刘志刚.宏变量在数控加工中的应用[J].现代制造工程,2010(8):121-122.
[26]王锋波,孙士彬.FANUC系统宏程序在抛物线类零件中的应用[J].煤矿机械,2011(10):148-150.
[27]牛卫中.薄壁圆筒工件抛物面性缩口成形的力学分析[J].金属成形工艺,2003,21(3):43-45.
ID:1003-188X(2018)04-0037-EA

