基于GA-LM-BP模型的云南省农机总动力预测
胡陈君,陈 建,王 卓,王 攀,曹中华,郑延莉,王炎林,牛 坡
(西南大学 工程技术学院,重庆 400715)
0 引言
农机总动力是指用于农、林、牧、渔业生产和运输的所有机械动力的总和,它反映一个地区农机装备的总体水平,是农机化发展规划的主要指标[1]。农机总动力数量变化是非线性的,BP神经网络作为一种具有较强非线性模拟能力与较高精度、较强自学习与自适应能力的学习算法,能对其进行分析;但传统的BP神经网络采用误差梯度下降法调节权值,存在网络收敛速度较慢、全局搜索能力弱及易陷入局部极小等缺点。LM算法是梯度下降法与高斯-牛顿法的结合,具有高斯-牛顿法的局部收敛性和梯度下降法的全局特性,在局部搜索能力上强于BP神经网络,且其收敛速度很快且精度也高,解决了BP网络的“局部收敛”问题;但LM算法对网络的初始权值与阈值过于依赖,存在对初始权阈值敏感、泛化能力不强的缺点。遗传算法(GA)具有较强的全局搜索能力,且简单通用、鲁棒性强,通过优化BP神经网络的连接权,能较好地克服BP神经网络盲目选择连接权值的缺点,但其训练时间较长,局部搜索能力较弱。将LM算法与GA算法结合,运用GA算法优化BP神经的初始权值与阈值,可以提高网络的泛化能力;采用LM算法训练BP神经网络,可提高网络收敛速度,避免网络训练陷入局部极小点,克服了LM算法与GA算法单一结合BP神经网络的缺点[2-4]。因此,本文利用1985-2015年云南省农机总动力数据,建立GA-LM-BP神经网络预测模型对云南省农机总动力进行预测。
1 GA-LM-BP模型
1.1BP神经网络
BP (Back Propagation)神经网络是一种单向传播的多层前馈神经网络,是目前应用最广泛的神经网络,主要特点是信号前向传播及误差反向传播。该算法的精髓是将网络的输出与期望输出间的误差通过反向传播“分摊”到各神经元的权值和阈值,通过多次迭代使BP 神经网络预测输出不断逼近期望输出。BP神经网络的结构比较简单,由输入层、隐含层和输出层组成,每层包含若干神经元,不同层神经元间通过权值形成全互连连接,同层神经元间无连接,且理论上已证明隐含层为一层的神经网络结构,可以模拟任意复杂的非线性映射关系[5]。
1.2LM算法
LM(Levenberg-Marquardt)算法是梯度下降法与高斯-牛顿法相结合的一种数值优化快速算法,同时具有梯度下降法和高斯-牛顿法的优点。其基本思想是允许误差沿着恶化的方向搜索,使网络每次不再沿着单一的负梯度方向迭代,同时对网络的权值进行自适应调整优化,提高了网络的收敛速度,同时最大限度地解决了BP神经网络陷于局部极小点的问题[6]。
1.3GA算法
遗传(GA)算法是一种基于自然选择和基因遗传学原理的优化搜索方法,具有很强的宏观搜索能力与良好的全局优化能力。其基本思想是:随机对初始化的种群基因编码,通过适应度函数检验个体的好坏,然后经遗传操作(选择、交叉、变异)产生新的个体,且反复迭代收敛得到最优个体经过解码作为问题的最优解或近似最优解[7]。
1.4GA-LM-BP模型
GA-LM-BP模型是将GA算法与LM算法结合优化BP神经网络,改善了LM算法优化BP神经网络的收敛性,强化了GA算法的进化能力。其基本思想是:由GA算法优化确定BP神经网络的初始权值与阈值,确定一个较好的搜索空间,代替一般初始权值与阈值的随机选取;然后应用LM算法在这个解空间里对网络进行训练、学习至收敛,搜索出最优解或者近似最优解。其主要步骤如下:
1)输入BP神经网络的训练样本集X= [x1,x2,…,xn]T,确定BP神经网络的结构为n-l-m(n、l、m分别为输入层、隐含层和输出层节点个数),初始化BP神经网络的阈值向量θ,产生初始随机训练权值w,并给出误差允许值ε,且令常数k= 0,μ=μ0。
2)计算BP神经网络的输出L与误差目标函数E(X)。根据输入样本X,连接权值w与阈值θ可得
其中,fl、fm为隐含层与输出层的传递函数;a为输入层节点且a∈[1,n];b为隐含层节点且b∈[1,l];c为输出层节点且c∈[1,m]。网络输出与期望输出之间的差别就是BP神经网络的误差,定义该误差目标函数E(X)为
3)权值向量的调整,其计算公式为:wk+1=wk+Δw。其中,Δw为BP神经网络训练过程中权值的调整量,BP神经网络训练过程中由LM算法优化,则
Δw=-(JT(X)·J(X)+μ·I)-1JT(X)·e(X)
e(X)=[e1(X),e2(X),…eN(X)]T
其中,μ为一个非负值;I为单位矩阵;J(X)为误差对权值微分的雅克比矩阵。
4)判断E(X)。若其小于ε,则训练结束;否则进入下一步,即计算误差指标函数E(Xk+1)。若E(Xk+1) 5)种群初始化及种群规模与进化代数的设定。本文采用简单、易实现的实数编码实现种群初始化,种群规模为群体中所含个体数目,每个个体表示为染色体的基因编码,且数目一定。 6)判断进化代数是否满足设定值,若满足则转至步骤2),GA算法结束;否则进入下一步,即个体适应度值的计算。本文将BP神经网络的预测输出值yi与真实值oi之间的绝对误差值和的倒数作为个体适应度值,计算公式为 本文利用该适应度函数计算每个个体的适应度值,判断其适应度值是否符合优化准则。若符合,则转到步骤2);否则,进入下一步。 7)根据适应度对个体进行遗传(选择、交叉、变异)操作,得到新一代的种群,然后返回步骤6)。选择操作采用轮盘赌法,使适应度值高的个体有更大的概率被选择到下一代。选择概率为 交叉操作因个体采用实数编码而采用实数交叉法,第k个染色体和第l个染色体在j位的交叉,则 akj=akj(1-b)+aljb alj=alj(1-b)+akjb 其中,b为0~1间随机数。 变异操作选取第i个个体的第j个aij基因进行变异,则 其中,amax为基因aij的上界;amin为下界;f(g) =r2(1-g/Gmax)2;r2是随机数;g为当代迭代次数;Gmax为最大进化次数;r为0~1间随机数。 2.1样本数据的获取及处理 本文根据中国统计年鉴选取了1985-2015年间云南省农机总动力的历史统计数据作为训练样本[8],但农机总动力数据值较大,作为神经网络的训练值将使得神经网络结构复杂且不易收敛,因而该数据需先进行归一化处理。归一化方法为 式中Xi—输入样本数据; Xmax、Xmin—输入样本数据的最大值与最小值; Xi—归一化后的样本输入数据,Xi’∈[a,b]。 逆变换公式为 BP神经网络的激活多采用Sigmoid函数,其输出值在0~1或-1~1之间;但该函数值接近0或1时,曲线比较平缓,变化速度非常缓慢。为了减小BP网络学习时间,加大函数在区间内变化梯度,提高收敛速度,可将输入输出数据变换在[0.1,0.9]或[0.2,0.8]区间内,这里取a=0.2,b=0.8。归一化结果如表1所示[9]。 表1 1985-2015年云南省农机总动力及其归一化结果 2.2GA-LM-BP神经网络基本参数的确定 BP神经网络的结构为标准的3层结构。据经验由连续4年的农机总动力预测下一年的农机总动力值,因而输入层的节点数为4,输出层的节点数为1。本文是以云南省1985-2015年的农机总动力作为训练样本,用[Xi,Xi+1,Xi+2,Xi+3]作为BP网络的输入样本,Xi+4作为输出样本,则输入样本为 输出样本为 本文预测模型采用tansig函数作为输入层到隐含层的传递函数,purelin函数作为隐含层到输出层的传递函数,trainlm函数作为训练函数。根据初始化参数设置原则及预测要求,经过多次训练,确定GA算法的遗传代数T=100,种群大小M=60,交叉概率Pc=0.4,变异概率Pm=0.08,BP神经网络的训练次数为1 000次,学习速率为0.05,训练目标为0.000 01,其余参数选择默认值。 以表1中云南省农机总动力的归一化数据作为样本建立GA-LM-BP神经网络模型进行仿真训练,并以相同的参数建立BP神经网络、LM-BP神经网络和GA-BP神经网络训练模型,训练完成后云南省农机总动力的真实值与预测值的结果如表2所示。 表2 预测结果 续表2 由表2的预测结果可以看出:以1985-2015年的云南省农机总动力作为训练样本,4种算法的预测值与真实值都较为一致,都有较好的预测精度。表2中,BP神经网络、LM-BP神经网络、GA-BP神经网络和GA-LM-BP神经网络的预测结果的平均相对误差分别为0.9266 74%、0.654 053%、0.493 122%和0.313 362%。可以明显看出:GA算法与LM算法都能提高BP神经网络的预测精度,而将GA算法与LM算法结合优化BP神经网络能得到更好的预测效果。这说明,GA-LM-BP神经网络有良好的预测能力。 因此,本文运用GA-LM-BP神经网络训练好的模型对云南省2016-2020年的农机总动力进行预测,通过反归一化计算后,其结果如表3所示。 表32016-2020年云南省农机总动力预测值 Table 3The predicted value of total power of Yunnan Province’s agricultural machinery during 2016-2020 年份农机总动力预测值/万kW20163439.4920173594.3920183724.0020193862.8420203952.78 在表3云南省农机总动力预测结果中,2016年云南省农机总动力达到3 439.49万kW,这与云南省农业厅提出的2016年全省预计新增农机总动力76万kW、达3 409万kW的数据较为吻合。云南省人民政府为贯彻落实国务院关于促进农业机械化和农机工业又好又快发展的要求,提出2020年全省农机总动力达4 000万kW的发展目标,与表3中预测2020年云南省农机总动力达到3 952.78万kW有少许差距。为了达到云南省2020年农机总动力的发展目标,在接下来的几年中云南省还需要提高农业机械化水平。 农机总动力是衡量农业机械化的重要指标之一,对其发展变化趋势进行准确预测能为农机化的发展规划提供科学的依据。本文提出了GA-LM-BP神经网络预测模型,结合GA算法的全局搜索寻优能力与LM算法的快速优化能力避免了BP神经网络易于陷于局部极小的情况。利用云南省1985-2015年农机总动力数据,建立GA-LM-BP神经网络预测模型,并与BP神经网络、LM-BP神经网络和GA-BP神经网络模型预测结果进行对比。预测结果中,基于4种算法的预测结果的平均相对误差分别为0.926 674%、0.654 053%、0.493 122%和0.313 362%,表明4种模型都有较好的预测性能。其中,组合型算法的精度明显优于单一算法,而3种算法的组合GA-LM-BP算法有最好的预测效果。因此,本文并通过GA-LM-BP神经网络训练好的模型对2016-2020年云南省农机总动力进行了预测,为云南省以后的农业机械发展规划提供理论依据。 参考文献: [1]王吉权,王福林,邱立春.基于BP神经网络的农机总动力预测[J].农业机械学报,2011,42(12):121. [2]张长胜,欧阳丹彤,岳娜,等.一种基于遗传算法和LM算法的混合学习算法[J].吉林大学学报:理学版,2008,46(4):675-677. [3]郭海如,李志敏,万兴,等.一种基于随机GA的提高BP网络泛化能力的方法[J].计算机技术与发展,2014,24(1):105-106. [4]刘春,马颖.遗传算法和神经网络结合的PSD非线性校正[J].电子测量与仪器学报,2015,29(8):1158. [5]李建伟,梁爱琴,田辉.2011-2015年河南省农业机械总动力的预测[J].农机化研究,2012,34(6):47-48. [6]黄豪彩,黄宜坚,杨冠鲁.基于LM算法的神经网络系统辨识[J].组合机床与自动化加工技术,2003 (2):7. [7]崔雪梅.基于灰色GA-LM-BP模型的CODMn预测[J].水利水电科技进展,2013,33(5):38-39. [8]中华人民共和国国家统计局.中国统计年鉴1986-2016[M].北京:中国统计出版社,1986-2016. [9]王吉权.BP神经网络的理论及其在农业机械化中的应用研究[D].沈阳:沈阳农业大学,2011. [10]董小艳.陕西农机化水平评价及耕种收机械化水平预测研究[D].杨凌:西北农林科技大学,2010.2 云南省农机总动力预测模型的建立


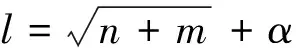
3 预测结果和分析



4 结论

