轻型钢−UHPC组合桥面板的疲劳可靠性评估
邓露,鲜亚兰,邵旭东
轻型钢−UHPC组合桥面板的疲劳可靠性评估
邓露,鲜亚兰,邵旭东
(湖南大学 土木工程学院,湖南 长沙,410082)
为了研究轻型钢−超高性能混凝土(UHPC)组合桥面板的疲劳可靠性,以广东虎门大桥为实例,建立局部梁段有限元模型,基于可靠度理论和疲劳累积损伤模型,计算并对比钢−UHPC组合桥面板和沥青混凝土铺装桥面板易疲劳开裂细节的疲劳可靠度,并研究UHPC层厚度等参数对轻型组合桥面板疲劳使用寿命的影响。研究结果表明:与沥青混凝土铺装桥面板相比,轻型组合桥面板可有效提高桥面板各疲劳细节的疲劳可靠度,延长其疲劳使用寿命;UHPC层厚度、交通量增长率以及车辆超载对轻型组合桥面板疲劳细节的疲劳使用寿命均有显著影响:当UHPC层厚度在一定范围(35~55 mm)时,厚度每增加10 mm,疲劳使用寿命至少延长37%;当年交通量增长率为5%时,疲劳使用寿命缩短超过45%;当车辆超载率为50%时,疲劳使用寿命缩短约70%。
疲劳可靠度;疲劳累积损伤模型;轻型组合桥面板;疲劳使用寿命
正交异性钢桥面板具有自身质量小、强度高、施工周期短、经济性能好等优点,已广泛应用于各类大跨径桥梁。然而,在车辆荷载反复作用下,正交异性钢桥面板易发生疲劳开裂[1−2],如英国Seven桥和我国虎门大桥均于建桥数年后便产生多处疲劳裂纹。为解决正交异性钢桥面板的疲劳开裂问题,SHAO等[3−4]将超高性能混凝土UHPC(即高弹性模量、高抗拉强度的配筋活性粉末混凝土)引入正交异性钢桥面,提出了“轻型组合桥面板”的结构形式。他们发现在车辆荷载作用下,铺设45 mm厚UHPC层的钢桥面疲劳细节处的应力峰值下降最高可达72%,显著提高了钢桥面的疲劳寿命。刘梦麟等[5]对轻型组合桥面板进行了理论分析和桥面板条带足尺模型疲劳实验,发现其具有良好的抗弯疲劳性能。丁楠等[6]对轻型组合桥面板的疲劳性能进行了研究,采用45 mm厚UHPC层的桥面板细节处的应力幅降幅最高可达82%,疲劳开裂风险可完全消除。然而,已有研究主要通过确定性分析方法对轻型组合桥面板的疲劳性能进行了分析,很少研究随机性因素的影响。在桥梁的服役期间,由于受车辆荷载、施工误差、环境腐蚀等随机性因素的影响[7],基于确定性分析方法预测的桥梁疲劳寿命可能不够准确,在这种情况下,基于可靠度理论预测的疲劳使用寿命将更加合理。为此,本文作者基于可靠度理论,考虑疲劳损伤累积的随机性,对轻型组合桥面板的疲劳可靠性进行评估。通过建立虎门大桥局部梁段ANSYS有限元模型,采用可靠度理论和疲劳累积损伤模型,计算和对比轻型组合桥面板和沥青混凝土铺装桥面板的易疲劳开裂细节的疲劳可靠度,并研究UHPC层厚度、交通量增长和车辆超载对轻型组合桥面板疲劳使用寿命的影响。
1 桥梁模型
1.1 虎门大桥简介
虎门大桥为1座主跨长为888 m的悬索箱梁桥,双向6车道,梁全宽35.60 m,箱梁高3.01 m,吊索间距12 m,面板厚12 mm,底板和斜腹板厚10 mm,钢箱梁每4 m设1道横隔板,板厚8 mm。U型加劲肋厚8 mm,高262 mm,开口宽314 mm。桥梁原铺装层为70 mm厚的SMA改性沥青混凝土,直接铺于钢箱梁面板上。轻型组合桥面板是在原钢箱梁上焊接长度为35 mm,直径为13 mm的剪力钉,并浇筑45 mm厚的UHPC层,见图1。

图1 2种桥面铺装体系
1.2 ANSYS有限元模型
由于钢桥面板应力主要来自于车辆荷载的作用,而车辆荷载效应的影响范围有限[8],因此,本文仅建立虎门大桥钢箱梁局部梁段的ANSYS有限元模型,纵桥向截取两吊索间的3跨横隔板,横桥向截取半幅箱梁,见图2。钢板(弹性模量为210 GPa,泊松比为0.3)采用4节点shell63单元,UHPC层(弹性模量为42.6 GPa,泊松比为0.2)、沥青混凝土铺装层(弹性模量为2 GPa,泊松比为0.3)以及磨耗层(弹性模量为2 GPa,泊松比为0.3)均采用8节点solid45单元[5, 9]。值得一提的是,本文分析的重点在于UHPC结构层对钢桥面板疲劳性能的影响。因此,为简化分析,在建模过程中并未考虑轻型组合桥面板的钢筋和剪力钉,而是通过耦合命令将铺装层与钢板连为整体[5]。SHAO等[4, 6]的疲劳试验研究结果表明,此类钢−UHPC组合桥面板的破坏形式均为钢桥面板先开裂,并未观测到剪力钉以及钢−UHPC粘结层的破坏。

图2 钢箱梁横截面及局部梁段模型
2 钢桥面疲劳应力分析
2.1 疲劳验算细节
正交异性钢桥面板构造复杂,焊缝密集,易疲劳开裂。本文选择工程实践中常见的易疲劳开裂细节作为研究对象[6],见图3。
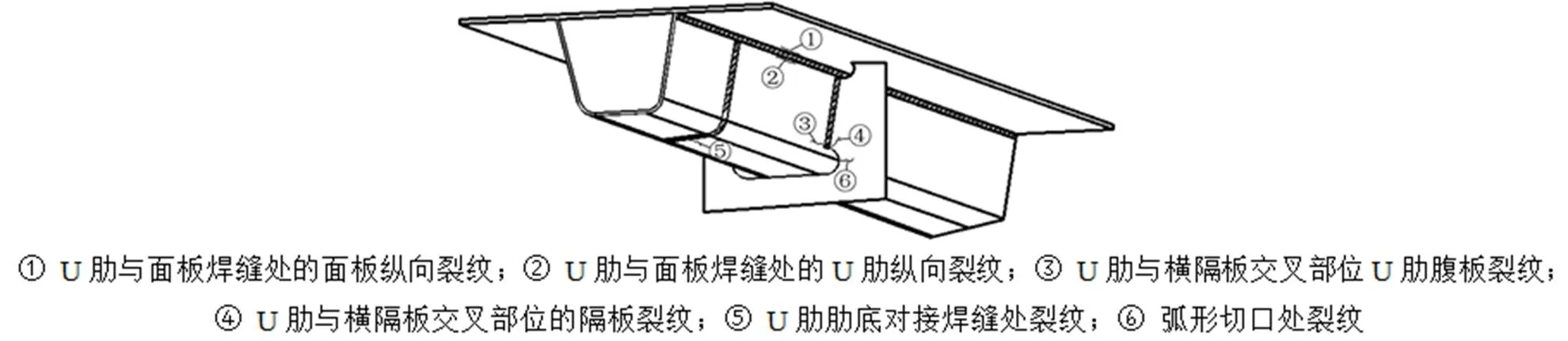
图3 正交异性钢桥面板的易疲劳开裂细节
2.2 疲劳荷载计算模型
根据JTG D64—2015“公路钢结构桥梁设计规范”的相关规定,采用疲劳荷载计算模型Ⅲ(见图4)作为车辆荷载进行疲劳验算。根据交通规则和行车习惯,重型车辆主要行驶在慢车道和中车道上。车辆荷载在虎门大桥有限元模型上加载时中车道的细节应力大于慢车道的应力[10],因此,选择在中车道进行加载,且每次仅加载1辆疲劳车。对于横向分布的影响,仅考虑轮迹横向最不利位置所在车道的轮载贡献[11]。桥梁动力冲击系数取0.15以考虑车辆动力效应的影响[8]。

图4 疲劳荷载计算模型Ⅲ
2.3 疲劳细节应力分析
疲劳荷载模型加载时,采用移动面荷载加载的方式,车轮着地面积为0.2 m×0.6 m,每次移动0.2 m,获得疲劳车从驶入车道至驶出的应力历程,然后,通过雨流计数法获得疲劳应力幅值谱。本文分别计算轻型组合桥面板和沥青混凝土铺装桥面板易疲劳开裂细节的应力,计算结果见表1。从表1可见:与沥青混凝土铺装桥面板相比,轻型组合桥面板对钢桥面板与U肋连接处疲劳细节的应力影响显著,各疲劳细节的应力均有不同程度降低,面板处的最大应力下降高达74%,最大应力幅降幅高达83%。

表1 疲劳细节应力提取方向、最大应力及最大应力幅值
注:名义应力提取方向参照文献[8];′与U肋腹板倾斜方向平行;1为第一主应力;“−”表示压应力。
需要注意的是:表1中疲劳细节的应力幅降幅是指轻型组合桥面板相对于沥青混凝土铺装桥面板的降幅,而文献[6]中的降幅为轻型组合桥面板相对于无铺装层的纯钢桥面板的降幅。由于沥青混凝土铺装层也可以在一定程度上降低钢桥疲劳细节的应力幅[9],因此,表1中的降幅比文献[6]中的降幅要小。
UHPC层的峰值拉应力为13.8 MPa,小于GDJTG/T A01—2015“超高性能轻型组合桥面板结构技术规程”规定的弯拉应力容许值29.4 MPa,故UHPC层抗弯拉疲劳性能能够满足规范要求。
3 疲劳可靠性分析
3.1 极限状态方程
基于疲劳累积损伤模型进行疲劳可靠性分析,以应力循环次数为变量,疲劳细节的极限状态方程表示为[12]

式中:c为疲劳细节达到疲劳破坏的临界状态时所经历的应力循环总数;为疲劳细节已经历的应力循环总数。
根据S-N曲线和Miner线性累积损伤准则可得

其中:

c为Miner疲劳累积损伤临界值;和为材料疲劳细节常数;re为变幅荷载的等效应力幅,本文计算时略去了小于1 MPa的应力幅[13];i为第个应力幅值; n为疲劳细节在应力幅S作用下实际应力循环次数。
根据Miner线性累积损伤准则,当疲劳累积损伤值大于累积损伤临界值c时,即发生疲劳失效。由式(1)和式(2),在变幅荷载作用下,疲劳细节的极限状态方程可改写为

3.2 参数统计分布特性
由于国内暂时没有对疲劳细节常数的统计分布特性进行研究,因此,各细节类别参考AASHTO LRFD(2012)(以下简称“美国规范”)的分类。根据文献[14],疲劳细节常数服从对数正态分布,疲劳统计参数见表2;取定值3.0。根据WIRSCHING[15]的疲劳实验研究,Miner累积损伤临界值c服从均值μc为1.0,变异系数δc为0.3的对数正态分布。

表2 疲劳细节常数C的统计参数
根据美国规范,应力循环次数与服役年限的关系为

式中:ADFT为1个车道的日平均疲劳车交通量;s为1辆车过桥所产生的应力循环次数。参照美国规范,对于正交异性桥面细节,s取为5.0。
参考美国规范和已有研究[10, 16],假设:1) 在总交通量中,只有20%的汽车会引起构件疲劳损伤;2) 疲劳车的双向通行量相等,只在中车道和慢车道上行驶,且慢车道与中车道的疲劳车通行量比为4:3。1997—2008年,虎门大桥的日平均交通量大约为34 000 辆[17],其中会引起桥梁构件疲劳的单向车辆数为3 400辆。本文偏保守地选择慢车道疲劳车通行量计算,ADFT取为2 000辆。
3.3 疲劳可靠度指标计算
根据极限状态方程,正交异性钢桥面结构细节疲劳失效的概率为

根据各参数的统计分布特性,采用一次二阶矩法,可得疲劳细节的可靠指标表达式[12]:


虎门大桥的设计使用年限取为100 a。通过上述疲劳可靠度的计算方法,可得到设计使用年限内采用不同桥面形式的疲劳细节的疲劳可靠度变化规律,计算结果如图5所示。关于疲劳目标可靠指标target的取值,目前国内相关规范并没有明确的规定,且美国规范中也没有提及仅针对疲劳分析的目标可靠指标,因此,本文采用ISO 2394:1998(E)[18]规定的结构构件失效目标可靠指标2.3。本文的疲劳使用寿命为验算细节的疲劳可靠指标随时间减小到目标可靠指标时的服役年限[19]。

图5 疲劳细节的疲劳可靠指标与桥梁服役年限的关系
由图5可知:总体上,随着桥梁服役年限增加,桥梁疲劳可靠指标逐渐降低。采用70 mm厚沥青混凝土铺装层的钢桥面验算细节①,②,③和④的疲劳可靠指标均在服役后10 a左右降低至target。与沥青混凝土铺装桥面板相比,轻型组合桥面板可以有效提高各疲劳验算细节的疲劳可靠度,延长其疲劳使用寿命。细节①在服役时间达到设计使用年限(100 a)时的疲劳可靠度为8.78(远高于target),疲劳使用寿命大幅度延长,疲劳开裂风险可基本消除;其余细节的疲劳使用寿命也延长了10~40 a。
4 参数分析
4.1 UHPC层厚度
已有研究表明[10],30~60 mm厚的UHPC层能基本满足轻型组合桥面板的性能要求。为了研究UHPC层厚度对轻型组合桥面板疲劳使用寿命的影响,取UHPC层厚度分别为35,45和55 mm,计算结果见 表3。
由表3可知:当UHPC层厚度为35~55 mm时,厚度每增加10 mm,疲劳细节的疲劳使用寿命至少延长37%;当UHPC层厚度为35 mm时,细节①在服役时间达到设计使用年限(100 a)时的疲劳可靠指标为6.91,仍远高于target;细节③和细节④的疲劳可靠指标在服役后15 a左右最先达到target,但仍大于图5中的70 mm厚的沥青混凝土铺装层服役时间。

表3 UHPC层厚度对疲劳使用寿命的影响
注:括号内为服役时间达到设计使用年限100 a时的疲劳可靠指标。
4.2 交通量
交通量增大会导致应力循环次数增加,设运营初期的日平均疲劳车交通量为0,年交通量增长率为,则应力循环次数变为

虎门大桥第1年日平均交通量约为15 000辆[17],按照3.2节叙述方法估算出0为900辆。本文考虑年交通量增长率分别为2%和5%时对轻型组合桥面板疲劳使用寿命的影响,计算结果见表4。

表4 交通量增长对疲劳使用寿命的影响
注:括号内为服役时间达到设计使用年限100 a时的疲劳可靠指标。
由表4可知:年交通量增长率对轻型组合桥面板的疲劳使用寿命影响显著。当年交通量增长率为5%时,除细节①外的其余细节的疲劳使用寿命比交通量未增长时的疲劳使用寿命缩短超过45%;细节①的疲劳可靠指标在服役时间达到设计使用年限(100 a)时仍高于target;细节③和细节④处的疲劳可靠度在服役后25 a左右仍最先达到target。
4.3 车辆超载
为了研究车辆超载对轻型组合桥面板疲劳使用寿命的影响,将疲劳荷载计算模型Ⅲ中的轴重分别增加20%和50%进行分析,计算结果见表5。
由表5可知:考虑车辆超载时,细节①的疲劳可靠指标在服役时间达到设计使用年限(100 a)时仍远高于target;当车辆超载率为50%时,除细节①外的其余细节的疲劳使用寿命比未考虑超载时缩短约70%,其中细节③和细节④的疲劳可靠指标达到target的服役时间缩短至7 a左右。实际上,虎门大桥货车的超载现象非常严重,轴重最大甚至达到设计值的4倍以 上[20],极大地加速了桥梁的疲劳破坏。

表5 车辆超载对疲劳使用寿命的影响
注:括号内数据为服役时间达到设计使用年限100 a时的疲劳可靠指标。
5 结论
1) 与沥青混凝土铺装桥面板相比,轻型组合桥面板可有效提高各疲劳细节的疲劳可靠度,延长其疲劳使用寿命,纵肋与面板连接处的面板细节处疲劳开裂风险可基本消除,其余细节处的疲劳使用寿命延长10~40 a。
2) UHPC层厚度、交通量增长以及车辆超载对轻型组合桥面疲劳细节的疲劳使用寿命均有显著影响。当UHPC层厚度在一定范围(35~55 mm)时,厚度每增加10 mm,疲劳使用寿命至少延长37%;当年交通量增长率为5%时,疲劳使用寿命缩短超过45%;当车辆超载率为50%时,疲劳使用寿命缩短约70%。我国货车超载的车辆比例约占到60%,超载率30%以上的车辆达到18%~22%,超载率为100%的车辆达到2.5%~10.0%。因此,控制超载对保证桥梁的设计使用寿命非常关键。
3) 在车辆荷载作用下,轻型组合桥面板的横隔板与U肋连接处细节更易疲劳受损。建议对横隔板与U肋连接处各细节处采取局部加强措施,如增大横隔板厚度、缩短横隔板间距等。
4) 本文的车辆荷载采用的是规范中的疲劳荷载计算模型,且将车辆动力效应取为常数,这与实际情况可能存在一定差异,有待进一步研究。
[1] PFEIL M S, BATTISTA R C, MERGULHAO A J R. Stress concentration in steel bridge orthotropic decks[J]. Journal of Constructional Steel Research, 2005, 61(8): 1172−1184.
[2] KOLSTEIN M H. Fatigue classification of welded joints in orthotropic steel bridge decks[D]. Delft: Delft University of Technology. College of Structural and Building Engineering, 2007: 12−15.
[3] 邵旭东, 曹君辉, 易笃韬, 等. 正交异性钢板−薄层RPC组合桥面基本性能研究[J]. 中国公路学报, 2012, 25(2): 40−45. SHAO Xudong, CAO Junhui, YI Dutao, et al. Research on basic performance of composite bridge deck system with orthotropic steel deck and thin RPC layer[J]. China Journal of Highway and Transport, 2012, 25(2): 40−45.
[4] SHAO Xudong, YI Dutao, HUANG Zhenyu, et al. Basic performance of the composite deck system composed of orthotropic steel deck and ultrathin RPC layer[J]. Journal of Bridge Engineering, 2013, 18(5): 417−428.
[5] 刘梦麟, 邵旭东, 张哲, 等. 正交异性钢板−超薄RPC组合桥面板结构的抗弯疲劳性能试验[J]. 公路交通科技, 2012, 29(10): 46−53.LIU Menglin, SHAO Xudong, ZHANG Zhe, et al. Experiment on flexural fatigue performance of composite deck system composed of orthotropic steel deck and ultra-thin RPC layer[J]. Journal of Highway and Transportation Research and Development, 2012, 29(10): 46−53.
[6] 丁楠, 邵旭东. 轻型组合桥面板的疲劳性能研究[J]. 土木工程学报, 2015, 48(1): 74−81. DING Nan, SHAO Xudong. Study on fatigue performance of light-weighted composite bridge deck[J]. China Civil Engineering Journal, 2015, 48(1): 74−81.
[7] KWON K, FRANGOPOL D M. Bridge fatigue reliability assessment using probability density functions of equivalent stress range based on field monitoring data[J]. International Journal of Fatigue, 2010, 32(8): 1221−1232.
[8] 童乐为, 沈祖炎. 正交异性钢桥面板疲劳验算[J]. 土木工程学报, 2000, 33(3): 16−21. TONG Lewei, SHEN Zuyan. Fatigue assessment of orthotropic steel bridge decks[J]. China Civil Engineering Journal, 2000, 33(3): 16−21.
[9] 吕韶全. 桥面铺装对正交异性钢桥面板疲劳性能的影响[D]. 长沙: 中南大学土木工程学院, 2014: 26−35. LV Shaoquan. Influence of pavement on fatigue performance of orthotropic steel deck[D]. Changsha: Central South University. College of Civil Engineering, 2014: 26−35.
[10] 丁楠. 超高性能混凝土对轻型组合桥面结构疲劳使用寿命的影响研究[D]. 长沙: 湖南大学土木工程学院, 2014: 53−54. DING Nan. Study on influence of ultra-high performance concrete on light-weighted composite bridge deck[D]. Changsha: Hunan University. College of Civil Engineering, 2014: 53−54.
[11] 卜一之, 杨绍林, 崔闯, 等. 轮迹横向分布对钢桥面板疲劳应力幅的影响[J]. 桥梁建设, 2015, 45(2): 39−45. BU Yizhi, YANG Shaolin, CUI Chuang, et al. Influence of wheel trace transverse distribution on fatigue stress ranges of steel deck[J]. Bridge Construction, 2015, 45(2): 39−45.
[12] CHUNG H. Fatigue reliability and optimal inspection strategies for steel bridges[D]. Texas: The University of Texas at Austin. Cocrkrell School of Engineering, 2004: 60−68.
[13] 孙传智, 李爱群, 缪长青, 等. 考虑随机交通流量的润扬大桥钢箱梁疲劳失效概率及可靠度评估[J]. 中外公路, 2012, 32(2): 93−97. SUN Chuanzhi, LI Aiqun, MIAO Changqing, et al. Fatigue failure probability and reliability assessment of Runyang bridge steel box girder considering the random traffic flow[J]. Journal of China & Foreign Highway, 2012, 32(2): 93−97.
[14] LIU Ming, FRANGOPOL D M, KWON K. Fatigue reliability assessment of retrofitted steel bridges integrating monitored data[J]. Structural Safety, 2010, 32(1): 77−89.
[15] WIRSCHING P H. Fatigue reliability for offshore structures[J]. Journal of Structure Engineering, 1984, 110(10): 2340−2356.
[16] 李乔, 唐亮, 裴岷山, 等. 大跨径公路钢斜拉桥索梁锚固区疲劳试验荷载研究[J]. 公路, 2004, 27(12): 7−10. LI Qiao, TANG Liang, PEI Minshan, et al. Load research of long-span highway steel beam cable-stayed bridge fatigue test[J]. Highway, 2004, 27(12): 7−10.
[17] 周怡斌. 公路大桥正交异性钢桥面板裂缝成因研究及局部疲劳分析[D]. 北京: 清华大学土木工程系, 2010: 27−28. ZHOU Yibin. Crack study and local fatigue analysis of orthotropic steel decks on bridges[D]. Beijing: Tsinghua University. Faculty of Civil Engineering, 2010: 27−28.
[18] ISO 2394:1998(E), General principles on reliability for structures[S].
[19] 邓扬, 李爱群, 刘扬, 等. 钢桥疲劳荷载效应监测数据概率建模与疲劳可靠性分析方法[J]. 土木工程学报, 2014, 47(7): 79−87.DENG Yang, LI Aiqun, LIU Yang, et al. Probabilistic modeling of fatigue loading effects and fatigue reliability evaluation for steel bridge based on monitored date[J]. China Civil Engineering Journal, 2014, 47(7): 79−87.
[20] 王迎军, 朱桂新, 陈旭东. 虎门大桥钢桥面铺装的使用和维护[J]. 公路交通科技, 2004, 21(8): 64−67. WANG Yingjun, ZHU Guixin, CHEN Xudong. The using and maintenance of the steel deck pavement in Humen bridge[J]. Journal of Highway and Transportation Research and Development, 2004, 21(8): 64−67.
(编辑 陈灿华)
Fatigue reliability assessment of light-weighted steel−UHPC composite bridge deck
DENG Lu, XIAN Yalan, SHAO Xudong
(School of Civil Engineering, Hunan University, Changsha 410082, China)
In order to investigate the fatigue reliability of a light-weighted composite bridge deck consisting of a steel deck and an ultra-high performance concrete (UHPC) structural layer, a finite element model for a girder segment of the Humen Bridge in Guangdong Province was established. The fatigue reliability indexes of typical fatigue-prone details of the steel−UHPC composite bridge deck and the asphalt concrete pavement bridge deck were calculated and compared, and the influence of a few parameters including the UHPC layer thickness on the fatigue life of light-weighted composite bridge deck was investigated based on the reliability theory and fatigue cumulative damage model. The results show that compared to the asphalt concrete pavement bridge deck, the light-weighted composite bridge deck can effectively increase the fatigue reliability of fatigue-prone details and extend the fatigue life of the light-weighted composite bridge deck. UHPC layer thickness, traffic volume growth and vehicle overloading rate have a significant impact on the fatigue life of the fatigue details of the light-weighted composite bridge deck. A 10 mm increment of UHPC layer thickness (within range of 35−55 mm) can extend the fatigue life by at least 37%; 5% annual traffic volume growth rate can reduce the fatigue life by more than 45%, and 50% vehicle overloading rate can reduce the fatigue life by about 70%.
fatigue reliability; fatigue cumulative damage model; light-weighted composite bridge deck; fatigue life
U443.32
A
10.11817/j.issn.1672-7207.2018.03.026
1672−7207(2018)03−0711−07
2017−03−10;
2017−06−12
国家自然科学基金资助项目(51478176);湖南省杰出青年基金资助项目(14JJ1014) (Project(51478176) supported by the National Natural Science Foundation of China; Project(14JJ1014) supported by the Outstanding Youth Foundation of Hunan Province)
邓露,博士,教授,从事车桥耦合振动、桥梁结构安全等研究;E-mail: denglu@hnu.edu.cn

