基于Hessian矩阵的角点自动检测算法

寇冬晨, 韩　瑜, 顾　浩

(江苏自动化研究所， 江苏 连云港　222061)

近几年来,摄像机标定技术广泛应用于各个领域,如机器人焊接、三维测量、视觉导航等。摄像机标定技术通过大量采集实际物点在世界坐标系下与图像坐标坐标系下相对应的坐标,创建了相机的数学模型,计算出模型参数,从而建立了世界坐标系与图像坐标系间的转换关系。由此可见,标定过程中对于所使用的棋盘格角点识别的精确度将大大影响摄像机标定结果的准确性。Smith等人曾提出[1],图像上即使是很小的像素误差,也会使最终的标定参数产生非常大的误差。因此,角点识别的精确度是摄像机标定的关键。

主流的角点检测算法大致分为两类:自动检测算法和人工交互法。前者主要是利用了角点附近区域灰度变化较大这一特点,通过设计不同的角点检测算子,如Harris检测算子[2]、SUSAN[1]检测算子等,根据最终的算子检测结果来计算角点的位置。这一方法虽然在一定程度上解决了摄像机标定的自动化问题,但仍然存在伪角点剔除的问题,标定结果会因为伪角点的存在而受到很大的影响。后者则是通过人机之间的交互,如利用键盘或鼠标等外设输入或点击获取角点的位置,这一方法过于依靠操作人员的经验,往往会存在一些人为取点上的误差,且由于是依靠手动操作选取角点,当角点过多时,取点耗时将大大增加,从而大幅度降低了摄像机标定的效率。对于上述问题,国内外多位学者都进行了针对性的研究。郝颖明等[3]巧妙地将角点检测和角点排序结合起来,通过角点检测算子与区域能量中心共同实现了角点的精确定位,该算法计算量较大,对于大畸变图像很难有较好的角点提取效果。刘嵩等[4]提出了一种基于单应性矩阵的棋盘格角点检测算法,该算法有较好的精确性和鲁棒性,但其通用性不强。鉴于以上各种问题,本文以各种角点提取算法为基础,提出了一种改进的基于Hessian矩阵的角点检测算法。

1　Hessian矩阵角点自动检测算法

在摄像机标定过程中用到的棋盘格通常是由一个个方形格组成的,这些方格依次呈黑白色错落排列,角点即为黑白格子的相交点。图1中n1和n2为图像灰度函数r(x,y)的二阶方向导数的最大值和最小值。

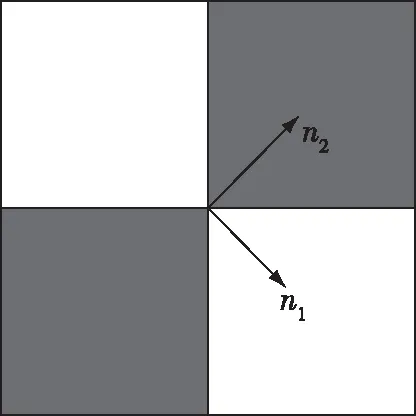
图1　二阶方向导数单位向量

图2　差分模版

对于Hessian矩阵H,其特征值表达式如下:

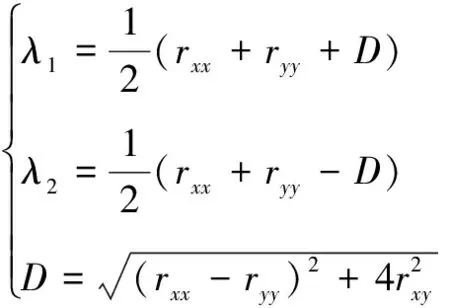
(1)

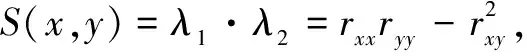
在通常情况下,上文提及的阈值Th0为固定阈值[6],是由操作人员不断重复试验,不断调整阈值Th,直到达到最好的角点识别结果后才得到的。这样做不仅需要耗费大量时间,同时还过于依靠操作人员自身的经验,这就使得固定阈值的角点检测法应用范围小,不能灵活自动地调节以适应多噪声环境,尤其是在日益智能化的机器视觉中,其不足之处愈发明显[6-8]。本文提出了一种自适应阈值法，首先对形状算子S取反,对于所有取反后形状算子大于0且在领域内最大的形状算子依次排序,其结果为(S1,S2,…,Sn)。再对排序后的形状算子做如下运算:

Diff=(S2-S1,S3-S2,…,Sn-Sn-1)

(2)

设所得的差值Diff的最大值对应的形状算子为Sd,则所选的阈值Th0为Th0=ε·Sd,1<ε<2,举例说明该自适应阈值法。图3(a)为实验所使用的棋盘格原始图像,图3(b)的横纵坐标分别为差值Diff和像素点编号。如图3(b)所示,Diff取最大值处的像素点编号为307050,而此点的形状算子值为102.55。不妨设ε=2,当检测到的角点数小于真实角点数时,ε=ε-0.05,如此不断重复运算,直到检测角点数与真实角点数相近为止。通过以上运算可得ε=1.05,则自适应阈值Th0=107.68。那么,对于所有的形状算子来说,凡是在5×5的检测窗口中取得最大值且大于107.68的形状算子,其所对应的像素点即为棋盘格上的角点。利用这种方法,可以达到滤除绝大部分伪角点的效果,不仅较为完整地保留了所有棋盘格上的角点,同时最大限度地抑制了大部分干扰点,如图4所示。

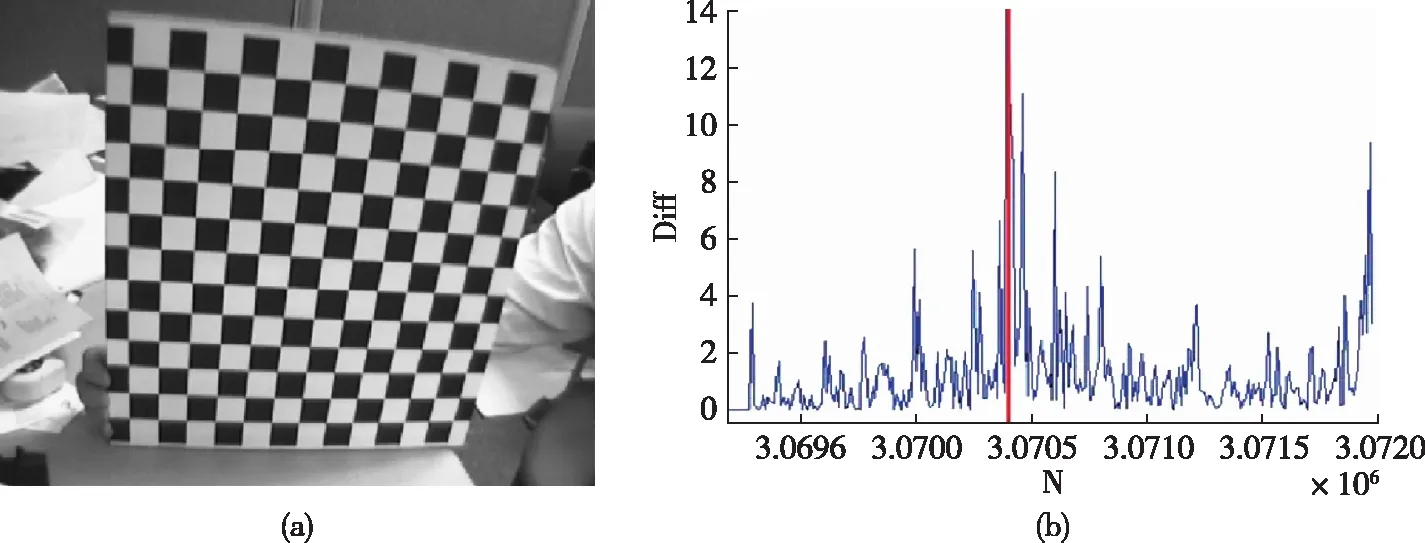
图3　棋盘格原始图像和形状算子差值Diff

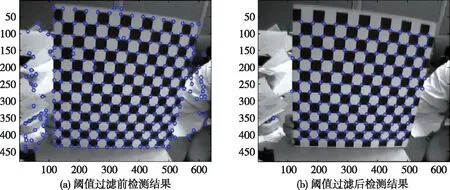
图4　自适应阈值过滤结果比较

2　伪角点剔除

由上文可知,在进行自适应阈值过滤后,虽然剔除了大部分的伪角点,但仍有少部分的与真角点极为相似的伪角点存在,这些伪角点虽然数量较少,但其仍旧会影响后续的角点识别结果,造成世界坐标系与图像坐标之间的转换关系出现偏差,从而影响摄像机的标定结果。因此,这些伪角点也必须予以剔除。本文根据棋盘格角点的特性[9],采用了圆形对称模版剔除伪角点,如图5所示。

图5　棋盘格角点和圆形对称模版

由图5可知,首先将圆形模版平均分为8个区域,并依照逆时针方向对这8个区域进行编号。其次,对圆形模版中的各个扇区中的像素进行灰度值累加,并计算整个模版区域中的平均像素灰度值记为Im,各个扇区的灰度值记为Ii。最后根据棋盘格角点的邻域对称性[10],可推得当圆形模版中心与真角点重合时,圆形模版中心对称的各个区域的灰度值应为相近值,即Ii≈Ii+4(i=1,2,3,4),(Ii-Im)与(Ii+4-Im)正负相同,可得:

Ti=(Ii-Im)·(Ii+4-Im)>T

(3)

实际操作中,由于圆形模版的中心位置不一定与角点重合[11],可能存在一定的偏差,这也就导致了8个扇区不再是严格地中心对称,使得某些真实角点也会被当作伪角点遭到剔除。因此,需要对T进行处理,不妨取T=-η·Tm。Tm为Ti的平均值。初始时取η=1,不断循环计算,当大部分伪角点被剔除后,如果检测到的角点数小于真实角点数,则η=η+1;如果检测到的角点数大于等于真实角点数,则η=η-0.1,如此循环判断,直到检测到的角点数与真实角点数相差不大为止。

3　实验结果与分析

本文采用中国大恒有限公司生产的DH-SV2000FC工业摄像机,该摄像机的最大分辨率为1628×1236,焦距为60mm,像素尺寸为4.2μm×4.2μm。所采用的棋盘格靶标尺寸为200mm×200mm,该棋盘格靶标包含60×60个黑白方块,每个黑白方块的尺寸为3mm×3mm。

考虑到目前市面上大多数的机器视觉所采用的标定方法都是张广军棋盘格标定法[12],该种标定方法较为成熟,精度较高,鲁棒性好,且其在大多数情况下都有较好的角点识别结果。因此本文主要比较自适应阈值检测法与张广军检测法。如图6所示,对于三张不同环境下(全景图,复杂背景图及无干扰图)拍摄到的照片分别进行两种不同的角点检测方法,表1为二者的检测结果对比。

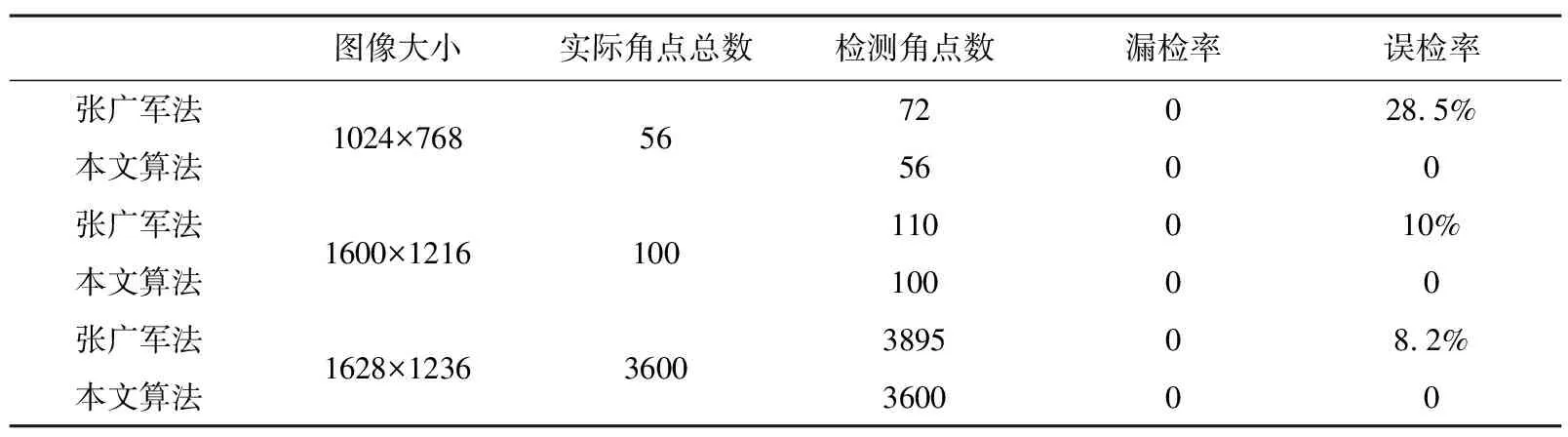
表1　张广军算法与本文算法结果对比

图6　张广军算法与本文算法结果对比

由以上数据可以看出张广军算法虽然不存在漏检率,但其误检率要高于本文算法,原因就在于张广军算法中采用了固定阈值的经验检测方法,这种方法过于死板,灵活性不足,不能够胜任不同场景下的多种视觉标定工作。而本文则较好地完成了角点检测,在3个典型实验测试中,误检率为零,突出了其较为优越的角点识别性能。

4　结束语

本文提出了一种改进的基于Hessian矩阵的自动角点检测算法,相对于固定阈值这一传统方法,自适应阈值法具有更高的准确度和灵活性,不再依赖于操作人员的经验,很好地避免了人为造成的标定偏差,提高了算法的适用性和稳定性;同时本文还依据角点邻域的中心对称特性,采用圆形模版剔除剩余部分的伪角点,提高了算法对于真实角点的识别准确性。除此之外,本文通过实际实验证明,在不同场景下(全景图,复杂背景图及无干扰图)本文算法具有更高的角点识别准确率,既不受复杂背景环境下的伪角点干扰,又不会因广角镜头产生的畸变而影响角点识别的准确率。所以本文算法对于摄像机标定具有较为重要的实际意义,对于展开后续的图像测量、三位重构等具有重要的指导作用。

参考文献:

[1]SMITH S M, BRADY M. SUSAN—a new approach to level image processing[J]. International Journal of Computer Version,1997,23(1):45-78.

[2]HARRIS C, STEPHENS M. A combined corner and edge detector[C]∥Proceedings of the 4th Alvey Vision Conference. Sheffield: University of Sheffield Printing Office, 1988: 147-151.

[3]郝颖明,朱枫.摄像机在线标定中的棋盘格角点自动检测方法[J].计算机工程,2007,17(9): 213-215

[4]刘嵩, 叶玉堂. 基于单应性矩阵的棋盘格角点检测研究[J]. 电子设计工程, 2012, 3(6):114-115.

[5]谭晓波. 摄像机标定及相关技术研究[D]. 长沙：国防科学技术大学, 2004.

[6]YANG Xing-fang,HUANG Yu-mei,GAO Feng. A simple camera calibration method based on sub-pixel corner extraction of the chessboard image[C]∥IEEE International Conference,2010(3):688-692.

[7]Ren M, Yang W, Yang J. A New and Fast Contour-filling Algorithm[J]. Pattern Recognition, 2005, 38(12): 2564-2577.

[8]陈传波,陆枫. 计算机图形学基础[M]. 北京：电子工业出版社, 2002: 127-128.

[9]Arrospide J,Salgado L,Nieto M,Vehicle detection and tracking using homography-based plane rectification and particle filtering[R]. San Diego:Intelligent Vehicles Symposium(IV),2010: 150-155.

[10] Ma S D, A self-calibration technique for active vision systems. IEEE Transactions on Robotics & Automation, 1996, 12(1); 114-120.

[11] ZHANG Y J, Fast approach to checkerboard corner detection for calibration[J]. Optical Engineering, 2014, 53(11):112203.

[12] 张广军. 机器视觉[M].北京：科学出版社, 2005.