利用径向衍射研究β-Mo B2的强度和状态方程

熊 伦

0　引言

压力作为一个重要的热力学物理量,在凝聚态物质研究中起着重要的作用.它可以改变物质中原子之间的距离,使得原子按照更加紧密的方式堆积,进而改变其结构及物理、化学等相关性质,如:高压结构相变、高压下的金属化相变、高压铁电以及软膜相变等.由于三维B-B键的引入,[1-3]过渡金属和硼元素形成的化合物被认为是潜在的超硬材料.[4-6]Ti B2、ReB2和WB2维氏硬度的范围是26GPa到30GPa.[6-8]一般而言,T MB2(Mo B2、WB2、Tcb2、ReB2、Ru B2、Os B2)具有和Al B2相似的结构,空间群是P 6/mmm.[9-13]β-MOB2具有菱面体结构,其空间群是R-3m.WB2具有六方结构,其空间群是P63/mmc.随后,β-MOB2的高压结构成为研究的重点[10,14-17].Fr otscher等人通过中子衍射实验最先报道了Mo2B5实际上应该是Mo2B4.[10]Zhang等人理论计算了β-MOB2的体弹模量和维氏硬度,[14]分别为324 GPa和21.3 GPa.Liang等人用第一性原理计算研究了β-MOB2的结构稳定性、力学性质、晶体结构和电子结构.[15]作者指出其体弹模量和维氏硬度分别为312 GPa和33.1 GPa.Tao等人在高温高压条件下成功地合成了纯相β-MOB2.[16]作者第一次测量得到了β-MOB2的维氏硬度为22.0 GPa.Yin等人同样在高温高压条件下合成了β-MOB2,[9]在加载为49 N时测得其维氏硬度为21 GPa.此外,作者通过超声波测量得到了β-MOB2的体弹模量和剪切模量分别为296 GPa和190 GPa.Liu等人用同步辐射X射线衍射实验加压到24GPa,获得的体弹模量和其一阶导数分别为314(11)GPa和6.4(15).[17]

本文中,结合晶格应变理论和第一性原理计算得到的高压下剪切模量,[18,19]用角度色散X射线径向衍射实验研究了β-MOB2到82 GPa的强度和状态方程.

1　实验设计

纯相的β-MOB2由钼粉和硼粉通过热压法合成.根据室压下粉末X射线衍射结果,[16]合成的β-MOB2具有菱面体结构(空间群是R-3m,见图1),晶胞参数是a=3.011629Å和c=20.943118Å.选用台面直径为250微米的两柱全景金刚石对顶砧(DAC)进行径向衍射实验.预压铍封垫到约20GPa,使其厚度约为25微米,并在压痕的正中间打大小为50微米的样品孔.将β-MOB2片放到样品孔中,随后放一个直径约为30微米的钼片到样品上表面.钼片被用于压标和样品位置参考.[20]为了增大剪切力,本实验不加传压介质.实验中DAC转过28度以减小Be封垫的衍射峰影响.[21]

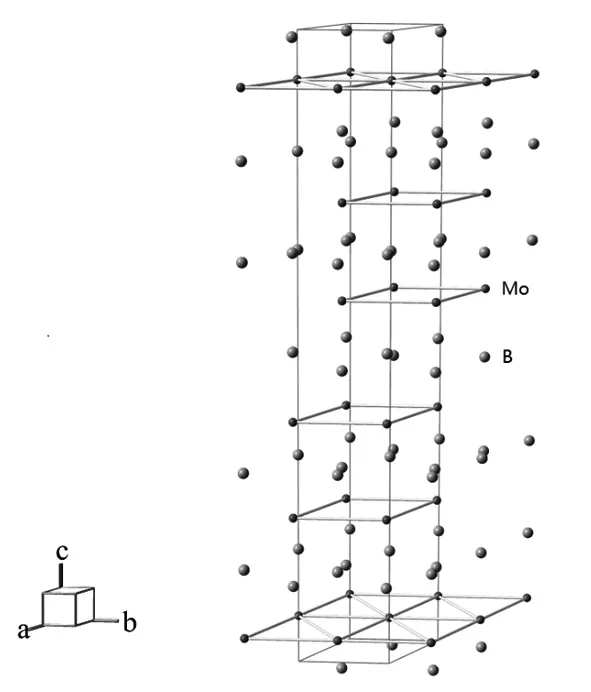
图1　β-MOB2的晶格结构

原位高压X射线径向衍射实验在北京同步辐射装置4 W2实验站上完成.实验的单色光波长是0.6199埃,半高全宽是30(水平)×12(垂直)微米2.衍射谱由Mar345成像板接收,接收到的数据由Fit2D软件进行分析.[22]径向衍射每个压力点在采谱前先放置30分钟使样品中的应力得到充分释放,随后采谱,采谱时间为15到20分钟.

2　理论介绍

X射线径向衍射数据用Singh等人提出的晶格应变理论进行分析.[18,19]根据该理论,测得的

dm(hkl)是y角(金刚石对顶砧加压方向和hkl衍射面法向的夹角)的函数,可以表示为:

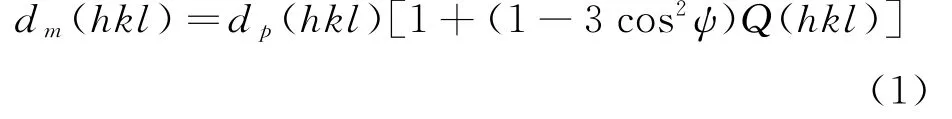
其中dm(hkl)是测得的d值,dp(hkl)是静水压环境下的d值.

公式(1)中的y表示为:

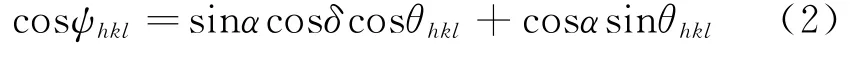
其中q是衍射角,d是成像板中的几何角度,a等于28度(径向衍射实验将DAC转过28度).

公式(1)中的Q(hkl)是晶格应变,可以表示为:

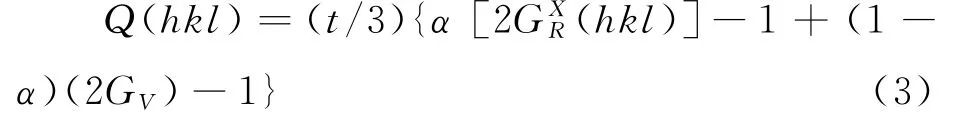
G是剪切模量,下标R和V分别表示Reuss近似(压力连续)和Voigt近似(应变连续).上标X表示由于不同的hkl引起的平均效应.α确定了Reuss近似和Voigt近似的比重.

对于六方晶系,[19]

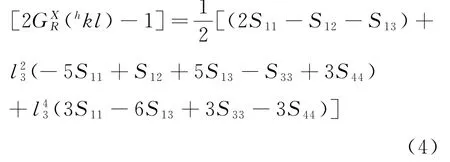
其中l23=3a2l2/M2,M2=[4c2(h2+hk+l2)+3a2l2],a和c六方晶胞的晶胞参数.

在绝大多数高压实验中,令a=1.由此,差应力的公式可以推导出来:

表示所有Q(hkl)的平均值.G是粉末样品的剪切模量,而且G可由超声波结果外推和理论计算得到.

3　结果与讨论

3.1　数据处理

采集得到的衍射谱用Fit 2D软件处理,[22]再用Multif uit 4.2软件进行进一步分析.选择衍射环从90度到180度,每5度进行积分.β-MOB2的径向衍射实验研究到82GPa,压力由钼压标给出.[20]

图2为径向衍射不同压力下y=54.7°时的衍射谱积分图.图中可以观察到β-MOB2的菱面体结构的八个峰(006)、(101)、(017)、(018)、(019)、(0012)、(0110)和 (0111).衍射峰位由Multif it 4.2软件用Pseudo-Voigt函数拟合得到.此外,星号代表蜡(用于固定铍封垫)的峰,且不随压力增加而移动.

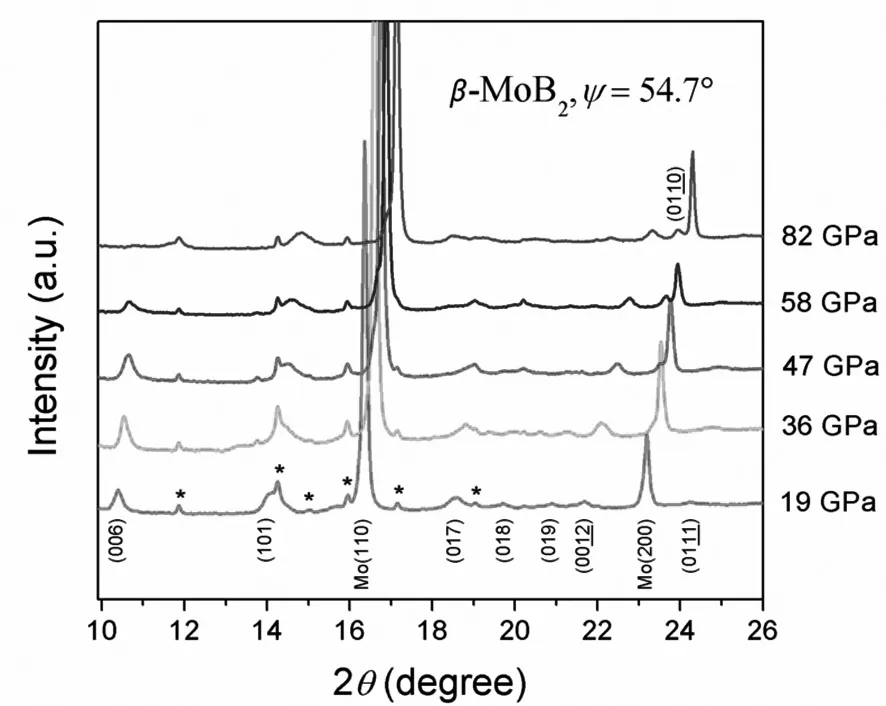
图2　β-MOB 2在y=54.7°时不同压力下的静水压衍射谱.压力由钼压标给出.星号代表蜡的峰.

不同压力下,对dm(hkl)随1-3cos2y的变化关系进行线性拟合,拟合图见图3.可以看出,拟合结果符合晶格应变理论提出的线性关系.[18,19]

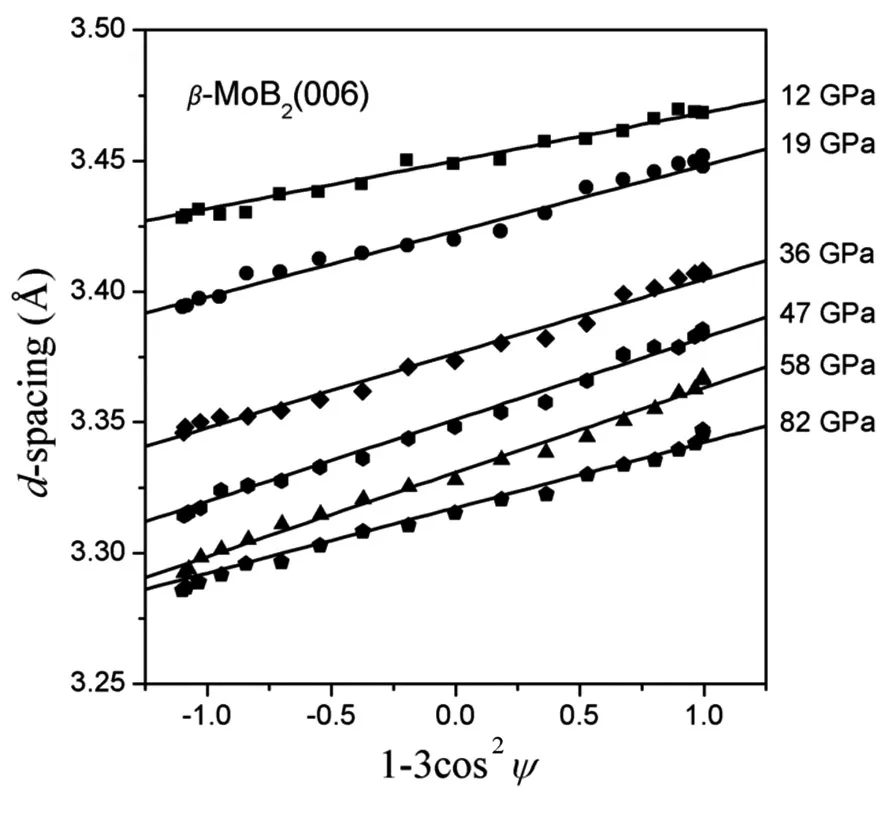
图3　d m(110)随1-3cos 2 y变化的线性拟合图

3.2　静水压下状态方程

对于角度色散X射线径向衍射实验,用ψ=54.7°时确定的dp(006)、dp(101)、dp(017)和 dp(0012)确定在静水压下β-MOB2的晶胞参数和体积.在ψ=0°、ψ=54.7°和ψ=90°时归一化的压力-体积(P-V)曲线见图4.

体积随压力的变化关系由三阶Brich-Mur naghan方程拟合,其中三阶Brich-Murnaghan方程表示为:[23]

其中K0,K0',和V0分别为体弹模量、体弹模量一阶导数和常压时的体积.ψ=54.7°时获得的体弹模量和其一阶导数分别为300(8)GPa和6.66(47).ψ=0°和90°时拟合得到的体弹模量分别是161(8)GPa和387(10)GPa.

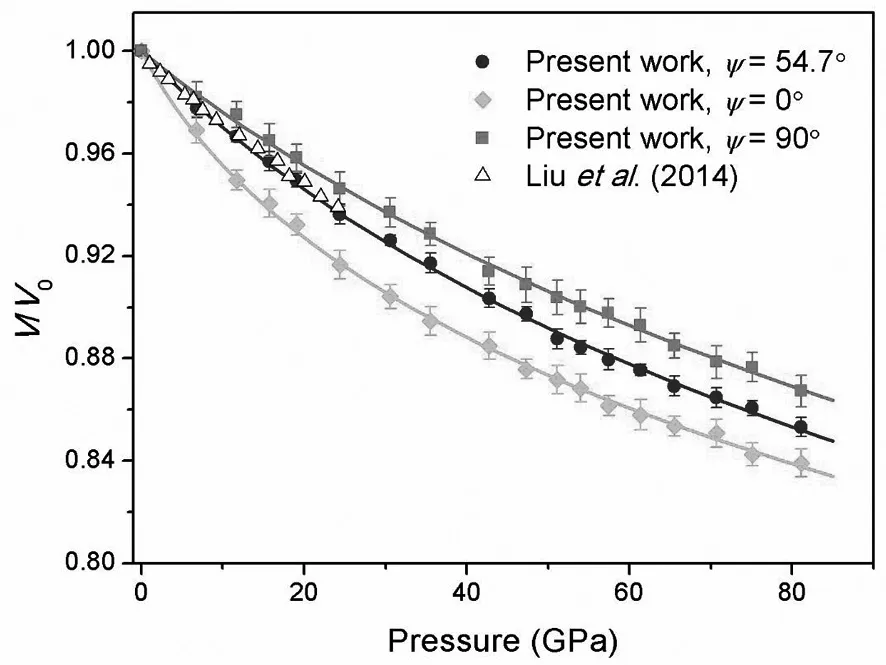
图4　ψ=0°、ψ=54.7°和ψ=90°时的P-V压缩曲线

本文β-MOB2的体弹模量和其一阶导数的拟合结果同文献值的比较见表1.[9,14-17]可以发现,本文在静水压下拟合得到的体弹模量和Tao等人的结果一致,[9,16]但是稍小于Zhang等人的理论计算结果.[14,15,17]

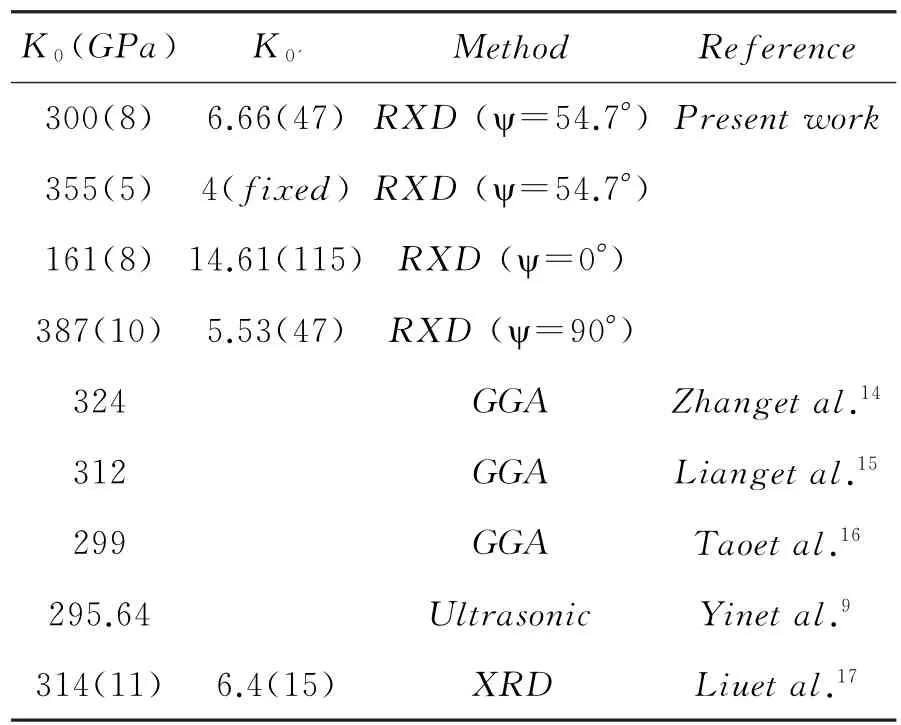
表1　β-MOB 2的体弹模量和其一阶导数同文献结果的对比.GGA表示广义梯度近似

3.3　差应力t

图5表示β-MOB2的t/G随压力的变化.在7-82 GPa的压力范围内从0.016变化到0.035.t/G在19GPa后几乎不变,表明开始由于塑性形变而发生屈服,此时的值是0.034.

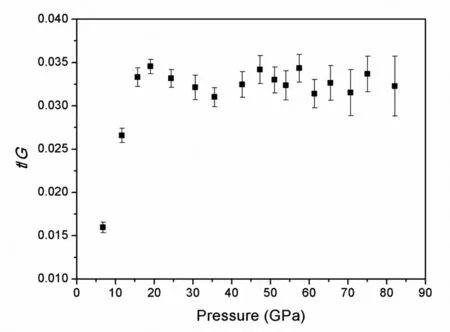
图5　t/G随压力的变化关系图

根据第一性原理计算得到的高压下的剪切模量(见图6),我们得到了每个压力点的差应力.图7比较了β-MOB2和c-BC2N,[24]B6O,[25]γ-Si3N的径向衍射实验结果.4[26]β-MOB2在75GPa时,有最大的差应力,且为11GPa.作为比较,c-BC2N在66GPa时有最大的差应力,[24]且为38GPa.B6O在65GPa时有最大的差应力,[25]且为30GPa.γ-Si3N在68GPa时有高达23GPa的差应力.可以看出,4[26]β-MOB2的差应力要远小于c-BC2N、B6O和γ-Si3N的结果.[24-26]

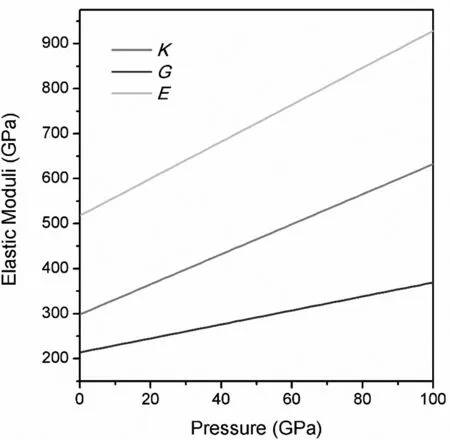
图6　高压下β-MOB 2的弹性模量

β-MOB2的差应力在超过19GPa后增加缓慢,表明此时由于塑性形变而发生屈服,此时对应的差应力是8GPa.作为比较,c-BC2N在66GPa时发生屈服,[24]对应的差应力是38GPa.B6O在65GPa时发生屈服,[25]此时的差应力时29.5GPa.γ-Si3N在35GPa时发生屈服,4[26]对应的差应力时16GPa.上述结果表明,β-MOB2的维氏硬度要小于另外三个材料的维氏硬度(c-BC2N为70 GPa,[27]B6O为45 GPa,[28]γ-Si3N4为35-43 GPa).[29-31]因此,我们认为β-MOB2不是超硬材料.

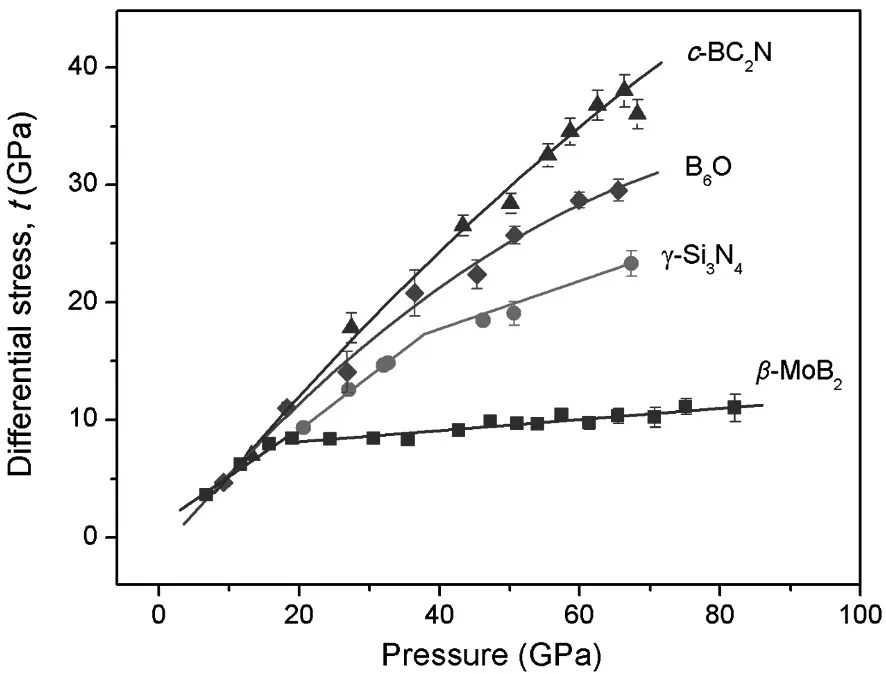
图7　β-MOB 2、c-BC 2 N、B 6O和γ-Si 3 N 4.的差应力随压力的变化图

5　结论

本文中,用径向衍射实验在非静水压下研究了β-MOB2到82GPa的强度和状态方程.径向衍射数据拟合得到的体弹模量和其一阶导数分别为300(8)GPa和6.66(47).t/G在超过19 GPa变化缓慢,表明开始发生塑性形变.根据高压下的剪切模量,当β-MOB2在19 GPa发生塑性形变时,差应力为8 GPa.β-MOB2在75GPa时有最大的差应力,且为11GPa.此外,我们认为β-MOB2不是超硬材料.

参考文献:

[1]Knappschneider A,Litterscheid C,Kurz man J,et al.Cr ystal str ucture refine ment and bonding patter ns of Cr B4:a boron-rich boride with a fr a mewor k of tetr ahedr all y coor dinated B ato ms[J].Inor ganic Che mistry,2011(50):10540-15042.

[2]Niu H Y,Wang J Q,Chen X Q,et al.Str ucture,bonding,and possible super har dness of Cr B4[J].Physical Review B,2012(85):144116-144123.

[3]Wang M,Li Y W,Cui T,et al.Origin of har dness in WB 4 and its i mplications for ReB4,Ta B4,Mo B4,Tc B4,and Os B4[J].Jour nal of Applied Physics,2008(93):101905-101907.

[4]Kaner R B,Gil man J J,Tolbert S H.Designing Super har d Materials[J].Science,2005(308):1268-1269.

[5]Cu mberland R W,Weinberger M B,Gil man JJ,et al.Rational design and characterization of inco mpressible superhar d materials[J].Journal of the American Chemical Society,2005(127):7264-7265.

[6]Chung H Y,Weinberger M B,Levine J B,et al.Synthesis of ultr a-incompressible super har d r henium diboride at a mbient pressure[J].Science,2007(316):436-439.

[7]Subramanian C,Murthy T S,Suri A K.Synthesis and consolidation of titanium diboride[J].International Journal of Refractory Metals and Hard Materials,2007(25):345-350.

[8]Gu Q F,Krauss G,Steurer W.Transition Metal Borides:Super har d versus Ultr a-incompressible[J].Advanced Materials,2008(20):3620-3626.

[9]Yin S,He DW,Xu C,et al.Har dness and elastic moduli of high pressure synthesized Mo B2and WB2compacts[J].High Pressure Research,2013(3):409-417.

[10]Frotschera M,Kleinb W,Bauerc J,et al.M2B5or M2B4?A Reinvestigation of the Mo/B and W/B System[J].Zeitschrift Für Anorganische Und Allgemeine Chemie,2007(663):2626-2630.

[11]Chen X Q,Fu C L,Krc mar M,et al.Electronic and Str uctur al Origin of Ultrainco mpressibility of 5 d Tr ansition-Metal Diborides MB2(M=W,Re,Os)[J].Physical Review Letters,2008(100):196403-196406.

[12]Wang J,Wang Y J.Mechanical and electronic properties of 5d transition metal diborides MB2(M=Re,W,Os,Ru)[J].Journal of Applied Physics,2009(105):083539-083544.

[13]Ivanovskii A L.Mechanical and electronic properties of diborides of transition 3d–5d metals from first principles:Towar d search of novel ultra-incompressible and super har d materials[J].Journal of Materials Science,2012(57):184-198.

[14]Zhang M G,Wang H,Wang H B,et al.Str uctural Modifications and Mechanical Properties of Mol ybdenum Borides from First Principles[J].Journal of Physical Chemistry C,2010(114):6722-6725.

[15]Liang Y C,Yuan X,Fu Z,et al.An unusual variation of stability and har dness in mol ybdenumborides[J].Applied Physics Letters,2012(101):181908-181912.

[16]Tao Q,Zhao X P,Chen Y L,et al.Enhanced Vickers har dness by quasi-3D boron net wor k in Mo B2[J].RSC Advances,2013(3):18317-18322.

[17]Liu P P,Peng F,Yin S,et al.Ex ploring the behavior of mol ybdenu m diboride(Mo B2):A high pressure x-r ay dif f r action study[J].Journal of Applied Physics,2014(115):163502-163505.

[18]Singh A K.The l attice str ains in a speci men(cubic system)compressed nonhydrostaticall y in an op posed anvil device[J].Jour nal of Applied Physics,1993(73):4278-4286.

[19]Singh A K,Balasingh C.The lattice str ains in a speci men(hexagonal system)compressed nonhydrostaticall y in an op posed anvil high pressure setup[J].Jour nal of Applied Physics,1994(75):4956-4962.

[20]Hixson R S,Fritz J N.Shock co mpression of tungsten and mol ybdenum[J].Journal of Applied Physics,1992(71):1721-1728.

[21]Xiong L,Liu J,Bai L G,et al.Radial x-r ay diffr action of tungsten tetr aboride to 86 GPa under nonhydrostatic co mpression[J].Journal of Applied Physics,2013(113):033507-033511.

[22]Ha mmersley A P,Svensson S O,Hanfland M,et al.Two-di mensional detector soft ware:Fr om real detector to idealised i mage or t wo-theta scan[J].High Pressure Research,1996(14):235-248.

[23]Birch F.Finite str ain isother m and velocities for single-cr ystal and pol ycr ystalline Na Cl at high pressures and 300°K[J].Jour nal of Geophysical Research,1978(83):1257-1268.

[24]Dong H N,He D W,Duff y T S.et al.Elastic moduli and strength of nanocr ystalline cubic BC2N from x-ray diffr action under nonhy drostatic co mpression[J].Physical Review B,2009(79):014105-014110.

[25]He D W,Shieh S R,Duff y T S.Equation of state and strength of boron suboxide fromradial x-ray diffr action in a dia mond cell under nonhydrostatic co mpression[J].Physical Review B,2004(70):184121-184129.

[26]Kiefer B,Shieh S R,Duff y T S,et al.Strength,el asticity,and equation of state of the nanocr ystalline cubic silicon nitrideγ-Si3N4to 68 GPa[J].Physical Review B,2005(72):014102-014111.

[27]Zhao Y,He D W,Daemen L L,et al.Super har d B–C–N materials synthesized in nanostr uctured bulks[J].Jour nal of Materials Research,2002(17):3139-3145.

[28]He D W,Zhao Y S,Daemen L,et al.Boron suboxide:As har d as cubic boron nitride[J].Applied Physics Letters,2002(1):643-645.

[29]Jiang J Z,Kragh F,Frost DJ,et al.Letter to the editor:Har dness and ther mal stability of cubic silicon nitride[J].Jour nal of Physics:Condensed Matter,2001(13):L515-L520.

[30]Tanaka I,Oba F,Sekine T,et al.Har dness of cubic silicon nitride[J].Journal of Materials Research,2002(17):731-733.

[31]Zerr A,Kempf M,Sch warz M,et al.El astic Moduli and Har dness of Cubic Silicon Nitride[J].Jour nal of the A-merican Chemical Society,2002(85):86-90.