超声载荷下TC4钛合金的疲劳寿命分析
苏胜,郭利军,张东博,高琦,王彤宇
超声载荷下TC4钛合金的疲劳寿命分析
苏胜1,郭利军2,张东博1,高琦3,王彤宇1
(1. 长春理工大学机电工程学院,吉林长春 130022;2. 凌云科技集团有限责任公司,湖北武汉 430040; 3. 中国科学院声学研究所东海研究站,上海 201815)
通过计算裂纹尖端应力强度因子及疲劳裂纹扩展速率d/d,由C. Paris模型推导出安全寿命N,由Bathias公式计算“哑铃”状钛合金试样的裂纹扩展寿命。通过理论计算和有限元分析超声疲劳“哑铃”状试样,得出应力最大位置。利用有限元仿真和实验数据分析TC4钛合金疲劳寿命。在20 kHz的超声疲劳试验中,试样的断口位置表明:TC4钛合金材料内部缺陷是试样萌生裂纹使断裂位置偏离最大应力处的主要原因。并得出疲劳裂纹萌生阶段寿命决定“哑铃”状试样的疲劳寿命。
疲劳寿命;应力强度因子;有限元;断裂力学
0 引言
随着工业技术的发展,诸多工程应用,如航空航天、铁路运输、生物医学等,其材料和构件常面临长时间、低幅载荷的重复作用,载荷次数高达千兆次,极易产生疲劳[1],造成重大的安全事故。例如:2007年,美军F-15C鹰式战斗机在做空中缠斗飞行训练时,因桁梁出现了金属疲劳问题,突然凌空解体。因此,研究超高周循环载荷作用下材料的疲劳行为和发生机理比较重要。
在临床应用中,超声手术刀具有刀口整齐、止血快、热损伤区域小、产生烟雾少、疗效好等优点,迅速成为超声外科临床介入治疗的重要手段[2]。对于频率=55 kHz的超声手术刀,工作1小时就经受了2×108次超高周振动。为了避免因超声手术刀疲劳断裂而造成的医疗事故,目前临床中采用超声手术刀使用一次即丢弃的方案。因此,开展超声手术刀疲劳特性的研究,探索超声刀疲劳寿命的评估方法,提高超声刀的抗疲劳性能[3-6],延长手术刀的使用寿命,以确保手术的安全性,具有重要的意义。
在传统的疲劳试验中,设计试样默认材料为均匀连续介质[7],主要是根据材料的曲线,运用线性累计损伤理论来估计构件的疲劳寿命,没有考虑材料缺陷(如表面划痕、金属夹杂、腐蚀坑、锻造缺陷等)造成的各种类型的裂纹。带着这种裂纹的构件,在交变载荷下,即使载荷低于材料本身的疲劳强度极限,裂纹也会很快扩展并断裂。本文以断裂力学为依据,将构件裂纹根部的材料元取出,制成光滑的疲劳试样。在超声载荷作用下进行疲劳试验,用以模拟构件受交变应力时钛合金的疲劳行为。通过研究钛合金的应力疲劳行为以及萌生裂纹时的扩展速率,计算出试样的疲劳寿命。通过裂纹尖端应力强度因子,分析裂纹扩展寿命与总寿命的关系。为提高结构件的抗疲劳性能和延长结构件的使用寿命,提供参考依据。
1 疲劳试样的制备
1.1 试验材料
试样材料是从宝鸡金属加工厂购买的TC4(Ti- 6Al-4V)合金棒材。其主要化学成分(质量分数,%)和力学性能见表1和表2。表2中,是弹性模量,σ是抗拉强度,σ是屈服强度是断面收缩率。

表1 试样的化学成分(%)

表2 材料的力学性能
1.2 试样的理论计算
在拉伸疲劳试验中,疲劳试样必须满足谐振条件。为了缩短试样长度并加速疲劳试验,试样通常设计为“哑铃”状,如图1所示。

图1 哑铃状试样



式中,E为材料的动态弹性模量。
设试样沿轴向各段的截面面积为:

为了获得最大的应力放大系数,使试样中间圆柱段的长度不为零。TC4的谐振长度、应力应变场及材料特性决定了试样的几何尺寸。
设试样满足谐振条件,通过参照文献[8]中的设计方法,用分离变量法解方程,得出当“哑铃”状试样中间设计为圆柱形时,具有较高的应力放大系数的结论,可通过解析计算获得这种试样的谐振长度。经计算得出本文使用的超声疲劳试样的几何尺寸,如表3所示。

表3 试样几何尺寸(单位:mm)
1.3 试样的仿真分析
对称的超声疲劳试样(如图1所示)两端自由,通过数值分析可以得出最大应力位于试样中间的圆柱截面,试样端部保持最大位移值,圆弧中间点最大应力处为振动位移节点,应力最大时,位移最小(如图2所示)。试样沿轴方向位的位移大小和应力值归一化后如图3所示。

图2 试样振动位移云图

图3 试样形变和应力值
一般疲劳循环在105周次以上称为高周疲劳[9],对于具有明显缺陷(如夹杂、缩孔)的材料,疲劳破坏常源于缺陷处[10]。所以,尽量选取中间为圆柱段的试样,这样即使最大缺陷不在试样中间,试样的疲劳断裂也会在接近最大应力处发生。
2 疲劳寿命分析
2.1 疲劳裂纹扩展速率估算
疲劳寿命由疲劳裂纹形成和裂纹扩展两部分决定。当疲劳裂纹起裂并扩展时,超声波在试样材料连续体中传播,而在裂纹面上反射,导致裂纹闭合效应减小,裂纹尖端的塑性区也较小[11]。本文测量得到了断口处裂纹萌生区域从初始裂纹半径()到第一扩展区半径(0),引用C. Paris模型预测超声疲劳实验条件下TC4材料的疲劳裂纹扩展速率为[12]
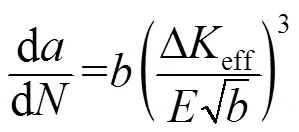

对式(4)采用Euler数值积分的方法得到TC4试样的疲劳寿命[12]:

对式(5)进行计算得出N=7.46×109,对数寿命为lgN=9.872。
2.2 疲劳寿命有限元仿真分析
采用有限元软件疲劳模块分析,设置参数为:应力比-1,20 kHz,max=330 MPa,由此得到的疲劳仿真结果如图4所示。通过数值分析获得试样在循环1.70×109周次时的对数寿命为lgN= 9.230,这与式(5)中的计算结果相接近。寿命最小处为试样中间段区域,说明此区域最先出现疲劳裂纹,最后使试样断裂。
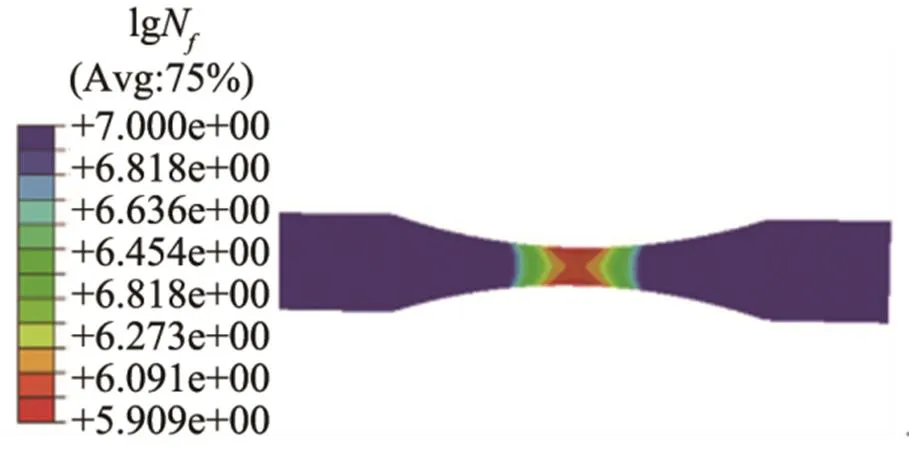
图4 试样疲劳寿命云图
3 试验及其结果分析
3.1 疲劳试验系统
如图5所示,超声疲劳试验系统由超声发生器、超声换能器、位移放大器、试样、测控系统(计算机控制系统、激光位移传感器)和冷却系统组成。

图5 超声疲劳试验系统
试验时,试件在超声波作用下发生轴向受迫振动,系统的振动频率在(20±0.5) kHz范围内,根据试样材料的基本力学性能,设置应力幅值为330 MPa,用激光测振仪探测试样表面裂纹。试验过程中试样发热,用红外热像仪测得实验过程中试样的表面温度。为避免对试验结果造成影响,冷却系统为恒温水域,控制试样温度在60℃左右。
3.2 断口分析
当试件出现疲劳裂纹时,试件谐振频率下降,系统谐振状态发生变化,试件有刺耳的声音发出,系统报警,此时记录试验循环周次及应力水平等数据,直至试样断裂再次记录。
在超高周循环下,试样的疲劳断裂更易从试件内部缺陷处开始,超声疲劳试验裂纹多数发生在试样的外表面[4]。尽管有些夹杂、缩孔等缺陷并不在试样中间最大应力处,但疲劳破坏仍会从这些缺陷处起裂。图6所示为TC4“哑铃”状试样在频率为20 kHz超声疲劳试验中发生疲劳断裂的情形,试样的疲劳破坏明显偏离试样的最大应力处。
在扫描电子显微镜下对超声疲劳试样断口进行观察,结果发现:超声疲劳试样的裂纹有内部萌生和表面萌生两种机制。图7显示了裂纹萌生时,初始裂纹形成位置一般有夹杂物。内部初始裂纹所受约束较大而且不受外部环境的影响,研究表明裂纹内部萌生疲劳极限高于裂纹表面萌生疲劳极限[13]。如图7(a)所示,材料内部疲劳裂纹附近产生二次裂纹所需的时间更久。超声负载试验中,疲劳裂纹从试样表面萌生。在下列情况下,裂纹萌生位置由表面转入内部:(1) 材料内部有尺寸较大的夹杂物缺陷;(2) 材料表层硬度远高于内部或试样表面存在残余压应力,如图7(b)所示。图8为某试样断口的形貌,图9为其细节图。由图8、9可知,在A区域产生了二次裂纹,当位错塞积形成的应力达到理论断裂强度时,滑移带在晶界上引起的应变不断增加,晶界开裂形成二次裂纹。疲劳裂纹扩展的解理面及疲劳裂纹附近的二次裂纹并没有和初始裂纹聚合在一起。在超声负载下,材料疲劳总是在应力最高、强度最弱的局部位置上形成。疲劳源常萌生于层片板条界面,TC4域团间的二次裂纹并不扩展。

图6 试样断裂后的照片

图7 试样断裂位置-1

图8 试样断裂位置-2

图9 试样断裂位置-2的细节图
本文实验过程中发现,材料裂纹萌生位置在材料内部。文献[14]表明,在超高周疲劳试验中,裂纹萌生的位置在材料内部产生。试样断裂的位置偏离应力圆柱中间最大应力处。通过对疲劳断口进行分析发现,断口处材料存在夹杂物,如图7(b)所示。因此,材料内部裂纹缺陷并不产生在试样最大应力处,但疲劳裂纹仍会从这些缺陷处产生。
3.3 试验数据分析
表4给出了本次试验的试验数据结果,在超声波金属探伤仪中,由于编号1、2的试样显示有微弱的回波,其余试样无回波,可见材料的内部缺陷降低了试样的疲劳寿命。仿真分析默认材料是均匀的连续介质,仿真分析结果与试验数据对比结果表明,试样(编号为3、4、5、6)的疲劳寿命接近于数值分析结果。

表4 TC4试样的超高周疲劳试验结果
对表4数据利用文献[15]的方法,得出应力值为330 MPa、断裂率为50%、95%、99%时试件的安全寿命分别为:
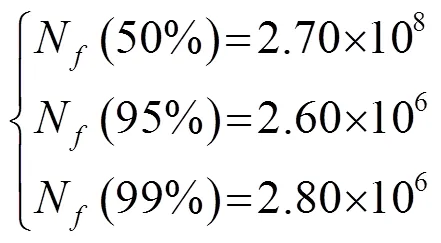
本文根据Bathias的推导,在=330 MPa应力值条件下,裂纹扩展阶段寿命N可表示为[12]


表5 TC4试样疲劳寿命试验结果比较
4 结论
本文通过数值分析计算,获得了超声疲劳“哑铃”状试样的几何尺寸及疲劳寿命,对比试验数据结果,传统的计算方法默认裂纹顶端局部疲劳应变,本文通过分析裂纹局部应变,得出如下结论:
(1) 材料内部裂纹缺陷是试样萌生疲劳裂纹使断裂位置偏离最大应力处的主要原因;
(2) TC4“哑铃”状试样的疲劳寿命主要是由疲劳裂纹萌生阶段决定,裂纹扩展寿命占安全寿命的比重很小。
[1] WANG Qingyuan, BATHIAS C, KAWAGOISHI N, et al. Effect of inclusion on subsurface crack initiation and gigacycle fatigue strength[J]. International Journal of Fatigue, 2002, 24(12): 1269- 1274.
[2] 周红生, 许小芳, 程茜, 等.超声手术刀的优化设计[J]. 声学技术, 2012, 31(5): 48-52. ZHOU Hongsheng, XU Xiaofang, CHENG Qian, et al. The optimum design of ultrasonic scalpel[J]. Technical Acoustics, 2012, 31(5): 48-52.
[3] GAO Yukui,YAO Mei,SHAO Peige. Another mechanism for fatigue strength improvement of metallic parts by shot peening[J]. J Mater Eng Perform, 2003, 12(4): 507-511.
[4] WU Yanzeng ,WANG Qingyuan, OUYANG Qianlin. Influence of subjection to plasma nitriding surface modifications on ultra-high cycle fatigue behavior of Ti-6Al-4V[J]. Applied Mechancis and Materials, 2012, 105-107(4): 1731-1735.
[5] NIKITIN A, Bathias C. Crack path in aeronautical titanium alloy under ultrasonic torsion loading[J]. Frattura ed Integrita Strutturale, 2016, 10(35): 213-222.
[6] 李庆芬. 断裂力学及其工程应用[M]. 哈尔滨: 哈尔滨工业大学出版社, 2007: 132-175. LI Qingfen. Fracture mechanics and engineering application[M]. Harbin: Harbin Institute of Technology Press, 2007: 132-175.
[7] 陈传尧. 疲劳与断裂[M]. 武汉: 华中科技大学出版社, 2008: 130-150. CHEN Chuanyao. Fatigue and fracture[M]. Wuhan: Huazhong University of Science and Technology Press, 2008: 130-150.
[8] 薛红前, 陶华, BATHIAS C. 超声疲劳试样设计[J]. 航空学报, 2004, 25(4): 425-429. XUE Hongqian, TAOHua, BATHIAS C.Ultrasonic fatigue specimen design[J]. Acta Aeronautica Et Astronautica Sinica, 2004, 25(4): 425-429.
[9] 王清远, 刘永杰. 结构金属材料超高周疲劳破坏行为[J]. 固体力学学报, 2010, 31(7): 496-503. WANG Qingyuan, LIU Yongjie. Ultra-high cycle fatigue behavior of structural metal materials[J]. Chinese Journal of Solid Mechanics, 2010, 31(7): 496-503.
[10] 中国航空研究院. 应力强度因子手册[M]. 北京: 科学出版社, 1981: 396-400. China Aviation Research Institute. Stress intensity factor manual [M]. Beijing: Science Press, 1981: 396-400.
[11] 张安哥, 朱成久. 疲劳、断裂与损伤[M]. 成都: 西南交通大学出版社, 2006: 99-107. ZHANG Ange, ZHU Chengjiu. Fatigue、fracture and damage [M]. Chengdu: Southwest Jiaotong University Press, 2006: 99-107.
[12] BATHIAS C, PARIS C. Gigacycle fatigue in mechanical practice [M]. Newyork: Marcel Dekker, 2005: 105-180.
[13] 杨王玥, 强文江. 材料力学行为[M]. 北京: 化学工业出版社, 2009: 74-127. YANG Wangyue, QIANG Wenjiang. Mechanical behavior of materials[M]. Beijing: Chemical Industry Press, 2009: 74-127.
[14] 胡燕慧, 张峥, 钟群鹏, 等. 金属材料超高周疲劳研究进展[J]. 机械强度, 2009, 31(6): 979-985. HU Yanhui, ZHANG Zheng, ZHONG Qunpeng, et al. Research progress on ultrahigh cycle fatigue of metal materials[J]. Journal of Mechanical Strength, 2009, 31(6): 979-985.
[15] 郑修麟. 金属疲劳的定量理论[M]. 西安: 西北工业大学出版, 1994: 168-200. ZHENG Xiulin. Quantitative theory of metal fatigue[M]. Xi'an: Northwest University of Technology, 1994: 168-200.
Fatigue life analysis of TC4 titanium alloy under ultrasonic loading
SU Sheng1, GUO Li-jun2, ZHANG Dong-bo1, GAO Qi3, WANG Tong-yu1
(1. School of Mechatronical Engineering Changchun University of Science and Technology, Changchun 130022, Jilin, China;2. Ling Yun Science&Technology Group CO. LTD.,Wuhan 430040,Hubei,China;3.Shanghai Acoustics Laboratory,Chinese Academy of Sciences, Shanghai 201815, China)
The position of maximum stress in the ultrasonic fatigue test of dumb-bell shaped TC4 titanium alloy specimen is determined by theoretical calculation and the finite element simulation. In the 20 kHz ultrasonic fatigue test, the fracture position of the specimen shows that the internal defect of TC4 material is the main reason of the crack initiation to make the fracture position deviated from the maximum stress position. The fatigue life of TC4 is analyzed by finite element simulation and experimental data. By calculating the stress intensity factor at crack tip and the fatigue crack growth rate, the safety lifeNis derived from the C.Paris model. The Bathias formula is used to calculate the crack propagation life of the dumb-bell shaped specimen, and the fatigue life of the specimen is determined by the crack initiation life.
fatigue life; stress intensity factor; finite element; fracture mechanics
TB553
A
1000-3630(2018)-01-0057-05
10.16300/j.cnki.1000-3630.2018.01.010
2017-11-15;
2018-01-23
国家自然科学基金项目(11474042、11774382、11574348)
苏胜(1987-), 男, 吉林长春人, 硕士, 研究方向为现代机械设计理论与方法。
王彤宇, E-mail: wty_salas@126.com

