基于质心理论的多Sink节点重选址算法*
高丽娜,戴天虹,李 昊
(东北林业大学机电工程学院,哈尔滨 150040)
如何在WSNs的监测区域内部署多个有目的、可调控的Sink节点,既可以削弱“能量空洞”问题,还可以更好的均衡网络负载,节约网络能耗,提高网络性能,是当前WSNs中一个新的研究热点。文献[1]通过分析传感器网络数据流的分布,利用启发式算法求解Sink节点的最优位置,使通过Sink节点的总数据流最大,但该算法网络总能耗过大且不适合动态网络。文献[2-4]研究移动多Sink节点选址问题,根据传感器节点数量把网络划分为若干子网络,在子网中通过最大平衡连接分区MBCP(Maximally Balanced Connected Partitio)技术,寻找Sink节点最优位置解,使分区内能耗最低,从而延长网络生命周期。文献[5-6]研究双层传感器网络Sink节点和中继节点的拓扑结构,利用迭代算法,在监测区域内找到中继节点覆盖所有传感器节点,并结合优化算法得出Sink节点的最优位置,该方法适用于异构传感器网络,但传感器节点、中继节点及Sink节点是以单跳模式相互通讯。文献[7-8]在双层异构传感器网络中,使用k-均值聚类算法(k-means clustering algorithm)寻找每簇的中心作为Sink节点的最佳位置,但该算法须已知网络中每个传感器节点的位置,一旦节点位置发生变化或节点死亡,则计算结果失效。
本文将网络中某段时间内向Sink节点发送过数据包的全部一跳邻居节点视为质点系,所发送的数据量作为质点质量,使Sink节点向着传感器节点密度大的方向移动,并配合对Sink节点移动的限制,达到多个Sink节点相互协作,逐步逼近移动到Sink节点新位置,即该质点系的质心位置,可以更好地均衡网络负载,提高数据转发成功率,延长网络生命周期。
1 质心理论
1.1 质心定义
在物理学质点系的研究中,有一个特殊的点,在质点系动力学理论中具有重要作用,称为质点系的质量中心,简称质心[9]。它的作用与质点系上的力系无关,质心是质点系质量分布的平均位置,假设质点系由N个质点组成,其中它们的质量是m1,m2,…,mN[9-11]。若用r1,r2,…,rN表示质点系中各质点相对于某一固定点O的矢径,则用rσ表示质心的矢径,即式(1):
(1)

图1 质点位置示意图
1.2 问题分析
对于多Sink节点重选址问题,我们可以将某段时间内向Sink节点发送过数据包的全部一跳邻居节点视为质点系,所发送的数据量作为质点质量,而质点系中必然就会存在质心的位置,而此时的质心位置就是Sink节点需要移动到的最优位置[12]。这样就将多Sink节点选址问题与数学和物理问题联系起来,从而更好的解决Sink节点重选址问题。通过位置矢量的直角坐标轴分量,可得质心坐标表达式,如式(2)所示,图1为质点位置示意图。
(2)
2 质心重选址算法
2.1 算法分析
假设在监测区域内,随机分布若干个传感器节点和若干个Sink节点,网络工作正常,当Sink节点j在接收数据包时,需要做以下准备工作:
Step 1 记录转发的数据邻居节点,并在接收到数据后确认;
Step 2 判断该阶段内接收的数据总量TOTALj是否够ω个;
Step 3 判断邻居节点i转发的数据量SUMi是否超过数据总量TOTALj的ρ倍;
Step 4 当Sink节点j在接收到某一个数据包后,符合Step 2和Step 3要求的前提下,启动Sink节点重选址算法;反之,Sink节点则继续正常工作。
多Sink节点重选址启动流程如图2所示。
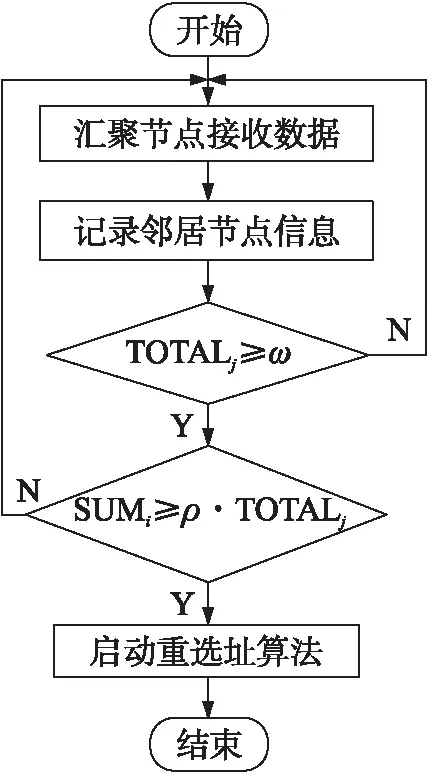
图2 Sink节点重选址启动流程图
当Sink节点j进入重选址阶段,该Sink节点首先应根据式(2)计算出此时的坐标值。在重选址算法启动前应先确定该节点坐标值与其他Sink节点的当前坐标是否相邻,避免多个Sink节点同时移向相同监测区间。若它们之间的距离小于ξ,则Sink节点j保持原地不动,反之则进行重选址。当Sink节点j确认自己可以重新选址后,则向Rt范围内的一跳邻居节点广播

图3 Sink节点重选址移动流程图
2.2 算法流程
Sink节点j移动和传感器节点i在接收指令信息时,Sink节点重选址移动流程图如图3所示。具体步骤如下:
Step 1 初始化,判断此时传感器节点i是否在汇聚节点j通信半径Rt监测区域SE内,若在该区域,且该传感器节点i向汇聚节点j转发了数据,则记录该传感器节点的位置信息;
Step 2 汇聚节点j根据式(2)更新坐标;
Step 3 判断汇聚节点j与相邻汇聚节点之间的距离dj是否大于ξ,若大于ξ,汇聚节点移动并广播
Step 4 当汇聚节点j移动到监测区域SI,判断汇聚节点j与相邻汇聚节点之间的距离dk是否大于ξ,若大于ξ,则广播
Step 5 判断传感器节点i是否接收到了
2.3 实例分析
假设试验区一个Sink节点A附近有邻居传感器节点a,b和c,初始位置如图4(a)所示,假设某段时间内,传感器节点a,b和c分别向Sink节点A发送了5个、15个、20个数据包。根据式(2)计算可得Sink节点A的新坐标如式(3)所示,且移动后位置如图4(b)所示。
(3)
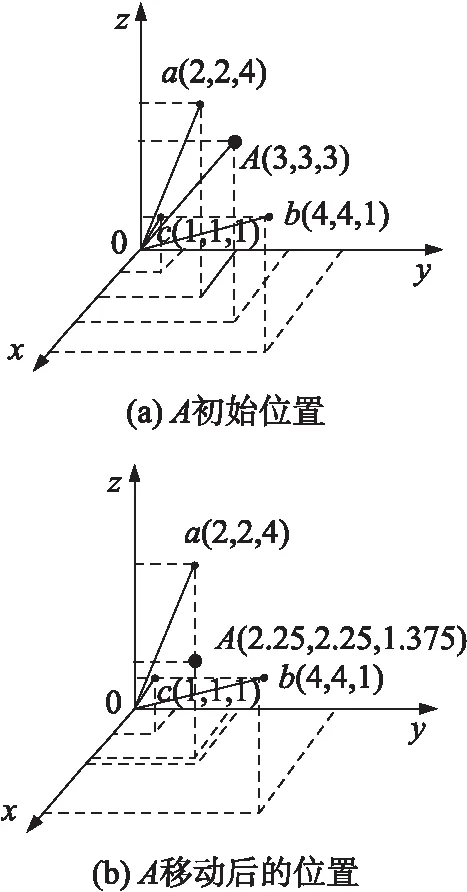
图4 Sink节点移动坐标示意图
根据式(2)计算可得Sink节点新位置,符合质心的物理学定义,在Sink节点接收数据包时满足Sink节点重选址启动条件后,在网络运行过程中逐步逼近最优位置,并不是一步到位,且该算法在移向最优位置的过程中,还兼顾了传感器节点稀疏的区域,从而有效的避免了Sink节点位置移动过快,节约传感器节点在局部重建路由上的能耗,以路由代价的提升抵消了Sink节点重选址所带来的能耗。
除此之外,该算法还考虑到了如何避免多个Sink节点同时移向相同传感器监测区域的情况,通过计算Sink节点移动后距离是否允许移动到新位置,进行有效的控制,突出了多Sink节点间可协作移动的特点。当Sink节点逐步移向传感器节点较密集的监测区域时,该区域的传感器节点以最少的跳数,将数据包传送给Sink节点,降低丢包率,该算法的合理性及高效性通过以下仿真实验进一步验证。
3 仿真实验
3.1 仿真设置
在OMNeT++[13-14]仿真平台主要针对网络生命周期、数据转发成功率两方面将基于质心的多Sink节点重选址算法与多Sink节点位置固定和基于COST函数[15]的多Sink节点重选址算法进行对比实验,从而验证质心多Sink节点重选址算法的有效性及可靠性。
为保证节点密度对实验结果的影响最小,仿真过程中随机分布传感器节点,且监测区域随节点数量作出适当的改变。仿真主要分两部分,第1种仿真环境设置传感器节点为400、600和800个,分别分布在400 m×400 m、600 m×600 m和800 m×800 m范围内,其中Sink节点数量为5。第2种仿真环境在400 m×400 m监测区域内随机分布400个传感器节点,其中Sink节点数量从1到10个依次递增,并观察Sink节点数量对WSNs性能的影响。但在仿真过程中,需对下几点进行约束:
①传感器节点和Sink节点均随机分布在监测区域内,网络运行时,所有传感器节点保持静止不动,而Sink节点则可以在监测区域内无限制移动;
②结果统计分析时,忽略Sink节点因移动所消耗的时间,当Sink节点得到要移动的新位置坐标后,可在允许范围内快速移动,不考虑移动过程消耗的时间;
③为了使Sink节点更精确地计算出重选址最优位置坐标,在网络运行期间,全部传感器节点可在需要的时候提取自己的位置坐标;
④传感器节点的发送和接收数据的能量模型采用一阶无线模型[16-17],即式(4)所示:
ETX(d)=Eelec+εampd2
ERX=Eelec
(4)
其他仿真参数设置如表1所示。
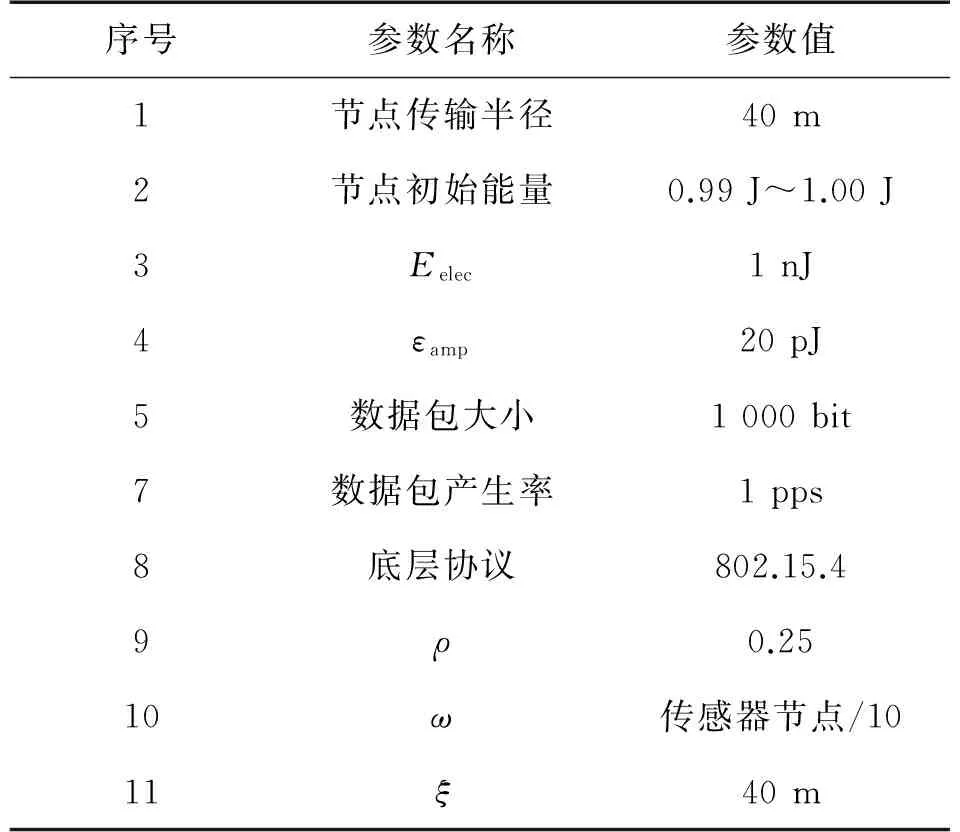
表1 仿真参数
如图5所示,为5个Sink节点、400个传感器节点随机分布在400 m×400 m监测区域内的示意图。

图5 一种节点随机分布示意图
如图6所示,为网络生命周期结束后5个Sink节点通过质心重选址算法移动后的位置示意图,此时传感器节点静止不动。

图6 Sink节点移动后位置示意图
3.2 结果分析
3.2.1 网络节点平均剩余能量
如图7所示,为3种选址算法平均剩余能量随时间变化曲线图。可知,质心重选址算法中各节点到Sink节点距离的总和低于其他两种选址算法,对应的网络能耗更少。在网络工作前100 s,3种汇聚选址算法所对应的能耗差别并不大,质心重选址算法对应的能耗相对少于其他两种选址算法;随着仿真继续100 s后有节点死亡,部分数据包被丢弃,网络能耗速度缓慢,但其中质心重选址算法耗能速度低于另外两种选址算法,可知该算法对应的传感器节点失效速度比另外两种算法慢。
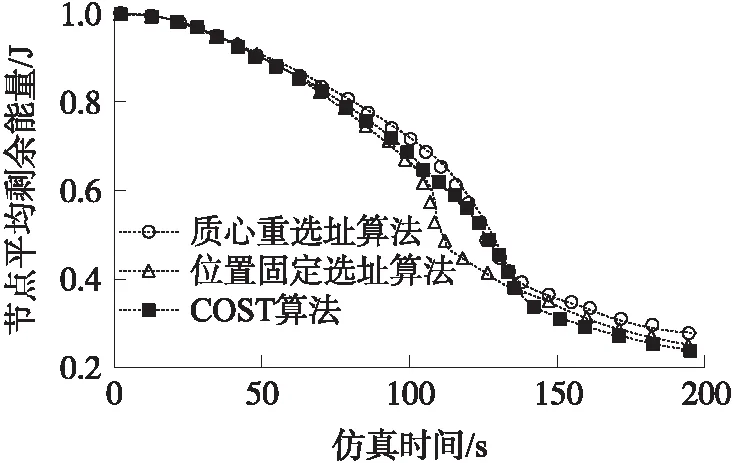
图7 网络平均剩余能量
3.2.2 数据转发平均跳数
如图8所示,节点数为400时3种算法的网络平均跳数对比图。由图可知,3种选址算法随着网络运行网络平均跳数都有所下降,但质心重选址算法对应的节点平均跳数始终低于另外两种选址算法的平均节点跳数,有效的降低了网络的丢包率提高了数据转发成功率,从而达到了延长网络生命周期的最终目的。
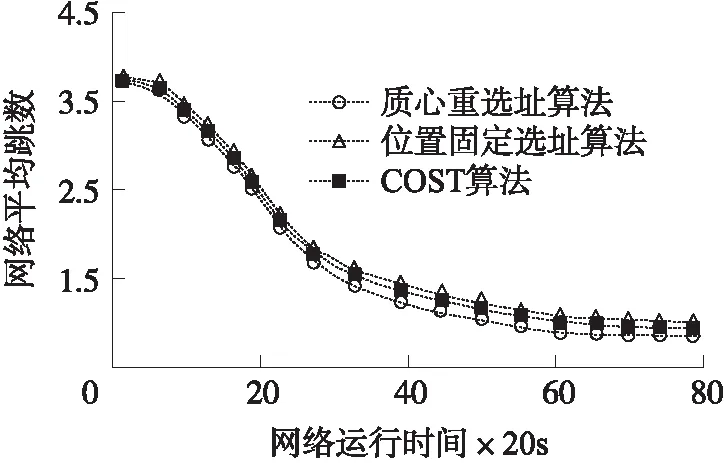
图8 节点数为400时网络平均跳数

图9 网络生命周期对比图
3.2.3 网络生命周期
如图9所示,为3种算法仿真的网络生命周期对比图。可知,质心重选址算法网络生命周期明显高于其他两种Sink节点重选址算法。由于该重选址算法使Sink节点向传感器节点密度较大的一跳邻居节点附近逐步移动,最终达到最优位置。在多Sink节点分别移向各自最优位置后,由图7、图8可知传感器节点传送数据的平均跳数和节点能耗都有效降低。并且,在多Sink节点移动过程中多个Sink节点之间是相互协作,逐步向最优位置逼近的。在此过程中,节约了传感器节点局部更新路由的能耗,进一步节约了网络能量,延长了WSNs的生命周期。而COST算法网络平均能耗大幅度增加,网络生命周期缩短,这是因为该算法需要节点全局信息,节点之间需要交换大量的数据信息。相对于位置固定选址算法,质心重选址算法和COST算法在网络生命周期方面都有所提升,质心重选址算法性能提升更加显著。
虽然在WSNs中部署多个Sink节点可以有效的均衡网络负载、降低网络能耗,但在网络工作时,若Sink节点保持不动,仍会出现邻居节点数据转发任务过重,而提早死亡,造成能量空洞,缩短网络生命周期。而多Sink节点的质点重选址算法将质心原理自适应动态调整这种变化,可以很好的适应网络环境的随时变化。
3.2.4 数据转发成功率
如图10所示,为数据转发成功率对比图。由图可知,质心重选址算法的数据包转发成功率优于其他两种算法的数据包转发成功率。因为多个Sink节点通过质心重选址算法将互相协作分别移向传感器节点密集区域,逐步逼近最优位置,缩短转发数据路径,降低丢包率。而COST算法,其数据转发成功率还低于多Sink节点固定的情况,这是因为多Sink节点固定的情况下采用的路由协议也是基于路由代价的蚁群路由算法算法,选择路由协议时考虑了路径平均最小链路质量,进行最优路径进行数据传输,从而降低网络丢包率。多Sink节点位置保持不动,邻居节点到Sink节点的跳数始终不变,数据转发成功率相对质心重选址算法低。
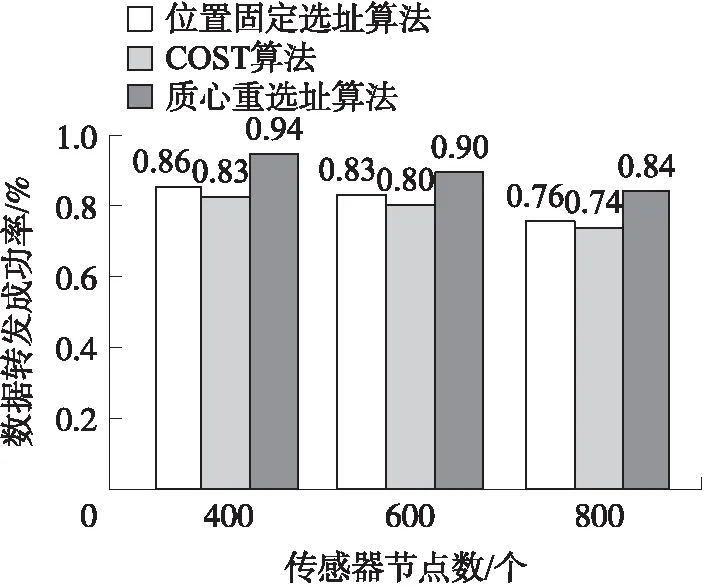
图10 数据转发成功率对比图
随着网络中传感器节点密度的增加网络中数据转发成功率不会有所提高,因为此时网络中传感器节点密度增加,所以在实际应用中,部署网络应根据实际要求部署,无需盲目高密度的部署传感器节点。
3.2.5 Sink节点数对WSNs性能影响
①网络生命周期
如图11所示,为Sink节点个数对WSNs生命周期的影响折线图,随着Sink节点个数的增加,网络生命周期呈上升趋势。此时网络中,Sink节点数量在3个~5个时最好,因为此时的网络生命周期增长速度最快,此时Sink节点个数对网络生命周期的影响最大。而但当Sink节点数目达到一定数量后,网络生命周期的增长速度缓慢,而对于其他规模的WSNs,则需进一步实验仿真验证。

图11 Sink节点数对网络生命周期的影响
②数据转发成功率
如图12所示,为Sink节点数对数据转发成功率的影响,可知,随着Sink节点数的增加网络数据转发成功率直线上升,尤其当网络中由一个汇聚节点向多个汇聚节点跳变的过程,数据转发成功率大幅度提升。对于该网络中Sink节点数量在2个~4个时最好,网络数据转发成功率最高,可见Sink节点数量的增加对数据转发成功率的影响之大。但当Sink节点个数增加大一定数目后,数据转发成功率趋于平稳,并没有很大波动,因此对于这种规模的WSNs部署3个Sink节点个数最为合理,WSNs性能最好,针对其他规模的网络,Sink节点个数应根据实际情况部署,并进行仿真实验验证。

图12 Sink节点数对数据转发成功率的影响
上述仿真实验,是在一定仿真环境假设情况下进行的,在实际应用中还需考虑很多因素,如硬件成本、环境限制、应用需求等。
4 结论
本文主要研究多Sink节点质心重选址算法,通过对质心理论的研究,将质心理论引入到多Sink节点重选址算法中,使Sink节点重选址到质心位置,并给出明确的Sink节点启动、限制移动的条件确定Sink节点重新选择的最优位置,并根据传感器节点接收信息的情况决定网络工作状态。实验结果表明,质心重选址算法不但可以避免网络出现“能量空洞”问题、均衡网络负载、降低丢包率还可延长网络生命周期。
对于多Sink节点重选址算法,忽略了Sink节点移动延迟的问题,未考虑移动中的消耗。因此在未来的实际应用中还需进一步研究,考虑当Sink节点移动延迟较大的情况,从而得到更加有效的多Sink节点重选址算法。比如,根据Sink节点不同的移动速度对重选址机制进行调整,设置Sink节点的移动速度使网络性能最优化等。
[1] Bogdanov A,Maneva E,Riesenfeld S. Power Aware Base Station Positioning for Sensor Networks[J]. Proceedings IEEE INFOCOM,2004,1:575-585.
[2] Wu D,Zhang Z,Wu W,et al. Approximation Algorithm for the Balanced 2-Connected Bipartition Problem[C]//International Computing and Combinatorics Conference. Springer International Publishing,2014:441-452.
[3] Sobti R. A Comparative Study on Network Structure Based Routing Protocol and Its Variants in Wireless Sensor Networks:A Survey[J]. International Journal of Computer Applications,2015,117(12):27-33.
[4] Slama I,Jouaber B,Zeghlache D. Multiple Mobile Sinks Deployment for Energy Efficiency in Large Scale Wireless Sensor Networks[M]//e-Business and Telecommunications. Springer Berlin Heidelberg,2008:412.
[5] Pan J,Hou Y T,Cai L,et al. Locating Base Stations for Video Sensor Networks[C]//Vehicular Technology Conference,2003. Vtc 2003-Fall. 2003 IEEE. IEEE Xplore,2003:3000-3004.Vol.5.
[6] Pan J,Cai L,Hou Y T,et al. Optimal Base Station Locations in Two Tiered Wireless Sensor Networks[J]. IEEE Transactions on Mobile Computing,2005,4(5):458-473.
[7] 王福林. 无线传感器网络中Sink节点移动策略的研究[D]. 吉林大学,2013.
[8] Oyman E I,Ersoy C. Multiple Sink Network Design Problem in Large Scale Wireless Sensor Networks[C]//IEEE International Conference on Communications. IEEE Xplore,2004:3663-3667 Vol.6.
[9] 胡嘉苇. 质心理论的应用探析[J]. 数学教学通讯(教师阅读),2011(15):48-50.
[10] 李心宏. 理论力学:Theoretical Mechanics[M]. 大连理工大学出版社,2008.
[11] 谢传锋. 动力学[M]. 北京:高等教育出版社,2004:56.
[12] 欧阳青群. 无线传感器网络能量均衡策略的研究[D]. 哈尔滨:哈尔滨工业大学,2016.
[13] Varga A. OMNeT++[M]//Modeling and Tools for Network Simulation. Springer Berlin Heidelberg,2010:35-59.
[14] Birajdar D,Solapure S. LEACH:An Energy Efficient Routing Protocol using Omnet++for Wireless Sensor Network[C]//International Conference on Inventive Communication and Computational Technologies. 2017.
[15] 刘强,毛玉明,冷甦鹏,等. 随机分布WSN中Sink节点部署研究[J]. 计算机工程与科学,2013,35(2):49-55.
[16] Friedmann L,Boukhatem L. Efficient Multi Sink Relocation in Wireless Sensor Network[C]//International Conference on NETWORK-IN Gand Services. IEEE Xplore,2007:90-90.
[17] 王宁,周圆,刘敬浩. 一种基于改进粒子群的无线传感器网络层次化聚类协议[J]. 传感技术学报,2017,30(1):120-125.

