工艺误差对盘式耦合谐振滤波器的影响*

李 豪,郑梦萍,董林玺,2*

(1.杭州电子科技大学电子信息学院,射频电路与系统教育部重点实验室,杭州 310018;2.中科院上海信息功能材料国家重点实验室,上海 200050)

现代无线通信技术的快速发展使无线电频谱资源显得相对稀缺,人类社会对于通信设备提出了更加严苛的要求。而目前,实现体积小、重量轻、易加工、成本低、品质因数高且易于集成的无源滤波器已成为当前微波技术领域的研究热点。随着MEMS技术[1]的发展,MEMS谐振器谐振频率、滤波器的运动电阻、功率处理能力等参数已经能够达到无线通信的技术要求。如:Jing Wang等人通过自对准锚加工方法实现了工作在1.156 GHz频率下的MEMS盘式谐振器,其Q值在真空和空气环境中均大于2 650[2]。John R Clark等人通过亚微米级间隙及电镀金属实现了193 MHz谐振频率及空气环境下Q值高达8880的MEMS盘式谐振器[3]。Thura Lin Naing等提出的电容式环谐振器谐振频率达到2.968 5 GHz,Q值为42 900,f×Q值高达1.27×1 014。Akgul M[4]等将盘谐振器阵列通过四分之一波长梁耦合连接实现了中心频率为223.4 MHz,带宽仅为0.09%,插入损耗为2.7 dB的带通滤波器[5]。尽管目前对MEMS谐振器、滤波器的研究比较成熟,但是对于耦合梁工艺误差对耦合谐振滤波器性能产生的影响鲜有报道。基于项目组已在忽略耦合梁倾斜效应情况下,对圆盘谐振器整体参数受工艺误差影响进行了分析,因此本文主要研究工艺误差造成的耦合梁倾斜效应对双圆盘耦合MEMS谐振滤波器中心频率及3 dB带宽的影响,并提出一种半高耦合梁设计模式。

1 理论与设计

1.1 径向模式单圆盘谐振器

电容式圆盘谐振器近年来作为一种新型的MEMS器件,其优点在于能够达到较高的谐振频率和品质因数。

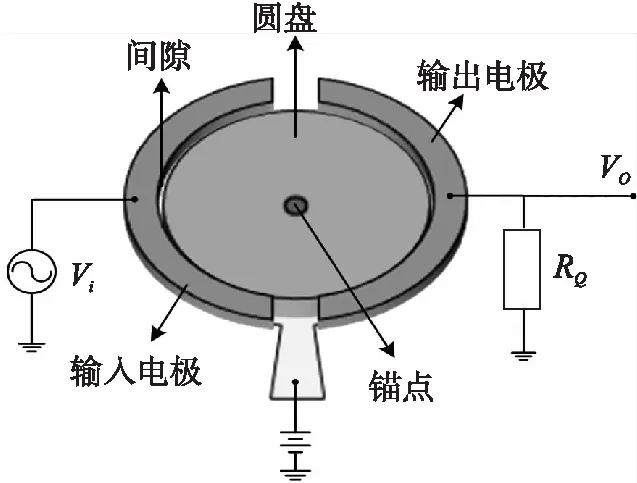
图1 圆盘谐振器示意图

如图1所示,通过将圆盘谐振频率f0处的正弦小信号电压vi施加到输入电极,并通过锚向圆盘施加直流偏置电压Vp,从而在盘上产生随时间变化的径向静电力使圆盘产生径向谐振运动。由于圆盘在整个侧面上均匀地膨胀和收缩,随着时间的变化,圆盘与输出电极间电容发生变化,因此在输出端口连接的负载中产生频率为f0的正弦运动电流i0。圆盘谐振器的谐振频率可以通过以下方程[6]得出:

(1)

式中:

(2)

式中:ω0为纯机械系统的谐振角频率,Jn为第1类n阶贝塞尔函数,R为圆盘的半径,E,ρ和σ分别为材料的杨氏模量,质量密度和泊松比。对于多晶硅,E=160 GPa,ρ=2 300 kg/m3,σ=0.22。通过对式(1)和式(2)的简化可以得出第i阶模式下谐振频率的表达式:

(3)

式中:k是与泊松比有关的常数(对于多晶硅,k为0.34 MHz/μm),αi为第i阶模态比例因子(α1=1,α2=2.64,α3=4.21)。

圆盘谐振器可以由具有单自由度的质量弹簧阻尼系统的机械模型(图2(a))表示。尽管其为机械结构,但是当从谐振器一个端口看进去时,它仍然是一个电子元件。因此可以由图2(b)中所示的电感-电容-电阻器(L-C-R)等效电路来建模。L-C-R等效电路中各元件参数的表达式采用以下形式:

(4)

式中:mre,kre和bm分别为谐振器的动态质量,机械刚度和阻尼系数。对于径向模式圆盘谐振器,其圆盘侧壁上的所有点移动相同的量,等效质量可以通过将总动能除以圆盘边界处速度平方的一半来获得[7]:

(5)

式中:t为圆盘厚度,h是由圆盘材料的杨氏模量E,密度ρ,泊松比σ和谐振角频率ω0定义的常数:

(6)

通过得到的有效质量mre可得到机械刚度kre和阻尼系数bm,其表达式如下:

(7)

(8)

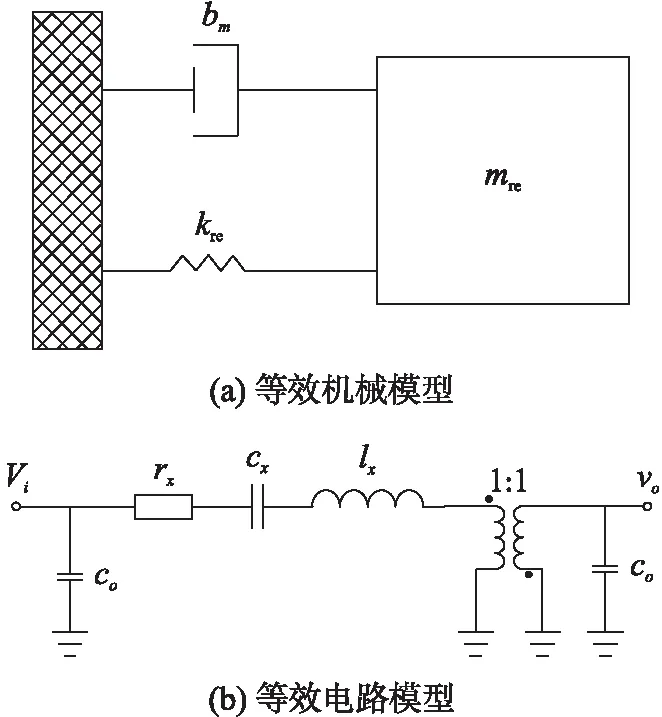
图2 圆盘谐振器等效模型

1.2 双圆盘耦合谐振滤波器

关于圆盘机械滤波器,Mehmet Akgul,Zeying Ren及Clark T C Nguyen等人已经在论文[5,8]中做了比较详细的研究。本文基于他们的研究基础之上进一步分析耦合梁倾斜对谐振滤波器相关性能的影响。为了使得研究更具针对性和准确性,我们选择了双圆盘耦合谐振滤波器,而暂不考虑多谐振器情况。

如图3 所示,对于实际的圆盘耦合谐振滤波器,由于Radial-Contour模式圆盘谐振器的振动是径向方向振动的,所以需要一个同样以伸张模式振动的耦合器。而伸张振动模式下的耦合梁符合以上要求。

图3 采用耦合梁连接的理想双圆盘滤波器(Ls=λ/4)

1.2.1 伸张模式耦合梁模型

伸张振动模式下的耦合梁特性类似于电路中的传输线,可等效成电路模型,如图4所示。

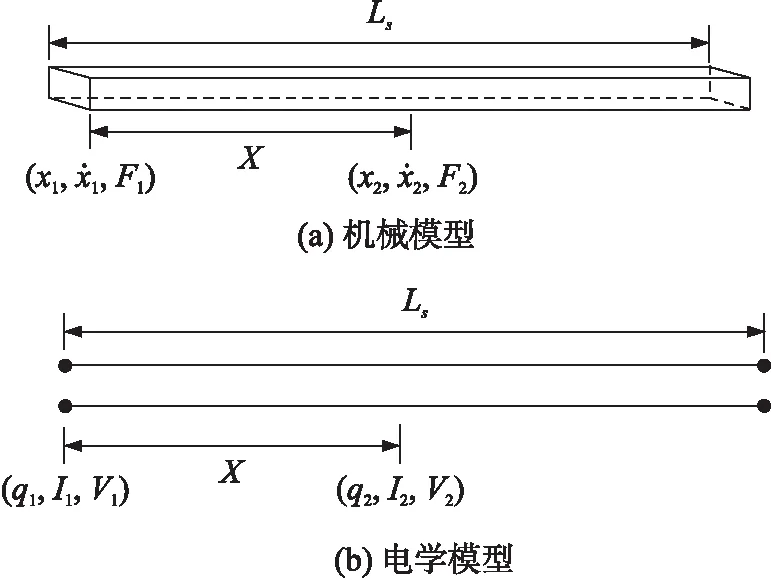
图4 传输线模型

由此,伸张振动模式下的耦合梁可以通过以下传输矩阵(ABCD)方程[9]进行描述:

(9)

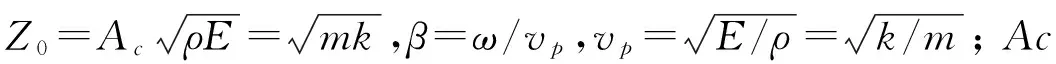
图5 耦合梁模型

为了使其可以实现电路仿真功能,可将传输矩阵方程(9)通过以下公式转换成如图5(a)中的T型Z参数网络[10]:

(10)

(11)

(12)

这样,在电路建模中可以根据Za,Zb,Zc的取值,然后将其等效成对应的电容或电感来实现最终的电路仿真。

(13)

图7耦合梁模型

1.2.2 边缘倾斜的耦合梁模型

在MEMS阵列耦合谐振器中,耦合梁质心的偏移往往是因为耦合梁尺寸的偏差引起的,例如用深反应离子刻蚀工艺(DRIE)[11-12],实际的梁常常存在倾斜效应如图6[13-14]所示。梁的截面积会随其倾角变化而发生改变,从而使得其截面如同一个梯形。因此,对于本论文所研究的耦合梁质心偏移情形,主要采用图7(a)中所示的梯形梁进行等效建模。

图6 非平行叉指的SEM图

耦合梁的截面积转换成与倾角相关的函数为:

Ac=Wc*H+H2*tanθ

(14)

式中:Wc为设计梁宽,H为梁高与圆盘厚度t相等,θ为倾斜角。

1.2.3 双圆盘耦合谐振滤波器工作原理

如图3所示,耦合谐振滤波器中两个盘谐振器的尺寸结构相一致,其各物理参数详细情况如表1所示。

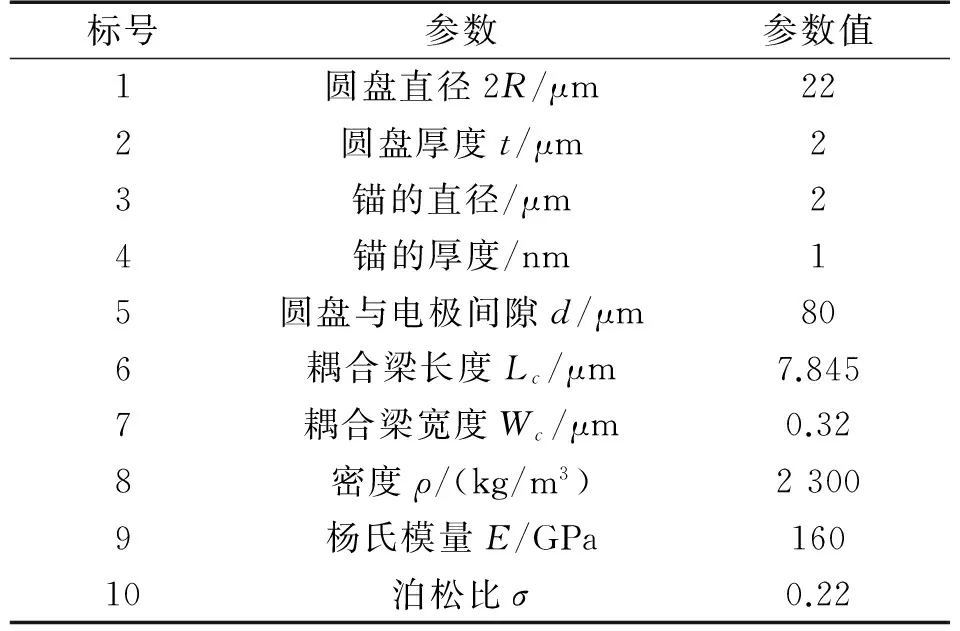
表1 滤波器设计参数

对于实际的圆盘耦合滤波器,为了使其能够实现滤波功能,必须调节耦合梁的尺寸以使其长度等于λ/4,即βLs=π/2,其中λ为谐振器工作频率所对应波长。因此,四分之一波长耦合梁的传输矩阵为:

(15)

梁长Ls为:

(16)

同时可得:

Za=jZo,Zb=jZo,Zc=-jZo

(17)

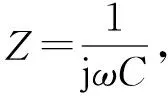
Ca=Cb=-Cc

(18)

(19)

耦合谐振滤波器的两个盘谐振器在所有方面都是相同的,它们具有相同的谐振频率。从机械角度看,两个谐振器的机械耦合产生两个自由度的机械系统,其有效地将两个谐振器相同的原始谐振频率分裂成两个模式频率,即本征状态,定义为滤波器响应的通带[15]。两个模式可以被分别表示为反相和同相模式,其中反相指两个谐振器以相反相位振动,即一个扩展,而另一个在给定时刻收缩,如图8(a)所示。而同相表示两个谐振器以相同相位振动,即两者一致地膨胀和收缩,如图8(b)所示。

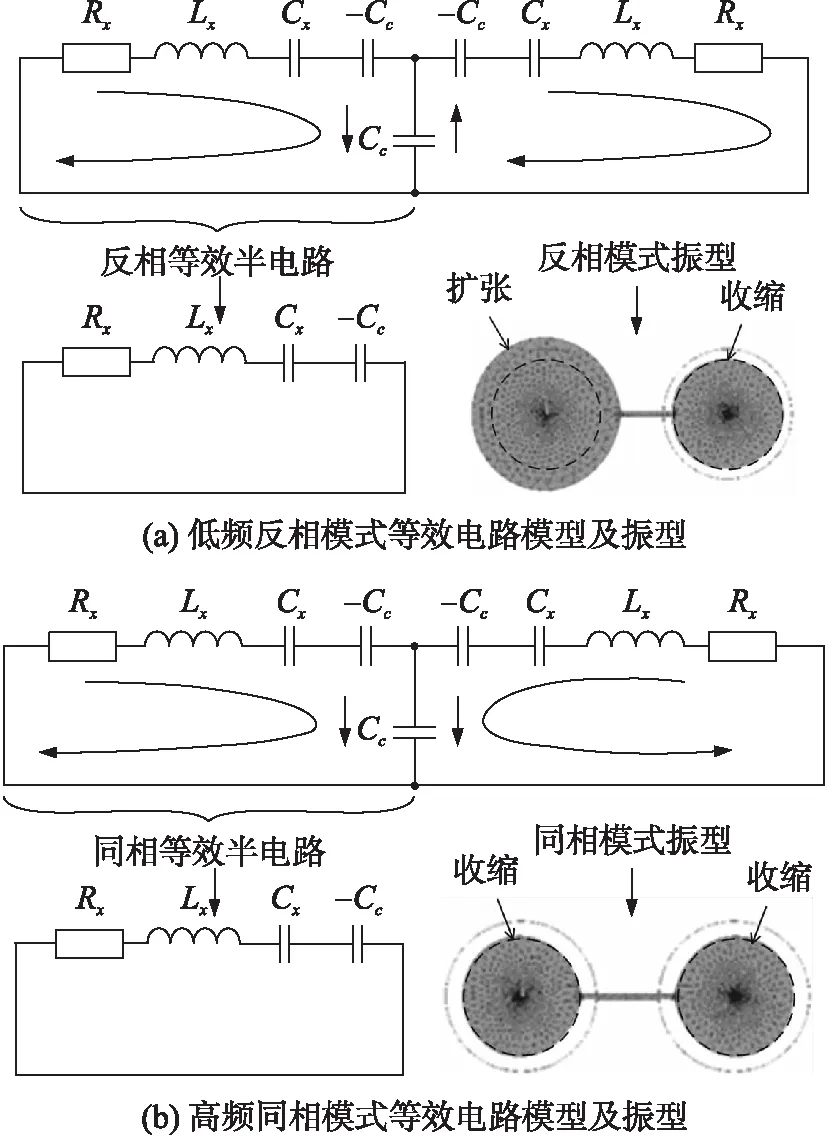
图9 等效电路模型及振型

图8 ANSYS模态仿真的双圆盘系统的径向振动模式图

图9通过该系统的等效电路来描述四分之一波长耦合梁分裂频率的机制。这里,L-C-R电路等效成每个盘式谐振器,而电容器的T网络等效四分之一波长耦合梁,基本上将其作为声传输线处理。L-C-R电路中的Lx,Cx和Rx的值由实际振动的质量,刚度和阻尼的值导出[16]。

在图9(a)中描述的低频反相模式中,耦合梁不经受应变,因为相邻的盘边缘在相反的径向方向上移位。这意味着谐振时最左(输入)盘的电流由式(20)给出:

ix=vi/Rx

(20)

ix为正的,并且流入最右(输出)盘的电流为负,即电流从盘流出到输出电极。因此,电流从输入流到输出。这意味着在电等效电路中表示为ix1和ix2的运动电流在围绕它们各自网络的顺时针方向上流动。因此它们在并联电容器Cc中抵消,这意味着耦合梁T型网络的分流臂的电压降等于零。然后这产生了图9(a)[17]所示的系统的半电路,其中值为-Cc(负电容)[18]的电容与机械谐振器的运动电容Cx相串联,从而将频率从原始谐振频率降低到较低模式频率fL,其值由式(21)给出:

(21)

在高频同相模式中,两个盘一致振动,耦合梁经受应变。这增加了系统的刚度,使其频率超过原始谐振器的频率。从等效电路的角度看,每个谐振器槽中的运动电流ix1和ix2现在围绕它们各自的网孔以相反的方向流动,这意味着它们添加在T网络的分流Cc臂中。每个网络因此吸收分流Cc的一半以产生图9(b)[17]所示的系统的半电路,其中值为+Cc的电容与运动电容Cx串联。这将网络频率提高到fH,其值由式(22)给出:

(22)

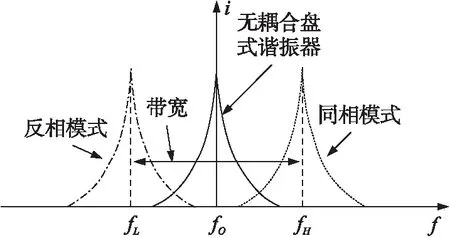
图10 无耦合盘式谐振器及低频高频滤波模式下电流频谱示意图

对于四分之一波长耦合,滤波器的中心频率等于其构成谐振器的频率,并且其3 dB带宽比由耦合模式峰分离提供的带宽Bsep(图10所示)大一点。由式(21)和(22),采取模式峰分离形式得到:

(23)

式中:cx与cc分别为谐振器机械刚度kre和耦合梁刚度kc的倒数[16]。由于滤波器带宽通常被定义为 3 dB 带宽,将修正因子kij应用于式(23)产生更常见的形式[15]:

(24)

式中:B为3 dB带宽,kij是指机械耦合滤波器中第i和第j个谐振器之间的耦合梁所需的修正因子。kij值可在滤波器相关教材[19]中查询,表2列出几个切比雪夫型滤波器kij参数。

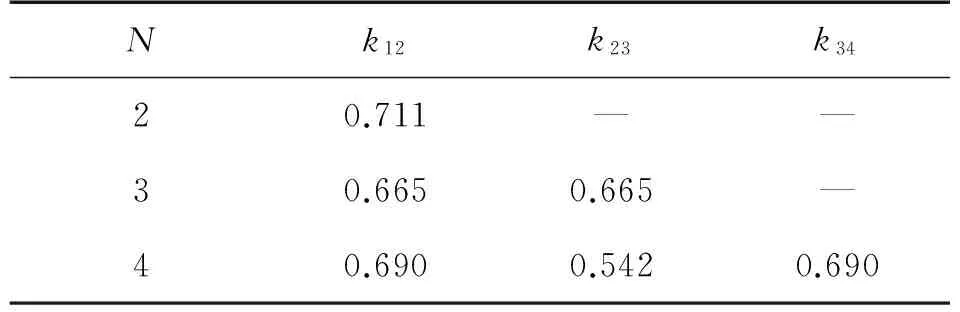
表2 kij参数值

1.3 中心半高耦合梁双圆盘谐振滤波器

通常情况下,出于工艺流程简单化,耦合梁与圆盘一体化设计(耦合梁高度与圆盘厚度一致)如1.2节设计所示。但在一些要实现高选频特性情况下需要极小的耦合梁宽度,使得耦合梁具有极大的深宽比。当耦合梁发生倾斜时由式(14)、式(24)可得:

(25)

(26)

式中:ΔB为滤波器带宽变化量,ΔB/B为带宽变化率,H为耦合梁高度,根据式(26)可知在倾斜角不变情况下,滤波器带宽变化率将与梁高与梁宽比值成正比,这将导致倾斜效应对滤波器带宽的影响随着耦合梁深宽比增大而变大,因此减小耦合梁的深宽比(增大耦合梁宽度或减小耦合梁厚度)对提高双圆盘机械滤波器抵抗倾斜效应干扰能力具有十分显著的效果。

减小耦合梁的深宽比可以从以下3个方面达到:

方案1减小谐振滤波器整体设计厚度。方案2减小谐振滤波器整体设计厚度、增大耦合梁宽度。方案3耦合梁截面积不变,仅减小耦合梁厚度、增大耦合梁宽度而不改变谐振圆盘厚度。因此本文分别仿真分析了以上3种措施对谐振滤波器稳定性的影响。

图11 不同类型耦合梁双圆盘机械滤波器简易模型

如图11所示,图11(a)为常规耦合梁机械滤波器简易模型,其梁高与圆盘厚度相同。图11(b)为中心半高耦合梁机械滤波器简易模型,其梁高度为t/2是常规型一半,梁宽为2Wc是常规型2倍,耦合位置为圆盘垂直方向中心处。图11(c)为谐振滤波器整体厚度减小为设计厚度的二分之一。图11(d)为谐振滤波器整体厚度减小为设计厚度的二分之一,梁宽增大为2Wc。

根据式(26)理论推导可知忽略中心频率微小变化情况下,半高型耦合梁双圆盘机械滤波器对倾斜效应的抗干扰性4倍优于常规型耦合梁机械滤波器。下一节通过ANSYS仿真分析来验证结论。

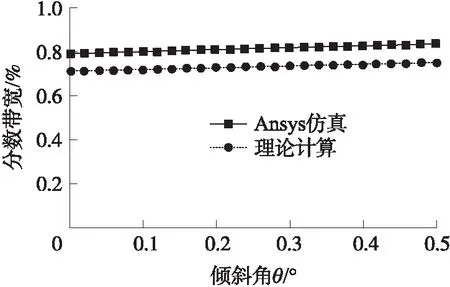
图12 耦合梁倾斜对滤波器分数带宽影响图

2 仿真分析

如图12所示,两条曲线分别为ANSYS仿真结果和电路集总参数计算结果,由于式(3)理论计算得到的频率f0与ANSYS仿真得出的频率之间存在一定的偏差,后续计算忽略了频率的变化,导致两条曲线之间存在一定的偏差。就耦合梁倾斜角大小变化而言,两曲线最明显的共同之处就是其一致的趋势,即当耦合梁倾斜角度越大,滤波器分数带宽上偏越大。仿真结果显示,当倾角达到0.5°时,分数带宽偏差将达到5.6%。

由于耦合梁尺寸的改变,机械滤波结构的整体几何形状也将受到影响。而构成滤波结构的谐振器谐振频率的大小与其结构的几何形状有着密切的关系。所以,我们通过ANSYS仿真得到了滤波器在不同耦合梁倾斜角下的中心频率变化结果。

如图13所示,当耦合梁倾斜角度变大(质心下移)时,滤波器的中心频率均会呈现下降趋势。通过进一步分析,我们发现,当倾角达到0.2°时,中心频率偏移将达到-24×10-6。当倾角在0.5°以内时,滤波器中心频率虽然会出现上下浮动,不过最大偏差在-51×10-6以内。对于这样的偏差,根据Mehmet Akgul 等人的研究,是可以通过电气刚度调谐的方式来纠正的[8]。

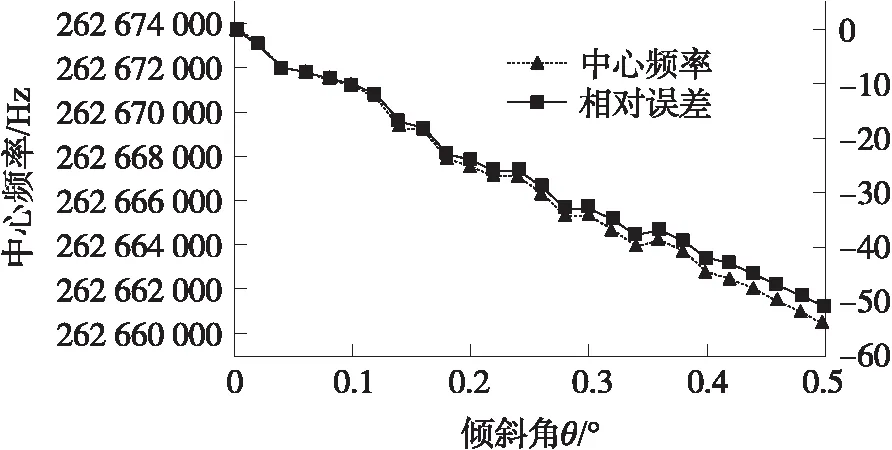
图13 耦合梁倾斜对滤波器中心频率影响图

如图14所示,方案 2(如图11(d)所示)措施对滤波器本身带宽影响过大,因此不能采用该措施来提高滤波器稳定性。所以下面进一步仿真分析方案1(如图11(c)所示)、方案3(如图11(b)所示)在倾斜角达到0.5°情况下对谐振滤波器稳定性的影响。

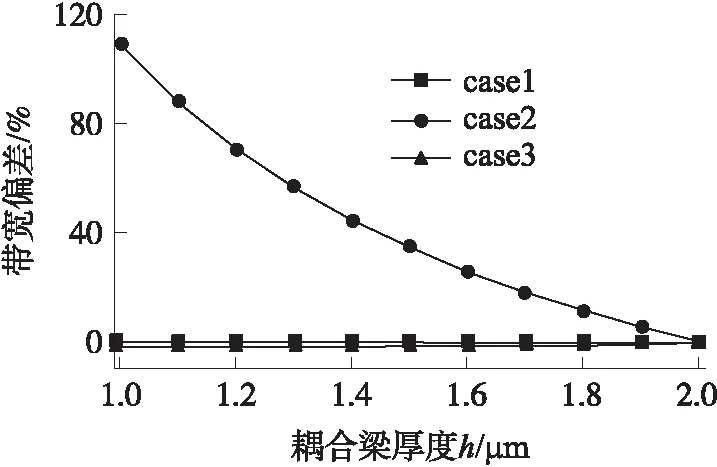
图14 不同措施对滤波器带宽影响图

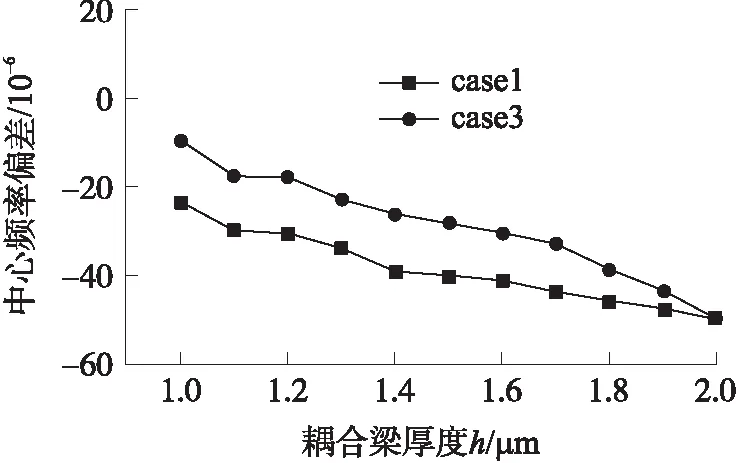
图15 0.5°倾角下方案1、方案3对谐振滤波器中心频率的影响

方案3在耦合梁截面积不变的情况下,改变梁厚以及梁宽。如图15、图16曲线所示在0.5倾角下,方案3对谐振滤波器稳定性的影响要近乎2x优于方案1。因此进一步分析方案3中半高模型对谐振滤波器稳定性的影响。

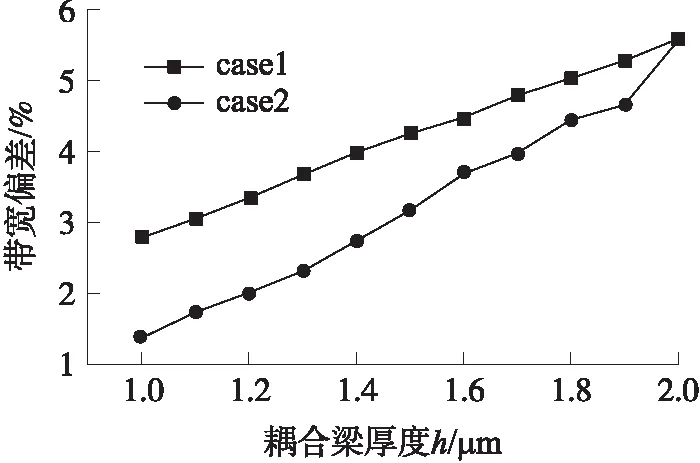
图16 0.5°倾角下方案1、方案3对谐振滤波器带宽的影响

最后通过ANSYS对半高型耦合梁滤波器模型仿真分析,对比结果如图17和图18所示。结果表明采用半高耦合梁设计滤波器时,当耦合梁分别发生0.1°、0.2°、0.5°偏移时,滤波器中心频率分别下偏1.9×10-6、2.8×10-6、9.5×10-6。同时当倾斜角达到0.5°时,分数带宽偏差仅为1.4%。与2.3节设计的常规耦合梁滤波器相比,在相同倾角下半高型耦合梁滤波器中心频率偏移及分数带宽偏差约为常规型的四分之一,与理论结果相符。

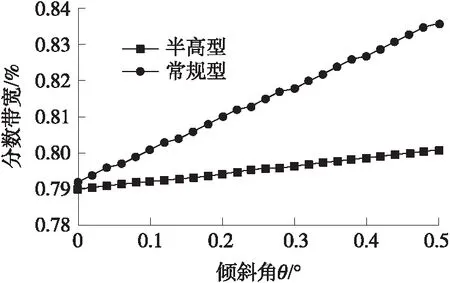
图17 不同模型耦合梁倾斜对滤波器分数带宽影响图

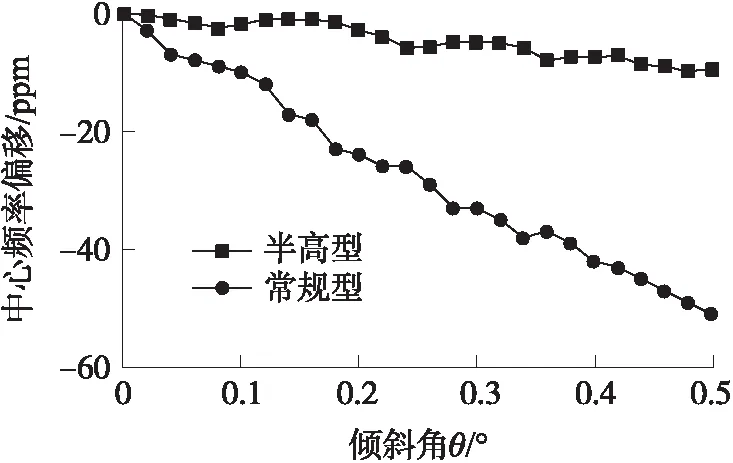
图18 不同模型耦合梁倾斜下滤波器中心频率偏移图

3 总结与展望

本文研究了阵列耦合谐振滤波器中,由倾斜效应导致的耦合梁质心偏移对耦合谐振滤波器的影响。提出了半高耦合梁模型并对相关特性进行分析对比。结果表明随着耦合梁倾斜角增大,滤波器中心频率呈波动下降,而分数带宽随之线性增大,如当耦合梁分别发生0.1°、0.2°、0.5°偏移时,滤波器中心频率分别下偏10×10-6、24×10-6、51×10-6。当倾斜角达到0.5°时,分数带宽偏差将达到5.6%。此外,采用半高耦合梁设计滤波器时,当耦合梁分别发生0.1°、0.2°、0.5°偏移时,滤波器中心频率下偏分别降低到1.9×10-6、3.8×10-6、9.5×10-6。当倾斜角在0.5°时,分数带宽偏差仅为1.4%。结果表明基于半高耦合梁设计的滤波器性能受工艺误差导致的倾斜效应方面影响要明显小于常规设计方式,该设计虽然增加了工艺复杂性,但是对于要求高稳定性的高频窄带滤波器应用场合,该方案可为MEMS滤波器结构设计提供参考。

[1] 李建华,徐立新,陈和峰,等. 基于MEMS技术的新型太赫兹混频器设计与制作[J]. 传感技术学报,2015(1):9-12.

[2] Wang J,Ren Z,Nguyen C T. 1.156-GHz self-aligned vibrating micromechanical disk resonator[J]. Ultrasonics Ferroelectrics and Frequency Control IEEE Transactions on,2004,51(12):1607.

[3] Clark J R,Hsu W T,Abdelmoneum M A,et al. High-QUHF Micromechanical Radial-Contour Mode Disk Resonators[J]. Journal of Microelectromechanical Systems,2005,14(6):1298-1310.

[4] Naing T L,Beyazoglu T,Wu L,et al. 2.97-GHz CVD Diamond Ring Resonator with Q>40,000[C]//Frequency Control Symposium. IEEE,2012:1-6.

[5] Akgul M,Nguyen T C. A Passband-Corrected High Rejection Channel-Select Micromechanical Disk Filter[C]//IEEE International Frequency Control Symposium. IEEE,2014:1-6.

[6] Basu J,Bhattacharyya T K. Comparative Analysis of a Variety of High-QCapacitively Transduced Bulk-Mode Microelectromechanical Resonator Geometries[J]. Micro-System Technologies,2011,17(8):1361-1371.

[7] 俞权. 盘结构电容式MEMS谐振器相关性能研究[D]. 杭州电子科技大学,2015.

[8] Akgul M,Ren Z,Nguyen T C. Voltage-Controlled Tuning to Optimize MEMS Resonator Array-Composite Output Power[J]. 2011:1-6.

[9] Burgess J. Mechanical Filters in Electronics[J]. IEEE Transactions on Acoustics Speech and Signal Processing,1984,32(1):191-191.

[10] Johnson R A. Mechanical Filters in Electronics[J]. Wiley,1983.

[11] Misri I,Hareesh P,Yang S,et al. Microfabrication of Bulk PZT Transducers by Dry Film Photolithography and Micro Powder Blasting[J]. Journal of Micromechanics and Micro-Engineering,2012,22(22):85017-85026(10).

[12] Hareesh P,Misri I,Yang S,et al. Transverse Inter-Digitated Electrode Actuation of Homogeneous Bulk PZT[J]. Journal of Microelectromechanical Systems,2012,21(6):1513-1518.

[13] Zuo-Yang Zhong,Wen-Ming Zhang,Guang Meng,et al. Inclination Effects on the Frequency Tuning of Comb-Driven Resonators[J]. Journal of Microelectro-Mechanical Systenms,2013,22(4):865-875.

[14] Tay F E H,Jun X,Liang Y C,et al. The Effects of Non-Parallel Plates in a Differential Capacitive Micro-Accelerometer[J]. Journal of Micromechanics and Microengineering,1999,9(4):283-293.

[15] Basu J,Bhattacharyya T K,Chaudhuri R R,et al. A Microelectromechanical Disk Resonator-Based Bandpass Filter for Wireless RF Applications[C]//Applied Electro-Magnetics Conference. IEEE,2011:1-4.

[16] Wang K,Nguyen T C. High-Order Medium Frequency Micromechanical Electronic Filters[J]. Journal of Micro-Electromechanical Systems,2002,8(4):534-556.

[17] Akgul M. A Micromechanical RF Channelizer[J]. Dissertations and Theses-Gradworks,2014.

[18] Akgul M,Wu L,Ren Z,et al. A Negative-Capacitance Equivalent Circuit Model for Parallel-Plate Capacitive-Gap-Transduced Micromechanical Resonators[J]. IEEE Transactions on Ultrasonics Ferroelectrics and Frequency Control,2014,61(5):849-869.

[19] Zverev A I. Handbook of Filter Synthesis[J]. Wiley & Sons,1967.