基于CFD的风帆助航船阻力特性研究
李冬琴, 李 季,郑 鑫,李国焕,戴晶晶
(1.江苏科技大学 船舶与海洋工程学院, 镇江 212003) (2. 江苏现代造船技术有限公司, 镇江 212003)
近年来,随着能源与环保问题的日益突出,人们对船舶的节能研究也越来越重视.利用风帆来辅助船舶航行,成为新能源应用于船舶运输中的典型方式.阻力特性是船舶的重要性能之一,因此对于船舶阻力的预报一直是人们研究的重点课题.其预报方法主要有两种:一种是通过船模试验的方法预报船舶阻力;另一种是通过计算流体力学CFD(computational fluid dynamics)的方法模拟计算船舶阻力[1-2].但船模试验的方法成本较高,且试验过程中会受到很多环境因素的限制而影响试验结果.随着计算机等相关技术的发展,计算流体力学也得到了飞速发展,并且计算效率和精度也越来越高,因此得到了广泛的应用.
对于风帆助航船来说,影响其阻力性能的因素很多,包括帆型的选择[3-4]、风帆的布置、风帆转角与风向的配合[5-7]、运动产生的漂角[8]等.但研究多以风帆的优化展开,而对于风帆与风向的配合、漂角的影响等研究相对较少.文中以4.5万吨散货船为模型,主要对风帆与风向的配合、漂角的影响进行数值模拟研究,并对结果进行分析总结,为今后风帆助航船的研究提供参考.
1 风帆的受力及模拟结果分析
1.1 受力分析
历史上,风帆结构形式多样,主要有矩形帆、三角帆、圆弧形帆、翼型帆、椭圆弧型帆等[9].通过与之前文献记载数据的比较[3,10]及数值模拟结果的分析,发现椭圆弧型风帆具有较为优秀的空气动力特性,且左右对称,对左右两个方向的来风均能产生相同的升力效果,结构形式也相对简单.因此,文中选择椭圆弧型风帆进行研究.
首先建立受力模型,如图1.图中帆翼弦的方向与表观风速方向的夹角为α,即几何攻角.翼弦线与船舶航向的夹角为θ,即帆位角.表观风向与船舶航行方向的夹角为β,即表观风向角.而真实风向与船舶航行方向的夹角为η,即为真实风向角.空气动力被分解为升力FL、阻力FD两个分力,分别沿图中方向L、D[11].其中表观风是真实风与由船速产生的风通过三角形法合成的风,如图2.对于方向有以下规定:
(1) 风向角:船顺风为0,顺时针转动为正;

图1 风帆受力
(2) 几何攻角:假定风向与帆向平行时角度为0,风向不变、顺时针转动帆则夹角为正;
(3) 帆位角:规定翼弦与航向平行为0,航向不变,风帆顺时针转动所得角度为正,反之为负.

图2 表观风速的矢量合成
对应的升力和阻力的空气动力系数:
(1)
式中:CL为升力系数;CD为阻力系数;ρ为空气密度;V为风速;S为风帆的特征面积.
1.2 数值模拟分析
由于文中研究的椭圆弧型风帆缺乏试验数据,因此选取常规翼型RAE2822为验证翼型,利用软件STAR CCM+的重叠网格技术对其进行数值模拟.选取马赫数Ma为0.725,迎角为2.92°,雷诺数Re为6.5×106.图3、4、5分别为翼型的网格、压力分布、及升阻力系数曲线,n为迭代次数.

图3 翼型帆的网格

图4 压力分布

图5 升阻力系数曲线
将模拟所得的翼型气动特性参数与试验参数进行对比,如表1,模拟误差较小,验证了数值模拟方法的可行性.

表1 翼型帆试验和数值模拟的升阻力系数
进而利用软件STAR CCM+,对椭圆弧型风帆进行数值模拟,选择椭圆弧型风帆的参数:展弦比为1.3,外拱拱度比为0.15,最大厚度比为0.1.计算不同攻角下的升阻力系数及推力系数.
图6、7分别为椭圆弧型帆的网格及压力分布.图8为不同攻角下的升阻力系数.然后通过推力系数的换算公式(2),得到每个风向角下不同几何攻角的推力系数,并找出对应推力系数最大的几何攻角,如表2.进而画出最大推力系数的曲线(图9).
Cx=CLsinβ-CDcosβ
(2)

图6 椭圆弧型帆的网格

图7 压力分布

表2 不同风向角下的最大推力系数及对应的几何攻角
图8、9分别为不同攻角下的升、阻力系数CL、CD,及不同风向角下的最大推力系数Cx.

图8 不同攻角下的升阻力系数
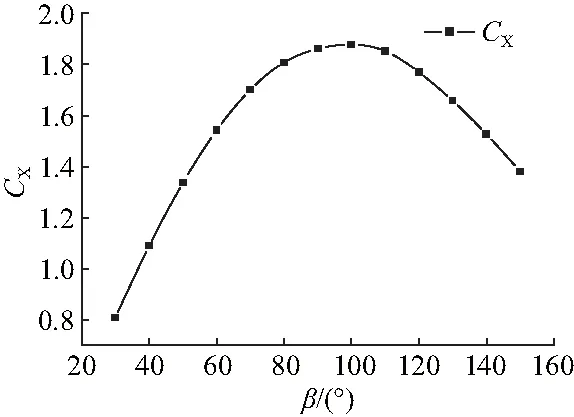
图9 不同风向角下的最大推力系数
为下面进一步研究风帆船的阻力特性,提供了风向与帆的几何攻角的较优配合.
根据模拟计算结果及表2和图8、9可得到:
(1) 升力系数随攻角的增大,先增大后减小,在攻角为15°~20°达到最大,最大升力系数约为1.86.
(2) 阻力系数随攻角的增大一直增大,且大于15°后增值较为明显.
(3) 要获得较大推力,风向角在30°~100°时,几何攻角应选15°;风向角在110°~130°时,几何攻角应选20°;风向角在140°~160°时,几何攻角应选25°.
(4) 风向角为80°~120°时,风帆具有较好的助推效果,最大推力系数可达到1.88左右.
2 裸船体的阻力预报
为了研究风帆船的阻力特性,首先对裸船体进行阻力预报,并与船模试验进行对比,验证数值模拟的可靠性.在STAR CCM+中,使用不同的多相流模型解决不同类别的多相流动,而文中采用volume of fluid model(VOF模型):此模型用于系统中包含两个或多个互不相溶的相.系统中每一相构成一个较大的结构(典型的如自由表面流)[12].
VOF方法将流体体积函数设定在单元中心,流体速度设置在网格单元的中心,根据相邻网格的流体体积函数和网格单元四边上的流体速度来计算流过制定单元网格的流体体积,借此来确定制定单元内下一时刻的流体体积函数,并根据相邻网格单元的流体体积函数来确定自由面单元内自由面的位置和形状,其满足:
(3)
利用VOF法,首先对目标船(4.5万吨散货船)进行阻力预报,并与船模试验数据对比,验证数值模拟的可靠性.船舶模型缩尺比λ=50,实船及船模的部分主尺度参数见表3.

表3 实船及船模的主要参数
为了与船模试验进行对比,模拟了从13~19 kn 7个不同船速下的模型.计算域的选取:在x轴方向,船首距离流域前端约为1.5倍船长,尾端距流域尾端为2.5倍船长;y轴方向,取2.5倍船长;z轴方向,向上约为1.5倍船长,向下约为2.5倍船长.网格模型选择表面重构、切割体网格及棱柱层网格.为了细化几何的锐角或锐边,对船的首尾进行体积网格细化.为了提高流体特征的分辨率,对开尔文尾流进行体积网格细化.通过使用切割体网格单元,在自由表面法线方向上利用各向异性细化.为了节省时间,避免反复操作,录制宏文件,简化网格加密过程.
计算方法基于有限体积法求解N-S方程,湍流模型选择K-Epsilon模型,采用VOF方法捕捉自由液面[12],并在进出口及左右边界进行阻尼消波,防止在流动阻力模拟期间发生波反射的影响[13].图10、11分别为自由面加密网格及开尔文波形网格.

图10 自由面的网格

图11 开尔文波形网格
表4中为不同航速下的船模阻力试验数据、船模试验转换成实船的阻力值及数值模拟值.图12中,数值模拟结果与试验数据两者吻合度较好,说明模拟中网格划分、边界条件设置等较为合理,可靠性得到验证.

表4 船模试验结果及数值模拟结果

图12 模拟结果与试验数据的对比
3 带帆船的阻力性能研究
3.1 直航状态下带帆船的阻力特性
在验证了裸船阻力预报的可靠性之后,进一步研究风帆船的阻力特性.武汉水运工程学院的风帆船流体动力课题组曾提出:风帆的整体宽度是船舶的最大宽度的0.9倍左右时可达到最佳的节能效果,由此选取风帆的宽度为30 m.高度与宽度的比在1.2~1.6为宜,这里高度选择39 m.风帆的数量跟船舶的布置有关,根据文献,两帆间距应大于1.2倍弦长,这样风帆之间的不利影响较小,能够使风帆有效的被应用[14],因此,文中在船上布置3个帆,相邻间距为50 m.为考虑帆与船整体的相互作用,将帆与船作为一个整体进行模拟研究[15],且按照实比例进行模拟.图13~16分别为风帆船的自由面、波形图、帆的压力分布及风帆周围的速度矢量.

图13 自由面

图14 波形

图15 风帆表面的压力分布

图16 风帆周围的速度矢量
海上风速普遍要比陆地上更大,在海平面以上高80 m处,平均风速大概8~10 m/s.当靠近陆地时,风速随粘度的变化而逐渐降低.一般假设风速满足:
(4)
式中:ur、zr分别为参考风速和参考高度;u、z分别为新的风速及高度.在海平面以上,α取0.11较为适合[16].假定海平面80 m的风速为8 m/s,则平均风速可近似估算,约为7 m/s.因此,文中将真实风速假定为7 m/s(而表观风速由矢量合成得到,如图2).航速分别为13 kn(设计航速)及16 kn,模拟结果如表5、6.

表5 设计航速13 kn时不同风向角下的受力结果

表6 航速为16 kn时不同风向角下的受力结果
表中的几何攻角由表2得出,此处的表观风向角η,即表2中提到的风向角.图17为船速Vs为13、16 kn时,不同风向下,风帆、船体和风帆及船的整体所受力F的曲线.

图17 不同风向角下的受力
为了研究风帆间的相互作用,在计算真实风向角为100°,航速为13 kn时对3个风帆分别进行监控,而模拟计算稳定后,发现帆1、帆2、帆3(由船首到船尾的顺序)提供的推力大小分别为52.8、42.6、32.6 kN.3个风帆受到的力并不相等,可见风帆会受到前面风帆的影响而使助推效果下降.因此在模拟中将其作为一个整体研究,得到的结果才更合理.
随后对分别布置两帆及四帆的相同工况进行了模拟计算.布置两帆,帆间距90 m时,帆1、帆2所提供的助推力分别为49.4、43.8 kN.而布置四帆,帆间距为30 m时,帆1、帆2、帆3、帆4所提供的推力分别为59.5、29.9、21.4、14.5kN.对比分析可知,两帆时,相互影响最小,但不能充分利用船长来布置风帆,产生的总的助推力相对较小;四帆时,相互影响很大,产生的助推效果较差,因此三帆的布置较为合理,也与文献中记载相吻合[14].
由模拟结果及图17,可得:
(1) 在真实风向角为40°~120°时,通过调节风帆的转角,均能达到一定的助推效果,当船速为13 kn时,风帆的推力可使船舶阻力减小8.7%~23.3%;当船速为16 kn时,风帆的推力可使船舶阻力减小5.4%~14.3%.
(2) 随真实风向角的增大,两种航速下风帆提供的助推力均呈先增大,后减小的趋势.
(3) 在真实风向角为80°~100°时,风帆的助推效果较好,在真实风向角为100°,船速分别为13、16 kn时,船舶阻力分别减小23.3%、14.3%.
(4) 在13、16 kn两种船速下,由于相对风速大小方向都发生变化,因此风帆提供的推力略有不同,且船速为13 kn时,风帆提供的推力相对较大.
(5) 由于船速为13 kn时,船体阻力比船速为16 kn时小很多,因此船速为13 kn时,风帆使船舶阻力减小的幅度大,助推性能高.
3.2 不同漂角下带帆船的阻力特性
在风与流的作用下,船体与船舶航行方向会产生一个转角,即漂角.由于漂角的影响,船舶的阻力特性会发生较大变化.风帆船由于船体倾斜,其湿表面积大小与正常航行时不同,摩擦阻力与正常航行时也不同,但风帆船横倾角一般不大,因此引起的湿表面积的变化也不大,为了简化分析计算,可将横倾角对摩擦阻力的影响忽略不计,根据情况不同假设漂角分别为2°、4°、6°、8°的情况进行计算分析.图18、19分别为开尔文波形网格图及流线的速度矢量.
当船速分别为13、16 kn,风速为7 m/s,实际风向角为100°时,不同漂角下的模拟结果如表7、8.

图18 开尔文波形网格

图19 流线的速度矢量
表中包括不同漂角下,船舶的船体阻力、风帆推力及帆与船体的整体阻力,文中提到的船舶阻力方向均与航行方向相反.而图20表示船速为13、16 kn时,实际风向角为100°时,不同漂角下,风帆(sail)、船体(hull)和风帆及船的整体(total)所受的力.此时由于风速、航速固定且方向保持不变,因此表观风向角不变,分别为138.9°、143.9°.所以对应取得最大推力的几何攻角也不变,均为20°.但由于漂角的变化,应该对应调整风帆的角度,使几何攻角保持在20°(若漂角为2°,对应风帆反向调整2°).

表7 航速为13 kn时不同漂角下的受力结果

表8 航速为16 kn时不同漂角下的受力结果

图20 不同漂角下的受力
由模拟结果及图20,可得:① 与直航状态相比,随着漂角的增大,船体的阻力逐渐增大;② 随着漂角的逐渐增大,船舶阻力增大的幅度越来越大;③ 随着漂角的增大,风帆提供的推力相对稳定且略有减小;④ 随着漂角的增大,虽然风帆提供的推力变化不大,但船体阻力增加明显,因此风帆提供推力的比例下降明显;⑤ 小漂角时,风帆船的整体阻力要比裸船直航时小,此时风帆船有一定的优越性;而随着漂角的增大,风帆船的整体阻力要大于裸船直航的阻力,因此航行时应将漂角控制在较小的范围.
为了得出风帆船的阻力性能规律,对模拟计算结果进行综合对比发现:在裸船直航状态下,船速为13、16 kn时,船模所受阻力换算成实船阻力后分别为557.3、863.4 kN,而加装风帆后(如表5、6及图17)由于风帆的助力作用,使船舶的整体阻力明显减少,在真实风向角为100°时,阻力减少的最多,对应风速下的阻力值分别为421.6、719.3 kN,与裸船状态相比,分别减少约23.3%、14.3%.而随着船舶漂角的增加(如表7、8及图20)船舶整体阻力值明显增加,在漂角较小时(小于4°),阻力增值相对较小,而漂角大于4°时,阻力增值很大,风帆的助推效率也明显下降.当漂角达到8°,船速为13、16 kn时,风帆船的整体阻力已经大于裸船直航下的阻力,分别达到563.1、965.8 kN,虽然风帆提供的助推力变化不大,但由于漂角的增加,船体阻力增值很大.可见加装风帆后,若产生漂角较大,则不利于航行.因此今后还应对舵角的影响做进一步的研究,通过舵帆配合的调整,使漂角控制在较小的范围内.
4 结论
(1) 椭圆弧型风帆在真实风向为40°~120°时,可通过风帆几何攻角的调整,达到较优的助推效果,当船速为13 kn时,风帆的推力可使船舶阻力减小8.7%~23.3%;当船速为16 kn时,风帆的推力可使船舶阻力减小5.4%~14.3%.随真实风向的增大,两种航速下风帆提供的助推力均呈先增大,后减小的趋势.
(2) 随着船舶漂角的增加,船舶整体阻力值增加,且增加幅度越来越大,在漂角较小时(小于4°),阻力增值相对较小,而漂角大于4°时,阻力增值很大,风帆的助推效率也明显下降.
(3) 小漂角下,风帆船的整体阻力要比裸船直航时小,此时风帆船有一定的优越性;而随着漂角的增大,风帆船的整体阻力要大于裸船直航的阻力,因此航行时应将漂角控制在较小的范围.
References)
[1] 肖丹.基于CFD的船舶阻力性能研究[D].大连:大连理工大学,2014.
[2] 郑小龙,黄胜,尚秀敏.基于CFD的船舶阻力预报方法研究[J].江苏科技大学学报(自然科学版), 2014,28(2):109-113.DOI:10.3969/j.issn.1673-4807.2014.02.002.
ZHENG Xiaolong,HUANG Sheng,SHANG Xiumin.Study of ship resistance prediction method based on CFD[J].Journal of Jiangsu University of Science and Techonlogy(Natural Science Edition), 2014,28(2): 109-113. DOI:10.3969/j.issn.1673-4807.2014.02.002.(in Chinese)
[3] 郭帅.风帆优化及助航节能应用研究[D].大连:大连海事大学,2012.
[4] 于小虎,刘寅东,张英俊,等.船舶风帆助航节能效果[J].大连海事大学报, 2011, 37(4):35-38.
YU Xiaohu,LIU Yindong,ZHANG Yingjun,et al.Energy saving effect of sail-assisted ship[J].Journal of Dalian Mar-itime University,2011,37(4):35-38.(in Chinese)
[5] 杨烨.“文竹海”轮风帆助航时船机桨帆配合操纵分析[D].大连:大连海事大学, 2010.
[6] 陈鲁愚,陈顺怀,严新平.大型远洋风帆助航船舶节能效率分析[J].船海工程. 2010, 39(6):123-128.DOI:10.3963/j.issn.1671-7953.2010.06.033
CHEN Luyu,CHEN Shunhuai,YAN Xinping.Analysis on energy conservation of sail-assisted ocean-going vessel [J].Ship and Ocean Engineering. 2010, 39(6): 123-128.DOI:10.3963/j.issn.1671-7953.2010.06.033(in Chinese)
[7] OUCHI K. UZAWA K. KAMAI A, et al. “wind cha-llenger”the next generation hybrid sailing vessel[C]∥Third International Symposium on Marine Propellers smp′13.Launceston, Tasmania,Australia, 2013: 562-567.
[8] LONGO J, STREN F. Effects of drift angle on model ship flow[J]. Experiments in Fluids, 2002,32(5):558-569. DOI: 10.1007/s00348-001-0397-0.
[9] 曾向明,胡以怀,王友聪.不同形状风帆的风洞试验[J].上海海事大学学报, 2010, 31(4):28-31.
ZHENG Xiangming,HU Yihuai,WANG Youcong.Wind tunnel test on sails with different shape[J].Journal of Shanghai Maritime University, 2010,31(4):28-31.(in Chinases)
[10] 王宏明,吴桂涛,杨昺崧.基于CFD的风帆助航技术效能分析[J].中国造船,2011, 52(2):25-33.
WANG Hongming,WU Guitao,YANG Bingsong. Efficiency analysis of sail-assisted ship based on CFD [J]. Ship Building of China, 2011, 52(2):25-33.(in Chinases)
[11] 钱翼稷.空气动力学[M].北京:北京航空航天大学出版社,2009.
[12] HIRT C W, NICHOLS B D. Volume of fluid method for the dynamics of free boundary [J]. Compute Phys, 1981(39): 201-225.
[13] JUNWOO C, SUNG B Y. Nu-merical simulations using momentum source wave-maker applied to RANS equation model [J]. Coastal Engineering, 2009,56 (10):1043-1060.
[14] 李文博.风帆训练舰线型设计与航行性能研究[D].哈尔滨:哈尔滨工程大学, 2010:21-26.
[15] FUJIWARA T, HEAN G E, KITAMURA F I. Sail-sail and sail-hull in-teraction effects of hybrid-sail assisted bu-lk carrier [J]. Journal of Marine Science & Technology, 2005, 10(2): 82-95. DOI: 10.1007/s00773-005-0191-4.
[16] KRAMER J A. Hydrodynamic perfo-rmance of sail-assisted merchant vessels [D].Norway:Norwegian University of Science and Technology, 2014.

