月池对振荡浮子式波能装置转换效率的影响
王树齐,张万超,徐 刚
(江苏科技大学 船舶与海洋工程学院, 镇江 212003)
随着全球对能源和电力需求的逐步增加[1-4],在过去的几十年里,从海浪中提取能量并将其转换成可用能量的理论和方法已经被大量提出.随着计算机和实验水平的不断发展,如何通过理论或实验研究来最大限度地提高转换效率等问题受到越来越多的关注.目前,在各种形式的波能转换装置中,作为直驱的振荡浮子型波能装置,其波能俘获能力的研究,对其他形式的波能转换装置研究具有重要借鉴意义.
振荡浮子式波能装置利用浮子在波浪中相对于海底或平台的运动,激励PTO(power take-off)系统做功,进而输出能量.因而对该类型装置的优化主要集中于浮子水动力特性及PTO系统性能.其中,浮子水动力特性的研究基于其构型、尺寸及阵列布置方式的变化.文献[5]中研究了常规垂直轴对称型浮子在添加不同附属结构后的水动力特性,发现浮子的附加构件能很好地促进浮子波能转换能力.文献[6]中针对波斯湾的阿萨卢耶港的海域情况,通过改变浮子构型进而改变其固有频率,设计了一种适合该海况的锥形浮子.文献[7]中找到了一种针对浮子构型的优化方法,并运用该方法为爱尔兰西海岸海域设计了一种双浮子波浪能发电装置.
针对PTO系统的优化主要包括改变其弹簧刚度,进而改变装置振荡频率以及PTO阻尼以改变其负载.最早关于这方面的研究来自于文献[8-9],发现当浮子运动速度与波浪激励力没有相位差时,浮子获得能量达到峰值.基于这种方法,文献[10]中发明了一种称为“Norwegian”的波浪能装置,这种装置的PTO物理参数可以进行控制,使得浮子能高效地转换能量.文献[11]中针对单一圆柱及复杂圆柱形波浪能装置,分别对浮子构型及PTO系统参数进行了优化.
基于振荡浮子式波能装置,通过改变振荡浮子构型及动力输出阻尼来优化其转换效率,会取得较为满意的结果,但在实际海况中,这些优化方法尤其是关于PTO系统控制很难在工作中实现.事实上,通过在流场中增加附属装置,进而改变流场环境也能改变浮子水动力性能,而且比较好实现,而目前关于这方面的研究还很少.文中提出了一种基于月池结构的波能装置模型,通过改变月池上下入口的尺寸来改变月池内浸没圆盘(振荡浮子)的运动特性.运用线性微幅波假设,计算了在同等弹簧刚度及输出阻尼下,圆盘在有无月池结构下的俘获宽度比,得到了其转换效率放大系数,为后续振荡浮子波浪能发电装置优化研究提供依据.
1 波能转换数学模型
基于月池结构的波能装置模型如图1,上部半径为RE,下部入口半径为RT的薄壁月池结构浸没于水中,假定一与月池同轴、半径为RM的薄圆盘浸没于月池中,上沿、变截面处、下沿及圆盘距水平面的距离分别为e、t、d、b,h为水深.
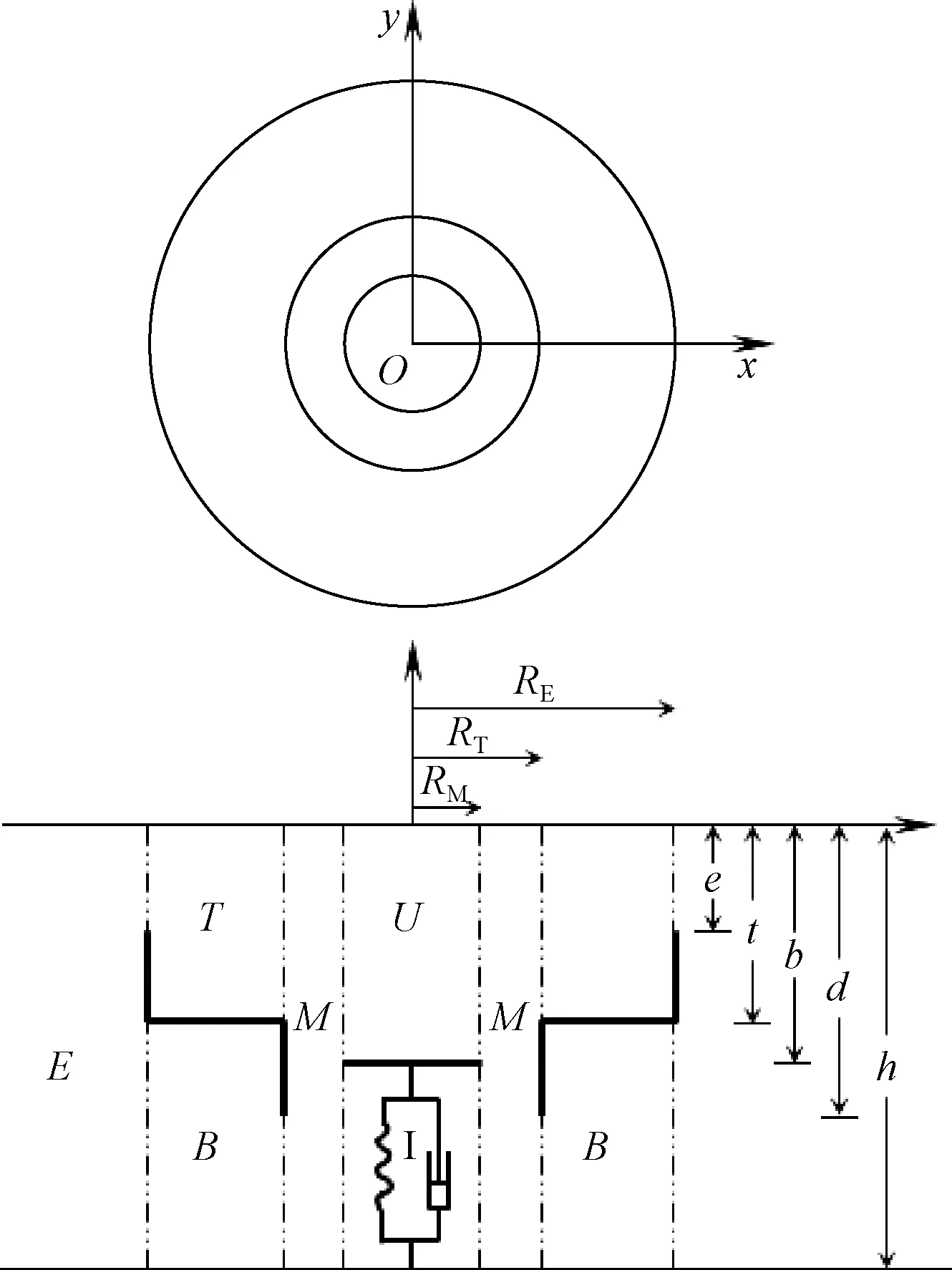
图1 装置及流域划分示意
在柱坐标系下引进速度势Ψ(r,θ,z,t)来描述流场运动:
Ψ(r,θ,z,t)=R{Φ(r,θ,z)e-iωt}
(1)
式中,Φ(r,θ,z)需满足Laplace方程、物面条件及自由面条件:
2Φ=0; ∂nΦ=Vn;f2Φ-∂zΦ=0,z=0
(2)
式中:(r,θ,z)为柱坐标系下对应的空间变量;Vn为物面法向速度;z=-h时,Vn=0;f2=w2/g,w为频率;g为重力加速度.另外,在无穷远处,波能装置对流域的影响可以忽略不计,那么入射波速度势可表示为:
(3)
式中:A,w,k0分别为入射波波幅、频率及波数,k0由色散方程k0tankk0h=f2计算得到.
考虑到外部线性输出阻尼及弹簧刚度,根据牛顿第二定律,圆盘在波浪中垂荡运动方程可表达为:
(4)
式中:m为圆盘质量;Z为圆盘垂向位移;Fd、Fr和Fm分别为波浪激励力、辐射力及PTO载荷.基于线性波理论,引入线性输出阻尼,圆盘受到的垂向波浪激励力及负载可表示为:
(5)
式中:Z(t)=zexp(-iwt),Fd(t)=fdexp(-iwt);μ、λ分别为圆盘垂向附加质量及阻尼系数;k、c分别为弹簧刚度及输出阻尼.联立方程式(4~5)可得圆盘垂向有阻尼强迫振动方程及其固有频率[12]:
(6)
作为波能获取装置,当装置固有频率等于波浪入射频率时,会发生共振,由此可得最佳PTO刚度及相应获取的波浪能平均功率:
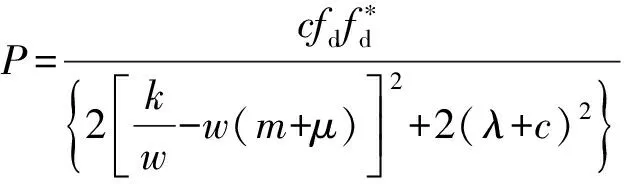
(7)
那么,当∂cP=0时,波能装置获取的能量最大,则可得到最佳PTO阻尼copt、最优功率Popt及最优转换效率ηopt:
(8)
式中:P0为浮子宽度内波浪的输入功率,可表示为:
(9)
2 波能装置水动力分析
假定圆盘在不可压、流动无旋的流场中作微幅垂荡运动,为了计算圆盘的附加质量、辐射阻尼及垂向激励力,流域绕射势Φ7和垂向辐射势Φ3可表示为:
(10)
式中,φ为空间速度势,需要满足拉普拉斯方程、自由面条件、物面条件及无穷远处边界条件.运用特征函数展开及边界匹配法,根据装置特点,可将流域划分为如图1的子域.结合各子域边界条件,对各子域速度势采用离变量法[13],可得到各子域速度势无穷级数表达形式:
(11)
(12)
(13)
(14)
(15)
(16)
式中:
k0tanhk0h=f2
kntanknh=-f2n=1,2,3…
γ0tanhγ0h=f2
γntanγnh=-f2n=1,2,3…
运用各子域耦合面处压力及速度连续性,可以得到速度势表达式中的未知系数,根据各子域速度势,可得圆盘在波浪中振荡的激励力及相关水动力系数:
(17)
3 数值计算结果
文中的主要目的是研究月池结构对振荡浮子波浪能转换效率的影响.为便于研究和分析月池结构在此过程中的作用,假定月池结构及振动圆盘部分参数为常量,其中月池结构上下入口及变截面处距静水面分别为3.0、11.0、5.0 m, 振荡圆盘半径为4.0 m浸没于自由面下8.0 m处,水深为60 m.
基于势流理论[14],通过解析法研究月池结构及振荡圆盘水动力特性,为验证文中方法及速度势求解的正确性,针对4种月池构型,运用边界元法对圆盘在月池中的水动力性能进行了计算,对比本方法计算结果如图2,图中线条为本方法计算结果,数据点为边界元法计算的结果.边界元法是一种很好的求解结构水动力学问题的数值计算方法,经过几十年的发展,已经在诸多领域得到广泛应用.采用边界元法仅需在计算域的边界上进行求解即可,其可将三维问题转化为二维问题,或者将二维问题转化为一维问题,且能方便处理无界区域问题,这也是边界元法在求解船舶水动力学势流绕流问题中得到广泛应用的重要原因之一.从图中可以看出,两种方法结果是一致的,验证了文中方法的有效性.
此外,由图还可以看出,月池结构对振动圆盘的水动力特性有较大的影响,当月池下部入口尺寸固定时,随着上部入口的增大,其波浪激励力也逐渐增大,而激励力峰值对应的频率逐渐减小;附加质量在低频部分逐渐增大,在较高频率处受到的影响较小;辐射阻尼在低频部分随着其增大出现负值,在频率为1.0 rad/s附近,逐渐增大,在高频部分受到的影响较小.当辐射阻尼出现负值时,此时波浪能装置PTO阻尼需要做出调节.
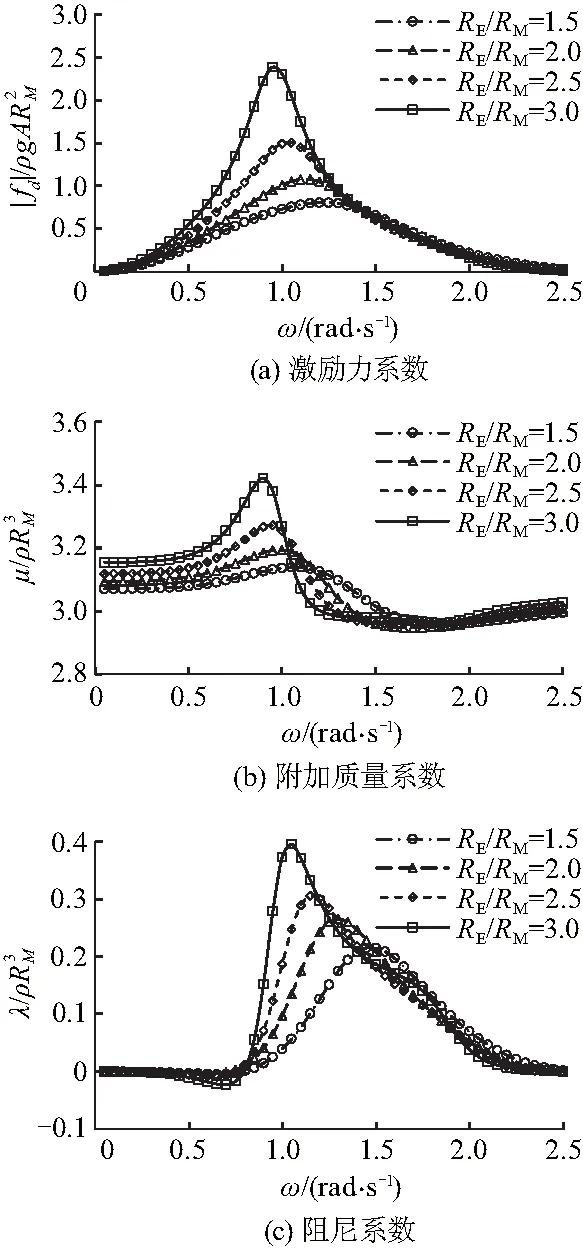
图2 RT/RM=1.2,两种方法计算的圆盘水动力系数
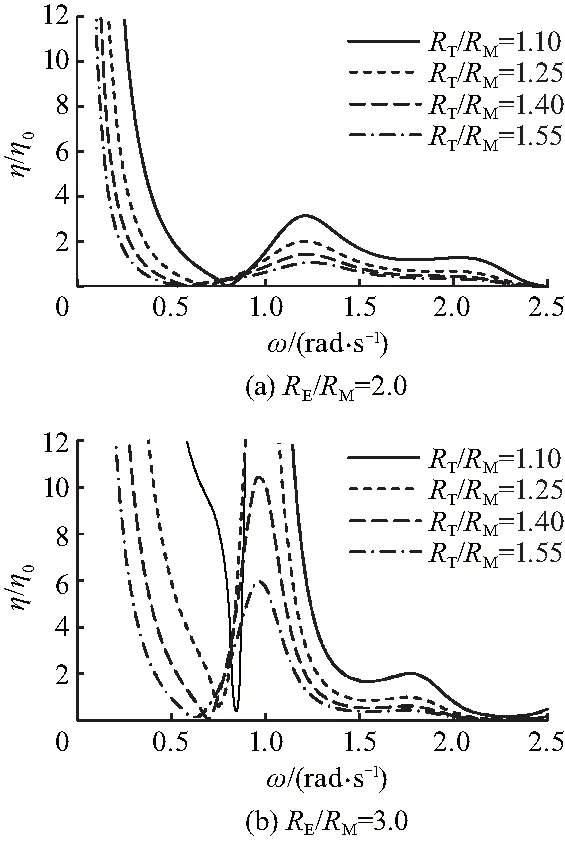
图3 RE/RM给定,RT/RM变化的效率放大系数
为研究月池构型及尺寸对浸没圆盘获能效率的影响,避免单个圆盘尖端共振[13]的影响,计算了给定圆盘在不同构型月池和无月池情况下的波能转换效率比,结果如图3、4,图中:η0为浸没圆盘在没有月池结构下的最优波能转换效率;η为圆盘在月池结构下的最优转换效率.

图4 RT/RM给定,RE/RM变化的效率放大系数
图3描述了振动圆盘在月池上部入口给定,下部入口变化时的波浪能转换能力.可以看出:月池结构在一定频率范围内能够促进浮子转换波浪能,文中称此频率为有效频率,如图3(a);当RT/RM=1.4时,有效频率范围为(0,0.35)及(1.05, 1.4),当波浪频率不在此范围,月池结构将起到抑制作用.而随着RT/RM的逐渐减小,这个有效频率范围随之发生变化,如图3(b)中当RT/RM分别为1.55, 1.4, 1.25, 1.1时,低频部分其相应的有效频率范围为(0, 0.45),(0, 0.6),(0, 0.7),(0, 0.8),而高频部分为(0.75, 1.25),(0.75, 1.3),(0.8, 1.4),(0.9, 1.95).由此可以看出,当选定波浪能装置工作海域,可以通过改变月池装置结构尺寸来改变其有效频率范围.
同样地,当给定月池下部入口半径,而外部半径变化时,月池对振动浮子波浪能转换效率的影响如图4.可以看出,当给定月池内部半径,外半径增大能增大低频部分有效频率范围,而高频部分有效频率范围下限向低频方向移动,而上限先减小后增大,如图4(a),当RT/RM=1.2,RE/RM分别为1.5, 2.0, 2.5, 3.0时,高频部分有效频率范围分别为 (1.35, 2.4),(1.0, 1.55),(0.85, 1.45),(0.85, 1.85).
4 结论
(1) 月池结构对其内圆盘水动力特性有较大影响,月池的存在使得圆盘垂荡辐射阻尼出现负值.
(2) 通过增大月池外半径或减小内半径,均能在低频范围内增大浮子波浪能转换效率,且随着外半径增大或内半径减小,低频部分有效频率范围增大.
(3) 增大月池外半径或减小内半径会使得高频部分有效频率范围出现移动.当外部半径给定,随着内部半径减小,高频部分有效频率范围像高频部分移动且带宽增大;而当内部半径给定,增大外部半径时,高频部分有效频率范围下限向低频方向移动,而上限先减小后增大.
References)
[1] 张正敏,王革华,高虎. 中国可再生能源发展战略与政策研究[J]. 经济研究参考,2004(84):26-32.DOI:10.16110/j.cnki.issn2095-3151.2004.84.006
ZHANG Zhengmin, WANG Gehua, GAO Hu. Chinese renewable energy development strategy and policy research [J]. Review of Economic Research, 2004(84):26-32. DOI:10.16110/j.cnki.issn2095-3151.2004.84.006.(in Chinese)
[2] FALCAO A O. Wave energy utilization: a review of the technologies [J]. Renewable and Sustainable Energy Reviews, 2010, 14(3):899-918. DOI:10.1016/j.rser.2009.11.003
[3] CARAHER S L, CHICK J P, MUELLER M A. Investigation of fluid film bearings for use in direct drive linear generators in submerged wave energy converters[C]∥Proceedings of 18th International Offshore Polar Engineering Conference. Vancouver, Canada, 2008:409-416.
[4] CIEMENT A, MCCULLEN P.Wave energy in Europe: current status and perspectives [J]. Renewable and Sustainable Energy Reviews, 2002, 6(5):405-431.
[5] MAVRAKOS S A, KATSAOUNIS G M. Effects of floaters hydrodynamics on the performance of tightly moored wave energy converters [J]. IET Renewable Power Generation, 2009, 4(6):531-544.DOI:10.1049/iet.rpg.2009.0191
[6] NAZARI M, GHASSEMI H, GHIASI M, et al. Design of the point absorber wave energy converter for Assaluyeh Port [J]. Iranica Journal of Energy & Environment. 2013, 4(2):130-135.DOI:10.5829/idosi.ijee.2013.04.02.09
[7] GOGGINS J, FINNEGAN W.Shape optimization of floating wave energy converters for a specified wave energy spectrum [J]. Renewable Energy, 2014(71):208-220.
[8] MEI C C. Power extraction from water waves [J]. Journal of Ship Research,1976(20):63-66.
[9] BUDAL K, FALNES J. Interacting point absorbers with controlled motion [M]. New York:Academic Press,1980:381-399.
[10] BUDAL K, FALNES J, IVERSEN L C, et al. The Norwegian wave-power buoy project[C]∥Proceedings of 2nd International Symposium on Wave Energy Utilization. Trondheim, Norway,1982:323-344.
[11] 吴必军,盛松伟,张运秋,等. 复杂圆柱型波能装置能量转换特性研究[J]. 哈尔滨工程大学学报,2010, 31 (8): 1023-1028.DOI:10.3969/j.issn.1006-7043.2010.08.006.
WU Bijun, SHENG Songwei, ZHANG Yunqin, et al.Wave-power conversion characteristics of a complex vertical cylinder[J]. Journal of Harbin Engineering University,2010,31(8):1023-1028.DOI:10.3969/j.issn.1006-7043.2010.08.006.(in Chinese)
[12] WU Bijun, SHENG Songwei, ZHANG Yunqiu, et al. Wave-power conversion characteristics of a complex vertical cylinder [J]. Journal of Harbin Engineering University, 2010, 31 (8): 1023-1028. DOI:10.3969/j.issn.1006-7043.2010.08.006.
[13] FALCAO A F O, HENRIQUES J C C. Effect of non-ideal power take-off efficiency on performance of single and two-body reactively controlled wave energy converters [J]. Journal of Ocean Engineering and Marine Energy. 2015, 1(3):273-286.DOI:10.1007/s40722-015-0023-5.
[14] GARRETT C J R. Wave force on a circular dock [J]. Journal of Fluid Mechanics, 1971(46): 129-139.
[15] 窦培林,朱建,陈刚,等. 风浪流成长全过程单点系泊FPSO运动低频响应极值研究[J]. 江苏科技大学学报(自然科学版),2014, 28(2):114-119.DOI:10.3969/j.issn.1673-4807.2014.02.003.
DOU Peilin, ZHU Jian, CHEN Gang, et al. Low frequency extreme response of single-point moored FPSO during the whole process of growing of wind/wave/current[J]. Journal of Jiangsu University of Science and Technology (Natural Science Edition), 2014, 28(2):114-119. DOI:10.3969/j.issn.1673-4807.2014.02.003.(in Chinese)

