基于降维动态观测器的一类多项式系统的非线性H>∞控制

周燕茹,曾建平,邵振华,黄程恺

(1.厦门理工学院电气工程与自动化学院,福建 厦门 361024;2.厦门大学信息科学与技术学院,福建 厦门 361005)

在控制设计研究中,采用状态反馈的前提条件是被控对象的状态都可获知．然而,在许多实际工程系统中,一些状态往往不能直接测量,或因技术成本太高而无法进行测量．针对此种情况,可采用基于观测器的状态反馈控制方式,即通过系统输出信号来对这些不可测状态进行估计,以实现特定的控制目标．迄今,基于观测器的控制方法已受到广泛的关注,并取得了大量的研究成果[1-8]．

对线性时不变系统,Park等[1]设计了一种新型的线性动态观测器．该观测器的增益存在动态特性,可视为经典Luenberger观测器[2]在结构上的扩展,也可认为是动态输出反馈控制机制的一种对偶形式[3]．与经典的Luenberger观测器相比,动态观测器的最大优势在于可提供更多控制设计自由度．目前,动态观测器已被应用于各类控制问题研究,如传感器故障诊断的H∞控制[4]、Lipschitz非线性系统的H∞控制[5]、不确定T-S模糊系统的鲁棒H∞控制[6]和线性广义系统的H∞控制[7]等．然而,这些现有成果大多采用线性控制．由于非线性系统固有的复杂性,且缺乏一般的非线性求解方法和工具,动态观测器在非线性控制领域还未能得到实质性的推广应用．

近来快速发展的多项式平方和(sum of squares,SOS)理论有力地促进了非线性系统研究,特别是在基于SOS的非线性状态反馈控制问题上取得了重大突破[8-10]．SOS可为多项式非负性判断提供有效的凸松弛算法[11]．在其框架下,一方面,许多成熟的线性控制理论可推广应用于多项式非线性系统[9];另一方面,各种带多项式约束的非线性控制问题都可转化为SOS凸规划问题．

本文中针对一类特定的多项式非线性系统,采用SOS研究基于动态观测器的非线性H∞控制问题．根据线性动态观测器形式和系统结构特征,构造出相应的非线性降维动态观测器;观测器的非线性H∞控制问题被转换为SOS凸优化问题,从而有效地避免了构造Lyapunov函数和数值仿真的困难;所得非线性观测器和控制器仅是关于系统状态的多项式或有理式函数,从工程实现的角度来看,与传统线性观测器和控制器相比,实现这种非线性观测器和控制器所增加的复杂性很有限．

1　问题描述和预备

1.1　系统描述和问题声明

考虑如下一类特定的多项式型非线性系统

(1)

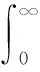
注1系统(1)具有的结构特征:1) 动力学行为由一个类线性微分方程来描述;2) 系数矩阵的元素是关于可测状态的多项式函数．许多实践和理论研究对象可以被描述为类似系统(1)的形式,如质量弹簧阻尼系统[12]、洛伦兹(Lorentz)和罗斯勒(Rossler)混沌系统[13]以及各种航天器姿态模型[9]等．

问题1基于动态观测器的非线性H∞控制问题:针对系统(1),本文中的控制目标是设计一个基于动态观测器的非线性H∞控制器,使得相应闭环系统在零平衡点渐近稳定且有L2-增益≤γ．

1.2　预备知识

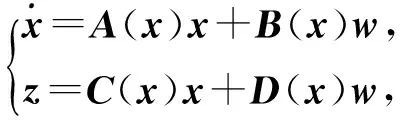
则系统的L2-增益≤γ．

定义2(SOS)[15]设f(x)是一个关于x∈Rn的多项式,如果存在一组多项式f1(x),f2(x),…,fm(x)使得

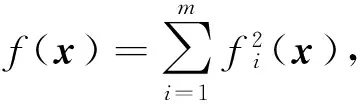
(2)

则称f(x)为SOS多项式．

显然,f(x)∈Φsos意味着对所有x∈Rn,都有f(x)≥0．SOS条件(2)也等价于存在一个常数矩阵Q≥0使得f(x)=ZT(x)QZ(x),其中Z(x)是由关于x的单项式构成的适当维列向量．

在本节的最后,给出了后续推导需要用到的两个引理．

引理2[8]设P(x)∈S[x]m对所有x∈Rn都是非奇异的,则有

2　基于动态观测器的状态反馈控制

根据系统(1)的结构特征,可构造其子状态x2的一个动态观测器．首先,由系统(1),有

(3)

(4)

(5)

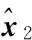
A21(x1)y+B22(x1)u+Cd(x1)xd+

(6)

(7)

于是,由式(6)和(7)即可得出系统(1)的降维动态观测器为

Dd(xJ)B21(x1))u+Cd(x1)xd,

xd=hd+Bd(xJ)y.

(8)

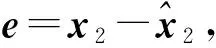
Cd(x1)xd+B12(x1)w

(9)

的零平衡点是渐近稳定的．

注3如果A(x1),B2(x1),Ad(x1),Bd(xJ),Cd(x1)和Dd(xJ)都简化为常数矩阵,则非线性观测器(8)就简化为连续时间线性时不变系统中的线性降维动态观测器．换言之,不同于该线性动态观测器,观测器(8)的参数矩阵均与系统(1)的可测子状态x1相关．在后续讨论中,将解决非线性动态观测器(8)和相应控制器的求解问题．

基于观测器(8),设计如下状态反馈控制器

(10)

(11)

再由式(1)和(9),可得

(12)

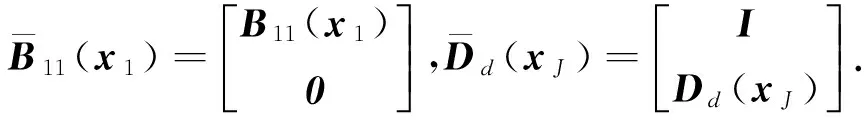
综上,结合式(9)～(12),可构成如下闭环系统:

(13)

Acl1(x1)=A(x1)+B2(x1)K(x1),

Acl4(x1)=Bd(xJ)A12(x1),

Acl3(x1)=A22(x1)-Dd(xJ)A12(x1),

Ccl(x1)=[C1(x1)+

D2(x1)K(x1)C1(x1)Q10].

对于系统(1),基于动态观测器的非线性H∞控制问题具体是指设计降维动态观测器(8)和状态反馈控制器(10),使得相应闭环系统(13)的零平衡点是渐近稳定的且有L2-增益≤γ．

根据Lyapunov稳定性理论,可先建立上述系统的一个H∞性能准则．

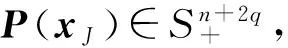
0,

(14)

则闭环系统(11)在零平衡点渐近稳定且L2-增益≤γ．

对系统(13),又有

再根据Schur补引理,由式(14)成立,可知

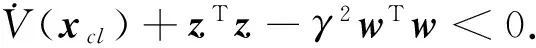
(15)

V(xcl(T))-V(xcl(0))≥0.

由定义1,又知该系统的L2-增益≤γ．

在定理1的基础上,采用SOS理论,并限定P(xJ),Ad(x1),Bd(xJ),Cd(x1)和Dd(xJ)均为多项式矩阵,可得出该基于动态观测器的非线性H∞控制问题的一个可解性条件．

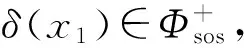
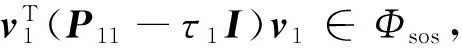
(16)

(17)

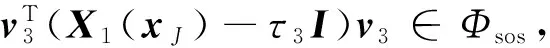
(18)

(19)

(20)

其中,v1∈Rq,v2∈Rq,v3∈Rn,v4∈R2q,v5∈Rn+2q+r+l,

Ξ1(x1)∶=He(A(x1)X1(xJ)+B2(x1)Y(x1))-

Ξ3(x1)∶=He(A22(x1)M11+Cc(x1)),

(Dc(xJ)A12(x1))T,

Ξ6(x1)∶=He(P11A22(x1)+Bc(xJ)A12(x1)),

Ξ7(x1)∶=C1(x1)X1(xJ)+D2(x1)Y(x1)．

此时,控制器增益矩阵及观测器参数矩阵分别为

Dd(xJ)=Dc(xJ),

Cd(x1)=-(Cc(x1)+Dd(xJ)

Dd(xJ)A12(x1))M11-P12Bd(xJ)

(21)

其中,P12和M12是可逆矩阵且满足

(22)

证明根据定义2,由条件(16)～(20)成立,可知

P11>0,M11>0,X1(xJ)>0,

(23)

(24)

由式(24),易知P2>0等价于

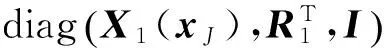
Y(x1)=K(x1)X1(xJ),

Ac(x1)=P11(A22(x1)-Dd(xJ)A12(x1))M11-

Bc(xJ)=-P11Dd(xJ)+P12Bd(xJ),

Dc(xJ)=Dd(xJ),

就可得出Ξ(x1)<0．

综上所述,条件(23)是式(14)成立的一个充分条件．根据定理1,可知该基于动态观测器的非线性H∞控制问题可解,且相应控制器和观测器的增益能通过式(21)来构造．

注4在定理2中,X1(xJ)所有元素的最高阶数应为偶数,这是式(18)成立的前提条件．

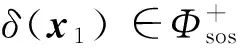
注6对于式(21),在求出P11和M11之后,可以通过矩阵I-P11M11的奇异值分解来得到可逆矩阵P12和M12．

3　数值仿真

为验证所得非线性H∞控制设计方法的可行性和有效性,针对质量弹簧阻尼系统,采用MATLAB/SOSTOOLS[8]进行控制设计求解,并给出相应的仿真效果图和分析结论．

以文献[12]中的非线性质量弹簧阻尼系统(如图1所示)为仿真对象,其动力学方程为:

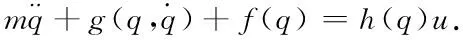
图1　质量弹簧阻尼系统Fig.1 Mass-spring-damper system

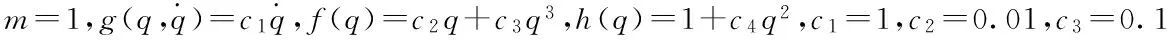
(25)

对上述系统,J=ø,故X(xJ),Bc(xJ)和Dc(xJ)为常数矩阵．设定Ac(x1)、Cc(x1)和Y(x1)的最高阶为2阶,并给定仿真参数γ=0.9,δ(x1)=10-5,τi=0.1(i=1,2,3,4)．根据定理2,系统(25)的基于降维动态观测器的非线性H∞控制问题可解,所得结果具体如下:

控制器增益矩阵为

K(x1)=

观测器参数矩阵为

6.251 0,

Bd(xJ)=13.407 1,

0.850 9,

Dd(xJ)=-0.789 6．

(i) 标称系统(nominal system,NS):w=0;

(ii) 受扰系统1(disturbed system 1,DS1):

(iii) 受扰系统2(disturbed system 2,DS2):

w=

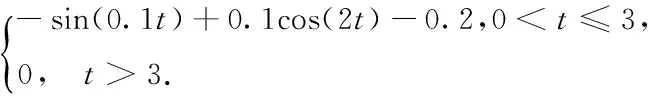
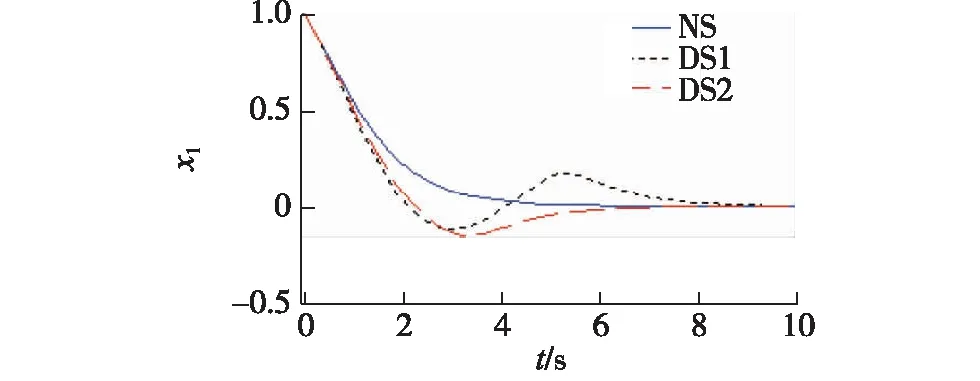
图2　x1的时间响应曲线Fig.2 Trajectories of x1

图和x2的时间响应曲线Fig.3 Trajectories of and x2

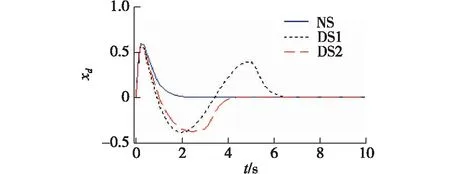
图4　xd的时间响应曲线Fig.4 Trajectories of xd

图5　控制输入u曲线Fig.5 Control input u

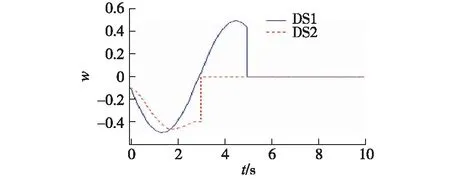
图6　外部干扰w曲线Fig.6 External disturbances w

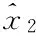
4　结　论

借鉴线性动态观测器形式和变量替换法研究思路,本文中针对一类特定的多项式系统,采用Lyapunov稳定性理论结合SOS方法,给出一种基于动态观测器的非线性H∞控制设计方法．该方法可借助有效凸优化算法进行检验,在一定程度上解决了非线性系统的计算困难,且相应控制器仅是关于系统状态的多项式或有理式函数,易于工程实现．仿真结果表明,所得控制器能保证相应闭环系统在零平衡点渐近稳定,且对外部扰动具有较强抑制能力．当然,考虑到工程实际系统往往存在着各种不确定性,可在本文工作基础上进一步研究基于动态观测器的非线性鲁棒控制问题．

参考文献：

[1]PARK J K.The concept and design of dynamic state estimation[C]∥Proceedings of the American Control Conference.San Diego:IEEE,1999:2412-2416.

[2]BOYD S,GHAOUI L E,FERON E,et al.Linear matrix inequalities in system and control theory[M].Philadelphia:Society for Industrial and Applied Mathematics,1994:111-118.

[3]PARK J K,SHIN D R,CHUNG T M.Dynamic observers for linear time-invariant sys-tems[J].Automatica,2002,38(6):1083-1087.

[4]PERTEW A M,MARQUEZ H J,ZHAO Q.H∞dynamic observer design with application in fault diagnosis[C]∥Proceeding of the 44th IEEE Conference on Decision and Control.Seville:IEEE,2005:3803-3808.

[5]PERTEW A M,MARQUEZ H J,ZHAO Q.H∞observer design for Lipschitz nonlinear systems [J].IEEE Transactions on Automatic Control,2006,51(7):1211-1216.

[6]GOLABI A,BEHESHTI M,ASEMANI M H.H∞robust fuzzy dynamic observer-based controller for uncertain Takagi-Sugeno fuzzy systems[J].IET Control Theory and Applications,2012,6(10):1434-1444.

[7]WANG Z H,LI L L,ZHANG Y,et al.Dynamic observer design for linear descriptor systems[C]∥Proceedings of the 33rd Chinese Control Conference.Nanjing:Shanghai Scientific & Technical Publishers,2014:3036-3040.

[8]PRAJNA S,PAPACHRISTODOULOU A,WU F.Nonlinear control synthesis by sum of squares optimization:a Lyapunov-based approach[C]∥Proceedings of the 5th Asian Control Conference.Melbourne:IEEE,2004:157-165.

[9]周燕茹,黄文超,曾建平.挠性卫星姿态非线性局部镇定控制[J].控制理论与应用,2014,31(3):279-284.

[10]XU J,XIE L H,WANG Y Y.Simultaneous stabilization and robust control of polynomial nonlinear systems using SOS techniques[J].IEEE Transactions on Automatic Control,2009,54(8):1892-1897.

[11]HUANG W C,SUN H F,ZENG J P.Robust control synthesis of polynomial nonlinear systems using sum of squares technique[J].Acta Automatica Sinica,2013,39(6):799-805.

[12]ZHENG Q,WU F.Nonlinear output feedbackH∞control for polynomial nonlinear systems[C]∥Procee-dings of the 2008 American Control Conference.Washington:IEEE,2008:1196-1201.

[13]LAM H K.Chaotic synchronisation using output/full state-feedback polynomial controller [J].IET Control Theory and Applications,2010,4(11):2285-2292.

[14]LU W M,DOYLE J C.H∞Control of nonlinear systems via output feedback:controller parameterization[J].IEEE Transactions on Automatic Control,1994,39(12):2517-2521.

[15]PRAJNA S,PAPACHRISTODOULOU A,SEILER P,et al.SOSTOOLS:sum of squares optimization toolbox for matlab:user′s guide version 2.0[EB/OL].[2013-01-31].http:∥www.cds.caltech.edu/sostool/.

[16]GAHINET P,APKARIAN P.A linear matrix inequality approach to H∞control[J].International Journal of Robust and Nonlinear Control,1994,4(4):421-448.