重力作用下轴对称非稳态渗流压强场的解析解

刘智颖,彭文耀,章成广*

(1.油气资源与勘探技术教育部重点实验室(长江大学),2.长江大学地球物理与石油资源学院,湖北 武汉 430100;3.江汉石油管理局有限公司测录井工程公司,湖北 潜江 433123)

通过注水来增大储层内的压强是各大油田常用的增产或稳产的手段．注水进入地层使地层中的注水压强增大,从而驱替地层中的油气进入生产井以提高采收率．为了准确描述地层中的注水压强分布状况,从而计算渗流速度并预测注水效果和生产井中的产量,需要建立渗流力学方程并求解出不同条件下的渗流场注水压强分布函数．

前人进行过许多相关研究,主要研究内容及成果可分两类．一类是渗流力学方程的建立,包括单相线性渗流方程、两相线性渗流方程、稠油非线性渗流方程[1]等,主要是给定边界条件和初始条件,求解这些方程即可得出地层中注水压强分布函数[2-3]．另一类是渗流力学方程的求解方法,该方法可分为数值解法和解析解法．数值解法的研究成果较多,如用有限差分法计算公路隧道附近区域的渗流场[4]、水库大坝中的渗流场[5]以及用有限元法求解低渗油藏开采过程中注水压强分布状况[6-7],人工压裂后地层流体压强分布状况[8]等．由于绝大多数渗流力学方程的定解问题无法解析求解,且解析解的形式大都比较复杂,因而解析解法的研究成果较少．尽管如此,解析解不仅是数值解的重要理论基础之一,而且计算程序比较容易实现,因而也是常见的研究课题．主要成果有平面径向注水压强分布函数[9-10]、柱坐标下非达西渗流力学方程的解析解[11]以及非线性三参数模型[12-14]等．这些解析解主要是基于平面径向稳定渗流模型求出的．该模型的基本假定为:径向上供水边缘的压强最大,生产井内压强最小;纵向上压强不变,且地层中注水压强分布状况稳定,不随时间变化．因此,该模型不仅未考虑重力作用下注水压强随深度增大而增大的特点,也未反映注水压强随时间变化的过程,因而难以准确描述驱替过程中注水压强的分布状况[9-10]．事实上,由于注入水受到重力的作用,供水边缘的注水压强随深度增大而增大;此外,渗流过程中注水压强分布状况会不断发生变化．这种情况下,方程的供水边缘的压强边界条件是一个与深度和纵向压强梯度有关的函数,属于非齐次边界条件,而且方程还包含时间项,使得求解过程更加复杂．针对该问题,本研究采用分离变量法将非齐次问题转化为齐次问题后再求方程的解析解,并将其应用于石油开采过程中注水后的产液量预测,验证所求解析解的正确性．

1　注水压强分布函数满足的微分方程

根据文献[10],平面径向注水压强分布函数p与井中秒产量Q分别为:

(1)

(2)

其中,pw是井壁的压强,pe是供水边缘的压强,r0是供水边缘到生产井井轴的距离,rw是生产井半径,K是地层渗透率,h是地层厚度,μ是流体黏度．

为研究注水压强分布状况随时间的变化过程,下面以地层上界面为原点,竖直向下的方向为z轴(图1),建立二维柱坐标系,求解二维轴对称非稳态单相渗流压强场方程(亦称输运方程)[10,15-16]:

(3)

其中,r、z分别是极径坐标和高度坐标,t是时间,κ=K/μCt为地层导压系数[10],Ct为地层综合压缩系数[10]．

假设目的层是渗透性地层,上下围岩为非渗透地层,则层界面附近渗流速度垂直于层界面的分量为零．由于渗流速度往往很小,可以认为供水边缘的注水压强等于静水压强．这样,方程(3)的边界条件和初始条件分别为

供水边缘的压强边界:p|r=r0=pe+ρgz,

(4)

生产井处的边界:p|r=rw=pw,

(5)

(6)

地层中初始压强值:p|t=0=p0,

(7)

其中,ρ是注入水密度,g是重力加速度,p0为地层中的初始压强值,可近似看作常数．

2　注水压强分布函数的求解过程

方程(3)可用分离变量法求解,但若使用分离变量法则会因径向非齐次边界条件式(4)和(5)而无法求解．因此,需要先将供水边缘的非齐次边界条件化为齐次边界条件再求解方程(3)．

2.1　供水边缘非齐次边界条件的处理方法

令p=I(r,z)+K(r,z,t),其中I(r,z)是一个满足边界条件式(4)和(5)的调和函数,则K(r,z,t)满足式(3)．然而,经过这种简单变型后虽然可使函数K(r,z,t)在r=r0处的边界条件转化为齐次的,但在z=±h处的边界条件却变为非齐次的,仍然难以求解．因此,需要进一步将函数K(r,z,t)分解为U(r,z)、V(r,z)和H(r,z,t)之和,使得U(r,z)和V(r,z)均满足二维轴对称拉普拉斯方程,并保证z方向至少有一个边界条件是齐次的;H(r,z,t)满足输运方程,且边界条件均为齐次的．这样,上述3个函数满足的定解问题均可以用分离变量法求解析解．具体的变型结果如下:

p(r,z,t)=I(r,z)+U(r,z)+

V(r,z)+H(r,z,t),

(8)

这样,U(r,z)、V(r,z)和H(r,z,t)分别满足

(9)

(10)

(11)

不难证明,函数U(r,z)、V(r,z)和H(r,z,t)之和满足的边界条件与方程(3)的边界条件等价．此外,由于这3个函数值均有限且与时间无关,因此只要r满足rw≤r≤r0,就有

p|t=0=H|t=0+U(r,z)+V(r,z)+

I(r,z)≡p0,

因此,经上述变型后,式(11)的初始条件与式(7)等价．

2.2　方程的求解步骤

2.2.1求解U(r，z)与V(r，z)之和

U(r,z)和V(r,z)均满足拉普拉斯方程．由分离变量法,可得到其通解[17]．这里仅写出U(r,z)的求解过程,V(r,z)的求解过程与之类似,不做赘述．

由于U(r,z)在r方向上满足第一类齐次边界条件,因此其通解形式为

(12)

将U(r,z)在z方向上的边界条件代入式(12)得

(13)

(14)

(15)

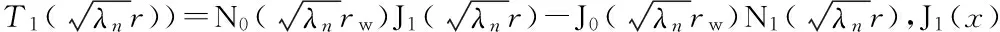
由式(13)可得Bn=An．因此,式(14)可简化为

(16)

(17)

将式(17)代入式(12)即可确定U(r,z),同理可求出V(r,z)．

令W(r,z)=U(r,z)+V(r,z),则有

(18)

其中，

2.2.2求解H(r,z,t)

式(11)同样可以采用分离变量法求解．令H(r,z,t)=R(r)Z(z)T(t),则式(11)可分解为关于R(r)、Z(z)和T(t)的常微分方程．不妨设α和β分别为函数T(t)和R(r)的本征值．通过分析α和β的取值范围可知,当且仅当0<β≤α时,式(11)存在满足边界条件的解．这样,式(11)的通解形式为

(19)

Bm0≡0,

(20)

(21)

将式(20)和(21)代入式(19)得

(22)

将式(11)的初始条件代入式(22),可得

H(r,z,0)=p0-I(r,z)-W(r,z),

(23)

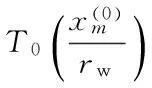
(24)

(25)

(26)

这样

(27)

其中,

将式(27)代入式(24)和(25)得

(28)

(29)

将式(28)和(29)代入式(22)即得H(r,z,t),故P(r,z,t)也随即确定．

函数P(r,z,t)需要用程序进行计算．下面给出计算程序中涉及的变量及相关算法的实现过程．程序将r方向和z方向的长度r0和h分别设定为700和20 m．W(r,z)函数的级数项数n取60,H(r,z,t)函数的级数项数m取130、q取50．式(11)中μ值采用精度较高的12阶高斯-洛巴托公式进行计算,该公式中勒让德多项式的导数采用步长为5×10-3的4步理查森外推公式进行计算．

2.3　求解方法的推广

根据以上推导过程,本研究提出了一种径向第一类非齐次边界条件和纵向第二类齐次边界条件下的二维轴对称输运方程的解析解法．为不失一般性,现将方程(3)中的p改作u．这样,方程(3)及其边界条件和初始条件分别为

(30)

u|r=r0=ξ(z)，u|r=r1=η(z)，

其中,r0>r1．

求解步骤如下:

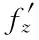
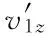
3) 用分离变量法求出v1(r,z)、v2(r,z)和w(r,z,t)，即得式(30)的解．

需要指出,若ξ(z)和η(z)均为z的一次函数,即ξ(z)=a0+b0z，η(z)=a1+b1z，则f(r,z)可选取

f(r,z)=a1+b1z+

(31)

式(31)的意义在于,若同时考虑供水边缘和生产井井壁处的z方向的压强梯度,则利用上述方法同样可以求出地层中的注水压强分布函数．

图2　不考虑供水边缘纵向压强梯度时的注水压强分布状况Fig.2 The distribution of injection pressure while ignoring the vertical pressure gradient at the injection edge

3　求解结果的检验及其应用

3.1　求解结果的检验

检验求解结果正确性的最简单方法是证明当g=0且t→∞时,式(8)与式(1)等价，即若不考虑重力及时间,检验式(8)是否与式(1)吻合．不难发现,当g=0时,I(r,z)退化为式(1),且W(r,z)≡0;当t→∞时,有H(r,z,t)≡0．因此,当g=0且t→∞时P(r,z,t)由较复杂的级数式退化为式(1),说明式(8)的求解方法及结果正确．

本研究根据程序计算结果绘制了两种条件下注水压强分布图以及注水压强曲线．供水边缘压强pe设为1.2 MPa;生产井井眼半径rw设为0.101 6 m;井壁压强pw设为1.0 MPa．图2给出了不考虑供水边缘的纵向压强梯度,也就是g=0条件下的注水压强分布图．图2(a)和(b)分别为注水后第15天和注水后第3个月时地层中的注水压强分布图．其中,图2(a)为r> 670 m范围内的注水压强分布情况．由图可见,注水压强随r的减小而减小．图2(a)中较高的压强主要集中于r> 685 m的区域,而图2(b)中集中于r> 64 m的区域．说明注水后,注水压强较高的区域逐渐接近生产井．图2(c)为不同时刻的注水压强与r的关系曲线．可以看出,注水第15天时注水压强不为零的区域主要在r> 500 m的区域;第90天时,注水压强分布状况趋于稳定且与式(1)的计算结果基本吻合．

下部压强随z坐标值增大,地层导压系数κ设为100 cm2/s,注入水密度ρ设为1.0 t/m3,重力加速度g设为9.8 m/s2,地层厚度h设为20 m,其余参数与图(2)中相同．图3中给出了考虑供水边缘的纵向压强梯度．可以看出,地层底部的注水压强明显高于顶部,说明地层底部因重力作用而产生了较高的注水压强．然而,随着时间的推移,r> 685 m,z< 4 m的区域有一个注水压强较低的区域(称压强异常区)(图3(b))．不难发现,该区域的注水压强随r的减小而增大．这与实际情况不符．产生该问题的原因是本研究仅在供水边缘的边界条件(式7)中考虑了重力的影响,而方程(3)本身却并未考虑重力．因此,当注水压强分布逐渐趋于稳定时,供水边缘底部高压强区域的注入水会流至供水边缘顶部,从而形成了压强异常区．尽管如此,这对式(8)的实际应用效果影响不大．因为,式(8)主要应用于计算生产井中的产量．根据图3(c)和(d),压强异常区主要影响供水边缘附近的注水压强,对生产井附近的注水压强分布状况影响较小．

通过图2(c)与图3(d)的对比看出,图3(d)中注水压强与柱坐标系极径的关系曲线形状与图2(c)中曲线相似．两者的不同之处在于,图3(d)表明当z=20 m时,注水压强曲线值以及r→0时的曲线斜率均高于z=10 m和z=0,亦即地层底部的注水压强及压强梯度均较大,因而当地层中的渗透率处处相等时,底部的渗流速度较快．

图3　考虑供水边缘纵向压强梯度时的注水压强分布状况Fig.3 The distribution of injection pressure while considering the vertical pressure gradient at the injection edge

3.2　应用方法及效果

应用式(8)可以计算生产井中不同时刻的日产量．计算日产量的步骤如下:

1) 将式(8)代入达西公式求出生产井井壁处的渗流速度v．

2) 将v代入产量的计算式[10]求出秒产量Q,日产量也随即确定．

表1　江汉油田Hxx3试油层段数据

Tab.1　Data of testing interval of well Hxx3 in Jianghan oilfield

K/(10-3μm2)μ/(mPa·s)pe/MPap0/MPapw/MParw/cmCt/(10-10Pa-1)r0/mρ/(t·m-3)13.3615.314.3711.711.710.161.777401.06

下面介绍式(8)在江汉油田Hxx3井中的应用效果．该井的1 317.5～1 326.6 m层段的测井结论为油层,岩性为泥质砂岩,属于低渗地层需进行注水开采．注水后该井段的日产量随时间变化,其各时刻的试油资料为:注水后第15天,日产油0.52 m3/d;注水后第30天,日产油3.12 m3/d;注水后第60天,日产油6.36 m3/d;注水后第90天,日产油6.04 m3/d．注水层段中的渗流场可近似看作单相渗流场,与式(8)的适用条件基本吻合．详细数据见表1．

本研究应用式(8)绘制了该层段的注水压强分布图及井内流速曲线(图4),并将式(2)和(8)计算的生产井中的日产量与表1中的试油资料进行了对比(图5)．

从图4(a)和(b)中不难看出,注水90 d后,注水压强波传播到生产井处,且注水压强分布状况已趋于稳定．图4(c)是注水90 d后地层中注水压强p与柱坐标系极径r的关系曲线图．图中,虚线是将供水边缘的顶部压强pe代入式(2)的计算结果,实线是不同深度条件下式(8)的计算结果．图4(d)是生产井中不同深度不同时刻的渗流速度曲线．从图4(c)和(d)中可以看出,距离生产井井轴距离相同的位置,压强随深度增大而增大,且在r=rw附近压强梯度也随深度增大而增大．说明只要地层渗透率均匀分布,则地层中渗流速度将随深度增大而增大．

这与图3(d)的结论一致,同时还可以看出,式(1)计算的注水压强值偏小．

图4　Hxx3井的层内注水压力分布状况及渗流速度Fig.4 Formation injection pressure and the seepage velocity in well Hxx3

图5为两种方法计算的日产量与实际试油结果的对比图．通过对比不难看出,式(8)计算的日产量及其随时间变化的规律与实际试油结果比较一致,说明式(8)比式(2)更能准确计算出生产井中的日产量．此外,还能看出90 d之内,日产量逐渐增长并趋于稳定,说明注水开始后,地层中压强波的传播过程需要时间,因而生产井中的日产量并不会迅速提高．

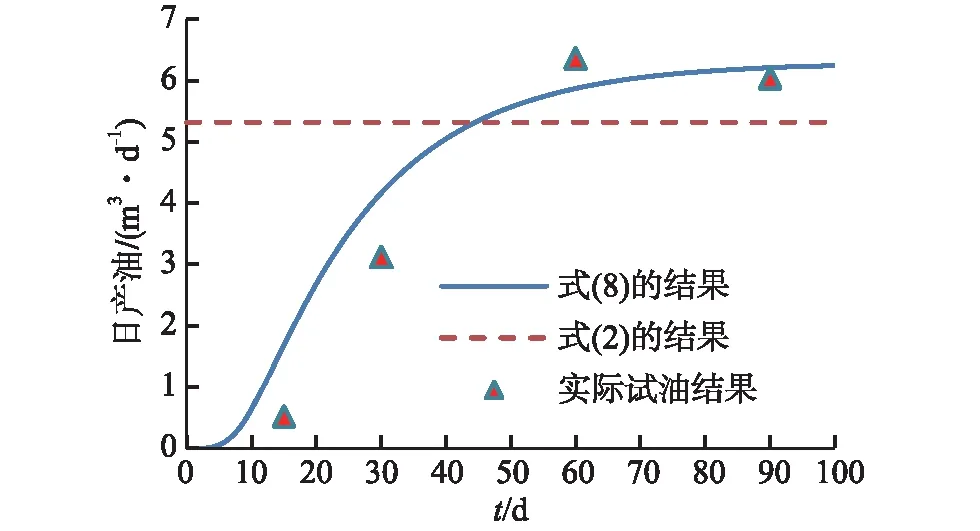
图5　两种方法计算的日产量与实际试油结果的对比图Fig.5 The comparison between day production calculated by capillary pressure formula and by practical production testing

4　结　论

本研究通过求解重力作用下轴对称非稳态渗流压强场方程的解析解,提出了一种径向第一类非齐次边界条件和纵向第二类齐次边界条件下的二维轴对称输运方程的一般求解方法,并获得了如下结论:

1) 注水开采时,地层中的注水压强及注水压强梯度均随深度增大而增大．对于渗透率分布均匀的地层,其底部的渗流速度更快．

2) 随着压强波的传播,地层中的注水压强分布状况逐渐趋于稳定．在该过程中,生产井内的日产量逐渐上升至最大值．

3) 由于地层底部的注水压强梯度较大,因此,如果注水之后还需要通过压裂、酸化等措施提高地层渗透率,则应该优先针对地层顶部实施．

4) 仅在边界条件中考虑了重力的作用,而式(3)本身并未反映重力的影响,今后将针对该问题对式(3)进行改进,并提出新的求解方法．

参考文献：

[1]姚同玉,黄廷章,李继山.孔隙介质中稠油流体非线性渗流方程[J].力学学报,2012,44(1):106-110.

[2]林振生.两类椭圆偏微分方程解的存在性问题[J].福建师范大学学报(自然科学版),2010,4(1):1-33.

[3]沈钦锐,程立新,周宗福.一类三阶多时滞p-Laplacian方程周期解的存在性[J].武汉大学学报(理学版),2013,59(6):505-510.

[4]严绍洋,李亮辉,高燕希,等.公路隧道开挖渗流场的有限差分法分析[J].中外公路,2007,27(6):120-123.

[5]杜泽.基于有限差分计算的某水库大坝渗流场稳定性分析[J].安徽农业科学,2016,44(3):309-311.

[6]杨正明,于荣泽.特低渗透油藏非线性渗流数值模拟[J].石油勘探与开发,2010，37(1):35-37.

[7]周志军.低渗透储层流固耦合渗流理论及应用研究[D].大庆:大庆石油学院,2003:76-82.

[8]刘振宇.有限元法在油藏渗流中的理论和应用[D].大庆:大庆石油学院,2003:44-65.

[9]王君连.用势函数法计算渗流干扰区的地下水流态[J].水利水电技术,1999,30(2):19-25.

[10]张建国,杜殿发,侯健,等.油气层渗流力学[M].2版.北京:中国石油大学出版社,2010:63-67.

[11]同登科,葛家理.分形油藏非达西低速渗流模型及其解[J].大庆石油地质与开发,1996,15(3):18-23.

[12]李宏伟.带启动压力梯度的渗流方程求解[D].长春:东北石油大学,2013:18-21.

[13]邓英尔,刘慈群.低渗油藏非线性渗流规律数学模型及其应用[J].石油学报,2001,22(4):72-77.

[14]廖作才.非线性渗流方程解析方程研究及应用[D].北京:中国科学院渗流力学研究所,2015:15-22.

[15]王晓冬,侯晓春,郝明强,等.低渗透介质有启动压力梯度的非稳态压力分析[J].石油学报,2011,32(5):847-851.

[16]石达友.超稠油油藏水平井产量变化规律研究[D].青岛:中国石油大学(华东),2009:33-42.

[17]梁昆淼.数学物理方法 [M].3版.北京:高等教育出版社,1998:261-263.