一个基于格的环签名方案的改进

热娜·艾合买提,张　娟,李　伟,曾吉文*

(1.厦门大学数学科学学院，福建 厦门 361005；2.新疆师范大学数学科学学院，新疆 乌鲁木齐 830054)

2001年,Rivest等[1]在群签名的基础上提出了环签名.它是一种特殊的群签名,实现了签名者的完全匿名性，被广泛应用于网上投票、电子选举等领域.截止目前,大部分环签名方案本质上都是基于数学中的困难问题假设[2-4]，安全性很大程度上依赖于安全参数的选取[5]．并且,基于离散对数问题的签名无法抵抗量子攻击[6].因此,设计更加安全的环签名方案成为密码学发展的一个重要方向.

一个n维格是Rn上的离散子群,基于格中困难问题(如最短向量问题等)的密码构造可以抵抗量子攻击.Ajtai等[5，7-9]证明了某些格中困难问题在一般情况和最坏情况下的困难性相当.因此,在基于格中困难问题的密码体制中,随机挑选实例[5]与最难实例的安全性相同.这个重要性质是大部分传统的密码体制所不具备的.而且,格中涉及的线性运算和模运算相比传统密码的指数运算速度快.

许多人对基于格的环签名方案进行了研究[10-14].2010年,Cash 等[10]提出了格基派生技术来为用户产生公私钥,并设计了第一个基于格的环签名方案,但是此方案消息扩展较长,不利于实施.2011 年,Wang 等[11]提出一个新的环签名方案,并声称他们的方案可以满足全密钥暴露下的匿名性和内部攻击下的不可伪造性.然而，该方案在内部攻击条件下不满足不可伪造性.本研究改进了Wang的方案：新方案在随机谕言模型下,可以满足全密钥暴露下的匿名性和内部攻击下的不可伪造性；并且使用了Micciancio等[15]提出的一种新的陷门生成算法.由于这种新的陷门生成算法在计算方面简单、有效、容易实施,因此本研究的签名方案和其他方案相比也更高效.

1　预备知识

本文中系统参数为n.对任意一个正整数k,[k] 表示集合{1,2，…，k}.设矩阵A=[a1，a2，…，am],其中ai表示矩阵A的第i个列向量.‖a‖表示a的欧几里得范数，且‖a‖=maxx∈[m]‖ai‖.

1.1　格(Lattice)

一个格是Rn的离散子群,它由Rn中n个线性无关的向量生成,称其为基向量.设B=[b1,b2，…，bn]是n×n矩阵,由n个线性无关的基(列)向量b1,b2，…，bn组成．那么一个由B生成的n维格Λ定义如下:

Λ=L(B)={Bc:c∈Zn}，

在密码应用中,通常将格(基底)限制到Zn上.

Λ⊥(A)={e∈Zm:Ae=0modq}，

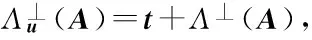
对任何r>0,Rn上中心在c,偏差为r的高斯函数定义如下[8]:

x∈Rn,ρr,c(x)=exp(-π‖x-c‖2/r2).

对任意c∈Rn,r>0及n维格Λ,Λ上的离散高斯分布定义如下:

x∈Λ,DΛ,r,c=ρr,c(x)/ρr,c(Λ)，

其中ρr,c(Λ)=∑xΛρr,c(x)为固定值.

1.2　格中困难问题假设

本研究环签名方案的安全性依赖于格中SIS问题(small integer solution problem)、ISIS 问题(inhomogeneous small integer solution problem)的困难性,定义如下[5]:

1.3　格的基本算法

本文中使用了Micciancio等[15]在2012年提出的一种新的陷门生成算法:

2)A的分布与均匀之间的统计距离可忽略.

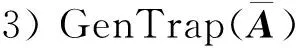
定义域中取原像算法SampleD(A,T,H,u,s):在给定函数值时,可以利用陷门信息取样得到较短的原像[15].

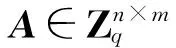
3) SampleD(A,T,u,s)指的是SampleD(A,T,I,u,s).

2)T′的分布与离散高斯分布之间的统计距离可忽略.

3) 随机变换A′的列向量不影响算法的实施.

4) DelTrap(A′,A,T,s′)指的是DelTrap(A′,A,T,I,s′).

2　环签名

2.1　环签名的定义

一个环签名由3个概率多项式时间算法[4]构成:KeyGen,Ringsign,Ringverify.

1) KeyGen(1n):输入安全参数n,该算法为每个成员输出签名密钥ski和验证密钥vki.

2) Ringsign(ski,R,M):输入环R,签名者的私钥ski,消息M∈{0,1}*,该算法输出环R对消息M的签名v.

3) Ringverify(R,M,v):输入环R,消息M及环签名v,如果签名合理,算法回答接受,否则拒绝.

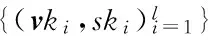
2.2　环签名方案的匿名性

一般的环签名方案抗全密钥暴露下的匿名性证明定义如下:

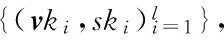
2.3　环签名方案的不可伪造性

一般的环签名方案在内部攻击下不可伪造证明定义如下:

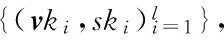
A在上述游戏中取胜的优势定义如下：

3　本研究提出的方案

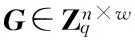
H(·,·):{0,1}*×{0,1}m→{0,1}n.

是一个安全的Bash函数.安全性分析时将视H(·,·)为一个随机器.为了方便起见,令其中的可逆矩阵H=I.

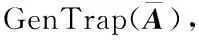
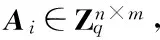
(ii) 利用算法 DelTrap(AR,Ai,Ti,s′) 派生出AR的陷门TR.

(iii) 利用算法 SampleD(AR,TR,y) 取样得到v∈ZLm,显然满足ARv=ymodq.

(iv) 最后输出用户i对消息M的签名v.

3) Ringverify(R,v,M):给定一个环R,消息M,签名v,当下述两个条件满足时,验证者接受这个签名:

(ii)ARv=H(R,M) modq.

否则,验证者不接受．

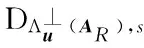
3.1　全密钥暴露下的匿名性

定理1若将H(·,·)视为一个随机谕言模型,假设ISISq,lm是困难的,则本研究的环签名方案在全密钥暴露下是匿名的.

证明假设存在一个自适应的敌手A攻击环签名方案在全密钥暴露下的匿名性,挑战者构造一个多项式时间算法C来响应 A的攻击环境.设A 的询问次数是qE.为了响应A 的询问,存储两个列表H和K,他们在初始状态下都是空的.

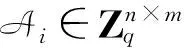
2) 询问阶段:C分别回答A的hash询问、私钥询问及签名询问如下:其中Ri表示环R的含有l个成员的任一子环,Mj为任一消息．

(ii)Ri中用户i1的私钥询问阶段:C查找列表K,返回Ti1给A.

(iii) 询问环Ri中的成员i1对消息Mj的签名〈i1,Ri,Mj〉:可以假设H(Ri,Mj)已经被A询问过了,C查询H列表〈Ri,Mj,yij〉得到yij,执行算法 SampleD得到vij,并将vij返回给A.

A发出挑战〈k0,k1,R*,M*〉,使环R*对消息M*签名,k0,k1是R*中的两个成员.C选择b*←{0,1},检查列表H中元组〈R*,M*,y*〉,运行算法DelTrap得到AR*的陷门TR*,然后计算挑战签名v*← SampleD(AR*,TR*,y*),将v*给A,最终A输出它的猜测b′←{0,1}.

3.2　内部攻击下的不可伪造性

定理2若将H(·,·)视为一个随机谕言模型,假设 SISq,lm是困难的,则本研究的环签名方案在内部攻击下是安全的.

证明假设存在一个自适应的敌手A攻击环签名方案内部攻击下的不可伪造性,挑战者构造一个多项式时间算法C来模拟A的攻击环境,解决SIS问题.设询问次数是qE,A 和C进行如下游戏.为了响应A的询问,C存储两个列表H和K,他们在初始状态下都是空的.

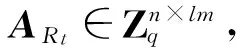
2) 询问阶段:C分别回答A的Hash询问、私钥询问及签名询问如下:其中Ri表示环R的含有l个成员的任一子环,Mj为任一消息．

(i) 对H(Ri,Mj)的Hash询问:C返回一个随机值eij←Zlm,服从高斯分布DZlm,r,返回yij←ARteijmodq给A,然后将(Ri,Mj,eij,yij) 存储在列表中H.

(ii) 对k私钥询问:如果k∉Rt,C在列表K中寻找〈k,Ak,Tk〉,然后将Tk返回给A.否则中止.

(iii)询问环Ri中的成员i1对消息Mj的签名〈i1,Ri,Mj〉:可以假设H(Ri,Mj)已经被A询问,如果Ri=Rt,C查找列表H(Ri,Mj,eij,yij),将eij返回给A.若Ri≠Rt,分两种情况:

情况1:i1∈Ri-Rt,此时〈i1,Ai1,Ti1〉包含在列表K中,那么C运行DelTrap算法获得ARi的陷门TRi←DelTrap(ARi,Ai1,Ti1),检查H列表中的(Ri,Mj,eij,yij),计算挑战签名vij←SampleD(ARi,TRi,yij),并将vij返回给A.

情况2:i1∈Ri∩Rt,C寻找一个i2∈Ri-Rt,使得〈i2,Ai2,Ti2〉包含在列表K中,运行DelTrap算法获得ARi的陷门TRi←DelTrap(ARi,Ai2,Ti2),C重新在列表H中获得(Ri,Mj,eij,yij),然后计算挑战签名vij←SampleD(ARi,TRi,yij) 并将vij返回给A.

3) 挑战阶段,A输出一个伪造〈i*,R*,M*,σ*〉,如果R*≠Rt,C失败,否则C寻找列表H中的〈R*,M*,e*,y*〉,然后输出v=σ*-e*,即为 SIS问题实例fARt的解.

分析:设敌手A输出一个合理的伪造的概率是ε,挑战者C成功解决SIS问题实例主要取决于私钥询问阶段和挑战阶段.

(i)在私钥询问阶段,R中有l个成员的私钥是未知的,被询问到的概率为1/qE,因此询问成功即i∉Rt,C询问成功的概率是1-1/qE.

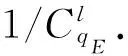
4　结　论

本文中提出的新的环签名方案在随机谕言模型下是可以满足全密钥暴露下的匿名性和内部攻击下的不可伪造性.而且使用一种强陷门生成算法,保证了新的签名方案简单、高效且容易实施.

参考文献：

[1]RIVEST R,SHAMIR A,TAUMAN Y.How to leak a sercret[C]∥Proceedings of the ASIACRYPT 2001.Berlin:Springer-Verlag,2001:552-565.

[2]ZENG S,JIANG S,QIN Z.An efficient conditionally anonymous ring signature in the random oracle model[J].Theoretical Computer Science,2012,461:106-114.

[3]SHIM K A.An efficient ring signature scheme from pai-rings[J].Information Sciences,2015,300:63-69.

[4]BENDER A,KATZ J,MORSELLI R.Ring signatures:stronger definitions,and construction without random oracles[J].Journal of Cryptology,2009,22(1):114-138.

[5]AJTAI M.Generating hard instances of lattice problems (extended abstract)[C]∥STOC.Philadelphia:ACM,1996:99-108

[6]SHOR P W.Polynomial-time algorithms from prime factorization and discrete logarithms on a quantum computer[J].SIAM Journal on Computing,1997,26(5):1484-1509.

[7]DWORK C.A public-key cryptosystem with worst-case and/average-case equivalence[C]∥Proceeding of Twenty-ninth ACM Symposium on Theory of Computing.[S.l.]:ACM,1997:284-293.

[8]MICCIANCIO D,ROSEN O.Worst-case to average-case reductions based on Gaussian measures[J].SIAM Journal on Computing,2007,37:267-302.

[9]ALWEN J,PEIKERT C.Generating shorter bases for hard random lattices[J].Theory of Computing Systems,2011,48 (3):535-553.

[10]CASH D,HOFHEINZ D,KILTZ D,et al.Bonsai trees,or how to delegate a lattices basis[J].Eurocrypt,2010,6110:523-552.

[11]WANG J,SUN B.Ring signature schemes from lattice basis delegation[J].Lecture Notes in Computer Science,2011,7043:15-28.

[12]NOH G,CHUNJ Y,JEONG I R.Strongly unforgeable ring signature scheme from lattices in the standard model[J].Journal of Applied Mathematics,2014(2014):1-12.

[13]GENTRY C,PEIKERT C,VAIKUNTANATHAN V.Trapdoors for hard lattices and new cryptographic constructions[C]∥Proceedings of the 40th Annual ACM Symposium on the Theory of computing(STOC′08).[S.l.]:ACM,2008:197-206.

[14]MELCHOR C A,BETTAIEB S,BOYEN X,et al.Adapting Lyubashevsky′s signature schemes to ring signature setting[J].Progress in Cryptology,2013,7918:1-25.

[15]MICCIANCIO D,PEIKERT C.Trapdoors for lattices:simpler,tighter,faster,smaller[J].Lecture Notes in Computer Science,2012,7237:700-718.