生态移民安置区景观格局的尺度效应分析——以红寺堡区为例

孔福星， 王亚娟,2， 刘小鹏,2， 王 鹏， 陈 晓

(1.宁夏大学 资源环境学院, 银川 750021; 2.宁夏(中阿)旱区资源评价与环境调控重点实验室, 银川 750021)

景观生态学是20世纪60年代兴起的一门新兴学科，它主要研究空间格局、生态学过程与尺度之间的相互关系。随着景观生态学的不断发展，尺度效应成为近20 a景观生态学的研究热点[1-4]。景观生态学的尺度是研究某一物体和现象所采用的空间和时间单位，也可指某一现象或过程在空间和时间所涉及的范围和发生的频率。对于景观生态学的研究来说尺度的选择尤为重要，尺度的选择对景观格局分析结果影响很大。尺度选择过大，往往导致大量细节被忽略；尺度选择过小，就会陷入局部，容易忽略总体规律[5-7]。景观生态学把尺度分为幅度和粒度。查新近年来景观格局尺度的文章，发现对粒度的研究比较多。如韩蓉等[8]研究了粒度变化对玛纳斯河流域土地利用景观格局尺度的影响，发现玛纳斯河流域适宜计算的粒度范围为400～2 000 m。马振刚等[9]研究了化德县农牧交错带地区土地利用的粒度效应,得出10～20 hm2的范围最适宜。陈永林等[10]研究了长沙市土地利用格局变化的空间粒度效应，得出90 m是分析空间粒度的最佳值。研究幅度时可以保持粒度不变，改变研究样本的面积[11]。邬建国等[12]提出两种幅度推绎方法，即由研究区中心向外推绎，采用正方形或圆来划分幅度。或由研究区一角向外推绎，采用正方形划分幅度。这两种方法在之前的研究中得到了广泛应用。在此基础上，岳文泽等[13]借鉴粒度推绎原理提出一种新的幅度推绎方法，即用固定大小的正方形网格与研究区进行叠置，计算每个网格内的景观指数，通过改变网格大小，计算每个幅度下景观指数的空间分布格局。已有极少数学者对此方法进行了研究[14-16]。

生态移民是指将重要生态功能区、生态环境恶劣无法生存地区、生态环境严重破坏的地方的人迁移到环境承载力好的地方，从而实现迁出区可持续发展的一种重要手段[17]。红寺堡1998 年开始安置来自宁夏南部地区的贫困群众，已经成为全国最大的生态移民安置区，移民的不断迁入，使该地景观生态系统遭受到巨大的破坏。文章从尺度方面研究红寺堡在不同幅度下的规律性，探究红寺堡景观研究的最佳尺度，同时为生态移民安置、景观优化等提供借鉴和参考。

1　研究区概况

红寺堡位于毛乌素沙漠边缘，是宁夏中部干旱带的核心区，它由盐池县、同心县、青铜峡市、中宁县、利通区等周边县(市)行政面积调整组合而成。位于东经105°43′45″—106°42′50″，北纬37°28′08″—37°37′23″，现辖2镇3乡，62个行政村，国土总面积2 767 km2，红寺堡地形以坡丘陵为主，平均海拔1 345 m，属中温带干旱气候区，年平均气温在8.4℃，昼夜温差大，降雨量为277 mm，且集中在7—9月，相对湿度达到52%。红寺堡区是宁夏唯一全县域生态移民安置区，也是国内最大的异地生态移民安置区。截至2015年底，全区总人口达197 350人，其中回族人口达62.64%。

2　研究方法

2.1　数据处理方法

本研究以红寺堡区2015年Landsat/TM数据为数据源，分辨率为30 m，有7个波段。将Landsat/TM影像进行波段合成、几何精矫正、裁剪、利用软件ENVI并结合google earth进行解译。遥感影像Kappa系数在0.9以上，并利用野外调查修正初步解译图中的的错误图斑，最终得到研究区2015年的土地利用矢量数据。

首先利用ArcGIS的格网索引要素生成(1 km×1 km，2 km×2 km，3 km×3 km，4 km×4 km，5 km×5 km)的网格，用每个网格切割红寺堡区2015年景观矢量图。1 km×1 km生成了2 975张矢量图，2 km×2 km生成了797张矢量图，3 km×3 km生成了372张矢量图，4 km×4 km生成了224张矢量图，5 km×5 km生成了152张矢量图。将切割出来的矢量图转成栅格图，矢量转栅格时，栅格大小固定为30 m。利用Fragstats 3.4软件计算每张栅格图的景观指数。这样在不同幅度下每个网格中都有一个景观指数值，将每个网格的值赋给网格的中心点。并将结果导入GS+(美国Gamma Design Software)，利用半变异函数分析不同幅度下景观指数的空间异质性和空间依赖性，根据半变异函数的拟合效果分析出红寺堡的最佳幅度。最后利用ArcGIS地统计分析模块中的普通克里金插值(Ordinary Kriging)，绘制不同幅度下2015年红寺堡景观多样性指数和斑块密度的空间分布图。

2.2　半变异函数计算

半变异函数(又称半方差分析或变异距分析)是地统计学中的一种分析方法，它是关于数据点的变异值和数据点距离的函数，它弥补了地统计学中没有考虑观测值空间位置的欠缺[18-19]，可以表示为：

(1)

半变异函数γ(h)是一个单调递增函数，当h=0时，γ(0)=CO，CO称为块金值，它表示随机部分引起的空间异质性。随着h的增大，γ(h)单调递增，当h超过某个值后，γ(h)不再继续增加，而是成为一个相对平稳的值，这个值称为基台值CO+C，变异函数达到基台值时的h称为变程AO，反映了数据空间自相关的极限距离。基台值和块金值的差值C表示空间自相关引起的空间异质性。CO/(CO+C)则反映了随机因素引起的空间异质性占总空间异质性的比重[20]，如果比值<25%，说明系统空间相关性很强，如果比例在25%～75%，表明系统空间相关性中等；若>75%说明系统空间相关性很弱[21-22]。

回归系数r2和残差RSS是评价函数模拟效果的两个指标，r2越大，RSS越小，则拟合效果越好。

2.3　景观指数的选取

研究表明，斑块密度指数和景观多样性指数对幅度变化有明显的响应，因此文章选取了这两个指标来进行研究。

2.3.1斑块密度指数斑块密度(PD)表示单位面积景观的斑块数，斑块密度反映了景观的被分割的破碎化程度，同时也反映了在人类的影响下，景观空间异质性的程度。PD越大，破碎化的程度越高[23]，其计算公式如下：

(2)

式中：N为景观中总的斑块数；A为景观总面积(m2);PD为斑块密度(个/km2)。PD>0，无上限，并受到栅格大小的限制，当每一个栅格代表一个独立的斑块时，PD取得最大值。

2.3.2Shannon多样性指数景观多样性指数反映一个区域内，景观类型的均匀化和复杂化程度[24-25]。多样性指数的大小与不同景观类型所占的面积百分比和景观类型数目两个因素有关。如在一个研究区内，土地利用程度越高，破碎化程度越高，计算出的SHDI越大，如果整个景观中只有一个斑块，SHDI=0。

(3)

式中:Pi为i类景观的面积占景观总面积的比例;m为景观类型总数。该指标取值范围，SHDI≥0，无上限。

3　结果与分析

3.1　研究区景观的基本特征

研究区7种土地利用类型面积中最大是草地，面积为1 932.756 km2，占总面积的比例为70.632%；其次为耕地和林地，面积分别为14.203%和7.049%；其他景观类型面积都比较小，均未超过总面积的10%。建设用地，未利用地，沙地，水域，其面积分别为105.571 km2，59.429 km2，34.597 km2，22.489 km2，占总面积的比例分别为3.858%，2.172%，1.264%，0.822%(表1)。

3.2　幅度变化对景观指数空间变异性的影响

3.2.1景观多样性指数通过ArcGIS计算1 km，2 km，3 km，4 km，5 km幅度下SHDI的Moran′I，发现Moran′I值分别为0.624 8，0.614 3，0.620 3，0.574 8，0.527 7，说明5个幅度下SHDI都存在空间自相关。不同幅度下景观多样性指数随着幅度的变化具有一定程度的相似性，在假设各向同性的前提下，得到不同幅度下的景观多样性变异函数的函数及参数。

表1　各类型景观面积及所占的比例

多样性指数的大小与各景观类型占研究区总面积的比例和景观类型数目两个因素有关。当幅度太小时，如果斑块面积太大，大于一个网格的面积。那么可能出现一个网格里面只有一个斑块，使得很多网格的景观多样性指数为0。当幅度增加时，一个网格内的斑块数相应增加。景观多样性还与研究区景观类型的分布以及破碎度有关。从表2可知，各个幅度下多样性指数的参数是有区别的，最优拟合模型均为指数模型。

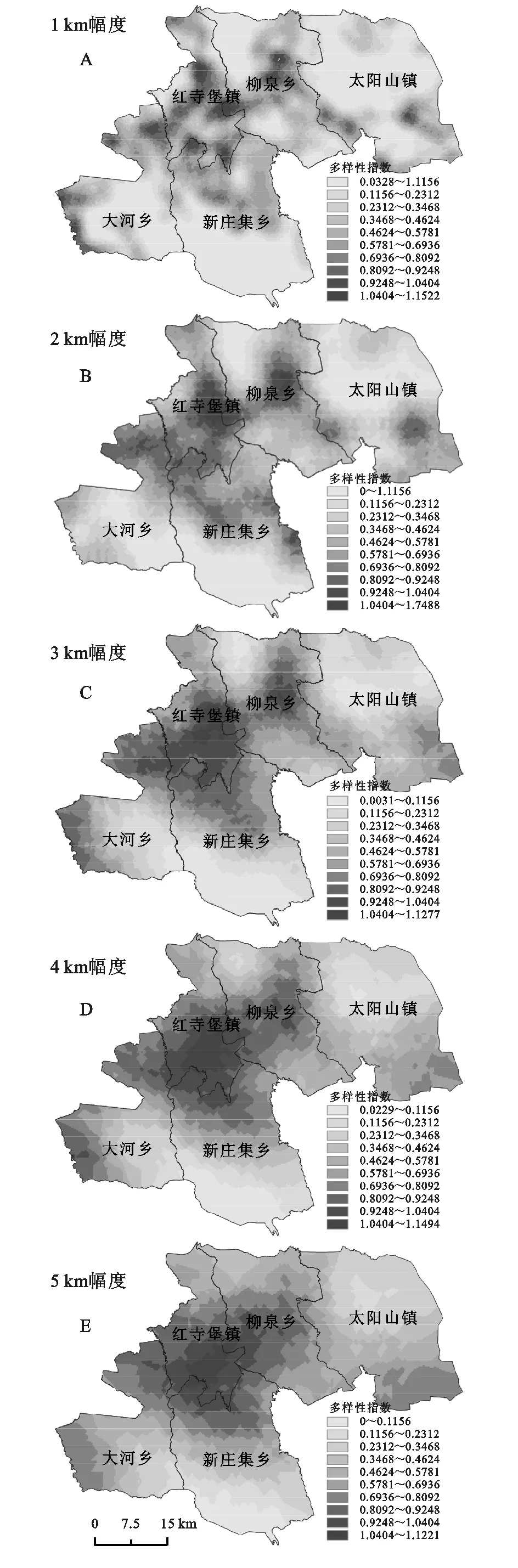
在1 km幅度下，块金值CO为0.046 8，基台值CO+C为0.154 6，块金值与基台值的比率CO/CO+C为0.302 7，其反映景观多样性指数的空间异质性有69.73%是空间自相关贡献的，而有30.27%是由随机因素贡献的；在2 km幅度下，块金值CO为0.031 4，基台值CO+C为0.187 8，块金值与基台值的比率CO/CO+C为0.167 2，其反映景观多样性指数有16.72%是由随机因素贡献的；在3 km幅度下，块金值为0.030 7，基台值CO+C为0.201 4，块金值与基台值的比率CO/CO+C为0.288 4；4 km幅度下，块金值CO为0.033 1，基台值CO+C为0.220 5，块金与基台值的比率CO/CO+C为0.150 1；5 km幅度下，块金值CO为0.022 1，基台值CO+C为0.208 2，块金与基台值的比率CO/CO+C为0.106 1。1 km幅度下25%

从1 km到5 km随着幅度的增加，变程加大，说明多样性指数在更大范围内都存在着空间依赖性。从1 km到5 km块金与基台的比值CO/CO+C逐渐减小。按照半变异函数的理论，当幅度加大时，半变异函数的块金值不断增加，块金效应也增强。但是根据拟合结果，3 km幅度下的块金值CO比1 km和2 km幅度下的块金值CO小，说明1 km和2 km幅度对于研究区来说太小，破坏了景观的整体结构。5 km幅度下，块金值比较小，块金与基台值的比率也比较小，表明在样本数目较少的情况下，较小范围的变异逐渐被忽略，系统空间相关性增强。综合红寺堡的土地利用状况以及半变异函数模拟效果，文章认为3 km幅度是比较合适的尺度。

表2　不同幅度下景观多样性半变异函数的参数

3.2.2斑块密度指数计算1 km，2 km，3 km，4 km，5 km幅度下PD的Moran′I，分别为0.079 2，0.067 9，0.034 9，0.044 0，0.005 7，说明5个幅度下PD的Moran′I，存在空间自相关。在2 km幅度下，拟合模型为高斯模型，其他幅度下拟合效果均为指数模型。景观斑块密度指数在不同幅度下半变异函数的参数见表3。

在1 km幅度下块金值CO为8.79，基台值CO+C为27.71，块金值和基台值的比例CO/CO+C为0.317 2，说明斑块密度指数的空间异质性有31.72%是由随机因素提供的，有68.28%是由空间自相关部分提供的。在2 km幅度下块金值CO为68.062 1，基台值CO+C为325.5，块金值和基台值的比例CO/CO+C为0.209 1。3 km幅度下，块金值CO为2.05，基台值CO+C为9.845，块金值和基台值的比例为0.208 2。4 km幅度下，块金值为0.15，基台值为7.309，块金值和基台值的比例CO为0.020 5。5 km幅度下，块金值为0.111 4，基台值为6.629，块金值和基台值的比例CO/CO+C为0.016 8。1 km幅度下25%

1 km和2 km幅度下，块金值较大，表明在较小尺度内空间变异程度较大。从2 km到5 km，变程都比较大，说明多样性指数在更大范围内都存在着空间依赖性。从1 km幅度到5 km幅度，块金值和基台值的比例CO/CO+C也逐渐减小，表示随机部分引起的空间异质性占总的空间异质性比例减小，空间自相关引起的空间异质性占总的空间异质性比例增加。

当幅度较小时，一个网格可能只有一个或几个少数的斑块，那么斑块密度程度必然较低。较小的尺度显示了更细微的变异。当幅度增加时，掩盖了小尺度的变异，显示了整体的变化，尺度过大就会损失太多信息。因此考虑模拟效果和样本数量，3 km是红寺堡比较合适的尺度。

表3　不同幅度下斑块密度半变异函数的参数

3.3　幅度变化对景观指数的空间格局的影响

3.3.1多样性指数

(1) 在1 km幅度下，景观多样性指数空间格局细节变化较多，呈现圈层分布。由于草地和耕地是大片分布的，被幅度分割的网格面积小于斑块面积时，该幅度只存在一种景观类型，则多样性指数就为0。总体来说，草地分布较广的区域景观类型单一，多样性指数较低。耕地广布的区域，人口分布较多，景观类型也丰富，多样性指数较高(图1A)。

(2) 在2 km幅度下，景观多样性指数空间格局非常复杂，各高值中心从内到外依次显示高值—低值—高值—低值。几个高值中心出现在红寺堡镇中部，太阳山镇东南部，柳泉乡中部、新庄集乡中部和东南部。这些区域都是在人口分布集中，工业发达的地区(这些区域汇聚了宁夏弘德包装材料有限公司、中国石化、渔光湖旅游区、宁夏绿苑公司，居民区以及相应的配套设施)，属于城市化快速发展时期，土地改造强度大，自然景观被严重破化，有多种土地利用类型，斑块破碎化程度比较高。几个低值中心分布在大河乡中部，新庄集乡南部，太阳山镇中部、柳泉乡西北部，这些区域人口较少，大面积草地分布，土地利用类型比较单一，大部分地区只有草地这一种土地利用类型(图1B)。

(3) 在3 km幅度下，景观多样性指数空间格局已经没那么复杂，两个主要的高值中心(红寺堡镇和柳泉乡中心)还在，太阳山镇东南部和新庄集乡西南部的高值中心发生了转移。和2 km幅度相比，在大河乡西部增加了一个高值中心，几个低值中心的位置没有发生明显转移。这时，红寺堡区中部地区和周边地区的空间格局差异更明显的突显出来了(图1C)。

(4) 在4 km幅度下，景观多样性指数的空间格局更加简单，这时更加明显的表现为城市开发带和未开发或开发程度较低地带的区别。由红寺堡中部向南，向北和向西逐渐减小，向东依次显示高值—低值—高值—低值。太阳山镇东南部的高值中心又发生了转移，总体趋势为逐渐向东南部移动，大河乡西部的高值中心未发生明显转移，几个低值中心仍未发生转移(图1D)。

(5) 5 km幅度下多样性指数的空间分布格局和4 km幅度差距不大。除太阳山镇南部多样性增加外，其他区域无明显变化(图1E)。

从1 km到5 km，各个幅度下的空间格局发生了显著的变化。随着幅度的增加，被网格分割的面积之间增大，多样性程度也相应增加，不过还要考虑景观类型和破碎化特征。尺度较小时能揭示更多的细节特征，尺度增加时，细节特征逐渐被掩盖，大尺度变异特征凸显。

3.3.2斑块密度指数由斑块密度指数的公式1可知在斑块数等同的条件下，网格中的研究区面积越小，PD越大。在研究PD时，在同一幅度下必须保证每个网格中所占有的研究区面积是一样大的。对研究区进行网格分割时，研究区外围网格中的样本面积小于网格面积，因此外围这些网格没有研究意义。因此，文章在对PD进行克里金插值时，剔除了外围斑块面积不完整的网格，只对剩余的网格进行空间插值。

(1) 在1 km幅度下，斑块密度指数的空间分布较为复杂。景观类型较单一，景观连续性好，破碎度低的区域，斑块密度就小。斑块密度较低的地方主要以草地为主。主要位于大河乡和新庄乡交界处、太阳山镇中部、柳泉乡西北部、新庄集乡南部、新庄集乡和太阳山镇交界处。斑块密度较高的区域，主要位于经济较发达，人口分布集中的区域。高值中心较多，空间变异特征明显(图2A)。

(2) 在2 km幅度下呈现较为明显的圈层分布。有5个较明显的高值中心，分别位于红寺堡镇中部、柳泉乡中部、太阳山镇东南部、大河乡和红寺堡镇交界的地方、新庄集乡东南部。几个高值中心由内到外依次为高值—低值—高值—低值。在聚落发展过程中，会逐渐向外围扩大，对土地需求大，土地会被切割成各种类型，土地破碎化程度高，斑块数量就多。除了新庄集乡东南部这个高值中心外，其他高值中心都在人口比较集中，工农业都比较发达的地区。新庄集乡东南部的那个高值中心和其他几个高值中心不同的是，它不是在经济发达的地区，它位于罗山自然保护区，森林广布。出现高值的原因在于，森林斑块破碎，斑块数量较多。和1 km幅度相比，几个低值中心未发生明显转移(图2B)。

(3) 在3 km幅度下，斑块密度指数的空间分布趋于简单，总体趋势没有变，但是最高值中心发生了转移。在2 km幅度下，最高值出现在罗山保护区，在3 km幅度下最高值出现在红寺堡镇中部。有两个高值中心，红寺堡镇中部和柳泉乡中部，高值中心从内到外逐渐减小。红寺堡镇是红寺堡区的经济中心，交通发达，人口居住密集，土地被切割的最破碎，因此相同面积内的斑块数也最多，斑块密度也最大。柳泉乡镇也是一个新崛起经济发力镇，耕地分布较广，人口密集，配套设施齐全，土地破碎，因此斑块密度也较大。几个低值中心没有发生明显转移。这时候更加突出的表现为经济发达地区与周边欠发达地区的区别(图2C)。

(4) 在4 km幅度下，斑块密度指数的空间分布更加趋于简单，而且圈层边界更加光滑。和3 km幅度相比，大河乡西部、新庄集乡中部、太阳山镇西南部和东南部这些小的高值中心更加凸显出来了。几个低值中心依旧没有发生转移(图2D)。

(5) 5 km幅度下，斑块密度的空间分布和4 km幅度趋同，没有太大差别。不同幅度下，斑块密度指数的空间分布也不同。小幅度破坏了斑块原有的空间形状，误差比较大，在图上会出现一些突变。比如在2 km幅度下，罗山附近的高值区，在3 km，4 km和5 km的空间分布图中并没有出现(图2E)。

图1　不同幅度下景观多样性的空间格局

图2　不同幅度下斑块密度的空间格局

4　结 论

(1) 随着幅度的增加，多样性指数的空间格局发生了变化；个别高值中心发生了转移，低值中心未发生明显转移；多样化程度增加。不同幅度下，多样性指数的最高值都出现在市中心。斑块密度指数的空间格局也发生了变化；高值中心发生了转移，由于1 km和2 km幅度的尺度太小，空间分布图上差异性较大；低值中心没有发生转移。

(2) 景观多样性指数和斑块密度指数和人类活动有关。市区景观类型多样，破碎度大。人类活动较少的区域，景观比较连续，多样性小，破碎度低。小幅度下，景观指数的空间变异最复杂。随着幅度增加，景观指数的空间分布趋于简单，局部细节逐渐被掩盖，宏观变化逐渐凸显。

(3) 半变异函数揭示了景观指数的空间变异特征。总体来看，随机因素在总空间变异所占比重较小，空间自相关所占比重较大。随着幅度增加，块金值与基台值的比值逐渐减小，说明说明随机部分引起的空间异质性不断减弱,而空间自相关造成的空间异质性不断加强。

(4) 对于红寺堡来说1 km和2 km幅度的尺度太小，使得总体规律被局部规律所掩盖。4 km和5 km幅度太大，损失了太多空间格局规律信息。综合考虑样本数量、研究区面积和半变异函数的拟合效果，认为3 km幅度是研究红寺堡景观格局比较合适的幅度。

(5) 景观多样性指数和斑块密度指数具有尺度依赖性，不同幅度下得到的结果差异很大，因此在景观生态学的研究中绝不能忽视尺度对景观格局的影响。

参考文献：

[1]殷小彤.西北地区农村居民点景观格局指数的尺度效应及其最佳粒度选择分析:以西安市为例[J].中国农业资源与区划,2016，37(12):149-154.

[2]Wu J. Hierarchy and scag: Extrapolating information along a scalinling ladder[J]. Canadian Journal of Remote Sensing, 1999,25(4):367-380.

[3]Lu Y, Fu B. Ecological scale and scaling[J]. Acta Ecologica Sinica, 2001,21(12):2096-2105.

[4]陈利顶,李秀珍,傅伯杰,等.中国景观生态学发展历程与未来研究重点[J].生态学报,2014，34(12):3129-3141.

[5]Levin S A. The problem of pattern and scale in ecology[J]. Ecology, 1992,73(6):277-326.

[6]刘媛媛,刘学录.甘肃永登县土地利用景观格局的空间尺度效应[J].应用生态学报,2016，27(4):1221-1228.

[7]李双成,蔡运龙.地理尺度转换若干问题的初步探讨[J].地理研究,2005，24(1):11-18.

[8]韩蓉,唐湘玲.玛纳斯河流域近14年多尺度粒度变化对土地利用景观格局的影响[J].水土保持研究,2017，24(2):194-201.

[9]马振刚,李黎黎,许学工,等.北方农牧交错带地区土地利用的粒度效应研究:以化德县为例[J].干旱区资源与环境,2016，30(5):92-98.

[10]陈永林,谢炳庚,李晓青.长沙市土地利用格局变化的空间粒度效应[J].地理科学,2016，36(4):564-570.

[11]刘铁冬,许大为.景观生态学案例分析：河流景观格局与生态脆弱性评价[M].北京:科学出版社,2015.

[12]邬建国.景观生态学：格局、过程、尺度与等级[M].北京:高等教育出版社,2007.

[13]岳文泽,徐建华,徐丽华.基于遥感影像的城市土地利用生态环境效应研究:以城市热环境和植被指数为例[J].生态学报,2006，26(5):1450-1460.

[14]杜秀敏,黄义雄,叶功富.厦门市景观格局的尺度效应分析[J].测绘科学,2010，35(4):71-73.

[15]杨晓玲.江苏东台围垦区景观格局变化及其尺度效应研究[D].南京:南京师范大学,2011.

[16]杜秀敏.厦门市景观格局尺度效应与形成机制研究[D].福州:福建师范大学,2009.

[17]杨显明,米文宝,齐拓野,等.宁夏生态移民效益评价研究[J].干旱区资源与环境,2013，27(4):16-23.

[18]卫春阳,徐丹丹,董凯凯,等.遥感影像空间格局变异函数分析研究进展[J].地球信息科学学报,2017，19(4):540-548.

[19]张涛,吴剑锋,林锦,等.变异函数模型对渗透系数克里格插值的影响研究[J].水文地质工程地质,2016，43(4):1-7.

[20]王政权.地统计学及在生态学中的应用[M].北京:科学出版社,1999.

[21]董立宽,方斌.茶园土壤重金属乡镇尺度下空间异质性分析:以江浙优质名茶种植园为例[J].地理研究,2017，36(2):391-404.

[22]魏阳,丁建丽,王飞,等.新疆玛纳斯流域非农业种植地盐碱性空间变异特征[J].生态学报,2016，36(23):7655-7666.

[23]郑新奇,付梅臣.景观格局空间分析技术及应用[M].北京:科学出版社,2010.

[24]徐新良,庞治国,于信芳.土地利用、覆被变化时空信息分析方法及应用[M].北京:科学技术文献出版社,2014.

[25]何东进.景观生态学[M].北京:中国林业出版社,2013.