非持续连通通信拓扑下的多导弹协同制导

叶鹏鹏， 盛安冬， 张蛟， 武兆斌， 戚国庆， 李银伢

(1.南京理工大学 自动化学院, 江苏 南京 210094; 2. 63961部队, 北京 100012)

0　引言

随着现代导弹防御体系能力的提升，单一导弹突防已难以获得较为满意的打击效果[1]。为提高导弹的打击能力、增加毁伤概率、实现对目标的齐射攻击，近年来许多学者对多导弹协同制导问题进行了研究[2-7]。

在多导弹协同制导问题中，各导弹同时到达目标即获得相同的遭遇时间是重点研究的问题之一。文献[8]针对固定或者慢速移动目标提出了一种遭遇时间可控(ITCG)的制导律，在经典比例导引(PNG)法的基础上加入遭遇时间误差反馈修正，实现了反舰导弹的遭遇时间可控制导。文献[9]提出了一种双层协同制导结构，底层使用ITCG制导律进行导引，上层采用协调一致算法，以实现对制导时间指令的解算。文献[10]提出了一种二段式协同制导方法，第一阶段各枚导弹通过信息交互实现弹目距离以及前置角的一致，第二阶段各导弹独立导引至目标。文献[11]在文献[10]的基础上重点研究了各枚导弹遭遇时间的一致性策略，通过反馈线性化方法将非线性制导问题转换为线性一致性问题，使得分析更加简单。文献[12]在考虑遭遇时间一致的基础上加入末端攻击角约束，运用模型预测扩张控制和协同比例制导设计了一种协同次优制导律。

以上关于多导弹协同制导律的设计，均假设各枚导弹之间的通信处于理想条件下，即实际通信链路拓扑固定。然而导弹在长途飞行过程中极有可能因为复杂的战场环境使通信受到干扰，从而造成通信丢包，同时由信息传输引起的随机时延也无法避免。因此，在设计多导弹协同制导律时，必须考虑时变拓扑对多导弹协同的影响。文献[13]考虑拓扑不确定以及存在通信时延条件下的多导弹协同制导问题，通过实现制导时间分歧系统的渐近稳定保证了多导弹协同制导遭遇时间一致。文献[14]考虑了通信拓扑存在跳变和时延情况下的领从拓扑结构多导弹协同制导问题，将领从一致性问题转换成误差系统的稳定性问题，通过反馈线性化方法获得制导律。

上述研究中虽然通信拓扑是时变的，但是要求任意时刻导弹间的通信拓扑均为连通的，由于通信丢包与时延的存在，导致导弹间的实际通信拓扑随机变化，可能出现某一时刻导弹间通信拓扑不连通甚至导弹间通信中断的情况，因此文献[13-14]中所提多导弹协同制导方法并不能直接用于存在通信丢包情形下的多导弹协同制导问题。

本文研究了针对固定目标的多导弹协同制导问题，所提制导方法分为两个阶段。第一阶段为协同制导阶段，各导弹经过信息交互实现协调变量的一致。为解决协同制导过程中导弹通信拓扑由于丢包和时延而随机变化、导致拓扑非连通甚至通信中断等问题，首先将丢包过程描述成伯努利分布，并引入一种时延处理机制，从而得到实际通信拓扑随机出现的概率；其次将导弹相关协调变量线性化，构造协调变量误差系统，借助多体一致性等相关理论证明了实现误差系统的稳定等效于实现协调变量的状态一致，并给出了为实现协同制导而选取控制器增益的依据。第二阶段为独立导引阶段，各导弹在实现协调变量的一致状态且接近目标后，断开通信链路连接，独立导引至目标。采取两阶段制导方法有利于降低通信干扰对协同制导的影响，也有利于实现对目标的静默攻击，增加导弹突防能力，提高毁伤概率。最后，通过仿真示例对所提制导方法进行了验证。

由于在实际工程中导弹的制导指令都是在离散状态下设计的，本文中各枚导弹以固定周期进行通信，这种对连续时间模型的离散化采样，使得多导弹的协同制导问题更加复杂，但却对实际工程应用具有直接指导意义。此类基于通信采样数据实现一致性的问题，在多智能体领域得到了大量研究[15-17]，然而在多导弹协同制导领域，此类研究成果尚非常有限。本文重点关注的是存在丢包及时延情况下通信拓扑非持续连通对协同制导的影响，因此侧重研究了第一阶段即协同制导阶段各导弹的制导策略。

1　问题描述

1.1　通信拓扑描述

本文中的通信拓扑用无向图g(V,ε,A)表示，简记为g，其中：V={1,2,…,N}表示各导弹节点；ε⊆V×V表示通信链路；A=[aij]N×N为邻接矩阵，aij=1表示导弹j向导弹i传输信息，此时j处于i的邻域中，记为j∈Ni(t)，aij=0表示无通信。无向图中A是对称的，即aij=aji. 拉普拉斯矩阵定义为L=[lij]N×N，式中：

(1)

无向图是连通的，是指图中任意两个节点都可以直接或者间接通信；无向图集的并图是指由集合中所有图的节点与边所组成的联合图。

1.2　链路丢包及时延处理机制

假设1导弹通信链路是双向的，且各链路相互独立；通信链路丢包过程满足伯努利分布；在信息成功传输的前提下，由传输引起的时延满足均匀分布。

记导弹i与导弹j之间的链路丢包概率以及链路最大时延分别为αij和dij，记链路成功通信的概率为βij，βij=Pr (aij=1)，其中aij为拓扑邻接矩阵A中的元素，则可得

βij=(1-αij)(min {dij,τ}/dij).

(2)

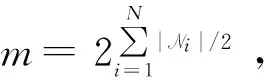
(3)

1.3　导引几何关系

三维空间的导引问题可以解耦成纵向平面和横侧向面的导引问题。本文主要考虑仅由气动力控制导弹在二维纵向平面针对固定目标的制导问题。设定导弹为质点模型，轴向速度大小不变，仅通过改变导弹的法向过载来实现导引。

导引几何关系如图1所示，其中：T表示目标，Mi表示导弹i；ri、vi和ai分别表示导弹i的弹目距离、轴向速度以及法向过载，ai垂直于导弹的轴向方向；ϑi、θi分别表示导弹i的视线角和弹道倾角。

导弹i的动力学方程可表示为

(4)

(5)

(6)

实际工程中，最常用的制导方法为PNG法[11]，制导律如(7)式所示，其中kn∈[3,6]为比例系数常数。

(7)

(8)

记导弹i的控制输入为

(9)

则导弹i的动力学方程可表示为

(10)

1.4　协同制导

如图2所示，由N枚导弹组成的多导弹系统对目标进行齐射攻击，由于导弹的初始状态(弹目距离、弹道倾角、导弹速度等)不同，若不加修正，则无法保证导弹到达目标的遭遇时间一致。因此本文设计一种协同制导律，各枚导弹利用交互信息自主产生制导指令，调整自身弹道倾角，使得各枚导弹同时到达目标。需要说明的是，图2中的虚线为导弹的飞行示意轨迹，表示导弹最终同时到达了目标。

当任意导弹i与导弹j满足(11)式时，各枚导弹的遭遇时间与前置角一致，此时多导弹系统便实现了协同制导。

(11)

式中：E(·)表示数学期望值。

如(11)式所示，与基本一致性定义中协调变量的差值渐近收敛于0不同，本文寻求的是保证协调变量差值的数学期望值收敛于0，即均值意义下的一致。由于通信链路中存在丢包和随机时延等现象，实际的通信拓扑为随机的，若无特殊说明，下文中的渐近一致均是指均值意义下的一致。

(12)

因此，(11)式可以改写为(13)式：

(13)

2　协同制导律设计

2.1　控制律设计

设计一种线性协同控制律如(14)式所示：

(14)

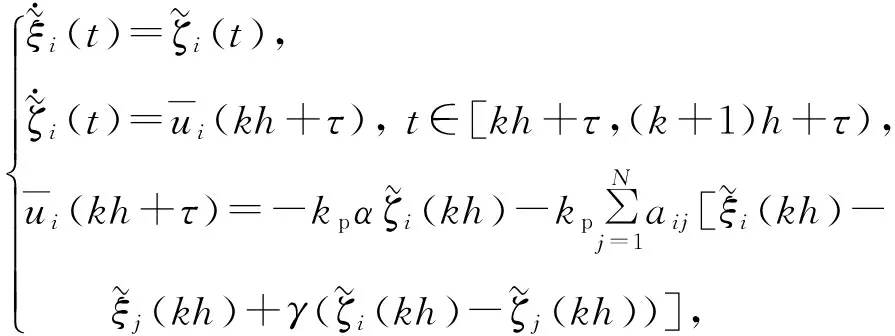
(15)

2.2　收敛分析

(16)

(16)式表示导弹飞行过程中相关状态误差的变化过程，其中G(k)为误差系统状态转移矩阵：

(17)

式中：IN-1为N-1阶单位矩阵；矩阵Ψ(·)和Γ(·)的定义分别为

(18)

(19)

(20)

对(16)式两边求数学期望，得

(21)

从而可得如下定理。

证明必要性。当ρ(Ω)≥1时，(21)式无法收敛，即导弹在其飞行过程中的相关变量误差无法收敛至0值，因此导弹协同变量无法达到一致。

充分性。当ρ(Ω)<1时，由矩阵理论可知，存在一个范数‖·‖*，使得‖Ω‖*=η<1，η为一正常数。对(21)式两边求取范数，得

(22)

(23)

则有

定理1表明了实现(21)式的稳定等效于协调变量达到渐近一致状态，从而实现协同制导。当(21)式稳定后，各枚导弹的遭遇时间与前置角一致，且前置角渐近收敛于参考值。因此，如何选取控制器增益，即确定协同控制律中相关参数的设计依据，使得误差系统稳定，是实现多导弹协同制导的关键。

2.3　控制参数设计

将Gi分解，得到Gi=F-ΞiR，其中：

因此，

(24)

式中：Ω的特征多项式为

(25)

fi(s)=s3-s2((2-hkpα)-λic1)+
s((1-hkpα)+λic2)-λic3，

(26)

其中，

(27)

定理2通信链路存在丢包和时延时，多枚导弹在协同控制律(14)式作用下实现协同制导的充要条件是拓扑集合{g1,g2,…,gm}的并图是连通的，且满足如下条件：

(28)

充分性。由引理1可知，拓扑集合{g1,g2,…,gm}的并图为连通图时，λi>0(i=1,2,…,N-1)。

对(26)式进行双线性变换，令s=(q+1)/(q-1)，得

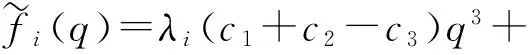
(2hkpα+λi(c1-c2+3c3))q2+

(4-λi(c1+c2+3c3))q+

(4-2hkpα+λi(c2+c3-c1)).

(29)

则(25)式的根位于单元圆内，等价于(29)式的根位于左半平面。根据劳斯判据，可知：

(30)

将(27)式代入(30)式，得

(31)

经过相关计算，得(28)式中的条件。因此，当拓扑集合的并图是连通的，且满足(28)式中的各项条件时ρ(Ω)<1，由定理1可知，多导弹系统实现了协同制导。证毕。

理论上，当控制增益kp、α、γ的选取满足定理2中的条件时，只要时间充足，多导弹系统始终能实现协同制导。然而在实际工程中，控制增益的选取必须考虑两点重要因素：一是导弹实际过载能力，二是各导弹至目标的遭遇时间。若控制增益选取得过小，则导弹间相关变量误差收敛较慢，造成导弹已经到达目标但协调变量还没有达到一致，即各枚导弹不能同时到达目标；若控制增益选取得过大，则得到的过载指令超出了导弹过载能力，此时指令无意义。

2.4　法向过载

定理1和定理2给出了多导弹实现协同制导的充要条件，而实现多导弹系统协同制导策略需给出各导弹的法向过载。对(9)式、(12)式进行相关运算，得

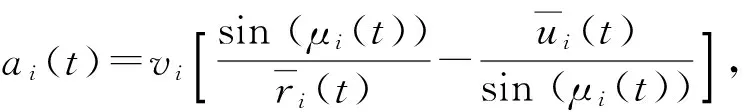
(32)

在协同制导阶段，各导弹的过载指令由(32)式产生，协调变量达到一致且接近目标后进入第二阶段，即独立导引阶段，各导弹采用PNG法，过载指令由(7)式产生，独立导引至目标。

3　仿真实验

考虑4枚导弹M1、M2、M3和M4协同制导，实现对固定目标T的打击。导弹初始状态如表1所示，目标T坐标为原点(0,0)，导弹间的理想通信链路拓扑无向图如图3所示，图中连线表示导弹间可以双向通信，取ζr=-0.999. 假设导弹在其飞行过程中速度大小始终不变，产生的制导指令为法向过载，从而改变导弹的弹道倾角。参考工程中的实际相关技术性能指标，对如下两种通信情形下的多导弹协同制导系统进行数值仿真。

表1　导弹初始状态表Tab.1　Initial states of missiles

情形1当t∈[0 s,170 s)时，通信链路的通信间隔h为0.1 s，丢包概率为0.1，各链路的最大传输时延为0.09 s，设置时间阈值τ为0.05 s. 因此可能会出现8种通信链路拓扑，各拓扑出现的概率相等，为0.125，且可知8种通信链路拓扑集合的并图是连通的。根据定理2中的各条件要求，选取控制器增益kp=0.1，α=1，γ=5，则ρ(Ω)=0.987 7<1. 当t≥170 s时，各导弹相关状态达到一致并已接近目标，此时采用PNG制导律独立导引至目标，比例参数kn=3.

仿真结果如图4～图6所示。图4(a)、图4(b)分别为协同制导阶段4枚导弹的协调变量ξi(t)、ζi(t)-ζr的变化示意图，图中4枚导弹的协调变量渐近一致，且ζi(t)渐近收敛于ζr(图4(b)中ζi(t)-ζr渐近趋向0)，此时各导弹的遭遇时间与前置角渐近一致，且前置角收敛于参考值；当t≥170 s时，各导弹采用比例制导独立导引至目标。完整的制导过程中4枚导弹的弹目距离如图5所示，导弹弹道如图6所示。由图5和图6可知，4枚导弹在t≈188 s时可以同时到达目标，实现齐射攻击，且具有良好的弹道特性。

图7显示了多导弹系统协同制导阶段各时刻的实际通信次数。由图3可知，实际通信拓扑为连通的，当且仅当该通信时刻多导弹间的通信次数为6，而当某一时刻通信次数为0时，表示该时刻所有通信中断。由图7可知，协同制导阶段导弹间的实际通信拓扑并非持续连通的，且多次出现通信中断的情况。

情形2导弹初始状态、通信拓扑与情形1相同，当t∈[0 s,160 s)时，通信链路的通信间隔h为1.0 s,丢包概率为0.1，各链路最大传输时延为0.9 s，设置时间阈值τ为0.5 s. 根据定理2中的各条件要求，选取控制增益为kp=0.05，α=2，γ=10，此时ρ(Ω)=0.910 9<1. 当t≥160 s时，各导弹相关状态达到一致并已接近目标，此时采用PNG制导律独立导引至目标，比例参数kn=3.

仿真结果如图8～图10所示，其中，图8(a)、图8(b)为协同制导阶段4枚导弹协调变量变化示意图，图9为完整制导过程中4枚导弹的弹目距离变化情况，图10为4枚导弹的弹道图。由图8(a)、图8(b)可知，4枚导弹的遭遇时间与前置角渐近一致，且前置角渐近收敛至参考值。由图9和图10可知，4枚导弹同时到达目标，且弹道特性良好。

图11显示了多导弹系统协同制导阶段各时刻的实际通信次数，同样，实际的通信拓扑并非持续连通的。

图12为各导弹在协同制导阶段施加的过载指令变化示意图。由于通信拓扑在任一通信时刻都会发生随机切换，且无法保证拓扑的连通性，由图11中对通信次数的统计可知，通信拓扑处于连通时的概率较低。因此在导弹整个协同制导阶段，各导弹过载会产生波动，从而造成飞行轨迹并非光滑曲线。尤其在协同制导的初始阶段(0～20 s)，各导弹的相关协调变量一致性误差较大，在这种较差的通信情况下各导弹过载出现多处峰值，此过程中需要导弹具有较高的过载机动能力。

在实际应用中，若导弹间通信条件较差而造成要求导弹具有较高的过载机动能力，可从两个方面进行改进以适应制导要求：1)增强导弹的过载机动能力，考虑到一般气动力布局的导弹过载能力有限，可在导弹的横侧向安装反作用喷气控制系统，以提高导弹的实际过载能力；2)对于本文中存在丢包及时延的协同制导情形，可以通过增大时延处理机制的时延阈值来提高导弹实际通信成功概率，从而确保过载变化更加平稳。如情形2中，原有的时延阈值为0.5 s，任一通信链路通信成功的概率只有0.5. 将导弹时延阈值设为0.9 s时，任一通信链路实际通信成功的概率为0.9，此时协同制导阶段的各导弹过载变化如图13所示。与图12相比，在协同制导阶段的初始阶段，各导弹的过载变化较为平缓，即不会出现图12中多处峰值的情况，并且过载更快地收敛于0，此种情况下各导弹的弹道更平直，其飞行轨迹如图14所示。

由于在导弹飞行过程中通信存在随机丢包和时延，通信拓扑可能在任一通信时刻随机切换，当导弹间实际通信成功的概率较低时，对导弹的过载机动能力要求较高；当导弹间实际通信成功的概率较高时，则可放低对导弹的过载机动能力要求。与现有的研究成果要求通信拓扑持续连通相比，本文中导弹通信处于一种较为恶劣的条件下，其通信拓扑可能随机切换，且在通信过程中无法保证连通性，甚至出现多次通信中断的情形，因此对过载机动能力要求相对较高。

情形1与情形2分别对通信间隔为0.1 s和1.0 s的多导弹协同制导系统进行了仿真验证，理论分析与仿真示例均说明了两种情形下的多导弹系统能够实现协同制导。理论上，对于任意的通信间隔，只要选择合适的时延阈值和控制器增益，本文所提的制导方法均能使多导弹系统协调变量渐近一致。然而，当通信间隔选取过大时，可能出现当导弹的遭遇时间减至0即已经到达目标时，多导弹系统的相关协调变量尚未获得一致状态，因此不能实现齐射攻击；当通信间隔选取过小时，除了对导弹通信链路带宽提出更高要求外，由于通信丢包与随机时延的出现，多导弹系统的一致性输入将会频繁切换，此时对导弹机动和过载能力又进一步提出了要求。

因此，必须首先根据导弹初始状态，尤其需要重点考虑各导弹的初始遭遇时间，确定合适的通信间隔，然后根据导弹机动、过载能力选择合适的控制增益，并且必须满足定理2条件，当各枚导弹的相关协调变量获得一致且足够接近目标后，各导弹采用PNG法独立导引至目标。

4　结论

针对多导弹协同制导中实际通信拓扑并非持续连通问题，本文提出了一种只利用通信采样数据实现制导的分布式协同制导方法。理论分析与仿真验证结果均表明，在某一时刻实际通信拓扑非连通甚至所有通信中断的情况下，该制导方法能够确保各枚导弹的遭遇时间一致，从而达到对目标的齐射攻击，实现多导弹系统的协同制导。

本文所提的协同制导算法考虑了实际应用中导弹通信能力以及所受通信环境的影响，可为多导弹穿越复杂战场环境时的协同导引律设计提供参考。如何在通信拓扑随机切换时保证导弹过载不会突变、实现过载的平缓变化，对工程应用具有重要意义，也是未来研究工作主要考虑的方向。

参考文献(References)

[1]关世义. 飞航导弹突防技术与战术导论[J]. 战术导弹技术, 2006(4):1-8.

GUAN Shi-yi. Introduction to penetration technologies and tactics for aerodynamic missile[J]. Tactical Missile Technology, 2006(4):1-8. (in Chinese)

[2]赵启伦，陈建，李清东，等. 高超武器和常规导弹协同攻击策略可行域研究[J]. 航空学报，2015，36(7)：2291-2300.

ZHAO Qi-lun, CHEN Jian, LI Qing-dong, et al. Feasible region of hypersonic and ballistic missiles’ cooperative attack strategy[J]. Acta Aeronautica et Astronautica Sinica, 2015, 36(7): 2291-2300. (in Chinese)

[3]赵建博，杨树兴. 多导弹协同制导研究综述[J]. 航空学报，2017，38(1):020256-1-020256-13.

ZHAO Jian-bo, YANG Shu-xing. Review of multi-missile cooperative guidance[J]. Acta Aeronautica et Astronautica Sinica, 2017, 38(1): 020256-1-020256-13. (in Chinese)

[4]王昊宇，徐学强，房玉军.网络化协同打击弹药技术[J].兵工学报，2010，31(2):136-139.

WANG Hao-yu, XU Xue-qiang, FANG Yu-jun. Networked cooperative attack ammunition technology[J]. Acta Armamentarii, 2010, 31(2):136-139. (in Chinese)

[5]施广慧, 赵瑞星, 田加林, 等. 多导弹协同制导方法分类综述[J]. 飞航导弹, 2017 (1): 85-90.

SHI Guang-hui, ZHAO Rui-xing, TIAN Jia-lin, et al. Review of classified method of multi-missile cooperative guidance[J]. Winged Missiles Journal, 2017 (1):85-90. (in Chinese)

[6]曾家有，王国卫，钟建林，等. 多平台舰舰导弹饱和攻击几个协同问题与模型[J]. 兵工学报, 2014, 35(2):256-261.

ZENG Jia-you, WANG Guo-wei, ZHONG Jian-lin, et al. Research on cooperative saturation attack problems and models of ship-to-ship missiles from multi-ship platforms [J]. Acta Armamentarii, 2014, 35(2):256-261. (in Chinese)

[7]赵启伦，陈建，董希旺，等. 拦截高超声速目标的异类导弹协同制导律研究[J]. 航空学报，2016，37(3):936-948.

ZHAO Qi-lun, CHEN Jian, DONG Xi-wang, et al. Cooperative guidance law for heterogeneous missiles intercepting hypersonic weapon[J]. Acta Aeronautica et Astronautica Sinica, 2016,37(3):936-948. (in Chinese)

[8]Jeon I S， Lee J I， Tahk M J． Impact-time-control guidance law for anti-ship missiles[J]．IEEE Transactions on Control Systems Technology, 2006, 14(2): 260-266．

[9]赵世钰，周锐. 基于协调变量的多导弹协同制导[J]. 航空学报，2008，29(6): 1605-1611．

ZHAO Shi-yu, ZHOU Rui. Multi-missile cooperative guidance using coordination variables[J]. Acta Aeronautica et Astronautica Sinica, 2008，29(6): 1605-1611. (in Chinese)

[10]Wang Y J, Dong S, Ou L L, et al. Cooperative control of multi-missile systems[J]. IET Control Theory and Applications, 2014, 9(3): 441-446.

[11]Zhao Q L, Dong X W, CHEN J, et al. Distributed cooperative guidance for multiple missiles[C]∥Proceedings of the 2016 35th Chinese Control Conference (CCC). Chengdu, China: IEEE, 2016: 5346-5351.

[12]李新三，汪立新，王明建，等．基于MPSC和CPN制导方法的协同制导律[J].北京航空航天大学学报, 2016,42(9):1857-1863．

LI Xin-san, WANG Li-xin, WANG Ming-jian, et al. Cooperative guidance law based on MPSC and CPN guidance method[J]. Journal of Beijing University of Aeronautics and Astronautics, 2016 , 42(9): 1857-1863. (in Chinese)

[13]王青, 后德龙, 李君, 等. 存在时延和拓扑不确定的多弹分散化协同制导时间一致性分析[J]. 兵工学报, 2014, 35(7): 982-989.

WANG Qing, HOU De-long, LI Jun, et al. Consensus analysis of multi-missile decentralized cooperative guidance time with time-delays and topology uncertainty[J]. Acta Armamentarii, 2014, 35(7): 982-989. (in Chinese)

[14]Sun X J, Zhou R, Hou D L, et al. Consensus of leader-followers system of multi-missile with time-delays and switching topologies[J]. Optik, 2014, 125(3): 1202-1208.

[15]Zhang Y, Tian Y P. Consensus of data-sampled multi-agent systems with random communication delay and packet loss[J]. IEEE Transactions on Automatic Control, 2010, 55(4): 939-943.

[16]Cheng L, Wang Y P, Hou Z G, et al. Sampled-data based average consensus of second-order integral multi-agent systems: switching topologies and communication noises[J]. Automatica, 2013, 49(5): 1458-1464.

[17]Han G S, He D X, Guan Z H, et al. Multi-consensus of multi-agent systems with various intelligences using switched impulsive protocols[J]. Information Sciences, 2016, 34(9): 188-198.

[18]Guan Z H, Liu Z W, Feng G, et al. Impulsive consensus algorithms for second-order multi-agent networks with sampled information[J]. Automatica, 2012, 48(7): 1397-1404.