事件触发容积卡尔曼滤波及其在火控探测网络中的应用
梁苑, 盛安冬, 武兆斌, 张蛟, 戚国庆, 李银伢
(1.南京理工大学 自动化学院, 江苏 南京 210094; 2.63961部队, 北京 100012)
0 引言
多传感器融合估计广泛应用于目标跟踪、导航定位、区域监视等领域。其中,基于非线性滤波的融合方法可更好地处理非线性系统中的估计问题,受到越来越多的研究与关注。
对于高维非线性系统,容积卡尔曼滤波(CKF)[1]的估计精度优于无迹卡尔曼滤波[2],已得到大量研究与应用[3-4]。Arasaratnam[5]基于信息滤波器形式下的平方根CKF(SCKF)研究了集中式传感器网络中的融合问题。刘华等[6]提出了基于SCKF的集中式序贯融合算法。丁家琳等[7]针对分布式传感器网络提出了基于SCKF的一致滤波算法,其中各节点在每个融合周期内通过若干次交互及迭代信息贡献矩阵,以达到估计结果的平均一致。为提高各节点估计结果的精度和达到一致的速度,Liu等[8]提出基于SCKF的一致滤波算法,其中各节点额外交互了自身得到的先验估计值。
上述基于CKF的融合算法中,传感器到融合中心以及传感器间的数据传输均是周期性的,可称之为周期传输机制。数据传输消耗的能量是传感器能耗的主要部分之一[9],周期传输机制可能会导致数据传输过于频繁,从而带来较大的通信消耗。事件触发机制通过预设的触发准则选择性传输数据,在减小通信消耗的同时可在一定范围内保证系统的估计精度。针对集中式网络,Battistelli等[10]研究了基于卡尔曼滤波的事件触发融合算法。针对分布式网络,Liu等[11]和Li等[12]分别提出了交互量测和交互局部估计值的事件触发融合算法。针对非线性系统,Li等[13]研究了事件触发无迹卡尔曼滤波算法。然而,基于CKF的事件触发融合算法仍然有待研究。
此外,在实际系统中,探测设备故障、高噪声工作环境等因素可能导致不完全量测的出现,而上述文献所设计的事件触发机制均未考虑不完全量测的影响。另一方面,量测向量中各分量多由不同的测量设备获取,而已有的文献[14-15]在处理不完全量测时将量测向量视为一个整体进行判断,可能导致正常的量测分量被舍弃。虽然文献[16]对各量测分量是否传输分别予以判断,但未考虑不完全量测的干扰。
基于以上分析,为减小存在不完全量测的传感器网络中的通信消耗,并尽可能保证估计精度,本文建立了多通道解耦量测方程,设计了多通道解耦的基于双重判断准则的事件触发机制,进而给出了相应的事件触发SCKF融合估计算法,并将所提的事件触发SCKF应用于一种典型火控探测网络,结果表明了所提方法的有效性。
1 问题描述
在笛卡尔坐标系下,目标运动方程为
Xk=f(Xk-1)+wk-1,
(1)
式中:Xk∈nX为k时刻目标在笛卡尔坐标系下的状态向量,nX表示nX维实数空间,nX为Xk的维数;f(·)为状态转移函数;wk∈nX为过程噪声,且wk~(0,Qk),即wk服从均值为0、方差为Qk的正态分布。
以文献[14]为例,当存在不完全量测时,已有的文献通常将系统量测方程描述为
yk=dkCkXk+vk,
(2)
式中:yk为量测向量;dk=1表示量测正常,dk=0表示出现不完全量测;Ck为量测矩阵;vk为量测噪声。由(2)式可见,当出现不完全量测时,量测向量yk中的所有分量均未被利用。
实际系统中,量测向量中的各分量多由不同的探测设备获取。以典型光电探测单元——目标坐标测定仪为例,距离信息由激光测距机获取,角度信息由云台码盘值叠加目标图像中心与白光电荷耦合元件(CCD)/红外热像仪镜头光轴的偏差量获取,即距离信息与角度信息可视为由彼此独立的测量通道获取。
因此,在不完全量测存在的情形下,由N个探测单元构成的集中式传感器网络跟踪(1)式所示的目标时,不失一般性,探测单元i的量测方程可描述为
(3)
式中:yk,i∈ny为探测单元i在k时刻获取的量测向量,ny为yk,i的维数和分别为yk,i中的距离量测分量和角度量测分量,和分别为和的维数和分别表示k时刻目标在以探测单元i所在位置为原点的球极坐标系下的距离信息和角度信息为距离量测噪声,为距离量测噪声的方差角度量测噪声,为角度量测噪声的方差为服从伯努利分布的二元随机变量,即
为减小传感器网络中的通信消耗,使用事件触发机制控制各探测单元到融合中心的数据传输。利用事件触发机制的集中式传感器网络如图1所示。
在各采样时刻,探测单元利用事件触发机制对各测量通道当前所获取的量测数据进行判断,决定是否将数据传输至融合中心。
2 基于双重判断准则的事件触发机制
已有文献[10-13]中的事件触发机制通过判断量测的重要程度(对估计精度的影响程度)是否超过预设的阈值来决定是否传输当前量测数据。以文献[13]为例,其中事件触发机制如下:
(4)
式中:γk=1表示k时刻事件被触发,量测yk被传输,γk=0则相反;k|k-1为yk的先验估计值;δ为触发阈值。
如(4)式所示的事件触发机制正常工作前提为

(5)
基于上述分析,为减小不完全量测的干扰,对探测单元i的测量通道j设计事件触发机制如下:
(6)
与(4)式所示的事件触发机制相比,(6)式所示的事件触发机制中增加了对量测信息有效性的判断;此外,探测单元不同测量通道的探测情况是互不相关的,为避免舍弃有效量测分量,对获取自不同测量通道的量测分量分别予以判断,因而可称之为多通道解耦基于双重判断准则的事件触发机制。
定理1当目标运动方程和各探测单元的量测方程分别如(1)式和(3)式所示时,若使用(6)式所示的事件触发机制控制各探测单元到融合中心的数据传输,则k时刻融合中心可从探测单元i的测量通道j(j=a,b)获取的量测信息为
(7)
(8)
式中:σ→∞;I为维数适当的单位矩阵。

(9)

针对探测单元i的测量通道j,构建虚拟量测方程如下:
(10)
(11)
由于两个互不相关随机变量之和的PDF等于两个随机变量各自PDF的卷积,可得
(12)
由(11)式和(12)式可得
(13)
根据贝叶斯公式可得
(14)
将(13)式代入(14)式,可得
(15)
(16)
由(10)式,此时相应的虚拟量测噪声协方差为

(17)

(18)
3 基于事件触发SCKF的融合估计
以激光测距机和精密测角设备构成的目标坐标测定仪为例,在极坐标系下获取的目标量测与笛卡尔坐标系下的目标状态呈强非线性关系,因此适宜采用非线性估计方法。下面给出基于(6)式所示事件触发机制的事件触发SCKF融合估计算法。
定义1若A∈m×n(m≥n)为列满秩矩阵,则Tria(A)表示对A进行正交分解后所得上三角矩阵的转置矩阵。
当使用(6)式所示事件触发机制控制各探测单元到融合中心的量测数据传输时,相应的事件触发SCKF(DET-SCKF)融合估计算法的运行步骤如下。
3.1 时间更新
依次执行以下各步骤。
(19)
(20)
(21)
式中:Qk-1为上一时刻的过程噪声方差;Chol(Qk-1)表示用平方根法对Qk-1进行分解所得的矩阵;
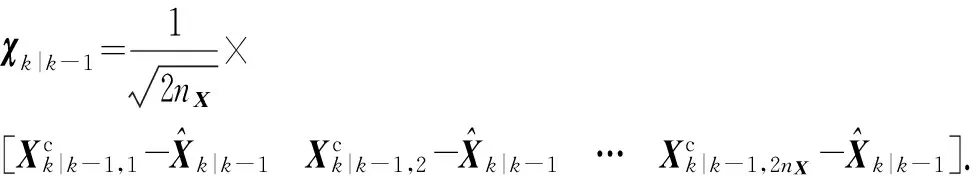
3.2 量测更新
首先执行如下初始化:
3.2.1根据探测情况进行相应设定
根据k时刻探测单元i的距离测量通道和角度测量通道的探测情况进行如下设定。
若i 3.2.2利用量测更新估计结果 利用探测单元i的量测信息Yk,i更新第i-1次循环中得到的目标状态估计值k|k,i-1和误差协方差的平方根因子即依次执行以下步骤。 1) 计算经量测函数传递后的容积点Zk|k-1,l, (22) 2) 计算量测Yk,i的先验估计值k|k-1,i, (23) (24) (25) 5) 计算滤波增益, (26) 6) 利用探测单元i在当前时刻获取的量测信息Yk,i计算目标状态Xk的估计值k|k,i, k|k,i=k|k,i-1+Gk,i(Yk,i-k|k-1,i). (27) (28) 式中: 8) 若i=N,则k时刻融合中心得到的估计结果为 循环结束,返回3.1节,等待k+1时刻继续执行滤波。 为验证本文所提方法的有效性,参考文献[1]中的数值算例进行仿真实验,以比较本文所提方法与已有方法的优劣。 考虑由6个探测单元及1个融合中心构成的集中式传感器网络跟踪在二维平面内进行转弯机动的目标,其运动方程可描述为 各探测单元的量测方程为 估计精度通过均方根误差(RMSE)衡量,位置RMSE和速度RMSE分别为 进一步可定义位置的累积RMSE(ARMSE)和速度ARMSE分别为 式中:K为单次Monte Carlo仿真中的采样周期数。 传感器网络k时刻的平均数据传输量定义如下: (29) (30) 在所有量测均正常的情形下进行仿真实验。设定目标的初始状态如下: X0= 仿真时间为50 s,Monte Carlo仿真次数为500次。 4.2.1DET-SCKF与周期传输SCKF的对比 为说明本文所提方法在减小数据传输量方面的作用,将DET-SCKF与文献[1]中周期传输机制下的SCKF(PT-SCKF)融合估计算法进行对比。 由上述仿真结果可知,本文DET-SCKF与文献[1]中的PT-SCKF相比,位置ARMSE增加幅度为5. 46%,速度ARMSE 增加幅度为4. 40%,平均总数据传输量下降幅度为48. 33%. 性能指标DET-SCKFPT-SCKFΠp/m3.092.93Πv/(m·s-1)7.837.50ρ/次310600 4.2.2DET-SCKF与已有事件触发融合算法的对比 为说明本文所提方法在估计精度方面的优势,将本文的DET-SCKF与文献[10]中的事件触发卡尔曼滤波(ET-KF)算法以及文献[13]中的事件触发无迹卡尔曼滤波(ET-UKF)算法进行比较。 DET-SCKF中的参数设置与上文一致;分别调整ET-KF和ET-UKF的触发阈值,以使得3种方法的数据传输量基本一致。仿真结果如图4、图5和表2所示。 性能指标DET-SCKFET-UKFET-KFΠp/m3.023.123.18Πv/(m·s-1)7.907.957.99ρ/次312313313 由上述仿真结果可知,在数据传输量基本一致的情况下, DET-SCKF与ET-KF以及ET-UKF相比,位置ARMSE减小幅度分别为5.03%和3.21%,速度ARMSE减小幅度分别为1.13%和0.63%. 在不完全量测存在的情形下进行仿真实验。设定目标的初始状态如下: X0= 仿真时间为50 s,Monte Carlo仿真次数为500次。 4.3.1DET-SCKF与已有事件触发融合算法的对比 由上述结果可知,与量测完全正常时相比,DET-SCKF的位置ARMSE增加幅度为2.65%,速度ARMSE增加幅度为1.01%,平均总数据传输量增加幅度为4.81%,说明本文所提方法可有效减小不完全量测的干扰。ET-UKF、ET-KF和PT-SCKF由于缺少对量测有效性的判断机制,估计精度均严重下降。而且ET-UKF和ET-KF的平均总数据传输量已接近PT-SCKF,说明ET-UKF和ET-KF中的事件触发机制已无法正常工作。 表3 DET-SCKF、ET-UKF、ET-KF和PT-SCKF的 ARMSE及平均总数据传输量对比Tab.3 Comparison of ARMSEs and ρ of DET-SCKF, ET-UKF, ET-KF and PT-SCKF 4.3.2本文方法与多通道耦合判断机制的对比 如(6)式所示,本文方法将量测向量中获取自不同测量设备的量测分量有效性分别予以判断,可称之为多通道解耦的判断机制。而已有方法[14-15]在处理不完全量测时将量测向量视为一个整体。基于已有的方法可给出多通道耦合的判断机制如下: (31) 性能指标多通道解耦判断机制多通道耦合判断机制Πp/m3.203.32Πv/(m·s-1)8.008.14ρ/次382383 由上述仿真结果可知,在数据传输量基本一致情况下,与已有的方法相比,本文所提方法可使位置ARMSE减小3.61%、速度ARMSE减小1.72%. 说明存在不完全量测时,将获取自不同测量通道的量测分量有效性分别予以判断,可更有效利用量测信息。 由1部连指挥计算机及4部光电探测单元构成的火控探测网络如图10所示。由图10可见:在该网络中,各光电探测单元获取目标信息并传输至连指挥计算机;连指挥计算机融合接收到的量测数据来引导下属火力打击单元。 火控探测网络中各光电探测单元的量测方程可描述为 式中: 目标标准航迹由靶场光电经纬仪等高精度计量设备提供。目标标准航迹和火控探测网络输出的融合航迹投影图如图11所示。以标准航迹为基准值,融合航迹在笛卡尔坐标系下的误差如图12所示。各融合时刻,光电探测单元到连指挥计算机的数据传输次数如图13所示。 由上述结果可得,在图10所示的火控探测网络中使用本文提出的事件触发SCKF融合估计算法,可减少各光电探测单元到连指挥计算机的数据传输量,同时融合航迹的精度依然满足要求。 为降低传感器网络中各探测单元到融合中心的数据传输量,本文设计了基于双重判断准则的事件触发机制,给出了相应的事件触发SCKF融合估计算法。数值算例结果表明:本文方法与PT-SCKF方法相比,可在减小数据传输量的同时在一定范围内保证系统估计精度;与已有的事件触发融合估计算法相比,可在数据传输量基本一致情况下获得更高的估计精度。试验结果进一步表明了本文所提的事件触发SCKF算法适合于工程应用。 参考文献(References) [1]Arasaratnam I, Haykin S. Cubature Kalman filters[J]. IEEE Transactions on Automatic Control, 2009, 54(6):1254-1269. [2]孙枫, 唐李军. Cubature卡尔曼滤波与Unscented卡尔曼滤波估计精度比较[J]. 控制与决策,2013,28(2):303-308. SUN Feng, TANG Li-jun. Estimation precision comparison of cubature Kalman filter and unscented Kalman filter[J]. Control and Decision, 2013, 28(2):303-308. (in Chinese) [3]王俭臣, 齐晓慧. 基于气动参数辨识的飞控系统传感器故障估计[J]. 兵工学报, 2015, 36(1):103-110. WANG Jian-chen, QI Xiao-hui. Sensor fault estimation method for flight control systems based on aerodynamic parameter identification[J]. Acta Armamentarii, 2015, 36(1):103-110. (in Chinese) [4]黄湘远, 汤霞清, 武萌, 等. 基于5阶降维平方根- 容积卡尔曼滤波的动基座对准应用研究[J]. 兵工学报, 2016, 37(2):219-225. HUANG Xiang-yuan, TANG Xia-qing, WU Meng, et al. Research on initial alignment of moving base with 5th-degree dimensionality reduction SR-CKF[J]. Acta Armamentarii, 2016, 37(2):219-225. (in Chinese) [5]Arasaratnam I. Sensor fusion with square-root cubature information filtering[J]. Intelligent Control and Automation, 2013, 4(1):11-17. [6]刘华, 吴文, 王世元. 基于平方根CKF 的多传感器序贯式融合跟踪算法[J]. 系统工程与电子技术, 2015, 37(7):1494-1498. LIU Hua, WU Wen, WANG Shi-yuan. Multi-sensor sequential fusion tracking algorithm based on square-root cubature Kalman filter[J]. Systems Engineering and Electronics, 2015, 37(7):1494-1498. (in Chinese) [7]丁家琳, 肖建, 张勇. 基于CKF的分布式滤波算法及其在目标跟踪中的应用[J]. 控制与决策, 2015, 30(2): 296-302. DING Jia-lin, XIAO Jian, ZHANG Yong. Distributed algorithm-based CKF and its applications to target tracking[J]. Control and Decision, 2015, 30(2):296-302. (in Chinese) [8]Liu Y, He You, Wang H P. Squared-root cubature information consensus filter for non-linear decentralized state estimation in sensor networks[J]. IET Radar, Sonar and Navigation, 2014, 8(8):931-938. [9]Gungor V C, Hancke G P. Industrial wireless sensor networks: challenges, design principles, and technical approaches[J]. IEEE Transactions on Industrial Electronics, 2009, 56(10):4258-4265. [10]Battistelli G, Benavoli A, Chisci L. Data-driven communication for state estimation with sensor networks[J]. Automatica, 2012, 48(5):926-935. [11]Liu Q Y, Wang Z D, He X, et al. Event-based recursive distributed filtering over wireless sensor networks[J]. IEEE Transactions on Automatic Control, 2015, 60(9): 2470-2475. [12]Li W L, Jia Y M, Du J P. Event-triggered Kalman consensus filter over sensor networks[J]. IET Control Theory & Applications, 2016, 10(1):103-110. [13]Li L, Yu D D, Xia Y Q, et al. Event-triggered UKF for nonlinear dynamic systems with packet dropout[J]. International Journal of Robust and Nonlinear Control, 2017, 27(18):4208-4226. [14]Wang Z D, Daniel W C H, Liu X H. Variance-constrained filtering for uncertain stochastic systems with missing measurements[J]. IEEE Transactions on Automatic Control, 2003, 48(7):1254-1258. [15]Li W L, Jia Y M, Du J P. Distributed Kalman consensus filter with intermittent observations[J]. Journal of the Franklin Institute, 2015, 352(9):3764-3781. [16]陈烨, 李银伢, 戚国庆, 等. 多通道解耦事件触发机制及其在光电传感网络中的应用[J]. 自动化学报, 2017, 43(2):227-237. CHEN Ye, LI Yin-ya, QI Guo-qing, et al. A multi-channel decoupled event triggered transmission mechanism and its application to optic-electric sensor network[J]. Acta Automatica Sinica, 2017, 43(2):227-237. (in Chinese)

4 数值算例
4.1 算例描述


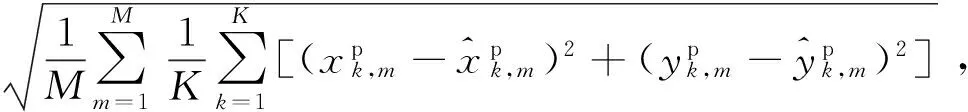
4.2 所有量测均正常时的情形
[1 000 m300 m/s1 000 m0 m/s-3°/s]T,

4.3 存在不完全量测时的情形
[1 000 m300 m/s1 000 m0 m/s-3°/s]T,
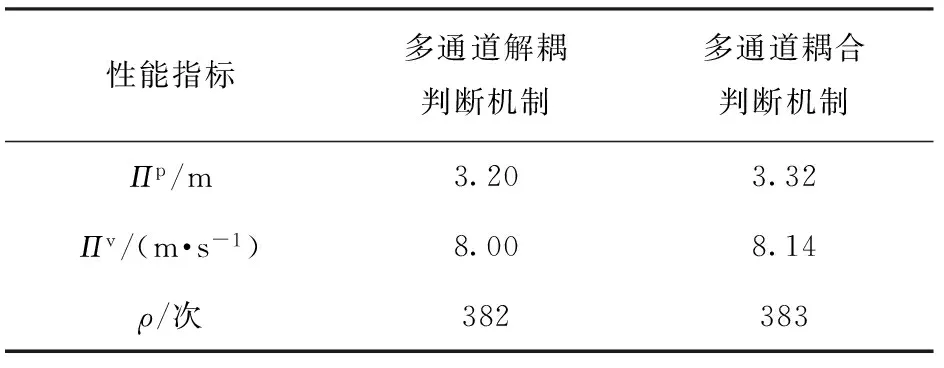
5 事件触发SCKF融合估计算法在火控探测网络中的应用

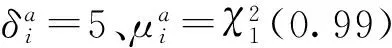
6 结论

