设定源同步采样差异的滞后补偿研究

朱明伟，王进宇，任 炜，杨长林

（1.云南百通电子有限公司，昆明 650000；2.红云红河集团昆明卷烟厂，昆明 650000）

0 引言

随着多轴同步控制系统技术的发展，主轴实现方式从硬件虚拟主轴发展到软件虚拟主轴。同步总线技术出现前，通常采用硬件虚拟主轴；同步总线技术出现后，流行采用软件虚拟主轴。如图1所示。

图1中，硬件虚拟主轴把设定速度转换成连续平滑速度变化过程，再转换成方波编码器信号输出到从轴；软件虚拟主轴用函数直接把设定速度转换成同步位置增量，通过同步总线送达从轴。

随着从轴数量的增多，硬件虚拟主轴及结构的布线量成倍增长，系统复杂度和硬件费用大幅增加。显然，软件虚拟主轴及结构的优点在对比中更加突出。虽然硬件虚拟主轴及结构逐步被软件虚拟主轴及结构取代，但在硬件虚拟主轴及结构中，研究同步时段对设定源的采样导致的设定源采样滞后补偿问题仍然具有理论和应用价值。

1 分析建模

在图1所示的硬件虚拟主轴及结构中，设从轴1的同步时段为t1，从轴2的同步时段为t2，其余从轴的同步时段为t3，且t3=3t1，t2=2t1。把硬件虚拟主轴输出的连续平滑非线性速度变化过程简化为线性变化过程。则简化分析模型如图2所示。

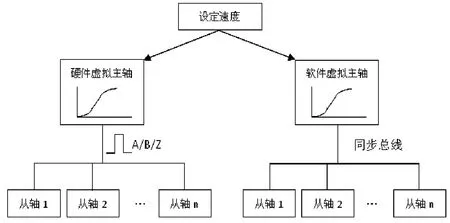
图1 软硬件虚拟主轴及结构对比示意图

图2中，每个小方块的面积代表主轴线性速度变化过程中，以t1为同步时段采样得到的主轴速度在t1时段内产生的同步位移s1=v1×t1。显然存在表1的设定源同步采样与同步位移统计规律。

表1说明：1）在多轴同步控制系统中，同步时段小的轴，对同步设定源先采样先计算输出先产生轴位移。2）主轴速度变化越平缓，同步位移s1越小。3）设同步时段成倍比关系，即某轴同步时段t=n×t1，则该轴与同步时段最小的轴1间因同步时段设定源采样导致的同步位移差△St=(n-1)×t1×v1+(n-2)×t1×v1+…+t1×v1。整理得式⑴。

在图2中，设同步时段t1的轴设定源采样的加速度为A=v1/t1，代入式⑴得到同步位移差△St与同步时段倍长系数n和加速度为A的关系算式(2)。

图2 设定源同步采样滞后与位移分析模型

式(2)说明：在多轴同步控制系统中，设定源加速度A≠0是同步时段长的轴设定源采样滞后造成同步设定位移差△St的主要原因。换言之，为确保硬件虚拟主轴及结构中各从轴与设定源主轴的位移同步，在加速或减速阶段，同步时段长的轴相对于同步时段最短的轴应进行同步设定位移补偿。这种同步设定位移补偿是通过叠加同步设定补偿加速度a实现的。

设同步设定补偿加速度a作用t=n×t1的时间产生的位移等于式(2)计算的同步设定位移差△St，则推导的a与A的关系如下：

式(3)说明：设定源同步补偿加速度a随同步时段倍长系数n的增加而增加，并且小于A。对于多轴同步控制系统的位移同步，为确保较高的同步位移过程控制精度，主轴同步加速度A和同步时段倍长系数n的应用取值存在应用边界的约束。精度要求越高，A值越小，主轴速度变化过程越平缓；n越小（≥1的整数），同步补偿加速度a越小，补偿扰动越小，补偿越易实现。

2 应用边界

在伺服控制领域，既有同步伺服电机，也有异步伺服电机。既有小力矩高转速电机，也有大力矩低转速电机。既有平滑响应特性电机，也有同步响应电机。以德国AMK公司伺服电机为例，同步伺服电机的转子时间常数通常为0.01s，异步伺服电机的转子时间常数通常大于0.01s。以德国AMK公司KE/KW伺服模块为例，电机驱动输出频率范围为0～800Hz，模块内PWM控制频率达8kHz。模块内部增量控制算法模型的同步时段固定为0.5ms。在同步位移应用中，应用组态的SERCOS同步时段ID2等于设定源同步采样时段ID32958等于0.5ms的整数倍。可见，从控制算法模型内部同步时段，到应用同步时段，再到驱动输出频率，最后到电机转子响应过程说明：对同步时段和主轴设定源加速度等是有应用边界限制条件的，否则应用失控或控制波动太大。

根据在昆明卷烟厂对德国HAUNI公司高速卷烟机PROTOS2伺服系统技改实践经验确定的应用边界为：1）A≤1/4；2）最小应用同步时段t1=1ms，n=2，t=2ms；3）a+A＜轴设定的最大加速度为ID113/ID32780。

3 补偿方法

设定源滞后补偿与闭环控制中设定与反馈间的滞后补偿的概念不同，但设定源滞后补偿是以闭环控制滞后补偿为前提的。只有进行了闭环控制滞后补偿，才能假设轴的实际位移等于同步设定位移，本文研究基于这种假设。

设当前速度从0平滑连续平缓提速到Vm，经历m个2ms同步时段或2m个1ms同步时段。2ms同步时段的轴共进行m次设定源同步采样滞后补偿。鉴于同步齿轮传动的齿数为整数，齿数越多，精度越高，不存在误差累计问题。同理2ms设定源同步位置采样值为整数，计算的同步增量值为同步速度也是整数，计算的同步速度增量值为加速度∈{0,1}也是整数。因A=1/4，2ms同步采样计算的同步加速度样本中有m/2个1和m/2个0。

A=1/4，n=2带入式(3)计算出每个2ms同步时段补偿加速度a=1/8，实际加速度补偿样本中有m/8个1和7×m/8个0。即m次补偿中，有m/8次加速度补偿1，每次补偿作用时间2ms，共补偿位移m/4主轴编码器位移。与式(2)计算m×△St=m×2×1×1/4/2=m/4的结果一致。

考虑到补偿后的加速度应小于最大允许加速度限制，编程时选择采样同步加速度为0的时段进行补偿。

表1 设定源同步采样与同步位移统计规律

【】【】

4 实际应用

在实际应用中，已知同步时段倍长系数n和第m个t同步时段采样的速度Vm。显然，经历m个t同步时段，硬件虚拟主轴速度从0变化到Vm。据式(1)又可得到t=n×t1同步时段从轴相对于t1同步时段从轴对应Vm采样速度的位移补偿量Sm，算式如下：

对于任一时刻T=m×t，采样得到速度Vm，就可以算出Sm，从而确定了位移补偿的目标。编程实现过程中设计变量S，当Vm=0时，Sm=0，S=0；当Vm≠0时，如S≠Sm，则调用补偿方法；一旦S=Sm，补偿完成。启动补偿方法后，对应每个t同步时段，采样速度补偿Vi±1，实质是采样加速度A±1。根据牛顿运动定律，同步补偿位移△S=t2/2，S=∑△S。因同步过程控制工艺对△S是有限幅的，且伺服控制从轴对加速度也是有限幅的，故应平估补偿方法的可行性，既应用边界限制。本补偿控制属前馈开环控制，这种补偿控制作用在伺服同步控制的设定源环节，不影响伺服轴的内部控制环节。

5 补偿角度

以上给出了从轴因同步时段差异导致的设定源同步采样位移差对设定源同步采样值进行的补偿的原理和方法。适用于位置同步和角度对齐同步。对于角度对齐同步，把式(1)计算的设定源同步采样位移累计差补偿到同步角度上也是可行的。每当式(1)计算的位移累计差达到率定的门槛值，则把位移累计差转换成从轴的角度偏差直接加到设计的同步角度上，对同步角度进行补偿。对同步角度补偿的应用条件是：设计同步角度加补偿角度的值应小于该轴编码器模值的正数，即大于0，小于|P_2π|值。

6 结束语

本文通过简化建模分析给出了同步时段差异导致设定源同步采样位移差对设定源同步采样值进行的补偿的原理和方法。结合工程实践经验给出了方法的应用条件。尽管以硬件虚拟主轴及结构的多轴同步控制系统为研究对象，但对于软件虚拟主轴及结构的多轴同步控制系统，分析出的原理和方法也有参考价值。文中以加速过程为例展开分析研究，减速过程的道理相同。加速阶段，正补偿；减速阶段，负补偿；速度不变，加速度为0，补偿值也不变。由于水平有限，文中错误之处在所难免，希望专家同行批评指正。

参考文献：

[1]蔡杏山.步进与伺服控制技术[M].北京:人民邮电出版社,2012,1.

[2]王德吉.AMK伺服控制系统原理及应用[M].北京:机械工业出版社,2012,9.

[3]陈先锋.伺服控制技术自学手册[M]北京:人民邮电出版社, 2010.

[4]AMK.AMKASYN AMK Commissioning and Parameter Setting Explorer AIPEX[M].2007.

[5]AMK.AMKASYN Programming (IEC61131-3) AMK Library[M].2007,4.