基础实 思维活 能力强——“智慧乘法运算”教学小实验的实践与反思

钱敏超

《数学课程标准（2011版）》中将“运算能力”作为十个核心概念之一，并指出“运算能力是指能够根据法则和运算律正确地进行运算的能力。培养运算能力有助于学生理解运算的算理，寻求合理简洁的运算途径解决问题。”乘法教学在小学阶段“数与代数”的学习中有着举足轻重的作用。如何通过乘法知识的教学培养学生的运算能力？我们选用浙江省新思维教育科学院张天孝老师编写的“智慧乘法运算——数学超市”材料，对课堂学习内容进行补充与拓展，旨在激发学生学习潜力，发展高层次思维能力。

一、实验基本情况

1.人员组成。

学生自主报名，按学习能力强、中、弱各选4人，共计12人；其中男生、女生各6人；指导教师1人。

2.教学材料。

“智慧乘法运算——数学超市”材料（以下简称“智慧超市”），包含多位数乘一位数、两位数乘两位数这两部分内容。该材料注重学生获得运算结果的思考过程，通过展开运算过程培养学生的运算能力、推理能力，提高思维的批判性和创造性。

3.实验步骤。

实验分两个阶段进行，2016年11月14日到12月9日为第一阶段；2017年4月14日到5月5日为第二阶段。两个阶段中，每周一到周五安排每天20分钟的学生独立作业时间；每周六上午9:00~11:00，安排教师和学生围绕典型材料进行教学互动；合计实验时间约30小时。

第一阶段，主要配合人教版教材三年级上册“多位数乘一位数”这一单元的教学进度，进行适度拓展。拓展内容可简单分为两类。一类为强化算理，主要有：（1）增加乘法分配律和结合律的学习；（2）基于分配律的拆分训练，强调位值，如 46×2＝80＋□、71×5＝□＋5；逆向题：320＋24＝□×□、320＋72＝□×□；（3） 开展三位数乘一位数算法多样化的探索，强化思维的合理性和灵活性；（4）引进组块计算，如已知37×3＝111，求 37×6，74×3等。另一类针对技能，主要有：（1）专项训练多位数乘法中可能发生的乘法运算，如6×8＋2，8×6＋4；几百几十加两位数，如 480+64，280+63；（2）进行两位数乘一位数六种类型的口算强化训练，并组织了过关测试。（两位数乘一位数可以分为六种类型：①十位积、个位积都不进位，如11×3；②十位积进位，个位积不进位，如61×3；③十位积不进位，个位积进位，如16×3；④十位积、个位积都进位，乘积十位叠加不进位，如66×3；⑤十位积不进位，个位积进位，乘积十位叠加进位，如36×3；⑥十位积、个位积都进位，乘积十位叠加进位，如 69×3。）

第二阶段，重点开展两位数乘两位数的“口、笔算结合”实验，教学序列如下：（1）算法多样化的展开与通法概括；（2）探索两位数乘两位数的新算法（含新的竖式计算方法）：①几十一乘几十一，如41×31；②十几乘十几及相关类型，如 14×16、23×24、34×36；九十几乘九十几及相关类型，如97×96、87×85、76×76；五十几乘五十几及相关类型，如52×56、67×63、46×42；③一方相同，另一方和为 10，如 45×65、39×31；④组块计算。

（例“五十几乘五十几”计算方法，其余计算方法见张天孝老师编写的《智慧乘法实验材料》）

4.学习形式。

周一到周五，学生使用“智慧超市”材料自主作业，该过程教师不参与指导。每周六上午对作业中具有典型意义的疑难问题进行交流、分析、讲解和巩固练习。

二、实验结果与分析

1.两位数乘一位数口算掌握情况。

如前述，两位数乘一位数可以分为六种类型。根据这六种类型，在实验过程中进行了三次学习检测。第一次检测含第①②③三种类型；第二次检测含第④种类型；第三次检测含第⑤⑥两种类型。每次检测用时5分钟，题量为45题，直接使用“智慧超市”材料中的检测题。统计结果如下：（单位：题/人，下同）

实验组　43.83　42.00　41.33对照组　40.27　36.67　32.81平均做对题数第①②③类　　第④类　　第⑤⑥类

分析：实验组的总体情况领先于对照组；其中第①②③类两组学生差别不是很大，均达40题以上；第⑤⑥两类的差别较明显，分析原因主要是第⑤⑥两类题目中含有“乘积十位叠加进位”，如计算 69×8时，乘积十位“6×8＋7”需要进位，实验组学生经过专项训练获得了较为明显的优势。

2.两位数乘两位数计算掌握情况。

“两位数乘两位数”进行了一次评价检测。检测用时5分钟，题量为30题，随机排列。含：①几十一乘几十一类型（4题）；②十几乘十几及相关类型（4题）；③九十几乘九十几及相关类型（4题）；④五十几乘五十几及相关类型（6题）；⑤一方相同，另一方和为10（4题）；⑥组块计算类型（2题）；⑦其他类型（6题）。具体题目如下：

41×31＝　94×98＝　58×29＝　52×54＝　98×15＝27×23＝　71×21＝　93×96＝　35×12＝　57×59＝12×13＝　54×54＝　81×91＝　95×86＝　14×15＝23×25＝　25×36＝　89×81＝　11×35＝　83×97＝62×54＝　75×18＝　18×91＝　73×77＝　31×33＝37×27＝　45×47＝　53×56＝　41×26＝　42×47＝

统计结果如下：

实验组　　对照组平均做对题数　25.75　14.75平均正确率　85.83%　59.00%

从上表我们发现：实验组学生的运算结果遥遥领先。我们又进一步对学生在计算过程中所表现出来的计算策略进行了分析和比较，结果如下：

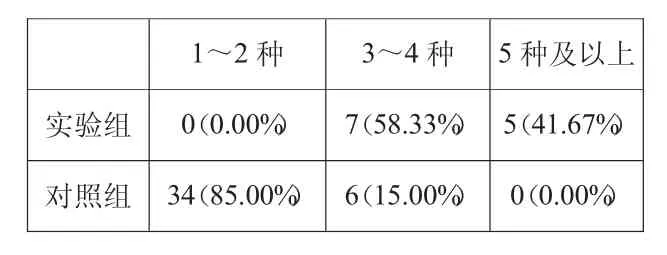
1～2种验组　0（0.00%）　7 3～4种　5种及以上实（58.33%）　5（41.67%）对照组　34（85.00%）　6（15.00%）　0（0.00%）

如《数学课程标准（2011版）》所言，运算能力主要体现在学生能根据算式特点，选择合理、简捷的运算途径进行计算。分析上表我们可以发现：对照组学生的计算策略比较单一，85%的学生只呈现出1～2种计算策略；而实验组学生在计算过程中能够分析算式的特点，有合理选择方法的意识和能力，普遍呈现出多种计算策略。

如实验组一位学生的作品，她对算法的选择和使用达到了熟能生巧的水平。在短短五分钟里，她根据数据特点，分门别类，针对性地使用了七种运算策略。

由此可以看出，“智慧超市”材料内容的编排，揭示了数学的内在联系、符合学生的认知规律、有效提升了学生的运算能力。

三、进一步的学习成效

1.多样、开放的学习材料，开阔了学生的眼界。

“智慧超市”系列材料强调发挥学生的主体性，不强求学生一定要按“标准程序”计算，而是鼓励学生独立思考，自主创造个性化的计算方法。学生经常参与自主探索和相互交流算法的实践，就会逐步树立起开放、自主的学习信念。

如计算“36×15”，参与实验的学生一共提出八种不同的计算方法——思维的开放性和灵活性可见一斑。

（1）36×15＝（30＋6）×15＝450＋90＝540

（2）36×15＝（10＋5）×36＝360＋180＝540

（3）36×15＝（40－4）×15＝600－60＝540

（4）36×15＝（20－5）×36＝720－180＝540

（5）36×15＝36×5×3＝180×3＝540

（6）36×15＝9×4×15＝9×60＝540

（7）36×15＝6×6×15＝6×90＝540

（8）36×15＝9×4×5×3＝27×20＝540

更重要的是，这种开放和灵活的思维习惯能更广泛地迁移到学习和练习中。

2.重视分析数与数之间的关系，发展学生的推理意识和推理能力。

如前所述，“智慧超市”材料中设计了几百几十加两位数的系列计算练习，如“540＋45＝□□×□”这样的问题。思考过程是：首先，回忆积为54和45的乘法口诀，确定它们都有哪个乘数（公因数）——6×9＝54、5×9＝45，确定其中一个乘数是9，另一个乘数十位是6，个位是5，即65。经过这样的训练，一位同学在做三位数乘一位数之“踢十法”专项训练时（如 346×7＝306×7＋40×7，学生把这种先不算十位的方法称为“踢十法”），把本来仅仅局限于加法技能的练习，当作了推理训练的材料。例：832+560=□□□×□，通过分解832和56的因数，推导出与这道加法相联系的乘法“174×8”。这样的思考，无疑是非常独特的。

又比如，我们发现实验组有位学生对一道计算练习做了如下小笔记——

通过访谈，我们得知该生的解答过程别具一格。他先确定各算式乘积的个位分别是几，按个位情况把算式和得数进行分类；再通过乘数的十位相乘来估算、锁定正确结果。以“34×29、28×32和18×32”为例，乘积的个位都是“6”，分别对应的必然是 576、986、896；通过十位相乘来估计，34×29、28×32 的结果必然大于600，所以 18×32 应连 576；继续观察 34×29和28×32这两个算式，发现 34＞32，29＞28，推知 34×29＞28×32，那么 34×29 连 986，28×32 连 896。

“智慧超市”不囿于算出正确的结果，而是把学习重心转向获得结果的思考过程。计算任务的设计精巧、独特，序列合理，能有效提升学生的运算能力和发展推理能力，为数感和创新思维的发展留下了广阔的空间。