带有Rellich项的临界双调和方程组的研究

康东升,刘晓楠，曹玉平

(1 中南民族大学 数学与统计学学院,武汉 430074； 2 中南民族大学 图书馆,武汉 430074)

1　相关知识

首先在全空间中研究下面带有Rellich项的临界双调和方程组：

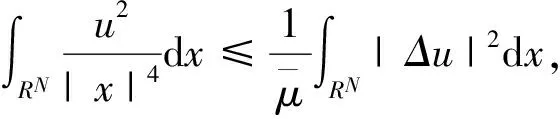
(2)

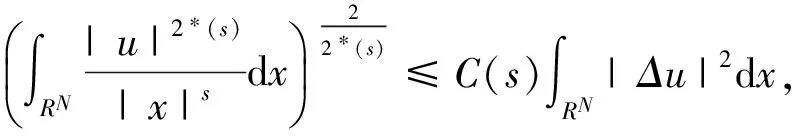
(3)

由(2)和(3)式我们定义下面的Rellich-Sobolev常数[1]：

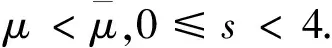
假设(H1)成立,由文[1]可知S(μ)的达到函数是:

(4)

其中Uμ(x)>0是径向对称、单调递减的,并且满足下面条件[1,2]：

从文[1]可知Uμ(x)是下列方程组的解：

下面在D2,2(RN){0}中定义最佳常数[1,3]：

Sη,α,β(μ):=

(5)

我们设:

(6)

这里τmin≥0是f(τ)的最小值点.

本文中的基态解是指在所有解中对应能量值最小的解，因此(5)式被达到时的解是基态解.

其次,我们证明下列方程组解的存在性：

(7)

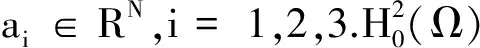
方程组(7)对应的能量泛函为：

J(u,v):=

(8)

其中u,v∈H,J∈C1(H×H,R).对于(u,v)∈H×H(0,0),如果J′(u,v),(φ,φ)=0，∀(φ,φ)∈H×H,那么我们称(u,v)是方程组(7)式的解.接下来,我们假设：

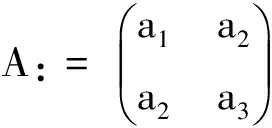
下面定义本文中一些常用的符号：

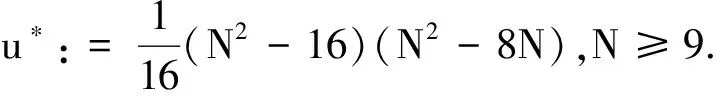
本文的结论如下：

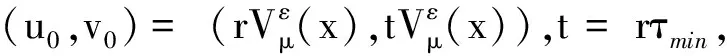
定理2假设N>8,0≤μ≤μ*,并且(H1)和(H2)成立，则方程组(7)至少存在一个解(u,v)∈(H{0})2.

为了书写方便,全文用C表示常数；用O(εt)表示|O(εt)|/εt≤C；用o(εt)表示|o(εt)|/εt→0；用O1(εt)表示C1εt≤|O1(εt)|≤C2εt(当ε足够小时),并且省略dx.

2　定理1的证明

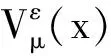
证明与文献[3]中定理1.1及文献[5]中定理5类似,在此省略.

由f′(τmin)=0可以推出τmin是下列方程的一个根：

g(τ):=2*(s)+ηατβ-ηβτβ-2-2*(s)τ2*(s)-2=0,

τ>0.

(9)

假设ε>0,u∈D2,2(RN),r>0，若方程组(1)有正解并且解的形式为(ru,tu),则可得到：

(2*(s)+ηατβ)r2*(s)-2=2*(s)=(2*(s)τ2*(s)-2+

(10)

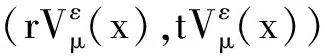
证明与文献[6]中引理2.2类似,在此省略.

定理1的证明我们应用与文献[6]中定理1.1类似的方法来证明本定理.设(u0,v0)是方程组(1)的基态解，首先我们证明：

(11)

同样地,记：

(12)

容易得到：

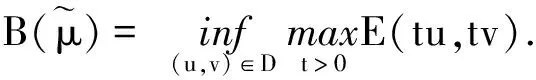
(13)

令

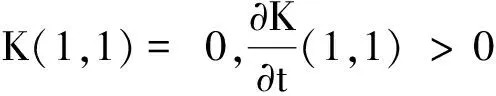
因此(11)式成立.

同理可得：

(14)

因此由(11)、(14)式得：

(15)

由(10)式得到：

(16)

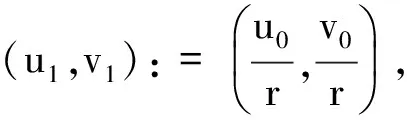
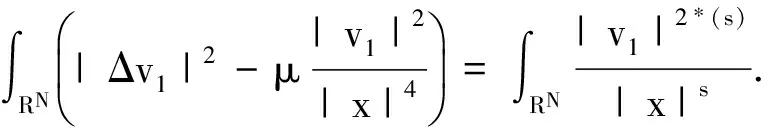
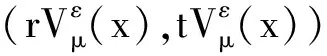
由此

(17)

所以u1,v1是下面方程的基态解：

由Hölder不等式、(11)式及(14)式得到：

3　定理2的相关引理

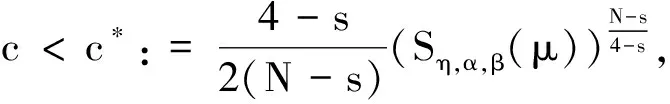
证明与文献[3]中引理2.4.1类似,在此省略.

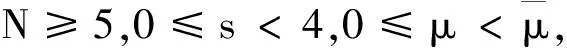
当N≥8,

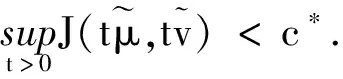
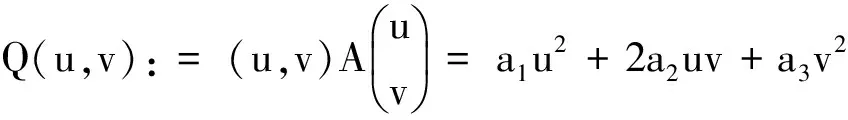
g1(t):=J(tuε,tτminuε)≤

另一方面有：

注意到：

0≤μ2,μ=μ*⟺b(μ)-δ=2,2*(s)>2.

(18)

由(18)式、引理1和引理4得出：

由上式及引理4得到：

引理5证毕.

定理2的证明过程与文献[3]中定理1.2类似，在此省略.

[1]Kang D, Xu L. Asymptotic behavior and existence results for the biharmonic problems involving Rellich potentials[J]. Journal of Mathematical Analysis and Applications, 2017, 455:1365-1382.

[2]Jannelli E, D′Ambrosio L. Nonlinear critical problems for the biharmonic operator with hardy potential[J]. Calculus of Variations in Partial Differential Equations, 2015, 54:365-396.

[3]Huang Y, Kang D. On the singular elliptic systems involving multiple critical Sobolev exponents[J]. Nonlinear Analysis Theory Methods and Applications, 2011, 74(2):400-412.

[4]熊萍.带有多重Rellich 项的临界双调和方程组[D].武汉：中南民族大学,2017: 6-7.

[5]Alves C, Filho D, Souto M. On systems of elliptic equations involving subcritical or critical Sobolev exponents[J]. Nonlinear Analysis Theory Methods and Applications, 2000, 42(5):771-787.

[6]Peng S, Peng Y, Wang Z. On elliptic systems with Sobolev critical growth[J]. Calculus of Variations in Partial Differential Equations,2016, 55:142.

[7]Chen Z, Zou W. Positive least energy solutions and phase separation for coupled Schrödinger equations with critical exponent: higher dimensional case[J]. Calculus of Variations in Partial Differential Equations,2015,52:459-460.