基于自适应差分进化算法的高维模糊度搜索
孙妍艳,刘翠芝
(东北大学 资源与土木工程学院测绘工程系,辽宁 沈阳 110819)
0 引 言
整周模糊度解算是实现快速、高精度定位的关键,一直是全球导航卫星系统(GNSS)的研究热点。在GNSS定位中,定位所需的时间取决于正确确定整周模糊度所需要的时间。目前,国际上应用最为广泛的是LAMBDA(Least-square Ambiguity Decorrelation Adjustment)算法。对高维模糊度解算算法的研究早期主要是基于LAMBDA算法加快去相关的速度。如Li and Gao提出的高维解算算法只对7~13维数据有效[1]。Teunissen等[2]提出的MCLAMBDA方法,使得LAMBDA算法适用于多基线姿态测量。后来,从格理论的角度证明了整数最小二乘模糊度解算相当于格上最近向量问题后,许多学者提出了LLL规约算法在模糊度解算中的应用[3-7],但LLL算法存在规约耗时较长且明显大于搜索耗时的问题。
近些年,有学者提出利用遗传算法固定整周模糊度[8-9],但都只是对某一维度的模糊度进行解算分析,并没有对更高维的模糊度进行分析,也没有对这种群智能算法在模糊度解算应用中的各项参数设定进行深入的研究。本文利用比遗传算法更智能的差分进化算法对高维模糊度进行固定。
差分进化算法(DE)是由美国学者Store和Price在1995年提出的一种智能计算方法,初衷是用于求解切比雪夫多项式的问题。与其他进化算法大致相同,差分进化算法对函数的可导性甚至连续性都没有要求,适用性很强。Jakob Vester strom和Rene Thomsen将差分进化算法、遗传算法、粒子群优化算法进行对比实验分析,指出差分进化算法在解决复杂优化问题方面的收敛速度更快、稳定性更强[10]。
但高维问题属于复杂的优化问题,标准差分进化算法无法满足问题的求解要求。且算法在运算后期,很容易陷入局部最优解也就是“早熟”的现象或者收敛缓慢致使在有限的迭代次数中无法收敛到最优解的情况。因此本文采用自适应差分进化算法进行高维模糊度解算,并设计了一个更具有普遍适用性的算法。
1 数学模型及原理
1.1 整数最小二乘原理
GNSS整周模糊度的解算一般包括两部分:模糊度估计和模糊度确认。其中,模糊度估计分为两步:首先,通过最小二乘方法或卡尔曼滤波法求出模糊度的浮点解N及其方差协方差阵QN; 然后,按照一定的规则确定模糊度整数解的搜索空间,在此空间中按照模糊度残差二次型最小的原则利用某种搜索算法固定模糊度。模糊度的残差二次型为[11]
联系人: 孙妍艳E-mail: 767564911@qq.com
min(N-N′)TQN-1(N-N′),
(1)
式中,N′∈Zn,是模糊度的固定解。
1.2 差分进化算法原理
差分进化算法是一种基于种群的全局搜索算法,通过把一定比例的多个个体的差分信息作为个体的扰动量,使得算法在跳跃距离和搜索方向上具有自适应性。如图1所示,在进化的早期,因为种群中个体的差异性较大使得扰动量较大,从而使得算法能够在较大范围内搜索,具有较强的勘探能力;而到了进化后期,当算法趋于收敛时,种群中个体的差异性较小,算法在个体附近搜索,这使得算法具有较强的局部开采能力[12]。
标准差分进化算法的原理是:首先,随机生成初始种群,从种群中随机选择两个个体向量的差分量作为第三个随机基准向量的扰动量,得到变异向量,然后变异向量与基准向量进行杂交,生成试验向量,最后,采用贪婪选择机制,将基准向量与试验向量竞争,适应度高者保存到下一代种群中。从而,种群逐渐聚集到最优解的位置。
目前,差分进化算法已广泛应用于很多领域,如人工神经网络,化工,电力,机械设计,机器人,信号处理,生物,运筹学,控制工程,数据挖掘,调度问题等并取得了惊人的效果[13]。其缺点是,差分进化算法并没有一个系统的研究,所以每个领域都要根据其自身的特点进行算法设计。
2 自适应差分进化算法设计
本文参考Brest[14]等提出的自适应差分进化算法(jDE),使缩放因子F和杂交概率Cr与种群个体一同编码和进化。 与jDE算法不同是,本文将jDE算法中的F取值条件由rand[0,1]<0.1改为rand[0,1]<0.5,其中rand[0,1]为0~1之间均匀分布的随机数。目的是为了使样本能够生成更多的变异个体,以保证样本具有足够的多样性,从而加快算法的收敛速度。
2.1 适应度函数
适应度函数是选择操作中判优的参考条件。在模糊度解算中,适应度函数越小越好,即J(N)越小,表明该N′越接近最优解。
(2)
2.2 初始化操作
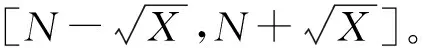
2.3 变异操作
变异操作是指种群个体中某个元素发生改变。设t为当前运行次数,V为变异向量,u为试验向量即基准向量和变异向量交叉生成,Ni为第i个基准向量,Ni1、Ni2、Ni3为从当前种群中随机选择三个向量,其中i1、i2和i3是从集合{1,…,NP}中随机选择的相互不同的整数且不等于i.
F的自适应调整策略的数学表达式:
OldFi(t)=Fi(t).
NewFi(t)=
(3)
变异操作的数学表达式为
Vi(t)=Ni1(t)+NewFi(t)(Ni2(t)-
Ni3(t)) .
(4)
尽管目前提出了许多变异操作的方法,但是通过实验分析,采用公式(4)更适合模糊度的解算。
2.4 修补操作
修补操作是为了检查变异后的模糊度分量是否超出其取值范围。如果超过,对其进行修正。
2.5 杂交操作
杂交操作可以提高种群的多样性,差分进化算法的杂交操作与其他进化算法的不同之处在于其采用的是父代的基准向量和变异向量进行操作,而其他进化算法是基于多个来自父代的基准向量交换基因的杂交操作。本算法采用二项式杂交算子。杂交后得到试验向量u.试验向量与基准向量和变异向量都不相同。杂交操作是对个体中的每一个元素进行操作。
Cr的自适应调整策略的数学表达式:
OldCri(t)=Cri(t),
NewCri(t)=
Cri(t+1)=
(5)
杂交操作的数学表达式:
ui,j(t)=
(6)
2.6 选择操作
采用贪婪的选择机制,如果试验向量的适应度值好于基准向量,则保留试验向量到下一代种群中,否则保留基准向量。
2.7 终止迭代次数
终止迭代次数不宜过小或过大,过小时搜索不到全局最优解,过大时增加搜索时间,降低搜索效率。终止迭代次数建议值为100~200.
3 实验结果与分析
3.1 实验方案
差分进化算法无论是参数的设定还是每一代种群的产生都具有一定的随机性,但这种随机性并不是盲目的随机,而是基于上一代种群的随机。所以,最终一定可以得到最优解。如果算法连续独立运行一定的次数,且每一次都能得到全局最优解,则说明该算法具有一定的稳定性。所以本实验的每组数据都连续做50次的伯努利实验;将结果与LAMBDA算法的结果进行对比,若两种算法结果相同,则表明该自适应差分进化算法得到的是正确解,从而可以验证算法的正确性。本文分别基于实测和模拟数据进行统计分析本算法的正确性、稳定性及平均运算速率。
本算法的参数设置如下:缩放因子F的初值设为0.5,杂交概率Cr的初值为0.9,终止迭代次数为50.
3.2 实验1
采用的是文献[17]中3维整周模糊度的解算实例,目的是为了验证本文算法的可行性。图2示出了一共进行50次实验,每次实验搜索到最优解时的迭代次数以及最优解所对应的模糊度残差二次型数值。从图2可以看出50次实验中搜索到最优解的最大迭代次数为8,且每次实验模糊度残差二次型都收敛于同一个值,说明算法具有较好的稳定性。并与LAMBDA算法进行了结果对比,二者结果一致。解算结果如表1所示。
N=[5.4500,3.1000,2.9700];

表1 3维模糊度的固定解及其二次型数值
3.3 实验2
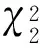
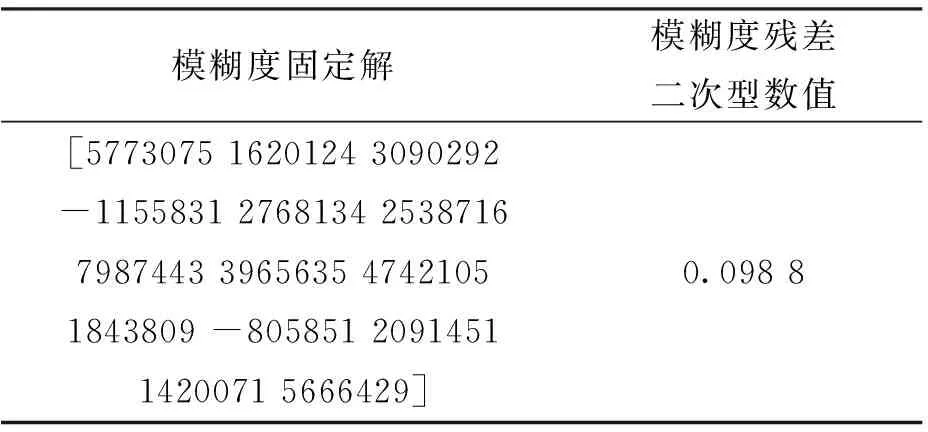
表2 14维模糊度的固定解及其二次型数值
3.4 实验3
为了分析算法的普遍适用性程度,分别模拟生成15、20以及40、50、60维数据。采用文献[18]的模拟方法进行实验数据模拟。模糊度的浮点解构造为
N=100×randn(n,1) ,
(7)
其中,n为模糊度的维数,randn(n,1)为随机生成的n个服从标准正态分布的数值。
由于方差协方差阵为实对称矩阵,所以按照公式(8)生成QN:
QN=LTDL,
(8)
式中:L为随机生成的n维正交矩阵;D为随机生成的n维对角矩阵。
图4(b)表明平均速度比图4(c)快,是因为图4(c)所示的模糊度浮点解的精度没有图4(b)所示好,所以,图4(c)表明收敛到最优解的速度比图4(b)慢些。解算结果如表3所示。

表3 15维模糊度的固定解及其二次型数值
20维和40维的数据找到最优解的平均迭代次数大约在13和36次,如图5和图6所示。20维数据的寻优速度明显比15维图4(b)、图4(c)要快,是因为其模糊度浮点解的精度比较好。解算结果如表4、表5所示。

表4 20维模糊度的固定解及其二次型数值
表6示出了本文算法与LAMBDA算法在运行效率上的对比,说明该算法在运行效率上略优于LAMBDA算法。
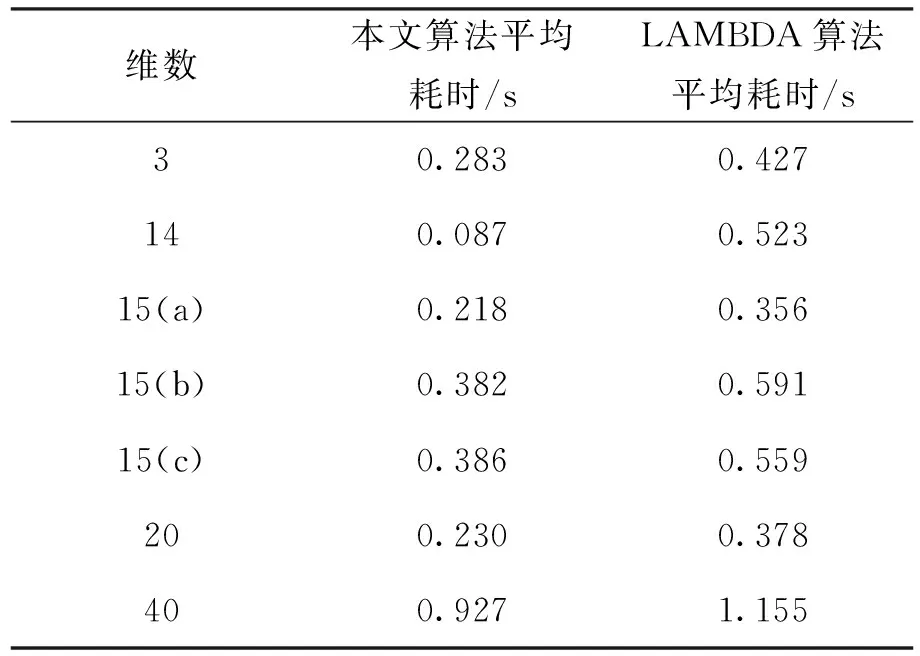
表6 本文算法与LAMBDA算法运算效率比较
最后,笔者试算了50维和60维的模糊度,对于模糊度精度比较高的数据可以在运算50次之内找到最优解,但是算法的稳定性不是很好。即使增加迭代的步数,稳定性也没有明显的改善。
4 结束语
本文将智能算法中的DE算法应用于整周模糊度的搜索中,并根据整周模糊度解算过程中数据的特点,将Brest等提出的自适应差分进化算法进行改进,使其更适用于模糊度最优解的搜索。通过实测和模拟多组高维数据,对本算法进行了效果验证与分析。可以得出以下结论:
1) 该自适应算法可以用于整周模糊度的固定。对于40维以下的整周模糊度,该算法可以达到99.9%的固定,算法具有较好的稳定性和通用性。但对于更高维的模糊度,解算效果不是很好,需要进一步改善算法,以加快算法的收敛速度。
2) 通过比较本文算法和LAMBDA算法的平均运算效率,发现本文算法基本上略快于LAMBDA算法。说明本算法可以用于模糊度的快速搜索。
3) 对于算法在迭代的后期容易出现“早熟”问题,通过设置较大的迭代次数,并不能从根本上解决此问题。应该深入研究变异算子和杂交算子,才能加快收敛速度。
[1]LI Z, GAO Y. A method for the construction of high-dimensional transformation matrices in Lambda [J].Geomatica,1998(52):433-439.
[2]TEUNISSEN P J G. A General multivariate formulation of the multi-antenna GNSS attitude determination problem [J]. Artificial Satellites, 2008, 42(2): 97-111.
[3]卢立果, 刘万科, 李江卫. 降相关对模糊度解算中搜索效率的影响分析 [J]. 测绘学报, 2015, 44(5): 481-487.
[4]BORNO M A, CHANG X W, XIE X H. On ‘decorrelation’ in solving integer least-squares problems for ambiguity determination [J]. Survey Review, 2013, 46(334): 37-49.
[5]CHANG X W, YANG X, ZHOU T. MLAMBDA: a modified LAMBDA method for integer least-squares estimation [J]. Journal of Geodesy, 2005, 79(9): 552-65.
[6]刘万科,卢立果,单弘煜. 一种快速解算高维模糊度的LLL分块处理算法 [J]. 测绘学报, 2016(2): 147-156.
[7]卢立果,刘万科,李江卫. 一种有效的LLL规约算法 [J]. 武汉大学学报(信息科学版), 2016(8): 1118-1124.
[8]刘智敏,刘经南,姜卫平, 等. 遗传算法解算GPS短基线整周模糊度的编码方法研究 [J]. 武汉大学学报(信息科学版), 2006(7): 607-609,631.
[9]阳仁贵,欧吉坤,王振杰, 等. 用遗传算法搜索GPS单频单历元整周模糊度 [J]. 武汉大学学报(信息科学版), 2005(3): 251-254,259.
[10]VESTERSTROM J, THOMSEN R. A comparative study of differential evolution, particle swarm optimization, and evolutionary algorithms on numerical benchmark problems[C]// Evolutionary Computation, 2004. CEC2004. Congress on. IEEE, 2004(2):1980-1987.
[11]TEUNISSEN P J G. The least-squares ambiguity decorrelation adjustment: a method for fast GPS integer ambiguity estimation [J]. Journal of Geodesy, 1995, 70(1-2): 65-82.
[12]武志峰. 差异演化算法及其应用研究 [D]. 北京交通大学, 2009.
[13]汪慎文,丁立新,张文生, 等. 差分进化算法研究进展 [J]. 武汉大学学报(理学版), 2014(4): 283-92.
[14]BREST J, GREINER S, BOSKOVIC B,etal. Self-Adapting Control Parameters in Differential Evolution: A Comparative Study on Numerical Benchmark Problems [J]. IEEE Transactions on Evolutionary Computation, 2006, 10(6): 646-57.
[15]JONGE P D, TIBERIUS C. Integer Ambiguity Estimation with the Lambda Method [M]. Springer Berlin Heidelberg, 1996.
[16]TEUNISSEN P J G, JONGE P J D, TIBERIUS C C J M. The least-squares ambiguity decorrelation adjustment: its performance on short GPS baselines and short observation spans [J]. Journal of Geodesy, 1997, 71(10): 589-602.
[17]DE JONGE P J, TIBERIVS C C J M. The LAMBDA method for integer ambiguity estimation: Implementation aspects [R]. Dekft Geodetic Computing Centre, Delft University of Technology, 1996.
[18]XU P. Random simulation and GPS decorrelation [J]. Journal of Geodesy, 2001, 75(7-8): 408-23.

