计及可靠性评估的中压配电网规划方案比选

杨文丽

(重庆理工大学电气与电子工程学院，重庆 400050)

0　引言

DL/T 1503—2016 中压配电网可靠性评估导则[1]是电力行业首部可靠性评估导则，实现由“事后评价”到“事前事中预测评估”的转变。已有文献结合最新导则对其在中压配电网规划、改造、运行环节的应用进行了研究[2-8]。

当前对于投资方案评估或比选方法，主要是全寿周期成本[9-14]和成本效益[15-16]模型。在不考虑电价浮动的场景下，全寿命周期成本最小化即为效益最大化，此模型在单项或小规模工程项目、输电网项目比选时有较强的实用性。而在新电改背景下，政府将按照“准许成本+合理收益”模式核定电网企业或增量配电网的220 kV及以下的输配电价，且具备条件时实行与供电可靠率、线损率等关键指标挂钩的浮动调价机制[17]。如此，最靠近用户且往往有着较大建设与改造规模的中压配电网，其投资决策者将更加注重成本效益原则，在政府管制框架内通过适度投资，提升供电质量，以尽可能地获取更多的合理利润。

现有计及可靠性评估的成本效益方法研究中，采用“前后对比法”计算可靠性提升效益与改造投资的差值或比值[3]或通过前后供电量之差作为增供电量[18]计算方案成本效益，多适用于电量趋稳、网架成熟的中压配电网或纯增量配电网。而对于部分新建与现存存在关联影响的中压配电网规划而言，因其投资同时用于满足负荷增长、提升供电可靠性和降低网络损耗，采用上述方法计算投资成本效益时涵盖了存量电网容量裕度的贡献纳，无形中扩大了该项投资的效益。而“有无对比法”将“有项目”成本效益逐年与“无项目”作动态比较，求得两者增量成本效益，可衡量投资项目的真实影响、效益和作用[19]。

结合相关理论与工程实践，本文从可靠性参数搜集及计算方法和备选规划方案比选两方面切入，提出了计及可靠性的规划方案形成与比选方法。其中，基于“有无对比法”给出投资项目的增量净效益模型，并分析不同网架供电能力与负荷需求关系下净效益简化模型与常规全寿命周期费用(life cycle cost，LCC)最小化比选方案的异同。基于全寿命周期动态经济指标评估多个投资方案，为决策者提供参考。

1　计及可靠性评估的中压配电网规划方案的形成与比选方法

1.1　基本思路

计及可靠性的中压配电网规划方案的形成与比选方法主要包括现状电网供电可靠性计算、规划方案拟定与可靠性指标计算和基于成本效益模型的方案比选。方案形成与比选的基本思路见图1。

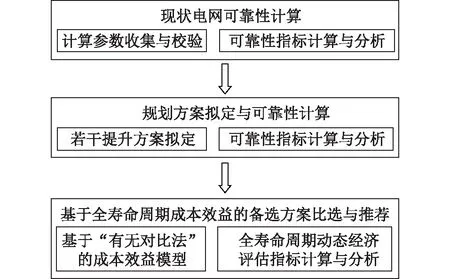
图1　计及可靠性的规划方案形成与比选思路Fig.1　General idea of the formation and selection method of planning schemes considering reliability

1.2　现状电网供电可靠性计算

1.2.1计算参数搜集与校验

搜集及处理基础资料。从相关系统获取供电可靠性计算所需基础资料(如图2所示)，并进行整理、校验处理。

图2　供电可靠性计算所涉参数Fig.2　Power supply reliability calculation parameters

1.2.2可靠性指标计算与分析

基于故障模式后果分析法(failure mode and effect analysis，FMEA)[2]，计算故障停电可靠性指标(预安排类似，略去)。

(1) 枚举单个设备故障，梳理设备故障后开关跳闸、故障隔离、非故障区恢复供电过程，确定该故障对各负荷点的停电影响，进而计算各负荷点的年故障停电次数和年停电持续时间。

① 负荷点年故障停电次数计算公式：

(1)

式中：λL为负荷点L年故障停电次数；δS为设施故障停运率；N为故障后会造成该负荷点停电的设施的集合。

② 负荷点年故障停电小时数计算公式：

(2)

式中：tL为负荷点L年故障停电小时数；tsh设施故障后该负荷点恢复供电时间。

(2) 重复第一步，记录所有设备单独故障后各负荷点的故障停运率和故障停电持续时间，形成故障模式后果分析表。

(3) 计算该负荷点的供电可靠率、缺供电量等可靠性指标。

① 负荷点供电可靠率计算公式：

(3)

式中：KL为负荷点L供电可靠率。

② 负荷点L年缺供电量计算公式：

QENSL=tLPL

(4)

式中：QENSL为负荷点L年缺供电量；PL为负荷点L的负荷。

(4) 依次计算每个负荷点的可靠性指标，并在此基础上计算系统可靠性指标。

① 系统平均停电频率，记作FSAIFI，其计算公式为：

(5)

式中：kL为L负荷点下用户数；M，N分别为系统总负荷点、总用户数。

② 系统平均停电时间，记作tSAIDI，其计算公式为：

(6)

式中：uL为负荷点年停电时间。

③ 系统平均供电可靠率，记作KASAI(%)，其计算公式为：

(7)

④ 系统缺供电量，记作QENS，其计算公式为：

(8)

基于供电可靠性指标，可以辨识薄弱环节，找出对某一可靠性指标影响较大的设备或可靠性参数，便于制定规划方案。

1.3　规划方案拟定与可靠性计算

1.3.1方案拟定

结合区域电量增长需求、可靠性薄弱环节分析和规划预期目标，统筹解决配网结构优化与存量问题，提出满足未来负荷需求、提升供电可靠性的若干规划方案。提升供电可靠性的技术与管理措施如图3所示。

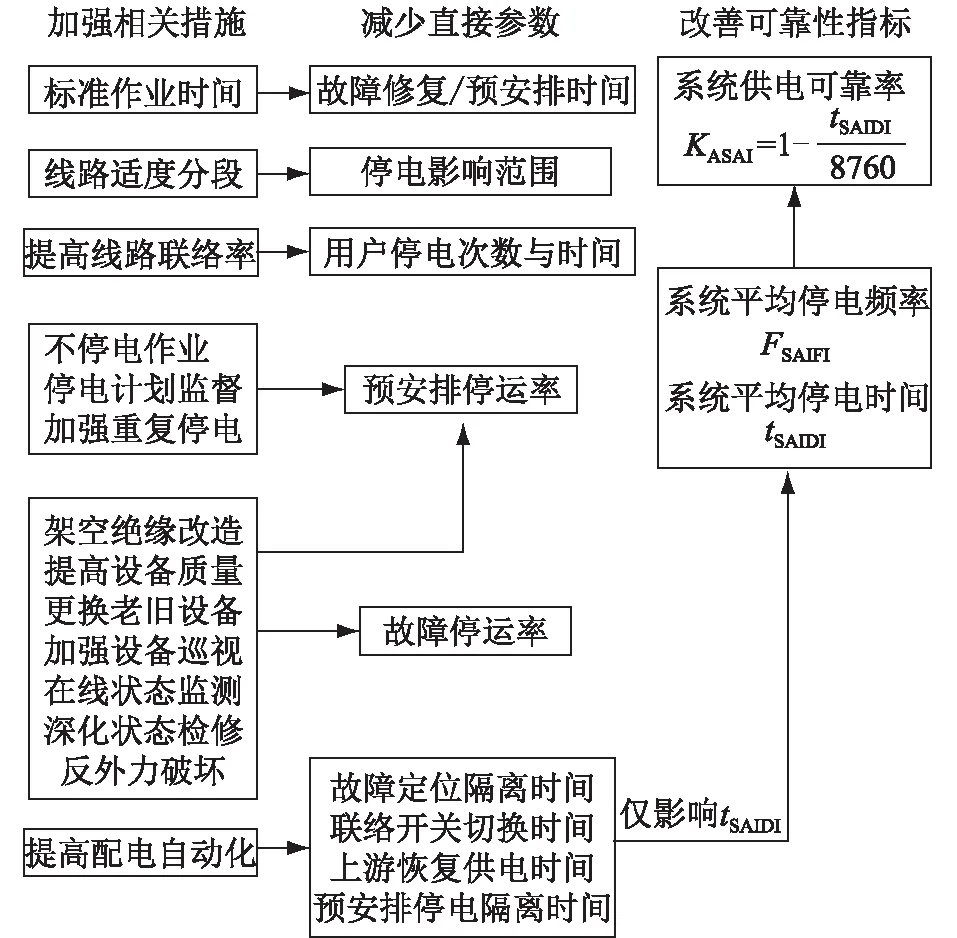
图3　供电可靠性提升措施分析Fig.3　Power supply reliability improvement measures

1.3.2可靠性计算

计算并分析各备选方案的可靠性指标，如平均停电频率、平均停电时间、供电可靠率和期望缺供电量等可靠性指标。

1.4　基于全寿命周期成本效益评估模型的方案比选

1.4.1基于“有无对比法”的成本效益模型

本文设定有/无项目均以“有项目”设备全寿命周期为一个完整的计算期，且不考虑“无项目”的追加投资。第t年中压配电网增量净效益ΔBt计算公式如下：

ΔBt=ΔRt-(Tt′+ΔCyt+ΔClt+ΔCet)

(9)

式中：ΔRt，Tt′，ΔCyt，ΔClt和ΔCet分别为第t年中压配电网的增量电量收入、初始投资、增量运维成本、增量网损成本和增量停电损失。

(1) 增量运维成本。运维成本含材料费、修理费和薪酬等，第t年中压配电网增量运维成本ΔCyt为：

ΔCyt=δytTzt′

(10)

式中：δyt为第t年运维成本率；Tzt′分别为第t年“有项目”中压配电网累计初始投资。其中，“有项目”Tzt′计算公式：

(11)

式中：Tt′ 为第t年“有项目”逐年初始投资；n为计算期，a为建设期。

本文假定运维成本率在计算初期、中期和末期近似呈浴盆状变化。运维成本率δyt近似计算公式：

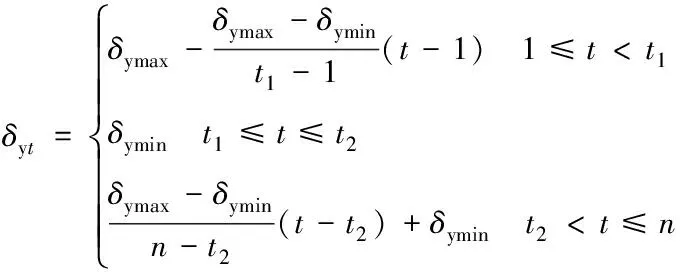
(12)

式中：δymax为计算初、末期运维成本率；δymin为计算中期运维成本率；t1，t2为浴盆曲线平稳期两时间节点。

(2) 增量网损成本。第t年中压配电网增量网损成本ΔClt：

ΔClt=τmax(Plt′J′-PltJ)

(13)

式中：Plt′，Plt为第t年有、无项目时中压配电网最大负荷水平下的网络损耗；τmax为最大负荷年损耗小时数；J′，J为有、无项目上下级平均配电价差额[15]。

(3) 增量停电损失。第t年中压配电网增量停电损失ΔCet为：

ΔCet=η(QENSt′-QENSt)Jet

(14)

式中：η为年负荷率，η=Tmax/8760；QENSt′，QENSt分别为第t年有、无项目时中压配电网最大负荷水平下的缺供电量，由本文前述可靠性评估算法求得；Jet每年单位停电损失。

(4) 增量净效益。为评估某一期规划在整个计算期的收益，采用下式计算各年增量电量收入ΔRt：

ΔRt=Tmaxt(Pt′J′-PtJ)

(15)

其中：

(16)

(17)

式中：Pt′，Pt分别为计算期内各年有、无项目中压配电网计算负荷，与各自满足N-1条件下的供电能力CA，CA0相匹配；Pmaxt为规划区域实际负荷需求。

结合式(9—17)，得到基于“有无对比法”的增量净效益ΔBt：

ΔBt=ΔRt-(Tt′+ΔCyt+ΔClt+ΔCet)=
Tmaxt(Pt′J′-PtJ)-[Tt′+δyTzt′+τmax×
(Plt′J′-PltJ)+η(QENSt′-QENSt)Jet]

(18)

(5) “有项目”增量净效益模型分析。结合网架供电能力和区域负荷需求关系(见图4，抽象对比)，在式(18)基础上分析不同场景下“有项目”的增量净效益计算模型。

曲线CA0为保持现状的“无项目”供电能力曲线；CA-1、CA-2和CA-3为不同场景下“有项目”供电能力曲线；P′-1、P′-2和P′-3分别为相应场景下“有项目”区域负荷需求曲线(与网架供电能力相匹配)。a为建设期结束节点；n为计算期结束节点。

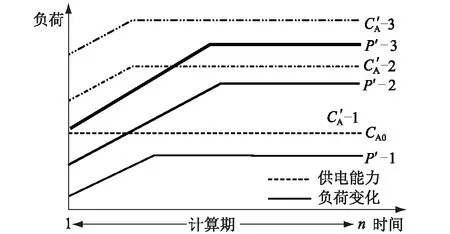
图4　不同场景下的负荷需求与供电能力Fig.4　The load demand and power supply capability in different scenarios

① 场景一：CA0、CA-1和P′-1构成“现状网架较为成熟、供电能力满足未来负荷需求”的场景。

(a) 若投资前后电价J′=J，则该项投资的增量净效益ΔBt计算公式可简化为：

ΔBt=τmax(Plt-Plt′)J+η(QENSt′-QENSt)Jet-
Tt′-δyTzt′

(19)

式中：右边第一、二项目即为降损效益、可靠性提升效益，第三、四项目即为投资运维成本。

因此，对于现状网架较为成熟、供电能力能满足未来负荷需求且着重提升供电可靠性、降低线损率的配电网规划项目，采用式(19)简化模型计算单个方案的增量净效益和净现值等指标，可真实反映项目的投资收益，进而从成本效益角度决策是否执行该项目。

对于均可执行的各备选方案，ΔBt所得净现值最大者为最优方案，这等同于不采用“有无对比法”直接比较各备选项目的成本，其最小的方案即为最优方案，与常规LCC模型比选结果一致。

(b) 若投资后电价增值(供电质量绩效)，则该项投资的增量净效益ΔBt：

ΔBt=TmaxtPmaxt(J′-J)-[Tt′+δyTzt′+τmax×
(Plt′J′-PltJ)+η(QENSt′-QENSt)Jet]

(20)

对于可执行的多个备选方案，若考虑供电质量绩效电价增值因素，则以式(20)计算所得净现值最大者应为推荐方案，这可能与LCC最小化比选结果不一致。

② 场景二：CA0、CA-2和P′-2构成“现状网架供电能力尚能满足一定阶段的负荷需求但局部尚需新建改造”的场景。

常规成本效益计算中的增供电量收入主要是采用“前后对比法”，这涵盖了存量资产的贡献，无形扩大了一项投资的效益。文献[15]给出了一种基于增供电量收入分摊的思路，但其中增量电量效益、降损效益用“前后对比法”而可靠性提升效益用“有无对比法”互相交叉，尚有不妥之处。

③ 场景三：CA0、CA-3和P′-3构成“当前负荷水平已接近或超过现状网架供电能力、配电网需不断新建和完善”或“新建区域纯增量配电网”的场景。

(a) 对于“当前负荷水平已接近或超过现状网架供电能力”的情况，“无项目”负荷、线损和缺供电量按恒值处理。若投资前后电价J′=J，则该项投资的增量净效益ΔBt：

ΔBt=ΔRt-(Tt′+ΔCyt+ΔClt+ΔCet)=
Tmaxt(Pt′-P)J-[Tt′+δyTzt′+τmax×
(Plt′J′-PlJ)+η(QENSt′-QENS)Jet]

(21)

基于“有无对比法”的分析结果与“前后对比法”一致。

(b) 对于“新建区域为纯增量配电网”的情况，“无项目”所有因素均为0，则一项投资的增量净效益ΔBt计算公式可简化为：

(22)

对于均可执行的多个备选方案，若忽略供电质量绩效电价增值影响，各方案电量收入均相同，那么效益最大的方案其成本最小，与常规LCC模型比选结果一致；当考虑电价影响时，净效益最大者为最优方案，可能与常规LCC模型比选结果不一致。

1.4.2动态经济评估指标

动态经济指标主要包括净现值、净现值率、内部收益率和动态投资回收期。

(1) 增量净现值。考虑有、无项目计算期末设备残值，则增量净现值ΔVNPV：

(23)

式中：i为基准折现率；S′，S分别为第t年有、无项目时中压配电网计算期末的残值。

净现值大于0，方案财务上可行。

(2) 增量净现值率。增量净现值率ΔrNPVR公式如下：

(24)

(3) 增量内部收益率。增量内部收益率ΔrIRR公式如下：

(25)

内部收益率大于基准收益率，方案可行。

(4) 动态投资回收期。动态投资回收期tdpp公式如下：

(26)

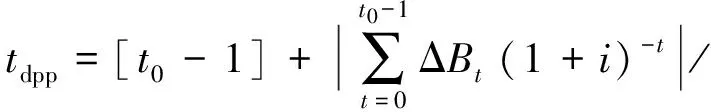
(27)

式中：t0为累计净现值开始大于0对应的年份。

(5) 方案推荐。在多个财务上可行的方案中，可根据决策者偏好选取净现值或净现值率最大的方案为推荐方案。

2　案例分析

2.1　基本参数

某规划区域现状年10 kV网供负荷80 MW，10 kV线路30条，平均负载率约33%，满足N-1供电能力约120 MW。未来各年10 kV网供负荷预测值见表1。

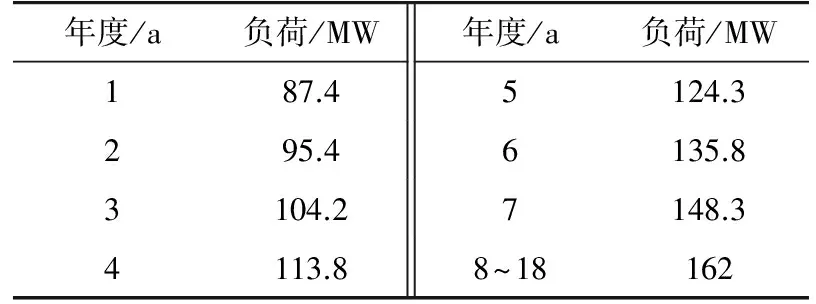
表1　规划区域10 kV网供负荷Tab.1　Load prediction of 10 kV network

最大负荷利用小时数Tmaxt年均4000 h，最大损耗小时数τmax为3000 h，年负荷率η为46%；运维成本率δy为4%～7%，浴盆曲线时间节点为第6年和第14年；单位停电损失成本Jet为10 元/(kW·h)；折现率i为8%。

2.2　供电可靠性指标计算分析

2.2.1现状电网可靠性诊断

搜集、整理所在区域基础参数与可靠性参数，采用故障模式后果分析法计算现状中压配电网供电可靠性指标，见表2。

表2现状年供电可靠性指标
Tab.2Power supply reliability in the basic year

可靠性指标现状平均停电频率/[次·(户·a)-1]3．495平均停电时间/[h·(户·a)-1]35．04供电可靠率/%99．6缺供电量/[(MW·h)·a-1]371．8

该中压配电网老旧、高损及存在安全隐患设备比例约30%，主干线路分段偏少，单辐射线路比例35%，不满足N-1校验线路比例约45%，无配电自动化。

2.2.2方案拟定与可靠性计算

结合区域负荷增长需求、可靠性薄弱环节分析和规划预期目标，统筹解决配网结构优化与存量问题，拟定三种新建改造方案。

(1) 备选方案分年度投资。各备选方案分年度初始投资见表3。方案一、方案二和方案三总建设投资分别为1.151 2亿元、1.496 5亿元和1.726 7亿元。

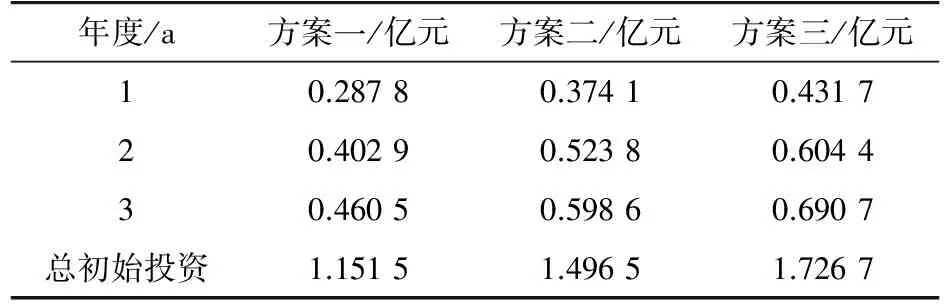
表3　分年度初始投资Tab.3　Annual initial investment

(2) 备选方案分年度供电可靠率。基于故障模式后果分析法计算各备选方案年度供电可靠率，结果见表4。规划水平年(第4年)方案一、方案二和方案三供电可靠率分别为99.91%、99.93%和99.95%。

(3) 规划水平年可靠性指标。规划水平年各备选方案供电可靠性指标见表5。其中，方案一、方案二和方案三的平均停电时间分别比现状年减少27.2 h/(户·a)、28.9 h/(户·a)和30.7 h/(户·a)。

表5规划水平年供电可靠性
Tab.5Power supply reliability in planning level year

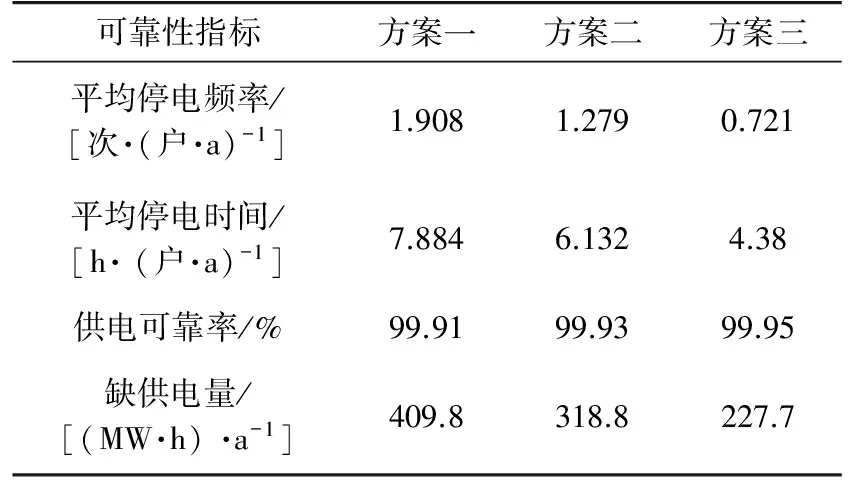
可靠性指标方案一方案二方案三平均停电频率/[次·(户·a)-1]1．9081．2790．721平均停电时间/[h·(户·a)-1]7．8846．1324．38供电可靠率/%99．9199．9399．95缺供电量/[(MW·h)·a-1]409．8318．8227．7

(4) 线损率。经潮流计算，现状、方案一、方案二和方案三10 kV配电网线损率约8%、7%、6.3%和5.6%。

2.3　备选方案成本效益分析

2.3.1基于LCC模型的方案总成本现值

基于LCC思路，采用式(28)计算各备选方案的总成本现值，见表6和图5。

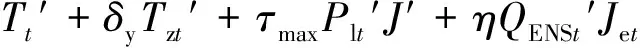
(28)

结合表6和图5，在相同电价和差别电价两种情况下，方案一总综合成本现值最小，为3.303 7亿元，其次是方案二、方案三。由于所有方案中初始投资和运维成本之和占总成本的70%～80%，导致两项费用偏小的方案一综合成本最小。

表6基于LCC模型的各备选方案总综合成本现值
Tab.6Presentvalueofcompositecostfordifferentschemes

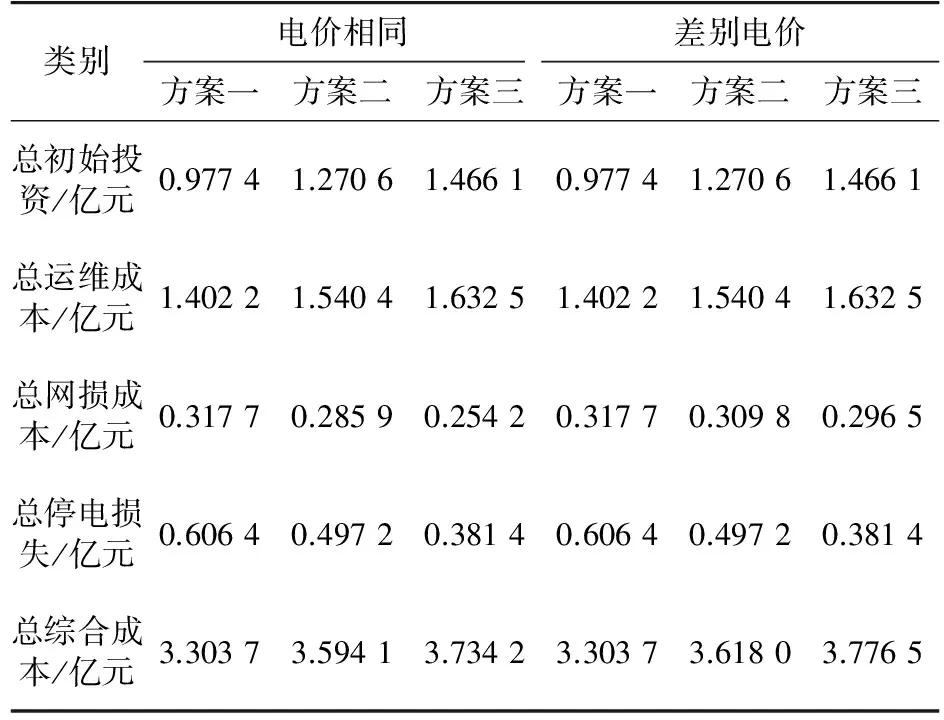
类别电价相同差别电价方案一方案二方案三方案一方案二方案三总初始投资/亿元0．97741．27061．46610．97741．27061．4661总运维成本/亿元1．40221．54041．63251．40221．54041．6325总网损成本/亿元0．31770．28590．25420．31770．30980．2965总停电损失/亿元0．60640．49720．38140．60640．49720．3814总综合成本/亿元3．30373．59413．73423．30373．61803．7765

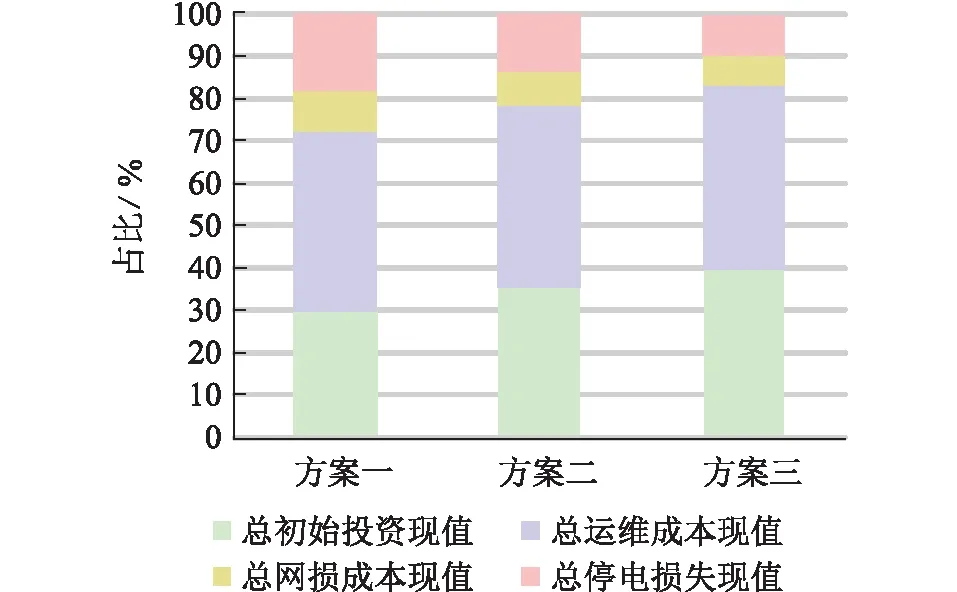
图5　分项成本占比Fig.5　Proportion of subentry cost

2.3.2基于“有无对比法”的方案效益分析

基于“有无对比法”的备选方案经济性评估结果见表7。相同电价时，电价为0.12元/(kW·h)方案一成本优势凸显，其增量净现值最大，为0.6132亿元，其次是方案二和方案三。若考虑供电质量绩效，实施差别电价时,电价分别为0.12、0.13、0.14元/(kW·h)，方案三各项指标最优，其增量净现值最大，为1.148 9亿元，其次为方案一和方案二。

表7备选方案经济评估指标

Tab.7Economic evaluation ndicators of different schemes

类别电价相同差别电价方案一方案二方案三方案一方案二方案三增量净现值/亿元0．61320．32280．18270．61320．80321．1489增量净现值率/%42．617．38．542．643．053．3增量内部收益率/%15．011．19．615．015．617．9动态投资回收期/a11．013．715．311．010．69．6推荐方案方案一方案三

3　结语

本文提出了计及可靠性评估的中压配电网规划方案的形成与比选方法。综合考虑可靠性与经济性，建立基于“有无对比法”给出投资项目的增量净效益，并结合现状网架供电能力与负荷增长需求的不同关系，详细分析多个场景下的净效益简化模型与常规LCC最小化比选方案的异同。根据动态经济指标比选备选方案。案例表明，本文方法有效，对配电网投资决策工作有一定参考意义。

参考文献：

[1] DL/T 1563—2016 中压配电网可靠性评估导则[S].

DL/T 1563—2016 Reliability evaluation guidlines for d￣i￣s￣t￣r￣i￣b￣u￣tion system of medium voltage[S].

[2] 万凌云, 王主丁, 伏进. 中压配电网可靠性评估技术规范研究[J]. 电网技术,2015, 39(4):1096-1100.

WAN Lingyun, WANG Zhunding, FU Jin. Research on technical standard for reliability assessment of medium voltage distribution networks[J]. Power System Technology, 2015, 39(4): 1096-1100.

[3] 宋伟, 万凌云, 张明君. 供电可靠性提升优化策略[J]. 重庆电力高等专科学校学报, 2016, 21(2):16-19.

SONG Wei, WAN Lingyun, ZHANG Mingjun.Optimization strategy of power supply reliability improvement [J]. Journal of Chongqing Electric Power College, 2016, 21 (2): 16-19.

[4] 万凌云, 张盈, 刘真. 配电网供电可靠性薄弱环节分析与改进[J]. 山东电力技术, 2016, 43(6):39-42.

WAN Lingyun, ZHANG Ying, LIU Zhen. Analysis and modification of the weak link of power supply reliability in distribution network[J]. Shandong Electric Power, 2016, 43(6):39-42.

[5] 栗秋华, 刘晋军, 万凌云. 配电网供电可靠性薄弱环节分析[J]. 云南电力技术, 2016, 44 (2):21-22.

LI Qiuhua, LIU Jinjun, WAN Lingyun. Analysis of the weak link of power supply reliability in distribution network [J].Yunnan Electric Power, 2016, 44(2):21-22.

[6] 栗秋华, 万凌云, 徐江涛. 重庆北部新区配电网供电可靠性薄弱环节分析[J]. 四川电力技术, 2016, 39(3):35-38.

LI Qiuhua, WAN Lingyun, XU Jiangtao. Analysis on the weak link of power supply reliability in the distribution network of the northern Chongqing New Area[J]. Sichuan Electric Power Technology, 2016, 39(3):35-38.

[7] 余文辉，王凯琳，高松川. 供电可靠性关键指标分析方法及应用[J]. 广东电力，2017，30(7):121-125.

YU Wenhui, WANG Kailin, WANG Songchuan. Analysis method for critical indicators of power supply reliability and its application[J]. Guangdong Electric Power，2017，30(7):121-125.

[8] 万凌云, 王主丁, 庞祥璐. 中压配电网可靠性评估参数收集及其规划应用[J]. 供用电, 2017, 34(6):38-43.

WAN Lingyun, WANG Zhuding, PANG Xianglu. Parameter collection and planning application of medium voltage distribution system reliability assessment [J].Distribution & Utilization, 2017, 34(6):38-43.

[9] 王凯军,孙飞飞,兰洲,等. 全寿命周期成本管理在实际电力网络规划中的应用[J]. 电力建设, 2016, 37(4): 43-49.

WANG Kaijun, SUN Feifei, LAN Zhou, et al. Application of life cycle cost management in network planning of actual power system[J]. Electric Power Construction, 2016, 37(4): 43-49.

[10] NILSSON J, BERTLING L. Maintenance management of wind power systems using condition monitoring systems-life cycle cost analysis for two case studies[J]. Energy Conversion IEEE Transactions on, 2007, 22(1):223-229.

[11] 杨金涛, 乐健, 刘开培,等. 基于LCC的配电网供电电压质量改善措施的优化[J]. 电力自动化设备, 2015, 35(8):59-64.

YANG Jintao, LE Jian, LIU Kaipei, et al. Improvement measure optimization based on LCC for voltage quality of distribution network[J]. Electric Power Automation Equipment, 2015, 35(8):59-64.

[12] 王卫平. 基于全寿命周期成本—效益模型的增量配电网投资风险评估[J]. 广东电力，2017，30(9):45-51.

WANG Weiping. Evaluation on investment risk of incremental power distribution network based on full life cycle cost and benifit model[J]. Guangdong Electric Power，2017，30(9):45-

51.

[13] 周伟民, 李成, 丁慧. 基于全寿命周期的35 kV电网规划方案SEC比选方法[J]. 电子技术与软件工程, 2017(2): 243-244.

ZHOU Weimin, LI Cheng, DING Hui. The 35 kV network planning scheme SEC comparison method based on LCC[J]. Electronic Technology & Software Engineering, 2017 (2): 243-244.

[14] 刘晓燕. 基于全寿命周期管理的电力设备状态检修成本研究[J]. 电力工程技术, 2016, 35 (5):74-76.

LIU Xiaoyan. Research on state maintenance cost of power equipment based on life cycle management [J]. Electric Power Engineering Technology, 2016, 35(5): 74-76.

[15] 闫敏, 李红霞, 张媛. 基于全寿命周期的投资效益评估方法[J]. 电网技术,2014, 38(s1):48-52.

YAN Min, LI Hongxia, ZHUANG Yuan. Research of investment post-evaluation methods based on life cycle[J]. Power System Technology, 2014, 38(s1): 48-52.

[16] 杨江, 宣伟锡, 姜念. 基于全寿命周期的城市电力管沟规划建设模式研究[J]. 电力工程技术, 2016, 35(3):34-38.

YANG Jiang, XUAN Weixi, JIANG Nian. Research on urban power pipe ditch planning and construction based on LCC [J]. Jiangsu Electrical Engineering, 2016, 35 (3): 34-38.

[17] 国家发改委.省级电网输配电价定价办法发改价格([2016] 2711号)2016.

National Development and Reform Commission. Pricing method of transmission and distribution for provincial power grid ([2016] 2711) 2016.

[18] 王绵斌,谭忠富,张蓉. 基于“增量法”下的电网投资风险评估模型[J]. 电工技术学报, 2006, 21(9):18-24.

WANG Mianbin,TAN Zhongfu,ZHANG Rong, et al． Risk evaluation model of the power grid investment based on increment principle [J]. Transactions of China Electro Technical Society,2006,21(9):18-24．

[19] 关沛, 李智勇. 基于“有无对比法”的城市电网规划项目的经济性分析[J]. 陕西电力, 2009, 37(10):92-96.

GUAN Pei, LI Zhiyong. Economic analysis of urban power network planning projects based on with & without comparison evaluation method[J]. Shaanxi Electric Power, 2009.