模块化多电平换流器直流双极短路故障耐受能力研究

朱铭炼， 姜田贵， 欧阳有鹏，谢晔源

(南京南瑞继保电气有限公司，江苏 南京 211102)

0　引言

目前，模块化多电平换流器(modular multilevel converter，MMC)技术已经成功应用于上海南汇直流输电示范工程、浙江舟山多端柔性直流输电示范工程、广东南澳多端柔性直流输电示范工程、厦门柔性直流输电科技示范工程等多个柔性直流输电工程中[1-3]。世界上第一个基于MMC技术的统一潮流控制器UPFC(unified power flow controller，UPFC)工程也在南京西环网220 kV UPFC工程中成功应用，提升了区域供电能力[4]，而2018年底正式投运的苏南500 kV UPFC工程则是世界上电压等级最高、容量最大的UPFC工程，将在世界范围内首次实现500 kV电网潮流的灵活、精准控制[5-6]。

直流双极短路故障是MMC最具严重后果的故障之一，针对MMC的直流双极短路故障耐受能力开展研究，对MMC系统电气设计和保护设计具有重要的实用工程价值。从国内外研究现状来看，现有文献着重于MMC双极短路故障电流的暂态分析[7-10]，而对MMC在双极短路故障过程中的耐受能力分析均未见涉及。

本文对MMC直流双极短路故障耐受能力进行研究，首先对MMC闭锁后的故障回路进行理论分析并建立电路模型，给出核心器件所承受的故障电流分配计算方法；其次利用制造商提供的器件参数对器件故障期间的损耗进行计算，并给出瞬时结温计算方法，校核直流双极短路故障耐受能力；然后应用MATLAB搭建仿真模型并通过背靠背试验系统对核心器件的故障电流分配及结温计算方法进行了验证。仿真和试验结果表明，本文所提分析和计算方法准确可行，为实际工程中MMC直流双极短路故障耐受能力的校核和器件选型提供了理论基础。

1　MMC工作原理

1.1　MMC基本结构

图1(a)所示为苏南UPFC工程所采用的三相MMC主电路拓扑结构示意图，换流器包含6个桥臂，每个桥臂由n个相同的半桥型子模块(SM)及一个换流电抗器串联组成。子模块的结构如图1(b)所示，由2个绝缘栅双极型晶体管(IGBT)T1和T2、2个反向并联二极管D1和D2、子模块电容C、保护晶闸管SCR、旁路开关K以及均压电阻R组成。子模块的保护晶闸管SCR用于故障时分担流经二极管D2的暂态电流，而旁路开关K用于子模块故障时的快速切除。

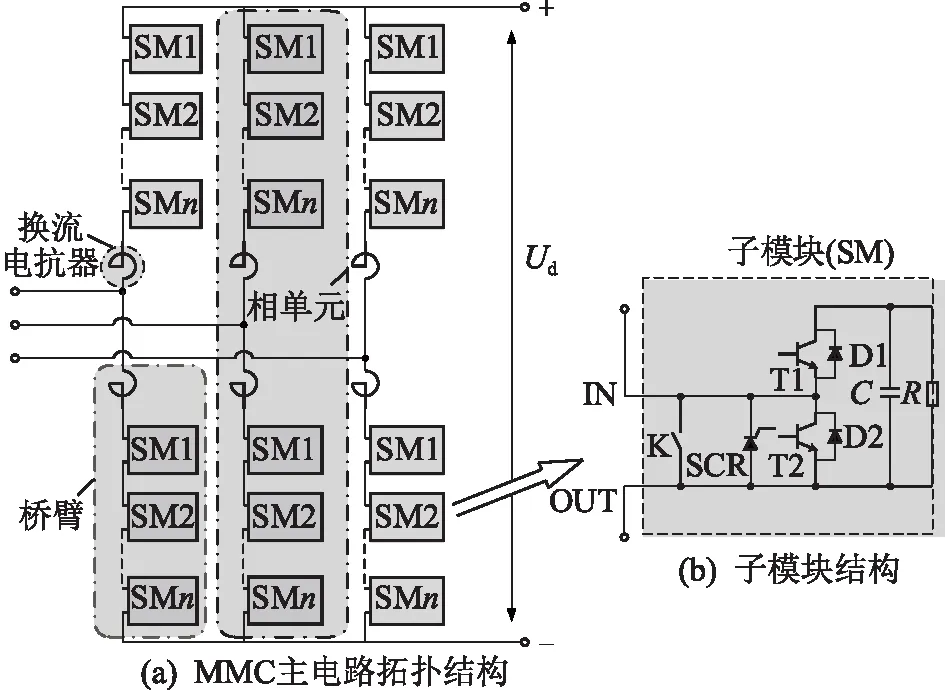
图1　MMC基本结构Fig.1　Basic structure of MMC

MMC桥臂中的每个子模块均为独立控制，每个相单元中上、下两个桥臂的电压和等于直流母线电压，在任意时刻相单元中投入的子模块总数为固定值n，从而维持直流电压的恒定。

1.2　MMC直流双极短路故障机制

在直流侧发生双极短路故障时，MMC承受的故障电流是交流短路电流和子模块电容放电电流的叠加：一部分是交流系统通过子模块的二极管D2向短路点注入短路电流，形成三相短路，电流通路如图2中虚线所示；另一部分是MMC中投入的子模块通过上管IGBT T1放电，放电回路如图2中点划线所示[11]。

图2　直流双极短路时的故障电流回路Fig.2　Path of short-circuit current at the fault of pole-to-pole situation

当MMC的控制保护系统在故障发生几毫秒后检测到系统故障时，MMC立即闭锁，子模块的电容停止放电，但是交流系统注入回路依然存在，直到交流系统的进线断路器成功分闸。

2　直流双极短路故障耐受能力分析

2.1　双极短路故障闭锁后的电流回路

MMC闭锁后，由于IGBT反并联二极管D2为不控器件，无法进行关断，而与D2并联的保护晶闸管的通态电阻小于二极管D2的通态电阻，故在系统发生直流侧短路故障后，触发导通与D2并联连接的保护晶闸管，可以对流过二极管D2的故障电流进行分流，从而实现保护D2的作用。因此，研究MMC直流双极短路故障耐受能力，首先对二极管和保护晶闸管的电流分配关系进行分析。

以单相为例，MMC闭锁后的等效电路如图3所示。MMC闭锁后承受的故障电流为交流系统馈入电流(图3中虚线)和子模块电容放电回路中电感电流续流(图中点划线)两个回路构成。

图3　MMC闭锁后单相电流回路Fig.3　Single phase circuit of MMC after blocking the converter

图中：usa表示交流电源相电压；Zeq交流电源与MMC之间的等效阻抗；Zqb是MMC单个桥臂的等效阻抗；Dup是上桥臂中所有子模块的下部二极管D2；Ddown是下桥臂中所有子模块的下部二极管D2。

保护晶闸管投入后，流过MMC中子模块的故障电流回路如图4所示。

图4　MMC闭锁后子模块的故障电流回路Fig.4　Single phase circuit of sub-module after blocking the converter

2.2　器件电流分配

MMC闭锁后流经换流阀的双极短路故障电流为：

(1)

式中：iup为换流阀闭锁后的双极短路故障瞬时电流；Is为交流系统馈入电流的幅值；Ic为MMC闭锁时刻子模块电容放电回路的瞬时电流值，即电感电流续流回路的电流初始值；ωn为工频角频率；φ为MMC闭锁时刻交流系统馈入电流的初相角；τ为电感电流续流回路的时间常数；td为MMC闭锁后交流系统进线断路器的分闸时间。

MMC闭锁后流经换流阀的双极短路故障电流波形如图5所示。

图5　MMC闭锁后的故障电流波形Fig.5　Current of MMC after blocking the converter

从二极管和保护晶闸管的数据规格书中可以获取特定条件下器件的通态压降V-I特性曲线，二极管和保护晶闸管可以用串联的通态电压偏置、通态电阻以及理想开关来代替[12-15]，采用下述线性拟合并提取二极管和保护晶闸管的V-I特性参数。

(2)

式中：vD,vSCR分别为二极管和保护晶闸管导通期间的通态电压；iD,iSCR分别为二极管和保护晶闸管导通期间流过的电流；rD,rSCR分别为二极管和保护晶闸管的通态电阻；VD0,VSCR0分别为二极管和保护晶闸管的通态电压偏置。

MMC闭锁后，子模块中的二极管和保护晶闸管并联共同承受双极短路故障电流，计算可得二极管和保护晶闸管所承受的电流分别为：

(3)

2.3　二极管和晶闸管的瞬时损耗

二极管和保护晶闸管在MMC闭锁后的损耗主要来自于故障电流通流过程中的通态损耗，其正向截止损耗、开通/关断损耗可以忽略不计，综合式(2)，可得二极管和保护晶闸管的瞬时损耗为：

(4)

2.4　二极管和晶闸管的双极短路故障耐受能力校核

二极管和保护晶闸管所承受的双极短路故障电流为暂态短路电流，电流峰值可至数十千安，该短路电流产生的损耗积累为热量使二极管和晶闸管内部硅片温度急剧上升[16-17]。针对暂态温升计算，二极管和晶闸管技术手册中均给出了器件暂态温升曲线，以晶闸管为例，其暂态热阻抗曲线如图6所示。

图6　晶闸管暂态热阻抗曲线Fig.6　Transient thermal impedance of thyristor

器件数据规格书中给出的暂态热阻抗表示为：

(5)

可得到二极管和保护晶闸管的结温计算方法如下：

(6)

式中：Tj_D和Tj_SCR分别为二极管和保护晶闸管的结温；PD和PSCR分别为二极管和保护晶闸管的损耗；Zth(j-c)_D和Zth(j-c)_SCR分别为二极管和晶闸管的暂态热阻抗(内部芯片到基板)；Tc_D和Tc_SCR为MMC闭锁时刻二极管和晶闸管的外壳温度。

校核计算得到的二极管和晶闸管结温是否超过半导体的本征温度极限250 ℃，如果任一结温超过本征温度，则MMC无法耐受直流双极短路故障。

3　仿真与试验验证

3.1　建模与仿真验证

本节以ABB HiPakTMIGBT模块5SNA 1￣5￣0￣0￣E￣-3￣3￣0￣305及晶闸管5STP 28L4200为例进行MMC直流双极短路故障耐受能力计算及仿真说明。使用曲线拟合技术，得到下表所示拟合结果(器件技术手册中对应结温125 ℃曲线得到的数据)。

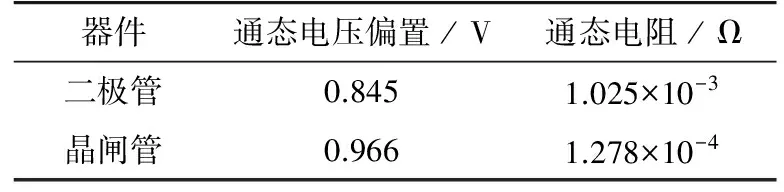
表1　器件通态压降与导通电阻Tab. 1　On-state voltage drop andresistance of thyristor and diode

利用MATLAB/Simulink软件，搭建了MMC闭锁后的子模块故障电流回路仿真模型，验证本文所述MMC双极短路的二极管和晶闸管器件电流分配算法的正确性。在该模型中，设置MMC闭锁时刻桥臂电流峰值为15 kA，其中交流系统馈入电流幅值为7 kA，子模块电容放电电流值为8 kA，设置交流系统进线断路器的分闸时间为100 ms。

图7给出了MMC闭锁后200 ms内的故障总电流、二极管电流、保护晶闸管电流波形的计算波形和仿真波形，计算波形和仿真波形基本吻合，说明本文所提的双极短路器件电流分配计算方法是可行的。

图7　MMC闭锁后的器件计算电流和仿真电流Fig.7　Short-circuit current of diode and thyristor by calculation and simulation after blocking the converter

依据式(6)所述结温计算方法，搭建二极管和保护晶闸管的福斯特网络结温仿真模型，验证二极管和保护晶闸管在MMC双极短路闭锁后承受故障电流时的结温是否安全。设二极管和保护晶闸管外壳初始温度分别为95 ℃和80 ℃，图8是根据式(6)所仿真得到的二极管和保护晶闸管承受双极短路故障电流时的结温情况，根据仿真结果可知，二极管和保护晶闸管最高结温分别为101 ℃和123 ℃，两者结温均安全且有足够的安全裕量，说明MMC能够耐受此双极短路故障电流。

图8　结温仿真结果Fig.8　Simulation results of junction temperature

3.2　试验验证

为了验证文中所提出的MMC直流双极短路故障耐受能力计算方法的正确性，在两端MMC背靠背试验系统中进行了直流侧双极短路试验验证，试验系统直流电压±10 kV，额定容量30 MV·A，二极管以及保护晶闸管为整体封装结构，内部结温无法进行实测，所以试验时测量MMC双极短路故障总电流及保护晶闸管的电流，试验波形如下图所示。

图9　试验波形Fig.9　Test waveforms

试验波形中第一个波头处故障总电流为15.0 kA，保护晶闸管电流为13.9 kA，该电流点处的保护晶闸管分流理论计算值为13.2 kA，二极管分流为1.8 kA，理论计算值与试验实测值基本一致，可见，本文所提MMC双极短路的二极管和晶闸管器件电流分配算法是可行的。

利用文中所提出的MMC双极短路的二极管和晶闸管器件电流分配算法得到的结果与实际试验结果存在微小差异，原因在于：一方面本文采用通态电压偏置、通态电阻进行保护晶闸管及二极管的V-I特性拟合，存在一定的误差；另一方面，考虑实际MMC内二极管和保护晶闸管在工作时，其真实结温小于125 ℃，而本文计算参数中假定的是结温等于125 ℃的情况，计算结果必然存在影响。考虑计算结果与仿真及试验结果差距不大，所以本文所提MMC直流双极短路故障耐受能力校核方法具有较高的工程价值。

4　结语

为了快速有效地进行模块化多电平换流器直流双极短路故障耐受能力校核，本文给出了MMC闭锁后的故障电流回路，并给出了二极管和保护晶闸管的电流分配及结温计算方法。仿真和试验结果表明，所提模块化多电平换流器直流双极短路故障耐受能力校核方法准确有效，对校核模块化多电平换流器在实际工程中的直流双极短路故障耐受能力以及器件选型具有重要的理论指导意义。

参考文献：

[1] 汤广福,庞辉,贺之渊,等. 先进交直流输电技术在中国的发展与应用[J].中国电机工程学报,2016,36(7):1760-1771.

TANG Guangfu, PANG Hui, HE Zhiyuan, et al. R&D and application of advanced power transmission technology in China[J]. Proceedings of the CSEE, 2016, 36(7): 1760-1771.

[2] 胡航海,李敬如,杨卫红,等. 柔性直流输电技术的发展与展望[J]. 电力建设,2011,32(5):62-66.

HU Hanghai, LI Jingru, YANG Weihong, et al. The development and prospect of HVDC flexible technology[J]. Electric Power Construction, 2011,32(5):62-66.

[3] 汤广福,贺之渊,庞辉,等. 柔性直流输电工程技术研究、应用及发展[J]. 电力系统自动化,2013,37(15):3-14.

TANG Guangfu, HE Zhiyuan, PANG Hui, et al. Research, application and development of VSC-HVDC engineering t￣e￣c￣h￣n￣o￣logy[J]. Automation of Electric Power Systems, 2013,37(15):3-14.

[4] 黄志高,潘磊,祁万春,等. 南京UPFC示范工程人工接地短路试验分析[J]. 江苏电机工程,2016,35(6):32-35.

HUANG Zhigao, PAN Lei, QI Wanchun, et al. Analysis of artificial grounding test for Nanjing UPFC pilot project[J]. Jiangsu Electrical Engineering, 2016,35(6):32-35.

[5] 张栋,欧阳有鹏,尚慧玉,等. 电压源型换流阀在绝缘型式试验下电场仿真计算[J]. 江苏电机工程,2017,36(2):25-30.

ZHANG Dong, OUYANG Youpeng, SHANG Huiyu, et al. Electric field simulation and calculation of voltage sourced converter valve in insulation type test[J]. Jiangsu Electrical Engineering, 2017,36(2):25-30.

[6] 李鹏,林金娇,孔祥平,等. 统一潮流控制器在苏南500 kV电网中的应用[J]. 电力工程技术,2017,36(1):20-24.

LI Peng, LIN Jinjiao, KONG Xiangping, et al. Application of UPFC in the 500 kV southern power grid of Suzhou[J]. Electric Power Engineering Technology, 2017,36 (1):20-24.

[7] 徐政,肖晃庆,张哲任,等. 模块化多电平换流器主回路参数设计[J]. 高电压技术,2015,41(8):2514-2527.

XU Zheng, XIAO Huangqing, ZHANG Zheren, et al. Design of main circuit parameters of modular multilevel converters[J]. High Voltage Engineering, 2015,41(8):2514-2527.

[8] 罗雨,饶宏,许树楷,等. 级联多电平换流器的高效仿真模型[J]. 中国电机工程学报,2014,34(15):2346-2352.

LUO Yu, RAO Hong, XU Shukai, et al. Efficient modeling for cascading multilevel converters[J]. Proceedings of the CSEE, 2014,34(15):2346-2352.

[9] 宋强,刘文华,李笑倩,等. 模块化多电平换流器稳态运行特性的解析分析[J]. 电网技术,2012,36(11):198-204.

SONG Qiang, LIU Wenhua, LI Xiaoqian, et al. An analytical method for analysis on steady-state operating characteristics of modular multilevel converter [J]. Power System Technology, 2012,36(11):198-204.

[10] 张哲任,徐政,薛英林. 基于分段解析公式的MMC-HVDC阀损耗计算方法[J]. 电力系统自动化,2013,37(15):109-116.

ZHANG Zheren, XU Zheng, XUE Yinglin, et al. Valve loss calculation of MMC-HVDC based on piecewise analytical formula[J]. Automation of Electric Power Systems, 2013,37(15):109-116.

[11] 王姗姗,周孝信,汤广福,等. 模块化多电平换流器HVDC直流双极短路子模块过电流分析[J]. 中国电机工程学报,2011,31(1):1-7.

WANG Shanshan, ZHOU Xiaoxin, TANG Guangfu, et al. Analysis of submodule overcurrent caused by DC pole-to-polefault in modular multilevel converter HVDC system[J]. Proceedings of the CSEE, 2011,31(1):1-7.

[12] DROFENIK U, KOLAR J W. A general scheme for calculating switching-and conduction-losses of power semiconductors in numerical circuit simulations of power electronic systems[C]. Proceedings of 5th International Power Electronic Conference, 2005, Niigata, Japan.

[13] 薛英林,徐政,张哲任,等. 采用不同子模块的MMC-HVDC阀损耗通用计算方法[J]. 电力自动化设备,2015,35(1):20-29.

XUE Yinglin, XU Zheng, ZHANG Zheren, et al. General method of valve loss calculation for MMC-HVDC with different submodules[J]. Electric Power Automation Equipment, 2015,35(1):20-29.

[14] 王海田,汤广福,贺之渊,等. 模块化多电平换流器的损耗计算[J]. 电力系统自动化,2015,39(2):112-118.

WANG Haitian, TANG Guangfu, HE Zhiyuan, et al. Power losses calculation of modular multilevel converter[J]. Automation of Electric Power Systems, 2015,39(2):112-118.

[15] 李强,庞辉,贺之渊. 模块化多电平换流器损耗与结温的解析计算方法[J]. 电力系统自动化,2016,40(4):85-91.

LI Qiang, PANG Hui, HE Zhiyuan, et al. Analytic c￣a￣l￣c￣u￣l￣a￣ting method for loss and junction temperature of modular multilevel converter[J]. Automation of Electric Power Systems, 2016,40(4):85-91.

[16] 杨俊，汤广福，曹均正,等. HVDC 阀晶闸管结温计算等效电路模型[J]. 中国电机工程学报,2013,33(15):156-163.

YANG Jun, TANG Guangfu, CAO Junzheng, et al. Study on equivalent circuit model for HVDC valve thyristor junction temperature calculation[J]. Proceedings of the CSEE, 2013,33(15):156-163.

[17] 张哲任,徐政,薛英林,等. 基于分段解析公式的MMC-HVDC阀损耗计算方法[J]. 电力自动化设备,2013,37(15):109-116.

ZHANG Zheren, XU Zheng, XUE Yinglin,et al. Valve loss calculation of MMC-HVDC based on piecewise analytical formula[J]. Electric Power Automation Equipment, 2013,37(15):109-116.