牛顿迭代法在草图约束优化问题中的改进

张　龙，卫琛戈，常　伟，张睿航，钟　岩

(西北工业大学 理学院，陕西 西安 710129)

CAD技术在产品开发或是科研中的作用愈来愈重要，实际应用中人们一般将CAD草图的几何约束条件转化为非线性方程组进行求解。数值计算中求解非线性方程组的方法众多，常用的有牛顿法、Brown等[1-4]。牛顿法因解决此类问题具有速度快等优良特性，而得到了广泛的应用。然而，此法要求给定的初值与精确解应充分靠近，常因难以给定满足收敛条件的初值x(0)而造成计算失败[5-7]。因此，基于牛顿法的初值选取对于草图约束的求解至关重要。

文献[8]中结合了遗传算法来确定采用牛顿法求解草图约束问题时的初值，文献[9]介绍了一种用蚁群算法确定初值的方法。人工蜂群算法是一种以蜜蜂群体生活为背景实现在一定范围内寻找目标问题的最优解的模型，其算法简单、具有较强的全局搜索能力，但收敛速度较慢[10-11]。而牛顿迭代法虽然对初值的选取要求比较高，但是其具有较高的收敛速度。因此，本文将两种算法结合起来，提出了基于蜂群算法的牛顿迭代法来求解草图约束问题，既保证了迭代速度，又避免了问题求解过程中陷入局部最优值，提高了问题求解的成功率和求解速度，从而有效解决CAD草图约束问题。

1　模型的建立

对于草图几何约束问题，其约束条件能够被转化为如下含有m个方程的n元非线性方程组的一般形式

(1)

在采用牛顿迭代法求解方程组(1)时，为了在精确解附近选取一个合适初值来确保迭代收敛，文中使用人工蜂群算法对其进行初步探索。将方程组(1)转化为适用于蜂群算法的单个目标方程

|f1(x)|+|fx)|+…+|fm(x)|=0

(2)

显然，方程(2)在最小值取到0时与方程组(1)是等价的。以方程(2)为基础构造目标函数

G(x)=|f1(x)|+|f2(x)|+…+|fm(x)|

(3)

故对方程组(1)的牛顿法初值的选取问题转化为利用人工蜂群算法求解目标函数(3)的极小值问题。当求解出方程(3)的最优解之后，同时得到了牛顿法的合适初值，草图约束问题求解成功。

2　基于人工蜂群的牛顿迭代算法

2.1　牛顿法

牛顿迭代法[12-13]求解非线性方程组(1)本质上是将每一个子方程fi(x)对多个变量用泰勒展开进行线性近似表示。设方程组(1)存在解x*，且在x*的某个开邻域D0内可微，则

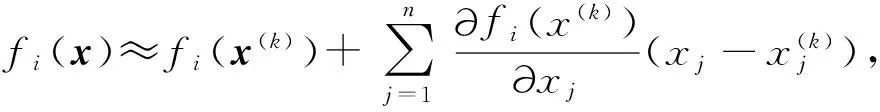
(4)

其中x(k)∈D0是方程组(1)第k次近似解。于是可用方程组

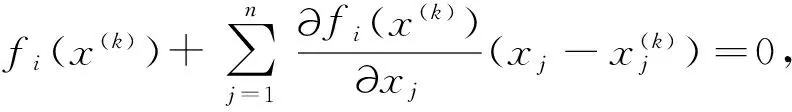
(5)

即

F′(xk)(x-x(k))=-F(x(k))

(6)

近似代替非线性方程组(1)，并将线性方程组(6)的解作为式(1)的第k+1次近似解，从而得到牛顿迭代公式

x(k+1)=x(k)-[F′(x(k))]-1F(x(k)),k=0,1,2,…

(7)

接下来进行人工蜂群算法在牛顿迭代法初值选取上的探索。

2.2　人工蜂群算法

蜂群最小搜索模型的基本要素有食物源、引领蜂、跟随蜂以及侦察蜂。食物源即为目标问题的可能解。引领蜂先去寻找食物源并记录下花蜜的数量，即对应解的“适应度”，反映这个可能解的优劣程度；跟随蜂获取到引领蜂传回的标记食物源的花蜜信息后，根据花蜜信号强度选择优食物源，花蜜信号强度越强，则食物源越容易被选取。然后对该食物源的领域进行搜索，并记录最优的食物源。若某个食物源被遗弃，则应由侦查蜂随机寻找新的食物源。

设方程组(1)含有d个参数，利用蜂群算法求解迭代式(7)的初值，即式(3)的极小值[14-15]。

假设人工蜂群算法求解得到SN个初始解(即得到SN个食物源)，每个解xi(i=1,2,3,…,SN)是一个d维向量。首先，引领蜂对所有食物源进行循环搜索，次数为C(C=1,2,3,…,MCN)。记录每个食物源的花蜜量(计算适应度)

(8)

其次，引领蜂对所有食物源(解)进行一次领域搜索

vij=xij+φij(xij-xkj)

(9)

其中，j∈{1,2,…,d},k∈{1,2,…,SN}，且k≠i。φij是[-1，1]之间的一个随机数，其决定着xij领域的范围大小，且该范围随着搜索越靠近最优解会逐渐减小。

对上述领域搜索结果再次进行适应度计算，若寻找到的新食物源(解)具有的花蜜信息强度(适应度)强于之前的食物源所具有的花蜜信息强度，则用新的食物源代替旧的食物源；反之，则依旧以旧食物源为最优食物源。当所有引领蜂对所有食物源进行搜索后，引领蜂将每个食物源的花蜜信息强度传递给跟随蜂，跟随蜂根据花蜜信号强度以一定的概率Pi选择食物源，其中

(10)

由式(10)可以看出，当食物源所具有的花蜜信号越强时，其被选中的概率越大。跟随蜂根据花蜜信号强度选定食物源后，利用式(7)对食物源的领域进行搜索，并根据花蜜信号强度择优选中最优食物源。

(11)

随机获得一个新的解来替代xi。通过反复搜索，不断优化解，得到最终解。其将作为牛顿迭代法的初值进行迭代得到最优解。

2.3　混合算法的流程

采用基于蜂群算法的牛顿迭代法求解草图约束优化问题的步骤如下：

步骤1初始化，在给定范围内随机给定初始解为xi(i=1,2,…,SN)，设置最大循环次数MCN，参数MD；

步骤2根据目标函数计算获取每个解的适应度，同时引领蜂通过式(9)对该解的领域进行搜索，得到新的解vi，并计算得到新解的适应度；

步骤3判断vi的适应度是否大于xi的适应度，若大于，则用vi替代xi，将vi作为当前最优解。否则，保留xi不变；

步骤4通过式(10)计算获取解xi的概率值Pi；

步骤5跟随蜂依据Pi大小，选择食物源(解)，同时根据式(9)对解的邻域进行搜索得到新的解vi，并计算其适应度值；

步骤6进行贪婪选择，同步骤3；

步骤7判断是否存在被遗弃的解。若有，则根据式(3)产生新的解xi来代替它；

步骤8保存目前适应度值最优的解；

步骤9若循环次数大于MD，执行牛顿迭代法，否则返回步骤2，重新搜寻(若再次搜寻时，不用再次随机初始化解，而是从已搜寻到的解的邻域再做搜寻)；

步骤10对步骤8中的解进行牛顿迭代，判断是否满足迭代终止条件。若满足，输出最优解；反之，返回步骤2，(同步骤9，再次搜寻时，不用再次随机初始化解，而是从已搜寻到的解的邻域再做搜寻)。

3　仿真实例分析

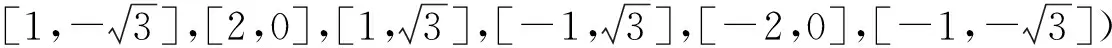
此外，在草图约束求解的实际应用中通常会由于约束改变而导致求解失败。如：修改尺寸、大幅拖动多边形中心、垂直关系转化为平行等。本文以修改正多边形尺寸为例，来探索该算法在稳定性上的表现。

首先，文中随机取出一组仿真结果如表1所示。从表1可看出，基于人工蜂群算法的牛顿法在求解草图约束问题时效果更佳。其中，牛顿法求解正四边形与正六边形草图约束时，边界出现了扭曲且未与坐标轴平行的情况，具体边长大小不符合实际要求。而基于人工蜂群算法的牛顿法给出了更为精确的结果，具体仿真对比数据如表2所示(注：因在实际求解中通常是在求解失败后再次求解直到成功，故计算两种算法平均迭代时间时均统计所有仿真实验消耗时间)。

可以看出，混合算法的成功率得到显著提高。至于平均迭代时间，在简单问题(如正四边形)中牛顿法要小于混合算法，对于较复杂的情况(如正六边形)，混合算法耗时更短。这是因为混合算法在进行全局搜索初值时耗费了较多时间，而对于较为简单的问题这似乎是多余的。经过多次仿真实验证明，对于复杂问题，混合算法在迭代速度和成功率上有明显优势。

为了进一步探索算法的稳定性，本文扩大多边形尺寸为原先的10倍进行仿真，仿真结果如表3所示。

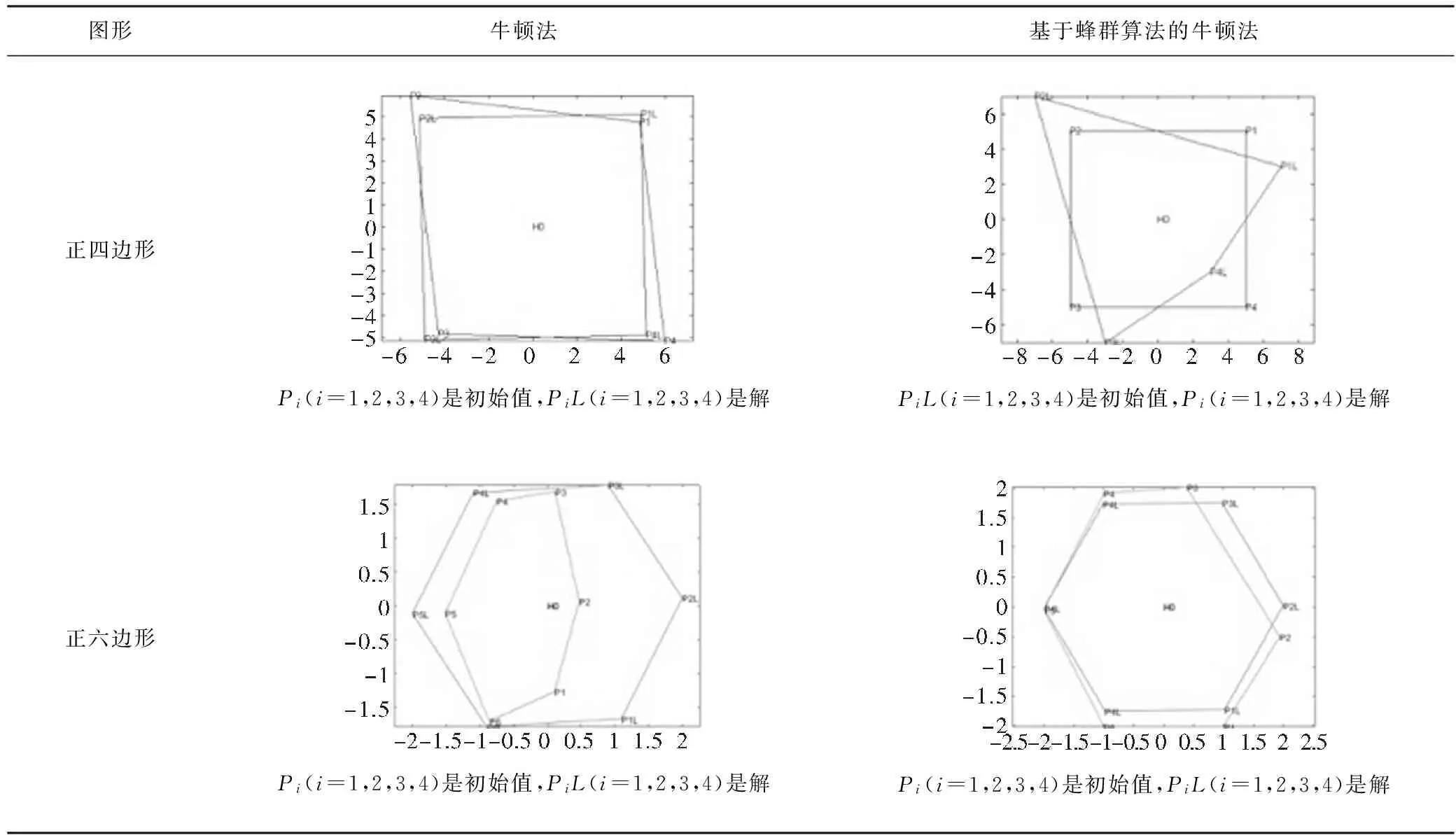
表1　不同算法仿真结果

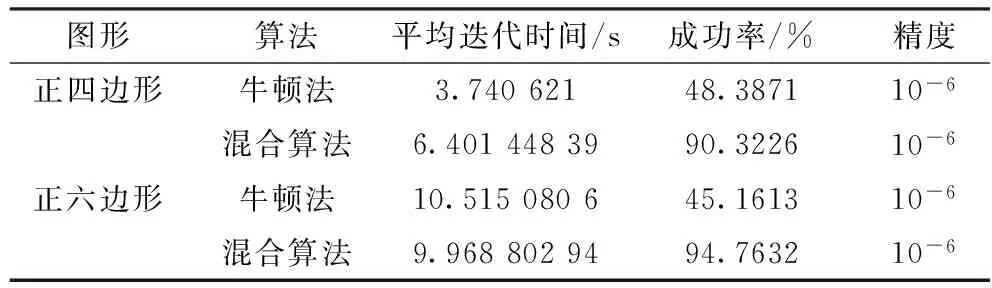
表2　求解不同图形参数对比

表3　扩大10倍正六边形仿真结果

仿真结果显示，混合算法的成功率仍高于90%，但迭代时间表现一般。原因在于对单个几何元素改变尺寸后，解在搜索域内更为稀疏，蜂群算法全局搜索所损耗的资源增加。不过对一些多几何元素多耦合关系的约束问题而言，随着解在搜索域内稀疏程度降低，按一定程度扩大尺寸，混合算法在时间上的优势仍比较明显。

4　结束语

为了快速高效求解草图约束问题，本文将对收敛速度快而初值选取敏感的牛顿法和全局搜索能力强而搜索慢的人工蜂群算法有效结合起来，达到了既提高收敛速度又确保成功率的目的，且优化了算法。该算法对于较为简单的问题虽然迭代时间有所损失，但提高了成功率。仿真实验显示，该算法结果是可靠的，有较强的数值稳定性，是一种不错的求解草图约束问题的方法。

[1]王爱华.遗传算法及其在非线性方程组求解中的应用研究[J].西华师范大学学报:自然科学版,2015,36(2):204-208.

[2]谭振江,肖春英.非线性方程数值解法的研究[J]. 吉林师范大学学报:自然科学版,2014(3):102-105.

[3]刘元文.带凸约束非线性方程组解法的若干研究[D].海口:海南大学,2015.

[4]郭妞萍.求解非线性方程的指数迭代法[J].西安文理学院学报:自然科学版,2015,18(3):31-34.

[5]姚腾腾.基于一致系数求积的广义牛顿法求解非线性方程组[J].厦门大学学报:自然科学版,2016,55(2):221-226.

[6]徐林.基于改进拟牛顿法求解非线性方程组[J].济宁学院学报,2016(6):54-57.

[7]陈飞,王海军,曹苏玉.求解非线性方程组的改进不精确雅可比牛顿法[J].计算机工程与应用,2014,50(14):45-47.

[8]于俊乾.基于偶图和数值方法的几何约束求解算法研究[D].长春:东北大学,2013.

[9]张冰冰,张宏立.求解非线性方程组的蚁群算法[J].工业控制计算机,2013(1):63-64.

[10] 张姣玲,林桂友,许国良.求解非线性方程的混合人工蜂群算法[J].计算机工程与应用,2014,50(10):48-51.

[11] 张姣玲.求解非线性方程及方程组的人工蜂群算法[J].计算机工程与应用,2012,48(22):45-47.

[12] 单吉宁,蔡静.解非线性方程的一类改进型牛顿法[J].湖州师范学院学报,2015(2):9-13.

[13] 陈磊,霍永亮.利用改进的遗传算法求解非线性方程组[J].西南师范大学学报自然科学版,2015(1):23-27.

[14] 胡珂,李迅波,王振林.改进的人工蜂群算法性能[J].计算机应用,2011,31(4):1107-1110.

[15] 刘佳,周真真,夏少芳,等.基于人工蜂群算法的非线性方程组求解研究[J].自动化仪表,2013,34(2):19-22.