自适应标准差特征的压缩感知图像融合
张 烨
(西安科技大学 通信与信息工程学院, 陕西 西安710054)
生活中较常见的两类图像为红外图像和可见光图像,这两类图像由不同的传感器获得,成像机理不同,特点不同[1]。融合红外图像与可见光图像具有较高的研究和应用价值,因此得到了广泛应用[2-3]。目前,图像融合领域中大都以提高图像融合质量为主要考虑因素,而实际生活中,在安全监控、战场感知等应用领域,传感图像大多以动态序列的形式输出,这些系列图像需要被实时地融合处理。若还使用传统的图像融合方法要达到实时处理的效果,不仅实现的复杂度增大,而且很大程度上增加了传输、储存、重构的成本。因此,压缩感知理论(CS理论)[4-5]的引入解决了这个问题。
在基于压缩感知的图像融合算法中,原图像的空间信息在通过CS观测时丢失,因此处理测量系数时不能够使用基于空间的选取规则,复杂的融合规则也无法采用[6]。融合规则大多选择绝对值取大、信息熵加权、相似性度量、标准差加权等简单方法。但由于绝对值取大法得到的融合图像对比度太大,且有明显噪点;信息熵只能笼统计算出包含在观测向量中的信息;相似性度量无法准确得到分类区间而造成分类错误;基于标准差加权得到的融合图像相比之下视觉效果较好,但是,当两幅图像标准差相差不大时,根据系数的权重融合图像很可能导致图像融合效果变差,而使用绝对值取大法则能够获取两幅图像各自瞬变特征的显著信息[7]。因此,本文提出了一种自适应的融合规则,兼顾了待融合图像的背景信息和红外目标信息,有效提高了图像的融合质量。
1 压缩感知的数学模型

(1)
x=ψθ
(2)
其中,ψ=(ψ1,ψ2,…,ψN)∈RN×N为正交基字典矩阵。假设系数向量θ是K阶稀疏的,即其中非零稀疏的个数K≪N,那么采用另一个与正交基不相关的矩阵Φ:M×N(M≪N),对信号X做压缩观测可以得到M个线性投影,其中y∈RM,可表示为
y=Φx=Φψθ=ACSθ
(3)
显然从y中恢复x是一个NP-hard问题,但只要矩阵ACS任意2K列都是线性独立的,那么至少存在一个K-系数的系数向量θ满足y=ACAθ。换言之,在满足上述要求的情况下,通过求解一个非线性优化问题就能从观测y、观测矩阵Φ和字典矩阵Ψ中近乎完美的重建信号X[8-10]。
2 图像融合的基本框架
本文采用非下采样 Contourlet变换(NSCT变换)[11]对待融合图像进行多尺度分解。图像经NSCT变换后被分解为1个低通子带和K个方向子带,由于低频系数不具备稀疏性,而高频系数具有较高稀疏性,所以保留图像低频系数,只对高频系数进行观测;重构时,利用重构算法对高频系数进行恢复,在经过NSCT逆变换重构出图像[12-13]。基于NSCT的压缩感知图像融合框图如图1所示。
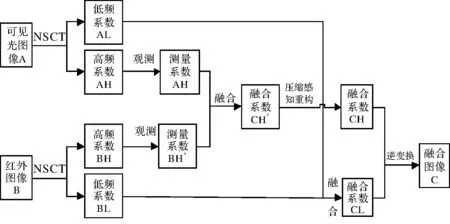
图1 融合框图
2.1 低频系数融合规则
不同物体在红外图像和可见光图像的表达能力不同,可见光图像的中高频信息多分布在背景等处,而红外图像的中高频则分布在热目标处。传统融合算法中,对低频的处理结果往往使背景比较模糊,或者为了突出红外效果而造成背景信息权重偏向红外图像。因此,为得到更佳的融合图像,其背景应多来自可见光图像,热目标信息来自红外图像[14]。根据这个特点,本文选择分块DCT高频能量准则融合NSCT分解得到的低频系数。
(1)对低频系数做DCT分块变换。DCT变换系数矩阵的特点是:中高频分量分散在右下角,低频分量集中在左上角。如果直接计算DCT分块的能量会导致图像的中高频能量被掩盖,而每个子块的副对角线右侧系数基本反映了原图像块的高频信息。因此根据对比每一分块的高频能量选择融合系数。定义DCT变换矩阵高频能量如式(4)所示
(4)
其中,N为图像分块大小,D(u,v)表示DCT系数矩阵中的系数,本文中分为8×8的子块。
图像融合时往往会出现部分灰度均匀的区域,且这些区域通常为背景,如果仅依据DCT系数的高频能量规则融合则易出现误判。因此在融合时,若两幅原图像的DCT高频能量差值小于阈值T时,融合时偏重可见光图像系数,即
XF(i,j)=a×XA(i,j)+(1-a)×XB(i,j),|EA-EB| (5) 其中a=0.8,XF(i,j)为融合后的系数,XA(i,j)和XB(i,j)为两幅原图像的像素。 当差值大于T时,分为两种情况;红外图像量较大,融合系数权值侧重红外图像。 (6) 其中b=0.2,EA和EB分别为可见光图像和红外图像的DCT分块系数矩阵能量。 通常来说,绝对值更大的系数代表更多的瞬变特征显著信息。但是CS观测过程是对原图像的线性投影,得到的观测向量是观测矩阵内系数的线性组合,观测矩阵的随机性使原图像的信息随机分布到观测向量上。当图像包含的信息很多时,绝对值系数大的图像不一定是信息量多的图像,而标准差却能表示图像信息量的多少。因为标准差反应的是灰度动态范围,标准差越大,说明图像灰度级分布越分散,图像的对比度越高,图像包含的信息越多。但是当两幅图像的标准差相差不大时,无法判断哪副图像包含的信息更多[15],系数的权重很可能导致融合效果变差,而使用绝对值取大法则能够获取两幅图像中较大的系数,得到图像瞬变特征的显著信息,提高细节的清晰度。因此,本文采用标准差加权和绝对值取大相结合的图像融合方法。具体步骤如下: (1)分别计算高频分量经过压缩后红外图像和可见光图像的标准差sd,如式(7)所示。 (7) (2)计算两幅观测图像标准差sdA和sdB的差值,如式(8)所示。 sdt=|sdA-sdB| (8) 其中,sdA和sdB为可见光图像和红外图像观测系数的标准差; (3)计算观测后的融合值YF(i,j)。当差值sdt大于阈值T,说明两幅图像包含信息量的差异大,因此融合时要更偏重于标准差大的图像,故采用标准差加权的方式作为融合规则。当差值小于阈值T时,说明两幅图像包含的信息量相差不大,此时,两幅图像的细节信息差异小,因此采用绝对值取大法融合图像,突出其各自的细节信息。具体的融合规则如式(9)所示。 (9) 选择Matlab 2013a为软件仿真工具,实验分析图像均为256×256大小灰度级的可见光图像和红外图像。此外,本文将绝对值取大法(CS_MAX)、信息熵加权法(CS_E)和标准差加权法(CS_SD)以及本文算法分别运用于两组图像,并对融合效果从主观和客观参数两方面进行比较分析。 图像融合实验仿真效果如图2和图3所示。实验分别对两组待融合可见光图像和红外图像作3层NSCT分解。两组融合图中,图2(c)~图2(e)分别是采用绝对值取大法、信息熵加权法、标准差加权法融合后的效果图,图2(e)为本文算法融合后的效果图。从主观角度来看,这几种方法都能够从红外图像中提取到热源信息,并能将可见光图像和红外图像的特性体现到融合图像中。 图2 图1融合仿真实验效果图 对于第一组图像来说,CS_MAX 法虽提取到了红外目标,但图像的细节模糊,融合的效果最差;CS_E次之,因为信息熵只是改善了图像信息的丰富程度,并不能明显提高图像清晰度; CS_SD融合效果相对较好,不仅更精准的提取到红外目标的轮廓,图像的清晰度也有所提高,但是对图像细节的表达不够清楚;而本文算法融合效果在对红外目标轮廓的提取上要更精准于前3种方法,且与周围背景界线划分明确,在显著突出了红外目标(鸭子)的基础上清楚地保留了可见光图像草丛处细节信息,在背景清晰度上要高于这3种算法。 图3 图2融合仿真实验效果图 对于第二组图像来说,CS_MAX、CS_E和CS_SD这3种算法得到的融合图像细节信息均不清晰,如图3(c)~图3(e)中近处凉棚的边缘、草丛以及远处的栅栏都有不同程度的模糊。而本文算法在精准提取红外目标轮廓的基础上,使融合后的背景更接近可见光图像,例如凉棚的颜色、草丛的分枝及远处人物附近的栅栏。因此,本文算法与其他3种算法相比,保留了更多的可见光图像细节信息。 两组图像的4种算法的客观参数比较如表1所示。由表1可知:本文算法的融合效果在E(信息熵)、Ag(平均梯度)、SD(标准差)这几方面指标中均优于其他算法。由于本文算法是根据源图像的性质而选择不同的融合规则进行图像融合,既得到了图像瞬变特征的显著信息,又丰富了图像的信息量,二者兼而有之,使得融合图像从源图像中获取到更多的信息,增强了细节的表现力。 表1 4种算法图像融合客观参数比较 本文将压缩感知算法应用于图像融合领域,针对低频系数和高频系数各自特征采用不同融合规则进行融合。低频融合选择更能突出红外和可见光图像信息特点的分块DCT高频能量准则,高频考虑到传统图像融合规则中的局部信息选取规则不适用CS 的测量处理,因此采用结合高频观测值特点的自适应融合规则融合图像。仿真实验表明,本文算法在更大程度保留可见光图像细节的基础上准确提取到了红外目标信息,提高了融合图像的效果。 [1]李海超,李成龙,汤进,等.热红外与可见光图像融合算法研究[J].计算机科学与探索,2016,10(3):407-412. [2]钱小燕,韩磊,王帮峰.红外与可见光图像快速融合算法[J].计算机辅助设计与图形学学报,2011,23(7):1211-1216. [3]舒久明.一种自适应的红外与可见光图像融合算法[J].电子科技,2015,28(5):24-26. [4]Donoho D L.Compressed sensing[J].IEEE Transactions on Information Theory,2006,52(4):1289-1306. [5]阮涛,那彦,王澍.基于压缩感知的遥感图像融合方法[J].电子科技,2012,25(4):43-45. [6]柳翠寅,罗洪礼,李晓峰.基于压缩感知的红外与可见光图像融合[J].四川大学学报:工程科学版,2014,46(5):89-95. [7]龚紫平.多观测及分块观测压缩感知的图像融合方法研究[D].广州:华南理工大学,2012. [8]焦李成,杨淑媛,刘芳,等.压缩感知回顾与展望[J].电子学报,2011,39(7):1651-1658. [9]邵文泽,韦志辉.压缩感知基本理论:回顾与展望[J].中国图象图形学报,2012,17(1):1-10. [10] 闫迪.基于压缩感知理论的图像重构与图像融合算法研究[D].西安:西安科技大学,2013. [11] 胡玉成,王创新.基于区域方向的NSCT与PCNN图像融合算法[J].电子学报,2014,27(4):30-32. [12] 袁金楼,吴谨,刘劲.基于NSCT与DWT的压缩感知图像融合[J].红外技术,2015,37(11):957-961. [13] 赵学军,刘静.NSST域内基于压缩感知和PCNN的遥感图像融合[J].科学技术与工程,2016,16(14):260-261. [14] 郭明符,奚晓梁.基于局部能量的NSCT域红外与可见光图像融合算法[J].红外与激光工程,2012,41(8):2229-2235. [15] 亓兴兰,胡宗庆,刘健.SPOT-5全色与多光谱遥感影像融合方法比较[J].北华大学学报:自然科学版,2011,12(2):214-218.2.2 高频系数融合规则
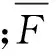
3 仿真结果及分析



4 结束语

