一种面向轮廓保持的轨迹数据压缩算法
孟 庆 彬, 于 晓 强, 刘 柏, 邵 利
( 大连工业大学 信息科学与工程学院, 辽宁 大连 116034 )
0 引 言
近年来,随着具有定位功能的传感器及智能移动终端的兴起,人们可以很方便地获取到个人的移动轨迹。通过对轨迹数据进行分析可以为热点区域发现、城市交通监控、城市功能区识别、城市公共卫生及城市旅游管理等提供支持[1]。但随着用户规模的增大,轨迹数据几乎呈指数增长。有资料表明,北京市有67 000辆出租车,如果这些出租车以2~3 s为周期向数据中心发送位置信息,这些出租车每天就能够产生60 TB的轨迹数据[2]。这些轨迹数据中包含了很多有价值的信息,但海量的轨迹数据也给基于位置的服务(location based service,LBS)带来了挑战:海量的轨迹数据会占用大量的存储空间;海量的轨迹数据会消耗大量的传输流量;当在浏览器中渲染这些轨迹数据时,会给浏览器带来沉重的负担。在地图上渲染1 000个定位点就需要1 s的时间[3],当轨迹数据的规模变大时,难以从轨迹数据中挖掘到有用的知识模式,减少数据的规模能够使得模式挖掘变得相对容易[4]。
轨迹压缩可以分为在线压缩与离线压缩。离线轨迹压缩在进行压缩时,需要轨迹的全部数据。进行离线轨迹压缩时可以充分地利用轨迹的特征,实现精确的压缩。在线轨迹压缩可以在实时地接收轨迹定位点的过程中进行轨迹压缩,具有支持在线应用的优势。一般来说在线轨迹压缩的压缩精度要低于离线轨迹压缩。
离线轨迹压缩算法包括Douglas-Peucker算法[5]、TD-TR算法[6]、最优化的轨迹压缩算法[7-10]、近似最优化的轨迹压缩算法[11]、TS算法[12]、SQUISH-E(μ)算法[13]。在线轨迹压缩算法包括Before-OPW-TR算法[6]、Normal-OPW-TR算法[6]、SQUISH-E(λ)算法[13-14]、SQUISH算法[15-17]。这些轨迹压缩算法能够高效地进行轨迹压缩,但压缩过程中大多没有对轨迹的轮廓进行控制,因而在使用这些算法进行轨迹压缩时易造成轨迹轮廓的丢失。轨迹的轮廓对于描述轨迹的语义起着至关重要的作用。从一个完整轮廓的轨迹中能够详尽地了解到用户去过的地点,在哪些区域或地点进行过停留(停留区域用户的运动方向变化较为频繁,在停留点由于用户的细微移动和定位系统的误差也会导致较大的方向变化),进而可以理解用户的行为。不完整的轮廓会造成曾经到达地点(例如:银行)、停留点(例如:高速公路缴费站、堵车地点)的丢失,不能反映用户在停留区域(例如:公园)的详细的行走路线。没有这些细节,就无法清楚地了解用户的行为,就会造成轨迹语义的丢失。
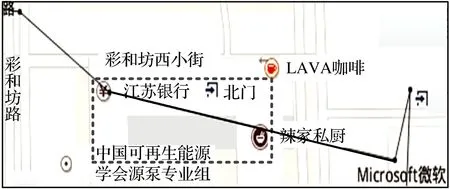
图1针对距离阈值算法,在10 m距离阈值的条件下,展示了一条步行轨迹及其压缩后的表现形式。从图1中虚线框所示的区域可以看出,SQUISH-E(μ)、DP、TD-TR、Before-OPW-TR和Normal-OPW-TR算法均会造成不同程度的轮廓丢失。
为了解决轨迹压缩过程中轮廓丢失的问题,提出了一种面向轮廓保持的轨迹数据压缩算法。该算法使用欧氏距离阈值和角度阈值在开放窗口的过程中对轨迹数据进行压缩。通过设置角度阈值,该算法能够有效地捕捉到单个定位点的方向变化以及窗口内所有定位点方向渐变的情况,从而实现了对轨迹轮廓的控制。
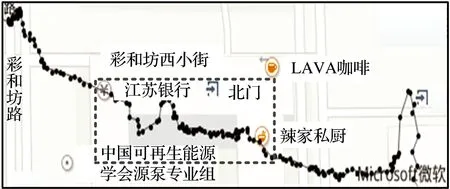
(a) 原始轨迹
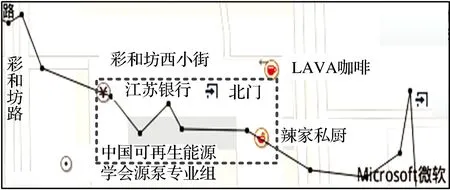
(b) SQUISH-E(μ)算法
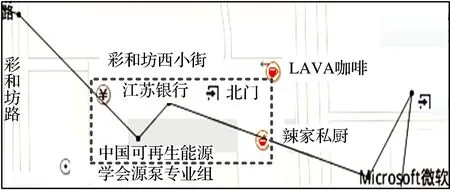
(c) DP算法
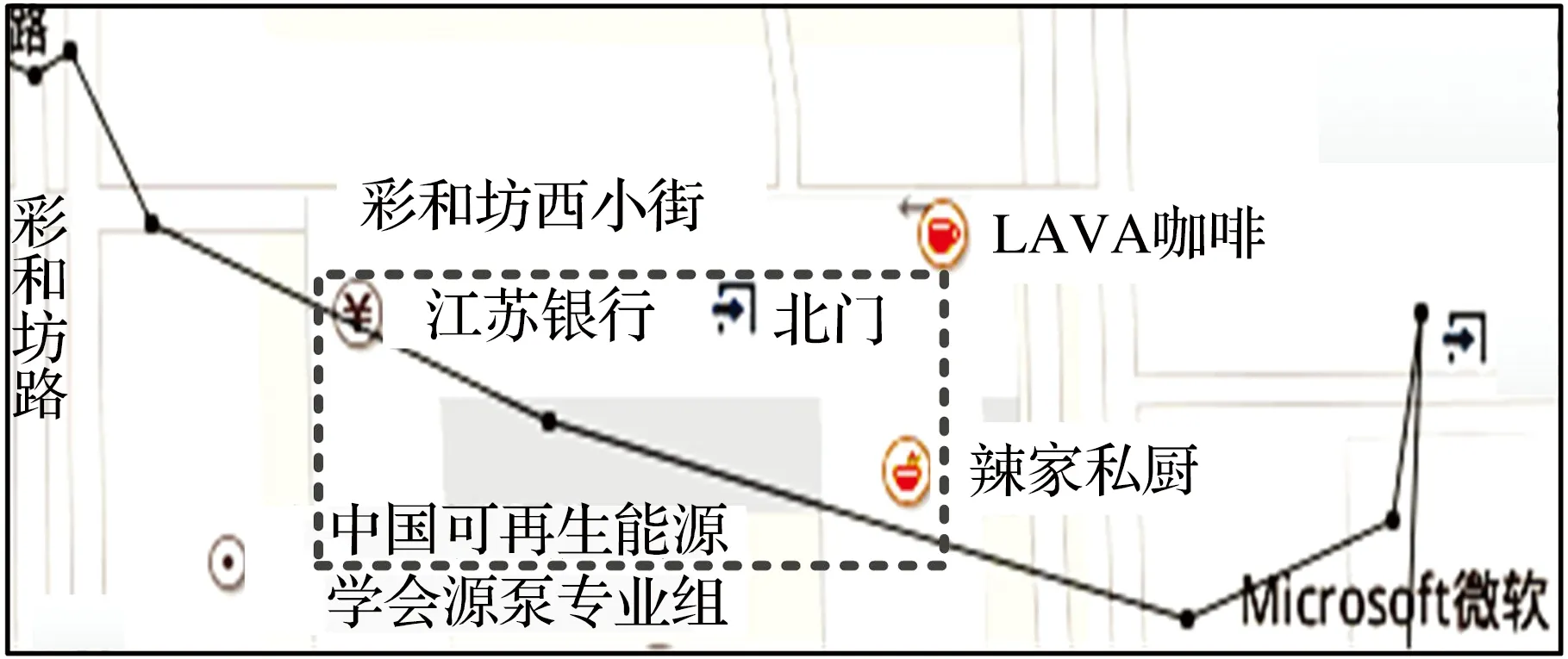
(d) TD-TR算法
(e) Before-OPW-TR算法

(f) Normal-OPW-TR算法
图1一条步行轨迹及其在不同算法10 m阈值压缩后的轨迹
Fig.1A walking trajectory and its 10 m threshold compression trajectories at different algorithms
1 轨迹压缩相关定义
定义1轨迹
一条长度为n的轨迹T是一系列以时间为顺序的定位点的集合,即T={P1,P2,…,Pn-1,Pn}。T中每一个定位点Pi都由三元组(xi,yi,ti)组成,其中xi与yi代表移动对象在ti时刻的位置坐标。
定义2轨迹压缩
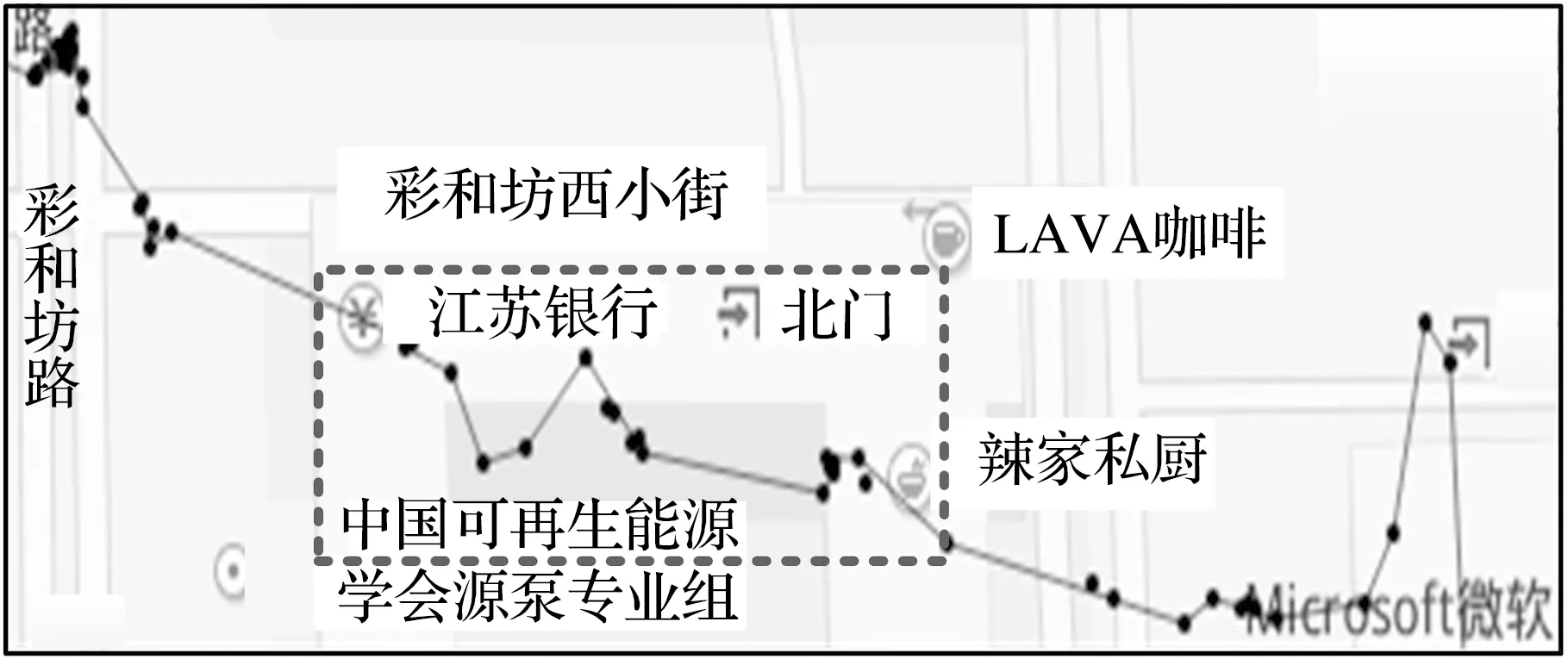
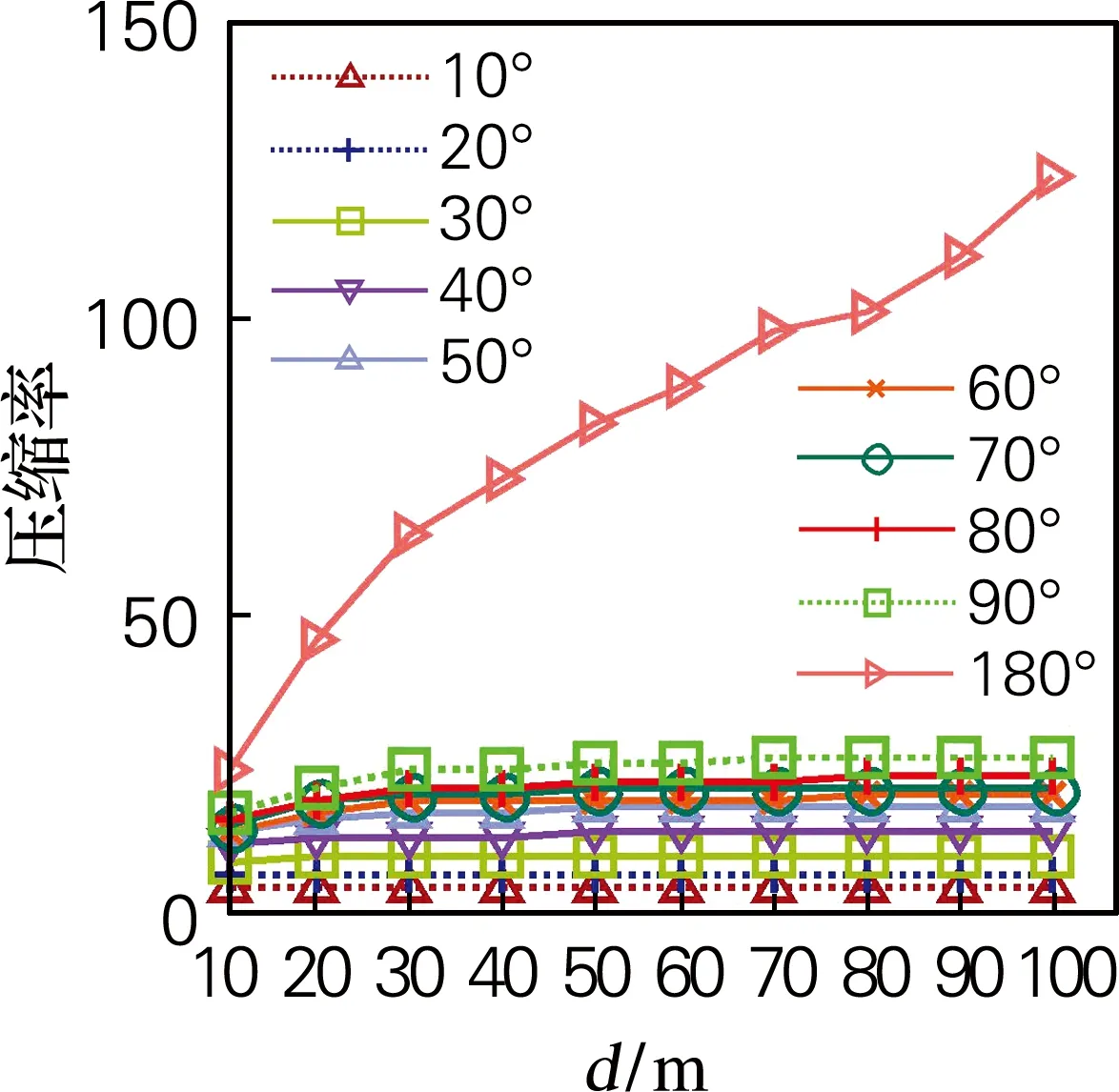
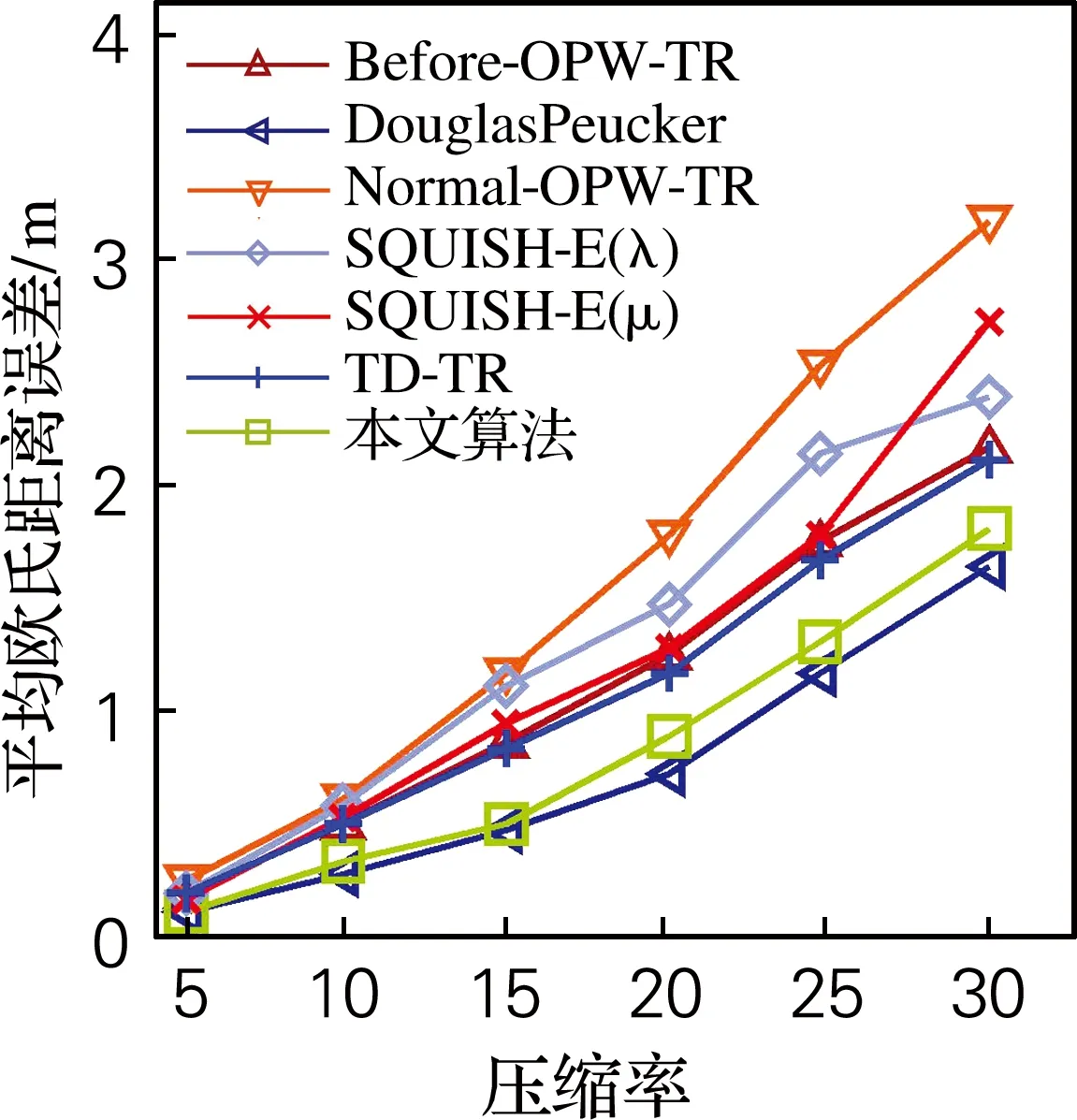
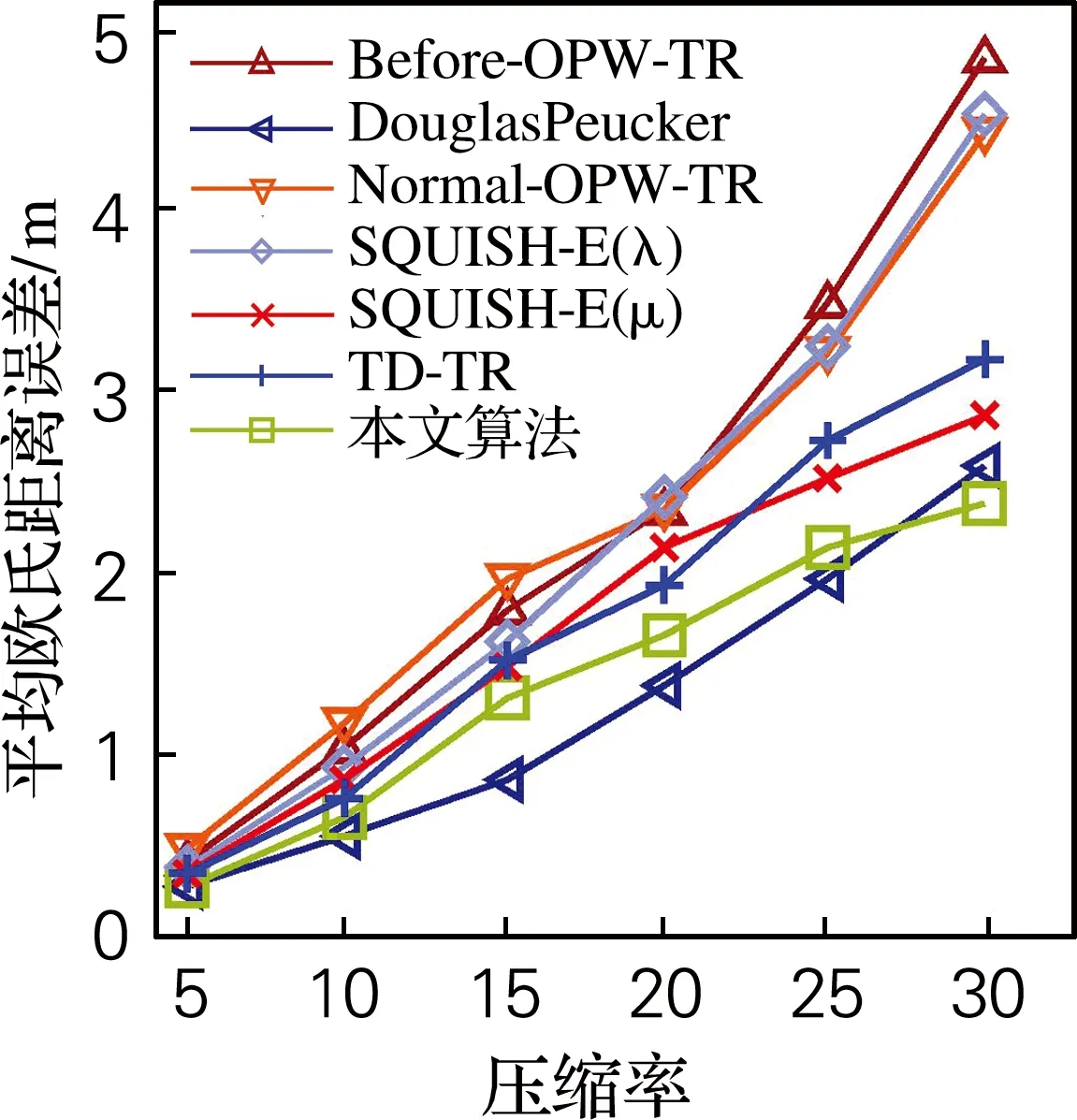
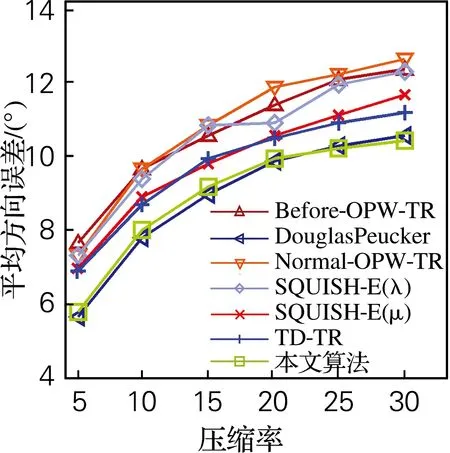
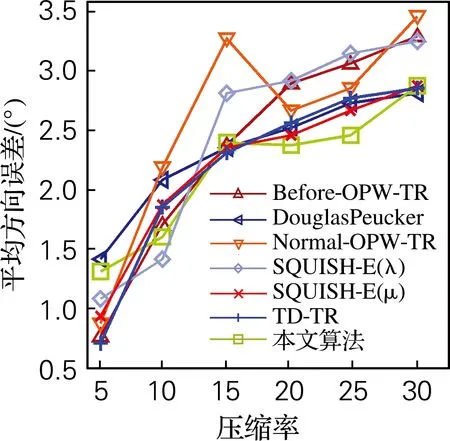
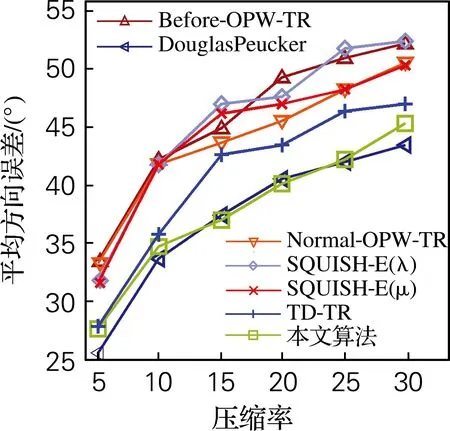
给定轨迹T={P1,P2,…,Pn-1,Pn},轨迹压缩就是要寻找一系列以时间为顺序的定位点的集合T′(T的子集),即T′={Pc1,Pc2,…,Pcm-1,Pcm},其中1=c1 定义3压缩率 给定原始轨迹T={P1,P2,…,Pn-1,Pn},压缩后的轨迹T′={Pc1,Pc2,…,Pcm-1,Pcm}。压缩率 CR=n/m,n≥m (1) 定义4欧氏距离误差 给定原始轨迹T及压缩后的轨迹T′,T中的定位点Pi对应于T′的欧氏距离误差可表示为Pi与Pi的估计点P′i之间的距离。如果T′中包含Pi,则P′i=Pi。否则,P′i为Pi与直线predT′(Pi)succT′(Pi)的垂点,predT′(Pi) 与succT′(Pi)分别表示T′中离Pi最近的前驱和后继。 图2用轨迹T={P1,P2,P3,P4,P5,P6}及其压缩后的轨迹T′={P1,P4,P6}阐述了欧氏距离误差。如图2所示,轨迹T中P1,P4,P6对应于T′的欧氏距离误差为零。P2的欧氏距离误差为P2到直线P1P4的垂直距离。 图2 欧式距离误差 定义5方向误差 给定原始轨迹T及压缩后的轨迹T′,轨迹T中Pi点对应于T′的方向误差可表示为HeadingChange(h1,h2),其中h1为Pi点的方向,h2为T′中的定位点PsPe构成的射线方向。其中,Ps=predT′(Pi+1),Pe=succT′(Pi)。方向变化函数HeadingChange及方向函数Heading定义为 Heading(Pi)=PiPi+1,Pi≠Pn (2) Heading(PsPe)=PsPe (3) HeadingChange(h1,h2)= (4) 给定原始轨迹T,欧氏距离阈值μ和角度阈值θ。在T中的第1个定位点P1及第3个定位点P3之间定义一个窗口,其中P1被称之为锚点Pa,P3被称之为浮动点Pf。执行如下步骤: (1)计算窗口内每一个定位点Pi(除浮动点Pf)到PaPf的欧氏距离及Pi与射线PaPf之间的方向变化。如果任意一个定位点的欧氏距离超过μ或方向变化超过θ,则在该窗口内选择具有最大欧氏距离误差的定位点成为新的锚点,新锚点后的第2个点成为新的浮动点。 (2)如果在该窗口内μ与θ均没有被超过,则进一步判断浮动点的前一个点Pf-1是否为拐点,即判断定位点Pf-2与定位点Pf-1之间的方向变化是否大于θ。如果Pf-1是拐点,则Pf-1成为新的锚点,Pf+1成为新的浮动点。 如果在窗口PaPf之间没有新锚点产生,则浮动点Pf向下移动一个点,在新窗口中重复执行上述步骤。如果产生了新锚点和浮动点,则将上述步骤应用于新锚点与新浮动点构成的窗口。不断地重复这个过程,直到整个轨迹T被压缩为T′。 逐步开放窗口的过程中检查欧氏距离和角度变化,该算法可以确保所有方向变化大于θ的拐点被保留在T′中,同时可以确保窗口内每一个定位点的欧氏距离误差不超过μ,任意两个定位点之间的方向变化不大于2θ。如图3所示,通过设置10 m、60°的阈值对图1(a)中所示的轨迹进行了压缩。结合图1、图3可以看出,相比于其他算法,本文算法能够有效地保留轨迹的轮廓特征。 图3 本文算法的压缩轨迹 面向轮廓保持的轨迹压缩算法如表1所示,算法首先选取P1和P3作为锚点和浮动点(第2、3行)对窗口内的定位点执行步骤1和步骤2(第7行),如果在窗口内没有新的锚点及浮动点产生(即index=1),则浮动点向下移动一个点(第13行)。如果有新的锚点产生,则Pindex和Pindex+2成为新的锚点及浮动点(第10、11行)。当整个轨迹T被压缩完毕后,算法返回压缩后的轨迹T′(第20行)。 表1 面向轮廓保持的轨迹压缩算法Tab.1 Compression algorithm of contour maintaining oriented trajectory doCheckInWindow算法如表2所示,doCheckInWindow算法首先计算射线PaPf的方向,然后计算窗口内每个定位点Pi与PaPf的欧氏距离及方向变化(第5、7行),如果θ或μ被超过,则返回窗口中具有最大欧氏距离误差定位点的索引(第11行)。如果窗口中所有定位点的欧氏距离误差及方向误差均未超过给定阈值,则进一步计算浮动点的前一个点Pf-1的方向变化(第15行),如果Pf-1为拐点,则返回Pf-1的索引(第17行)。如果窗口内没有新的锚点产生,算法返回-1(第19行)。 表2 doCheckInWindow算法Tab.2 doCheckInWindow algorithm 使用Scala语言,选用Geolife数据集作为实验数据。Geolife 数据集由182个用户,历时5年(2007年4月—2012年8月)收集而来。其中73个用户标记了他们轨迹的交通模式,例如:开车、乘公交、骑自行车和步行。Geolife 数据集包含了17 621条轨迹,总长度1 292 951 km,累积时间50 176 h。这些轨迹数据来自不同的GPS 记录器和智能手机,轨迹的采样周期也不尽相同,其中91.5%的轨迹为密集采样,即每隔1~5 s或每隔5~10 m记录一个定位点。 在Geolife数据集中选取了3条不同交通模式的轨迹作为实验数据,轨迹1是一条混合交通模式的轨迹(步行、公交、火车),包含了5 911个定位点,历时229 min。轨迹2为高速公路上汽车行驶的轨迹,其中包含2 167个定位点,历时37 min。轨迹3是一条步行轨迹,其中包含了2 121 个定位点,历时94 min。 为了评估轨迹压缩算法压缩的精确程度,选取了平均欧氏距离误差(average Euclidean distance error,AEDE)及平均方向误差(average heading error,AHE)对算法进行评估。给定原始轨迹T及压缩后的轨迹T′,平均欧氏距离误差及平均方向误差的定义 (5) (6) 由于本文算法通过使用欧氏距离阈值及角度阈值对轨迹的轮廓进行了控制,故该算法的压缩效率受轨迹中定位点方向变化的影响很大。一般来说,用户的行走及移动对象的停留均会造成较大的方向变化。如图4所示,由于轨迹1与轨迹3均包含有步行段,故使用本文算法对轨迹1及轨迹3进行压缩时,压缩率主要受角度阈值的影响。对于轨迹3,设置角度阈值与不设置角度阈值(角度阈值=180°)的压缩率相差较大,因此可以看出轨迹3中定位点的方向变化较大、方向变化频繁。因此在使用其他算法对轨迹3进行压缩时,极易造成轨迹轮廓的丢失。相比于轨迹1与轨迹3,轨迹2为高速公路上汽车的行驶轨迹,因只在服务区和高速公路收费站处停留,其方向变化较小,压缩率同时受距离阈值与角度阈值的影响。 由于轨迹1及轨迹3的方向变化较大,故设置一个相对宽松的角度阈值就能较好地保持其轮廓。而轨迹2由于其本身的方向变化就小,为了较好的保持其轮廓特征,则需要一个相对小的角度阈值。因此,在接下来相同距离阈值的比较中,针对3条轨迹,将算法的角度阈值分别设置为40°、10°及60°。图5为相同距离阈值条件下各算法的平均欧氏距离误差,从图中可以看出本文算法在轨迹1及轨迹3上的误差较小,而在轨迹2上的误差相对较大。 (a) 轨迹1(混合交通模式) (b) 轨迹2(高速公路上汽车的轨迹) (c) 轨迹3(步行轨迹) (a) 轨迹1(混合交通模式)s (b) 轨迹2(高速公路上汽车的轨迹)s (c) 轨迹3(步行轨迹) 平均方向误差在一定程度上可以反映出轨迹轮廓的保持情况,图6为相同距离阈值条件下,平均方向误差的角度对轨迹轮廓的保持情况。从图6中可看出,本文算法具有轮廓保持方面的优势。 由于算法受轨迹方向变化的影响较大,故为了达到指定的压缩率,需要将算法的角度阈值设置为钝角或平角(即不对角度进行控制)。在这种情况下,算法将失去其轮廓保持方面的优势。如图7所示,在相同的压缩率的条件下,在平均欧氏距离误差方面,本文算法及DP算法表现最好。相比于DP算法,本文算法具有支持在线应用的优势。 图8在相同压缩率的条件下,就平均方向误差进行了比较。从图中可以看出,对于轨迹1及轨迹3,本文算法的平均方向误差与DP算法的基本一致,误差较小。对于轨迹2,本文算法的平均方向误差表现居中。 (a) 轨迹1(混合交通模式) (b) 轨迹2(高速公路上汽车的轨迹) (c) 轨迹3(步行轨迹) (a) 轨迹1(混合交通模式) (b) 轨迹2(高速公路上汽车的轨迹) (c) 轨迹3(步行轨迹) (a) 轨迹1(混合交通模式) (b) 轨迹2(高速公路上汽车的轨迹) (c) 轨迹3(步行轨迹) 提出了一种面向轮廓保持的轨迹数据压缩算法,使用欧氏距离阈值和角度阈值,在逐步开放窗口的过程中进行轨迹压缩。通过设置欧氏距离阈值和角度阈值,该算法有效地控制了轨迹的轮廓,确保算法不丢失拐点,解决了轨迹压缩中轮廓丢失的问题。该算法可以在实时接收定位点的过程中进行轨迹压缩,故具有支持在线应用的优势。真实数据集下的实验结果表明,在相同欧氏距离阈值的情况下,本文提出的算法具有轮廓保持方面的优势。在相同压缩率的情况下,也有着不错的表现。 参考文献: [1] 李婷,裴韬,袁烨城.人类活动轨迹的分类、模式和应用研究综述[J].地理科学进展,2014,33(7):938-948. [2] 袁晶.大规模轨迹数据的检索、挖掘和应用[D].合肥:中国科学技术大学,2012. [3] CHEN M J, XU M T, FRANTI P. A fast O(N) multiresolution polygonal approximation algorithm for GPS trajectory simplification[J]. IEEE Transactions on Image Processing, 2012, 21(5): 2770-2785. [4] GIANNOTTI F, NANNI M, PINELLI F, et al. Trajectory pattern mining[C]//ACM, 13th International Conference on Knowledge Discovery and Data Mining. San Jose: ACM, 2007: 330-339. [5] DOUGLAS D H, PEUCKER T K. Algorithms for the reduction of the number of points required to represent a line or its caricature[J]. International Journal for Geographic Information and Geovisualization, 1973, 10(2): 112-122. [6] MERATNIA N, BY R A. Spatiotemporal compression techniques for moving point objects[C]//Springer, 9th International Conference on Extending Database Technology. Crete: Springer, 2004: 765-782. [7] BELLMAN R. On the approximation of curves by line segments using dynamic programming[J]. Communications of the Association for Computing Machinery, 1961, 4(6): 284-286. [8] PEREZ J C, VIDAL E. Optimum polygonal approximation of digitized curves[J]. Pattern Recognition Letters, 1994, 15(8): 743-750. [9] SALOTTI M. Improvement of perez and vidal algorithm for the decomposition of digitized curves into line segments[C]//IEEE, 15th Conference on Pattern Recognition. Barcelona: IEEE, 2000: 2878-2882. [10] SALOTTI M. An efficient algorithm for the optimal polygonal approximation of digitized curves[J]. Pattern Recognition Letters, 2001, 22(2): 215-221. [12] CHEN Y K, JIANG K, ZHENG Y, et al. Trajectory simplification method for location-based social networking services[C]//ACM, 2009 International Workshop on Location Based Social Networks. Seattle: ACM, 2009: 33-40. [13] MUCKELL J, OLSEN P W, HWANG J H, et al. Compression of trajectory data: a comprehensive evaluation and new approach[J]. GeoInformatica, 2014, 18(3): 435-460. [14] MUCKELL J, HWANG J, PATIL V, et al. SQUISH: an online approach for GPS trajectory compression[C]//ACM, 2nd International Conference on Computing for Geospatial Research and Applications. Washington: ACM, 2011:13. [15] ZHENG Y, ZHANG L, XIE X, et al. Mining interesting locations and travel sequences from GPS trajectories[C]//ACM, International Conference on World Wild Web. Madrid: ACM, 2009: 791-800. [16] ZHENG Y, LI Q, CHEN Y K, et al. Understanding mobility based on GPS data[C]//Proceedings of the 10th International Conference on Ubiquitous Computing. Seoul: ACM, 2008: 312-321. [17] ZHENG Y, XIE X, MA W Y. GeoLife: a collaborative social networking service among user, location and trajectory[J]. Bulletin of the Technical Committee on Data Engineering, 2010, 33(2): 32-40.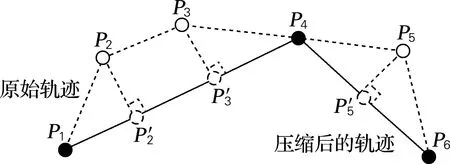
2 面向轮廓保持的轨迹压缩算法
2.1 算法描述
2.2 算法伪代码


3 算法评估
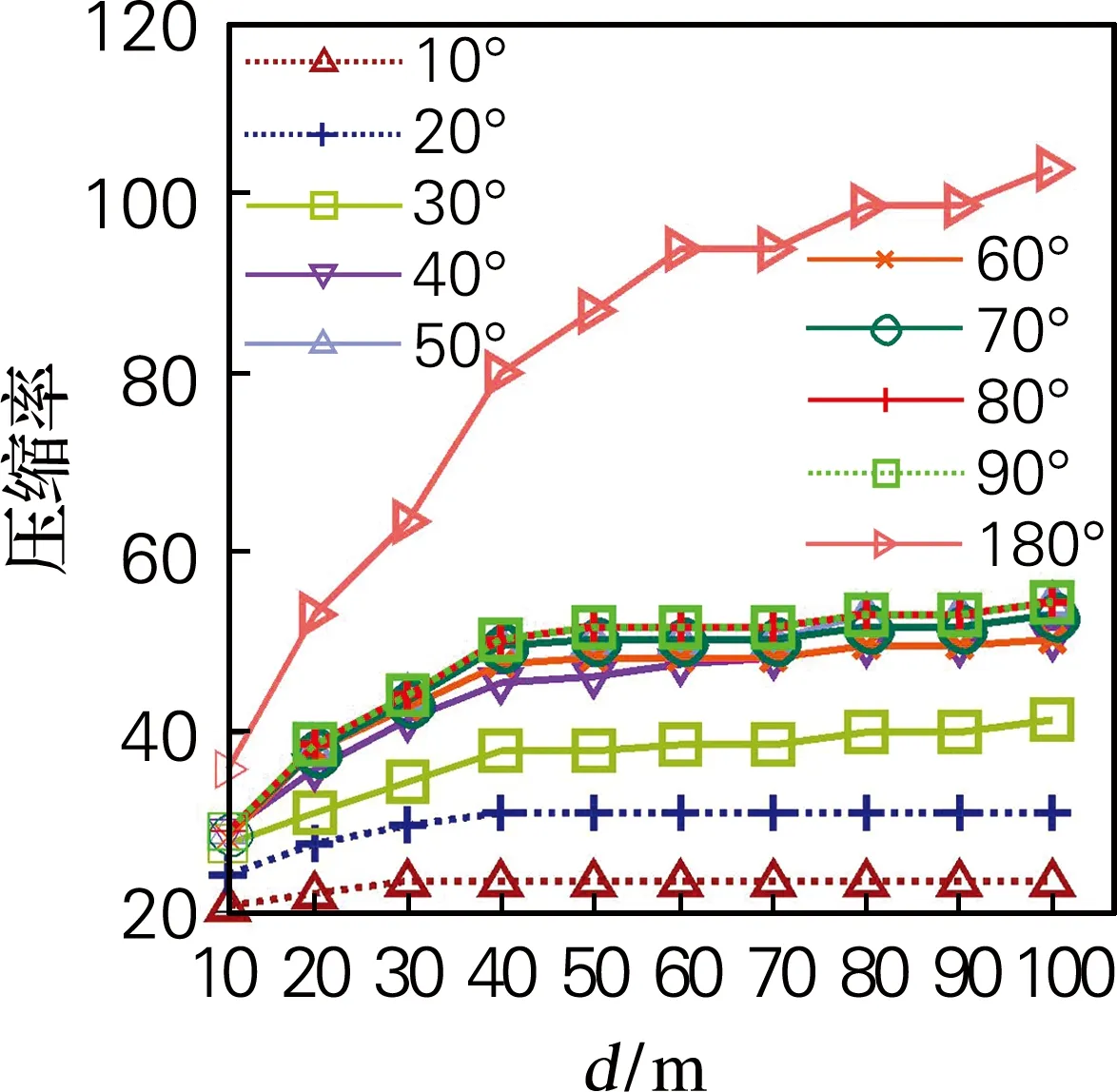
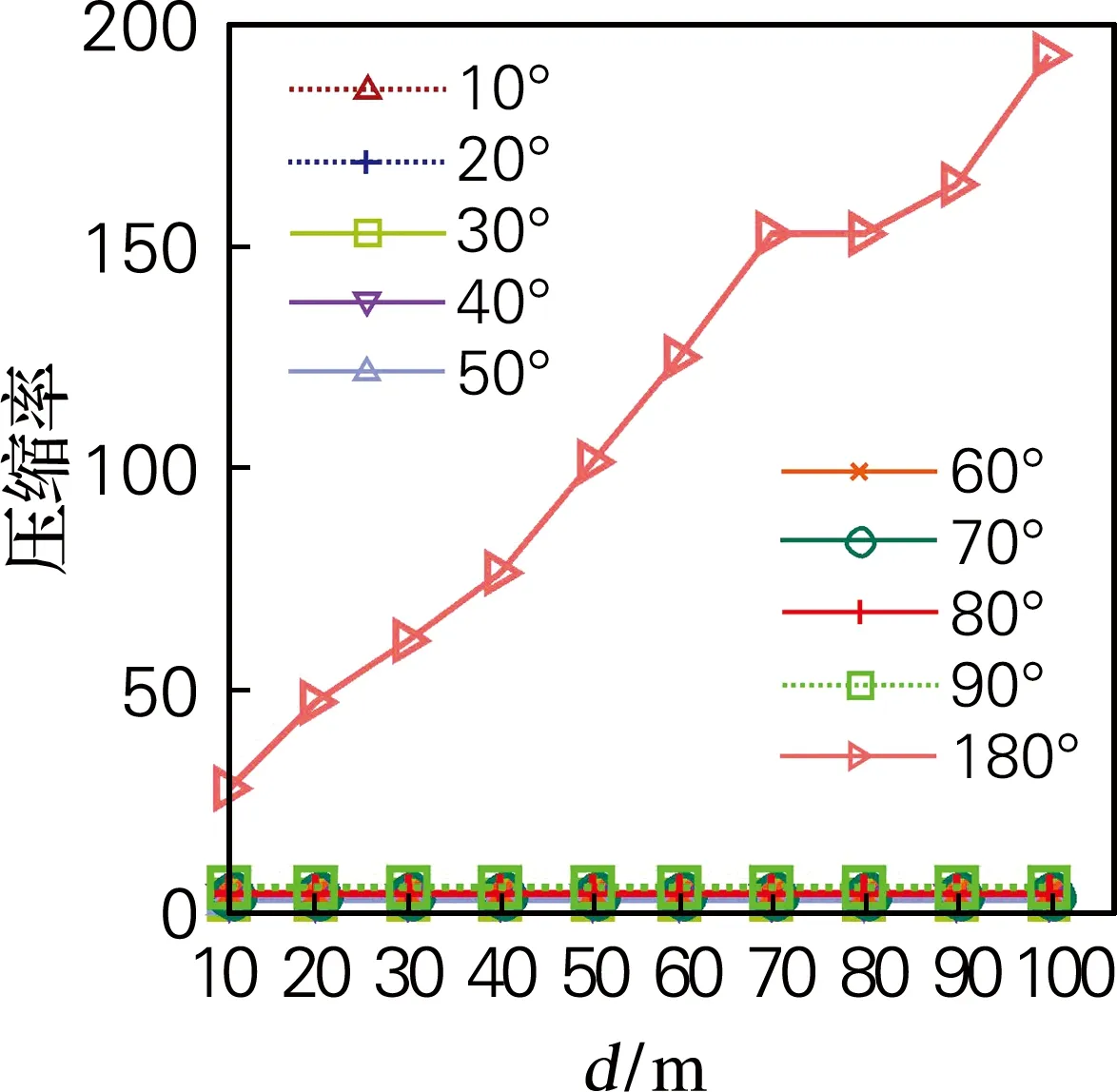
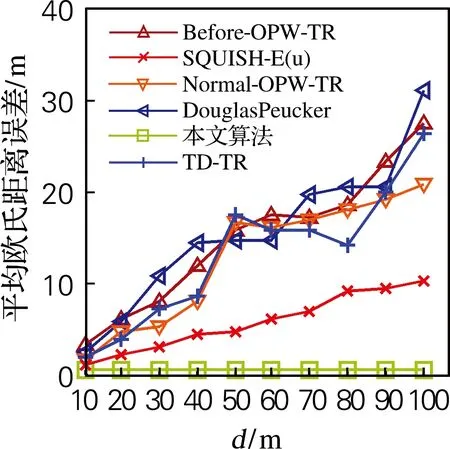
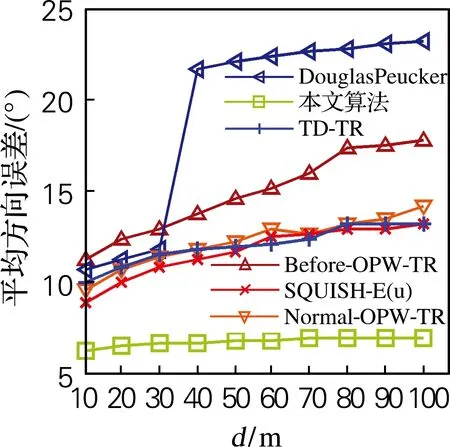
3.1 相同距离阈值下各算法的比较
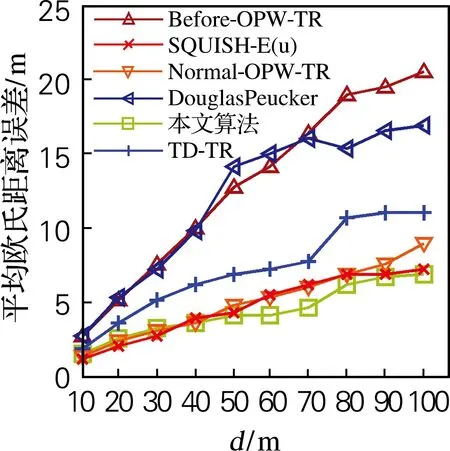
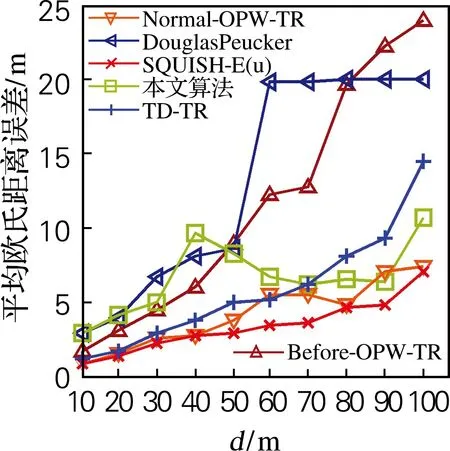
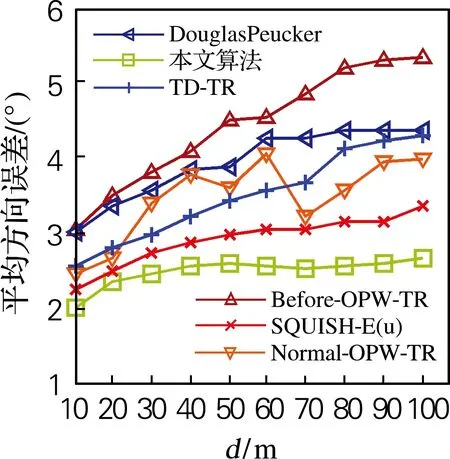
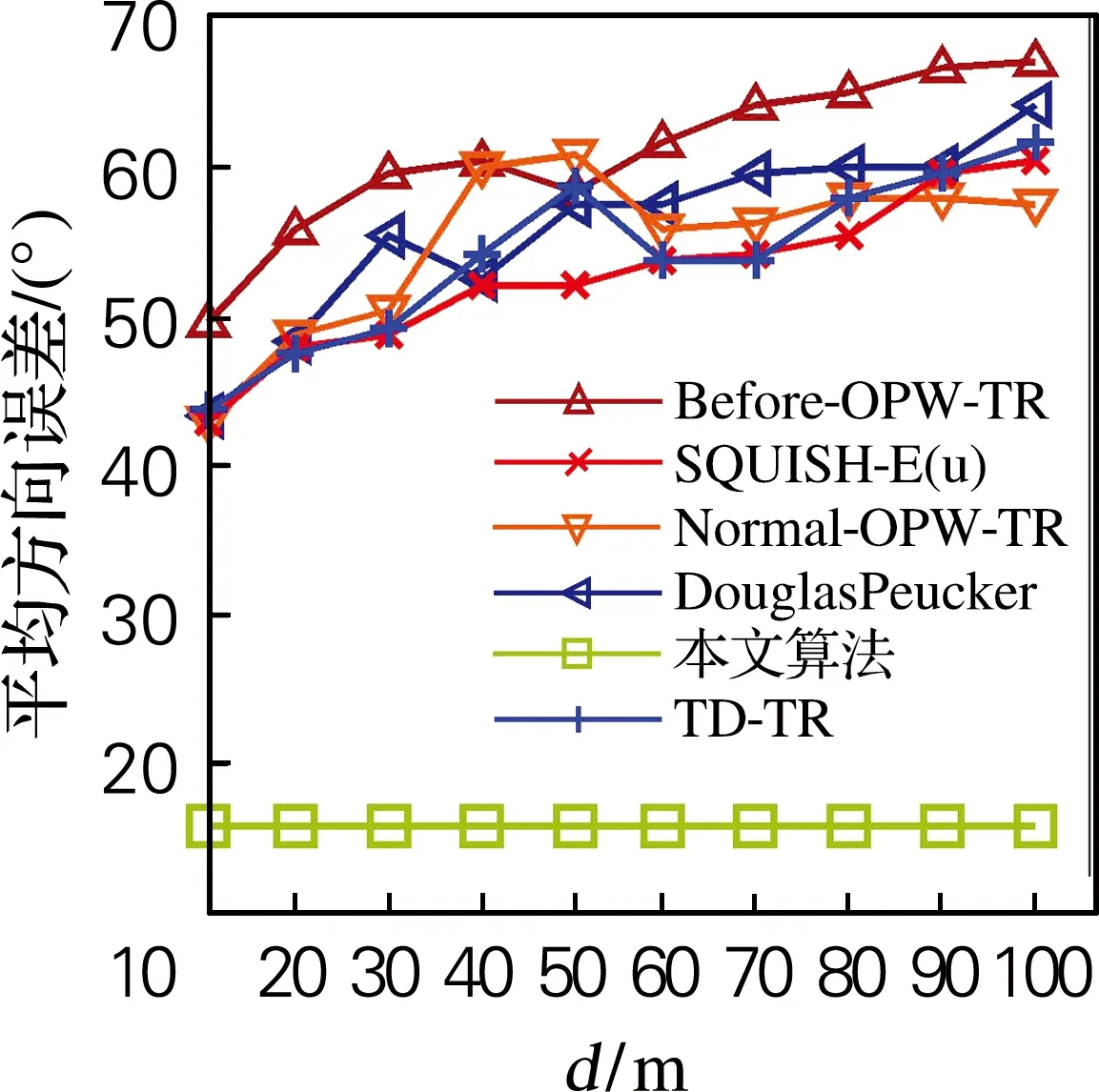
3.2 相同压缩率下各算法的比较

4 结 论

