基于GARCH-MIDAS模型的上证50指数波动率预测

　

(同济大学经济与管理学院　上海　200000)

一、引言

投资者在股票投资活动中，除了关注收益之外，另一个关注重点就是股票波动性，股票市场的动荡程度及未来波动性关乎着投资者的切身利益。股票市场适度的波动有助于实现经济资源的合理配置，而过度的波动则会引起社会动荡。同时，股票市场波动率相关的运用也极为广泛，波动率的预测可以运用在风险管理、资产配置、投资组合和期权定价等领域，市场监管者也需要对未来波动性进行预测，这些领域对不同期限水平的波动率的预测都有着迫切需求。

期权Black-Scholes定价模型中，波动率是重要的变量。目前我国已推出上证50eft期权，对波动率的研究有利于实现期权定价，促进期权市场发展。本文采用广义自回归条件异方差混频数据抽样模型(GARCH-MIDAS模型)对上证50指数波动率进行研究。该模型克服了通过升、降频带来的信息失真的问题，对混频数据进行分析，同时将上证50指数波动率与宏观经济运行情况相关联，对于政府分析宏观经济对股票市场的影响并加强股票市场波动趋势研判，进而制定相应的经济政策，防控股票市场剧烈波动有着重要的借鉴和指导意义。

本文其他部分安排如下：第二部分理论介绍，搭建GARCH-MIDAS模型；第三部分进行实证分析；第四部分为本文结论。

二、理论模型

在实践中，搭建模型时混频数据更为常见，常常需要对不同频度的数据进行分析。对于混频数据常用的方法为加总法或插值法，前者会造成严重的数据信息丢失，后者则会人为的制造信息。针对这两个情况，Ghysels et al(2004)首次引入混频数据抽样(Mixed Data Sampling,MIDAS)模型，突破了传统模型同频数据的约束，直接运用混频数据进行建模，能够有效的运用高频数据信息。Ghysels et al.(2006)首先将MIDAS模型引入到波动率预测中，Clements和Galvão(2006)、Clements et al.(2006)、蔡宇(2015)等人也采用这种方法对波动率进行了研究。

Engle et al(2009)将Spline-GARCH和MIDAD模型相结合形成GARCH-MIDAS模型，将股票市场波动分解为长期成分和短期成分，短期成分采用GARCH模型分析，而长期成分则以通货膨胀率和工业增速来刻画，Engle 和 Rangle(2008)认为对资产收益率的冲击具有时变方差，该时变方差会受到来自某一信息事件对收益率的冲击影响，该次冲击由作用强度和作用乘子决定，该信息事件冲击的作用乘子决定于整体所处宏观经济环境，因此未预期的收益率冲击可以表示为公式1：

(1)

其中，εi,t表示某一信息事件对未预期收益率冲击的作用强度，τt*gi表示该信息事件对未预期收益率冲击的作用乘子。因此，波动率至少由两个成分构成，即计量短期波动的短期成分gi,t和代表长期波动的长期成分τi。公式1的主要思想是基于同一信息的冲击取决于经济体所处的状态，比如收入的下降在繁荣和萧条时期的冲击是不一样的。短期成分gi,t假设与每日的流动性因素、日内交易特征或者其他短期因素相关，gi,t可视为非负的时间序列(本文假定gi,t～GARCH(1,1)过程)。与之相反，长期成分τi主要与未来的现金流、通胀率等宏观经济基本面等因素有关。εi,t为标准化的白噪声过程，即εi,t|ψi-1,t～N(0,1)，ψi-1,t表示在第t时期t-1日可获得的历史信息集合。根据前述假定，gi,t有以下形式：

gi,t=(1-α-β)+(ri-1,t-μ)2/τt+β*gi-1,t

(2)

公式2中的τi表示股票市场波动率中的长期低频成分，可以由某一个低频变量刻画，本文通过宏观经济变量低频因子来描述该成分。具体形式如下：

(3)

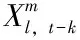
三、实证分析

上证50指数于2004年1月2日正式发布，研究涉及到月底低频数据，为了保障样本的充分性，样本区间为2004年2月2日至2017年10月30日，共计3346日、165月。日度收益率为通过上证50指数每日收盘价原始数据计算得到的对数收益率；月度低频已实现波动率基于日收益率获得，数据来源于wind数据库。

从图3～图5可以看出:(1)ωc越大,谐振带宽越宽,ωc越小,带宽越窄,对基波频率的控制效果越好,一般情况下ωc的取值介于5 rad/s～15 rad/s;(2)KR越大,控制器的峰值增益越大,而谐振带宽几乎没有影响;(3)Kp越大,系统比例增益越大[11]。

其次，宏观经济变量选取代表中国经济运行情况的先行指数和一致指数。先行指数可以揭示出经济的未来变化趋势，一致指数则可以综合反映总体经济的变动情况。相对于GDP和工业增加值指标，两个景气指数具有较高的月度频率，同时能全面反映宏观经济周期状况。本文需要两个指数水平值和波动率，水平值通过与1996年的基数100做差值处理，而波动率序列通过AR(p)模型计算获得。

根据AIC和BIC准则，先行指数水平值、先行指数波动率、一致指数水平和一致指数波动率作为变量的滞后期分别为9、11、18和12个月，在相应的滞后期下，实证结果如表1所示：

表1　基于先行指数和一致指数的GARCH-MIDAS估计结果

注：***、**、和*分别代表1%、5%、10%的显著性水平；表中四列分别代表先行指数和一直指数的水平值和波动率；列名末尾的数字表示滞后期数。

从表中可以看到，各模型参数大都是在不同水平下显著的，从AIC和BIC信息可以看到，基于先行指数拟合优于一致指数，且基于先行指数水平值模型表现表现最佳。四个模型的θ都是显著的正值，表明宏观经济情况对上证50指数波动具有显著地长期影响，且宏观经济剧烈波动将导致上证50指数处于长期高波动水平，这符合相关理论的基本观点与经济直觉。除了基于先行指数水平值的模型，其他三个模型具有比较接近的显著正截距。四个模型的权重参数ω1和ω2都大于1，权重形式呈现先增后减分布，基于水平值的参数值较小，而波动率的参数值较大。先行指数水平值和波动率以及一致指数水平值具有比较接近于1的α+β值，表明三个变量对长期成分的影响具有持续性，且影响以较慢速的度衰减。

本文接下来将采用滚动窗口的样本外预测方法进一步研究宏观因子和已实现波动率模型对传统GARCH(1,1)模型预测精度的改进情况。在本部分中，具体处理包括：首先运用模型计算出一步向前的样本外日度波动率预测值；其次对每月的日预测波动率进行加总处理，构造出月度的波动率；然后利用预测月波动率和月已实现波动率计算损失函数值，衡量模型预测效果；最后，采取GARCH(1,1)作为基准模型，将GARCH -MIDAS模型预测损失函数值与GARCH(1,1)模型预测损失函数值进行比较，判断预测精准度，比较时采取相对分析方法，即将GARCH -MIDAS模型预测损失函数值与GARCH(1,1)模型预测损失函数值相除得到rMSE。本部分设定的样本内区间为2004年2月2日至2015年12月31日，共包含2901日、143个月；样本外预测区间为2016年1月4日至2017年10月31日，共包括含445日、22个月。

表2给出了各模型的rMSE值，可以看出，所有的GARCH-MIDAS模型都能够提高月波动率的预测精度，起到对GARCH模型的改进作用。几个模型中，先行指数水平值具有最小rMSE值，预测精准度最佳，同时一致指数波动率的预测效果最差，先行指数的水平值和波动率预测精准度均优于基于一致指数的预测精准度。与一致指数水平值相比，已实现波动率刻画的长期成分也具有比较好的预测效果，但预测效果又略差于一致指数波动率。

表2　GARCH-MIDAS模型预测效果分析

四、结论

本文主要基于GARCH-MIDAS模型研究了宏观经济运行情况对上证50指数波动率的影响以及运用宏观经济变量对指数波动率进行预测。研究发现，宏观经济景气指数对上证50指数波动率具有显著的影响，而先行指数的影响更为显著，对指数波动率的预测效果也最佳。先行指数反映的是对未来宏观经济运行状况的预期，可以揭示出经济的未来变化趋势，能够影响投资者对未来股价的预期，进而对波动率造成影响。通过比较研究，GARCH-MIDAS模型比传统的GARCH(1,1)模型能够更好的预测上证50指数的波动率。GARCH-MIDAS模型将指数波动率分解成长、短期成分，分别进行分析，将长期成分与宏观经济相关联，能够更好的进行预测。

【参考文献】

[1]Engle R F.Autoregressive Conditional Heteroscedasticity with Estimates of the Variance of United Kingdom Inflation[J].Econometrica,1982,50(4):987-1007.

[3]Ghysels E,Santa-Clara P,Valkanov R.Predicting volatility:getting the most out of return data sampled at different frequencies[J].Journal of Econometrics,2006,131(1-2):59-95.

[4]Ghysels E,Santa-Clara P,Valkanov R.The MIDAS Touch:Mixed Data Sampling Regressions[J].Cirano Working Papers,2004,5(1):512-517.

[5]Ghysels E,Valkanov R.Forecasting Volatility with MIDAS[M].Handbook of Volatility Models and Their Applications.2012:383-401.

[6]蔡宇.产出增长率与通货膨胀率预测研究——基于混频数据取样方法[J].财经问题研究,2015(5):12-19.

[7]史可.基于混频数据的我国股市波动性研究[D].南京财经大学,2014.

[8]唐小峰.基于GARCH模型族的沪市波动性实证分析[D].华东师范大学,2008.

[9]王建,何娟.考虑外部系统性风险因素的供应链金融长期价格风险测度研究[J].金融经济学研究,2016,31(04):47-59.

[10]王晓辉.金融市场波动率模型的参数估计及预测研究[D].华南理工大学,2015.

[11]王艳歌.宏观经济与股票市场波动内在关联性研究[D].武汉大学,2017.

[12]王永莲.我国股票市场波动与经济政策不确定性的关联性研究[D].吉林大学,2017.

[13]徐剑刚,张晓蓉,唐国兴.混合数据抽样波动模型[J].数量经济技术经济研究,2007,24(11):77-85.

[14]郑挺国,尚玉皇.基于宏观基本面的股市波动度量与预测[J].世界经济,2014(12):118-139.