Modeling TCP Incast Issue in Data Center Networks and an Adaptive Application-Layer Solution

Jin-Tang Luo, Jie Xu, and Jian Sun

1.Introduction

In data centers, an application often simultaneously requests data from numerous servers. This results in a many-to-one traffic pattern where multiple servers concurrently send data fragments to a single client via a bottleneck switch. For instance, in web search, a search query is partitioned and assigned to many workers, and then the workers’ responses are aggregated to generate the final result. As the number of concurrent senders increases, the bottleneck switch buffer which is usually shallow[1]can be easily overflowed, leading to massive packet losses and subsequent transmission control protocol （TCP） timeouts. As the minimum retransmission timeout (minRTO) is much greater than the round-trip delay in data centers, even one timeout remarkably prolongs the overall data transmission time. Hence, the client’s goodput decreases to be lower than the link capacity by one or even two orders of magnitude. Such catastrophic TCP goodput collapse for applications with many-to-one traffic pattern is referred to as TCP incast[1].

Many solutions to the TCP incast issue have been proposed from the aspects of different layers. For instance, at the Ethernet layer, the fully-qualified class name (FQCN)[2]uses explicit network feedback to control congestion among switches;at Internet protocol (IP) layer, [3] explores the effectiveness of tuning explicit congestion notification (ECN) to mitigate incast,and the cyclic prefix (CP)[4]drops only the packet payload instead of the entire packet upon congestion to reduce timeout possibility; at the transport layer, data center TCP (DCTCP)[5],predicted rice interactome network (PRIN)[6], and pFabric[7]decrease the timeout possibility through the cooperation of end-hosts and network; by adding a “shim layer” to the data receiver, incast congestion control for TCP (ICTCP)[8], proxy auto config (PAC)[9]and deadline and incast aware TCP(DIATCP)[10]proactively adjust the in-flight data size to reduce the packet loss; and at the application layer, [1] and [11]-[13]restrict the number of concurrent connections to avert incast.Among these proposals, the application-layer solutions are most practical for their low deployment barrier and minimal impact on ordinary one-to-one applications. Indeed, Ethernetlayer solutions require hardware revisions not supported by current commodity switches, and transport-layer and shimlayer solutions may cause fairness issues to ordinary applications running on regular TCP. In contrary, application-layer solutions merely regulate the data transfer of applications with the manyto-one traffic pattern, so they are easy to deploy and pose no side effect on ordinary applications.

Despite of the numerous application-layer solutions in literature, few works analytically study how application’s regulation on data transfer can affect incast. Currently, there are several analytical models for the TCP incast problem[1],[6],[11],[14]. However, most of them either ignore the possible existence of background TCP traffic[1],[11], or oversimplify the application layer as a dumb data source/sink without the ability to control data transfers[6],[14]. Therefore, the existing models provide few useful insights into addressing incast from the application layer, which explains why the current application-layer solutions can only avert incast in known and predefined network environments, e.g., the bottleneck link is the last-hop link to the receiver[12],[13], or the available bottleneck bandwidth is known by the receiver[1],[11]).But in real data centers, many network parameters may change drastically and cannot be known in prior. For instance, the bottleneck link often varies due to load balancing, and available bandwidth may fluctuate drastically in the presence of background TCP traffic. In these varying environments, the current solutions often fail to effectively prevent TCP incast, as demonstrated in Section 4.

In this paper, we intend to understand and solve the TCP incast problem from the viewpoint of applications. Toward this goal, we first develop an analytical model to comprehensively investigate the impact of the application layer on incast.Then under the model’s enlightenment, we propose an adaptive application-layer control mechanism to eliminate incast.

Since incast is essentially caused by TCP timeout, here we focus on modeling the relationship between the appearance of timeout and various factors related to applications, including the network environment and connection variables. Compared with the existing models[1],[6],[11],[14], our model is based on more general assumptions about TCP behaviors, and it considers the impact of background TCP connections on incurring timeout.In addition, integrated with the optimization theory, the model provides some insightful guidelines for dynamically tuning connection variables to minimize the incast probability in a wide range of network environments.

According to the theoretical results, the crux of avoiding timeout is to adaptively adjust the number of concurrent connections and equally allocate the sending rate to connections. Following this idea, we design an applicationlayer incast probability minimization mechanism (AIPM),which only modifies receiver-side applications to avert timeout. With AIPM, a client (receiver) concurrently sets up a small number of connections, and assigns an equal TCP advertised window (awnd) to each connection. After a connection finishes data transferring, a new connection can be started. The regulation of awnd is based on network settings and the amount of concurrent connections. The concurrency amount is decided by a sliding connectionwindow mechanism similar to TCP’s congestion control. By this mechanism, the connection-window size grows gradually upon a successful data transmission and shrinks as a connection is “lost”. A connection is considered as the lost connection when three new connections have finished since the last time it transmits new data. The lost connection is terminated at once and will be re-established when allowed by the connection-window.

The simulations show that AIPM effectively eludes incast and consistently achieves high performance in various scenarios. Particularly, in a leaf-spine-topology network with dynamic background TCP traffic, AIPM’s goodput is above 68% of the bottleneck capacity, while the proposals in [1]and [11] both suffer from rather low goodput (＜ 30%) due to incast.

The major contributions of this paper are two-folds:

● Build an analytical model to disclose the influence of network environment and connection variables on the occurrence of incast. The model provides some insightful guidelines for tuning connection variables to minimize incast possibility.

● Design an adaptive application-layer solution to the TCP incast problem. To our best knowledge, this solution is the first application-layer solution that can efficiently control incast in network environments with dynamic background TCP traffic and multiple bottleneck links.

The rest of the paper is organized as follows. Section 2 describes our model for incast probability and provides some insightful guidelines for taming incast. Section 3 proposes an adaptive application-layer solution to incast, namely, AIPM. In Section 4 we evaluate AIPM in various scenarios using NS2 simulations. Section 5 concludes the paper.

2.Modeling and Minimizing TCP Incast Probability

As a data requestor, the receiver-side application (i.e., the client) can implicitly manage data transmission by adjusting connection variables (including the number of concurrent connections and the sending window size for each connection).This fact enlightens us to model the TCP incast probability as a function of connection variables. Based on this model, we derive the conditions on which the incast risk is minimal.

2.1　Notations and Assumptions

First of all, we put forward an important concept related to data transfers of concurrently living connections, called round.The first round starts from the beginning of data transmission from an endpoint, and lasts one round-trip time (RTT). The next round starts from the end of last round and lasts one RTT.

Then consider the TCP incast scenario in Fig. 1. Let R be the number of rounds for transmitting data. During the kth round, there are n(k) servers sending data fragments, formally termed as a sever request unit (SRU) to a client via a common bottleneck link. The ith server’s sending rate is xi(k), and its sending window is wi(k), for 1≤i≤n. The bottleneck link is also shared by m(k) background connections from other applications,whose sending rates are yj(k) for. For the bottleneck link, its capacity is C packets per second, its buffer size is B packets, and the propagation RTT is D. The rest notations are summarized in Table 1.

We also make some assumptions to facilitate modeling.Firstly, we assume that the queuing policy of the bottleneck link is drop-tail. Secondly, we assume the spare bottleneck buffer is ignorable compared with the sum of the sending windows. This assumption is reasonable due to the “buffer pressure” phenomenon and the fact that switches’ buffers are usually very shallow in data centers[1]. Thirdly, we assume that a connection sees timeout only if the entire window of packets are lost. Most researches[5],[14]have shown that the full-window loss is the dominating kind of timeout that causes TCP incast, thus other kinds of timeout are trivial while modeling incast. At last, we assume that minRTO =200 ms by default, which is significant for the overall transmission time of the requested data block, so even one timeout leads to TCP incast with drastic goodput degradation.

Fig. 1. General scenario of TCP incast, where multiple servers concurrently transmit data fragraments (SRU) to a single client.

Table 1: Meanings of the commonly used parameters

2.2　Probability of TCP Incast

Now we begin to model the probability of TCP incast as a function of current network condition (i.e., B, C, D, and yi(k))and connection context variables (i.e., n(k) and xi(k)).

First, recall that the client will suffer from incast if it has at least one timeout during R rounds, so the incast probability can be expressed by

where Pi(k) is the timeout probability of the ith connection in the kth round.

The timeout possibility Pi(k) of a connection is determined jointly by the sending window wi(k) and the packet loss rate pi(k) of that connection. Specifically, we consider full window loss as the only cause to timeout, thus Pi(k) equals to

The next task is to derive the packet drop rate pi(k). As we assumed previously, the spare bottleneck buffer is ignorable compared with the sum of the servers’ sending windows,which means that the bottleneck link would drop packets once the servers start transmitting data. We denoteas the sum of the servers’ sending rates,andas the sum of the background connections’ sending rates. During the kth round, packets are injected into the network at the total rate of, and are processed by the bottleneck link at the rate of C.Henceforth, the drop rate pi(k) is

Moreover, a connection’s sending window wi(k) is related with its sending rate xi(k) and RTT D as

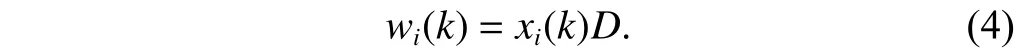
Eventually, by substituting (2) to (4) into (1), we derive the TCP incast probability as an analytical function of network condition (i.e., B, C, D, and Y(k)) and connection variables (i.e.,n(k) and xi(k)) as follows:

2.3　Minimizing Incast Probability

As (5) indicates, to minimize the incast probability Pincast,we must minimize the timeout probability in every round. This is to maximize the timeout-free possibility that no connection ever incurs timeout in any round k as follows

Here we explore how could the client maximize the timeout-free probability (6) through adjusting the sending ratesand the connection amount n(k).To reveal the individual impact of a parameter on timeout, we analyze it by keeping other parameters unchanged. Because our analysis below focuses on maximizing (6) in every single round, we simply omit the round number k in the notations, like n(k) to n.

1) Adjusting sending sizes, x: We fix other parameters. Then the maximization of the timeout-free probability in (6) is to solve the optimization problem below:

It is straightforward to check that the Hessian matrix of−ln[f(x)] is positive semi-definite over the region x≥0, which means that ln[f(x)] is a concave function. This gives our analysis a great convenience. Specifically, the method of the Lagrange multiplier states that ln[f(x)] is globally maximized by the sending rate allocationif and only if

The unique solution of (8) that maximizes ln[f(x)] is

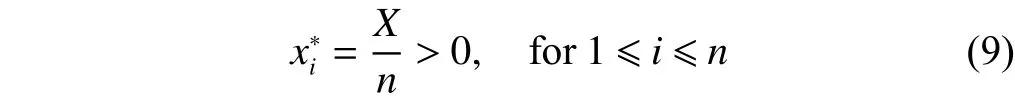
which also minimizes the incast probability (6).

Remark 1: To minimize the incast risk, the connections should always be given a same sending rate. This operation is feasible at the client application, as the client knows the concurrent connections’ number n, and it is able to implicitly control each connection’s sending rate xithrough modifying the TCP advertised window field in acknowledgement (ACK)packets.

Remark 2: While the sending rates’ sum X is assumed as a constant for deriving (9), actually the client can change X by tuning the sending rates. But as proved in Appendix,the optimal X that can minimize the incast probability is dependent on the background traffic Y. Since the client does not know Y, it is unable to properly set X to prevent incast.

2) Adjusting the concurrent connections’ number, n: We fix other parameters. According to (6) and (9),we optimally set the sending rates to be xi=X/n for 1≤i≤n and rewrite the timeout-free probability as

which is always negative since p lies in (0, 1). This suggests that the timeout-free probability (10) decreases with the concurrent connection number n. Henceforth, the incast probability is an increasing function of n and will be minimized at n=1.

Remark: The client should lower the number of concurrent connections n to reduce the incast risk. On the other hand, an excessively small n may cause a great waste of bandwidth in the cases where each connection has so little data to send SRU that it finishes sending before fully utilizing the bandwidth.How to properly set n will be discussed in the next section.

3.Minimizing Incast Probability at Application Layer

Based on the analyses of (9) and (11), we propose an AIPM scheme. The AIPM is implemented at the client application, and it minimizes the incast probability via equally allocating advertised windows of concurrent connections and dynamically adjusting concurrent connections’ amount.

3.1　Allocate Equal Advertised Window to Connections

As (9) indicates, the risk of TCP incast is minimal if the existing connections have an equal sending rate. However,AIPM is essentially a part of the client application, which means it cannot directly control each connection’s sending rate. Therefore, AIPM emulates the equal sending rate allocation by setting awnd at the client (e.g., via calling the setsokopt() application programming interface (API) in Berkeley software distribution (BSD) systems) as follows.

First, according to (4) and (9), the ideal sending rate allocation is equivalent to the following sending window allocation:

where X is the total sending rate of AIPM’s n connections,and D is RTT without queuing.

Next, AIPM should let X equal the bottleneck capacity C,so that it can fully utilize the bottleneck link without selfinduced drops. From X=C and (12), we derive that

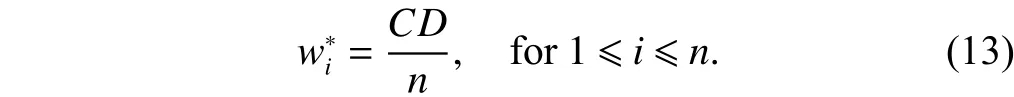
Finally, since TCP’s sending window size is upperbounded by the advertised window size (awnd), AIPM can emulate the equal sending window assignment in (13) by assigning an identical awnd to its connections as

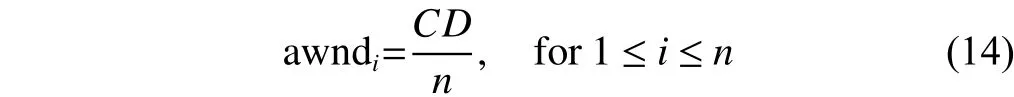
where awndiis awnd of the connection i. Although such emulation is suboptimal, it avoids the polarized allocation of sending window sizes and thus decreases the timeout probability.

Naturally, even if AIPM strictly follows (14) and equally allocates awnd to its connections, timeout may still happen due to the background traffic. Therefore, AIPM must further decrease timeout risk by adaptively tuning the connections’ amount. Besides, it must quickly recover data transmission from the timeout connections. These two demands can be met by the following two mechanisms,respectively.

3.2　Determine the Proper Number of Concurrent Connections with Sliding Window Mechanism

To reduce the timeout probability while keeping high goodput, AIPM must selectively connect to a subset of the servers at one time. The question is which servers AIPM should connect to. To find the answer, AIPM employs a sliding-window-like mechanism to maintain a window of the concurrently existing connections. In concept, we term this window as the connection window, or shortly, con_wnd. When the existing connections are less than the con_wnd size, AIPM establishes a new connection and admits it to con_wnd. When a connection finishes, AIPM removes it from con_wnd.

AIPM uses an additive increase multiplicative decrease(AIMD) policy to decide the con_wnd size n. The initial value for n is n=1. Whenever a connection in con_wnd completes,AIPM infers that the bottleneck link is not jamming, thus it gradually increases n as

The growth of the concurrent connections inevitably leads to timeout. Based on the fact that minRTO=200 ms, is much greater than a connection’s ordinary life period(mostly less than 1 ms). The AIPM deduces a connection to be timeout if three new connections have been admitted and finished since the last time the connection transmitted any data.

After detecting timeout, AIPM realizes that the timeout probability right now is too high. According to (11), AIPM can reduce the timeout probability by lowering the number of concurrent connections n while fixing other parameters. Hence,AIPM halves con_wnd as follows:

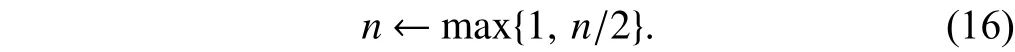
Because AIPM does not reduce the total awnd when performing (16), the live connections that are not timeout can quickly occupy the spare bandwidth and maintain relatively high link utilization.

3.3　Fast Reconnection and Slow Withdrawal

1) Fast reconnection: For a timeout-broken data connection, AIPM terminates that connection (by sending finish (FIN) to the connection’s server) and removes it from con_wnd. Then AIPM will reconnect to the data server as long as con_wnd allows. Since the SRU is so small(typically dozens of KB), the server can retransmit it within an ignorable period of time. This scheme is termed as fast reconnection. It enables AIPM to quickly recover data transmission from the timeout-broken servers rather than being slowed down by TCP’s sluggish timeout retransmission mechanism.

2) Slow withdrawal: As timeout occurs to some connections,if AIPM naively follows (16) and instantly halves the number of the concurrent connections, it may have to close some live connections that are not timeout. Nevertheless, these live connections have already cut their sending windows after seeing packet losses and are unlikely to cause more timeout situation. Therefore, closing these live connections at one time will result in unnecessary data retransmissions and may even lead to link under-utilization.

To solve the above two issues, AIPM adopts the slow withdrawal scheme in the presence of timeout. Specifically,upon detecting timeout, AIPM records the current con_wnd size n, and then slowly decreases con_wnd by one after each live connection finishes. This means that AIPM does not close any live connections that are still transmitting data. Moreover,this gives the live connections sufficient time to grow their congestion windows and to fully utilize the spare bandwidth left by the closed or timeout connections (since the delays in datacenters are so small, the live connections can grow their congestion windows very fast). Once con_wnd shrinks to n/2,AIPM ends slow withdrawal and resumes to the normal AI operation (15).

3.4　Some Discussions about Design Issues

1) How can AIPM know the bottleneck link’s capacity,C? Nowadays datacenters employ several mechanisms like offering the uniform high capacity between racks and load balancing technologies so that congestion only happens at the edge top-of-rack (TOR) switches[8]. This feature allows AIPM to conveniently set C to be the link capacity of TOR switch.

2) How can AIPM know the round-trip propagation delay D? Data center’s network settings (i.e., hardware, framework,topology, etc.) are usually stable over a relatively long period.Thereby, the network administrator can measure D offline and feed the value to AIPM every time network settings change.

3) How should AIPM react if it observes several timeout connections at one time? To avoid the link under- utilization,after detecting timeout-broken connections, AIPM starts slow withdrawal normally and halves the window only once. AIPM will not further halve con_wnd even if it detects more timeoutbroken connections during the slow withdrawal state.

4.Empirical Validations of AIPM

4.1　Simulation Settings

We evaluate the performance of AIPM with NS2 simulation in two different network scenarios. The first one is a single 1 Gbps bottleneck link with a 64 KB buffer and 100 μs RTT. This scenario represents static network environments.The second scenario has the leaf-spine topology as in Fig. 2,which is commonly used in data centers[7]. The network has 144 end-hosts through 9 leaf (i.e., top-of-rack) switches that are connected to 4 spine switches in a full mesh. Each leaf switch has 16 downlinks of 1 Gbps to the hosts and four uplinks of 4 Gbps to the spine. RTT between two hosts connected to different leaf switches is 100 μs. Background TCP flows arrive following the Poisson process, where the source and the destination for each flow are chosen randomly, and each flow’s size satisfies the distribution observed in real-world data mining workloads[7]as shown in Fig. 3. The background flow arrival rate is set to obtain a data load of 0.5. This scenario represents realistic datacenter network environments that are complex and dynamic. Throughout our simulations, the client requests for a data block that is scattered over N servers, and it requests for the next data block after all N servers finish sending the current one. The data packet size is 1000 Byte, and the acknowledgement (ACK) size is 40 Byte.

Fig. 2. Leaf-spine network topology used in the second simulation scenario.

Fig. 3. Flow size distribution in the second simulation scenario is based on real-world measurements of data mining workloads[7].

We compare AIPM with the Naïve method (i.e., the client concurrently connects to all N servers), as well as two state-of-art application-layer solutions, namely, Oracle security developer tools (OSDT)[1]and OSM[11]. Similar to AIPM, these two solutions also try to mitigate incast by restricting the concurrent TCP connections’ number and sending rates. The major difference is that AIPM can correspondingly tune its own parameters for various network scenarios, whereas OSDT and OSM are only specified for predefined environments with single bottleneck link and no background TCP traffic.Due to this difference, AIPM is able to remarkably outperform OSDT and OSM in changing network environments, as we will see below.

4.2　Fixed SRU Size

In this subsection, we fix the SRU size of each server to 256 kB, and investigate the goodput of AIPM in the two aforementioned network scenarios, respectively.

Fig. 4 shows that our solution AIPM achieves best goodput (0.68 Gbps to 0.88 Gbps) in both cases. The reason is that AIPM dynamically adjusts each connection’s advertised window size (awnd) and the connection window size (con_wnd) based on its estimation for the network state(i.e., if some connections incur timeout). Such adjustment enables AIPM to adaptively minimize incast risk and rapidly recover from timeout even in the network environment with multiple bottleneck links and varying background traffic(Fig. 4 (b)).

Reversely, OSDT and OSM both restrict the concurrent connection number by predefined values. Although such fixed values are well suited for static conditions, they can hardly elude incast in dynamic network environments where both bottleneck links and available bandwidth can change drastically. This is why OSDT and OSM only have the goodput less than 0.3 Gbps in Fig. 4 (b).

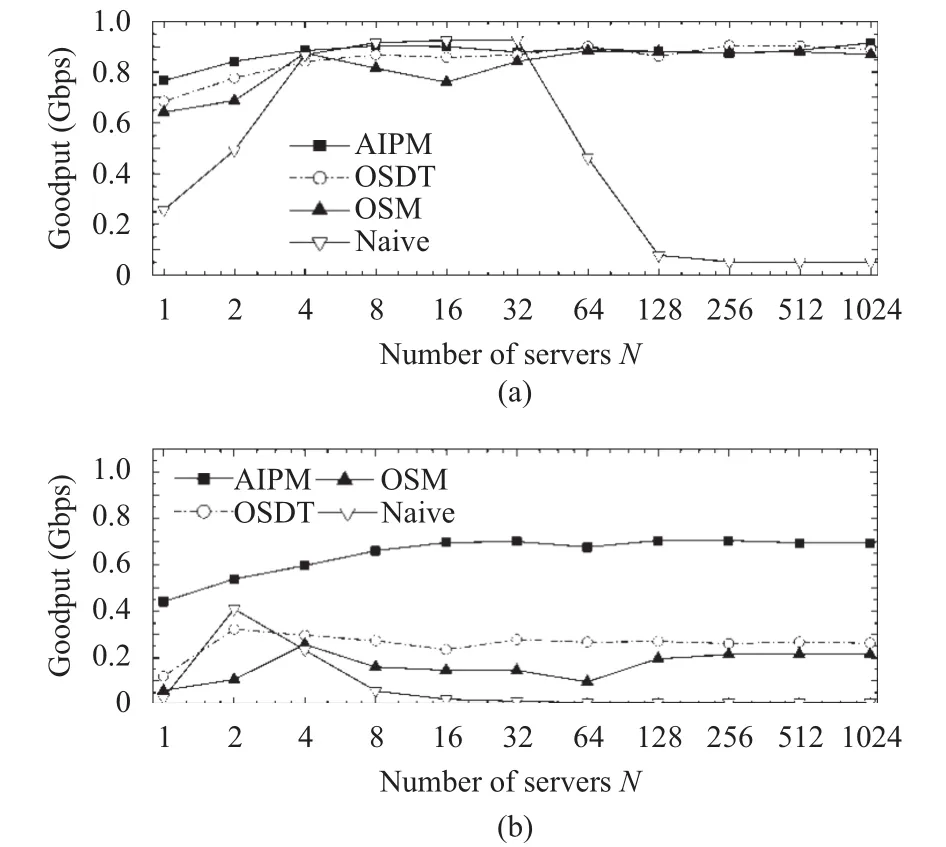
Fig. 4. Goodput with SRU=256 kB for (a) a single bottleneck link without background traffic and (b) leaf-spine topology with background TCP load of 0.5.

4.3　Varying SRU Size

Next, we fix the overall data block size to 2 MB, and set the SRU size to 2 MB/N, where N is the total number of the servers. We evaluate AIPM’s performance in terms of goodput and request completion time.

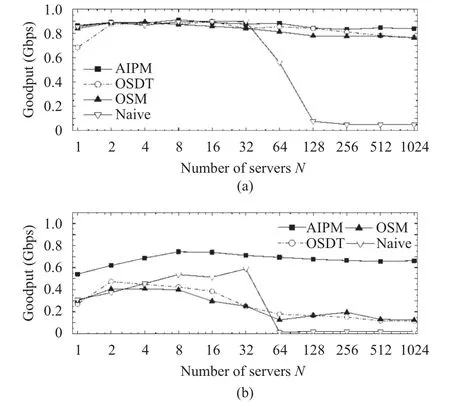
Fig. 5. Goodput with block size=2 MB for (a) a single bottleneck without background traffic and (b) leaf-spine topology with background TCP load of 0.5.

As Fig. 5 illustrates, AIPM achieves higher goodput than the alternative solutions in both network scenarios, which demonstrates again that AIPM can effectively address incast issue even in highly dynamic environments. Observe that AIPM, OSDT, and OSM all have descendant goodput as N grows, for a larger N reduces each server’s SRU and then decreases the average sending window size of the concurrent connections. However, AIPM’s goodput decreases more slowly than the other two’s due to its adaptive adjustment of the number of concurrent connections. Indeed, AIPM adapts to small SRU values by allowing more connections to concurrently send data (i.e., larger con_wnd), so that it can fully utilize the bottleneck link and keep high goodput regardless of the SRU value.

Fig. 6 compares AIPM’s request completion time (RCT)with the other three schemes. As we can see, AIPM’s RCT keeps being the smallest in both scenarios. Particularly, in the leaf-spine scenario, AIPM’s RCT is less than 20% of OSM or OSDT’s RCT, and is less than 3% of Naïve’s RCT.This result clearly demonstrates that AIPM effectively avoids incast by triggering no TCP retransmission timeout.With such small RCT, AIPM makes the client application respond more promptly to the upper-level user, and hence improves user experience.

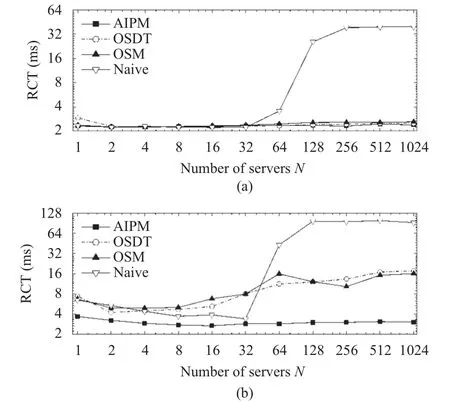
Fig. 6. Request completion time (RCT) with block size=2 MB for(a) a single bottleneck without background traffic and (b) leafspine topology with background TCP load of 0.5.

4.4　Higher Bottleneck Capacity

At last, we explore the scalability of AIPM in higher- speed data centers. In the single-bottleneck scenario, we increase the bottleneck capacity from 1 Gbps to 10 Gbps. In the leaf-spine scenario, we increase the edge link capacity from 1 Gbps to 10 Gbps and the core link capacity from 4 Gbps to 40 Gbps. Other settings remain unchanged, i.e., SRU=256 kB, buffer size=64 kB, and RTT=100 μs.

As we can see in Fig. 7, the goodput of AIPM is generally higher than the goodput of other methods. In particular, AIPM maintains goodput up to 91% of the bottleneck capacity in the network with no background TCP (Fig. 7 (a)), and it achieves nearly two times higher goodput than the alternative solutions while coexisting with the background TCP traffic (Fig. 7 (b)).Such good performance shows that AIPM is readily scalable for higher-speed data centers in future.

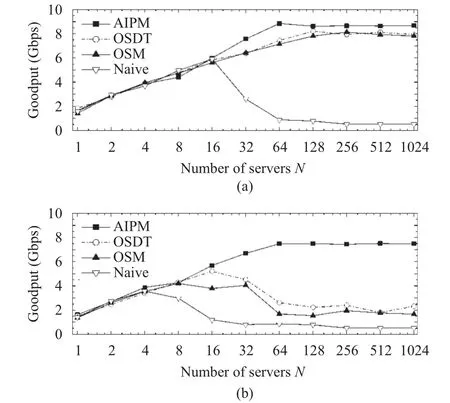
Fig. 7. Goodput with the bottleneck capacity C=10 Gbps for (a) a single bottleneck link without background traffic and (b) leaf-spine topology with background TCP load of 0.5.

5.Conclusions

We built an analytical model to reveal how TCP incast is affected by various factors related to applications. From this model, we derive two guidelines for minimizing the incast risk,including equally allocating the sending rate to connections and restricting the number of concurrent connections.

Based on the analytical results, we designed an adaptive application-layer solution to incast, which allocates an equal advertised window to connections, and uses a slidingconnection-window mechanism to manage concurrent connections. Simulation results indicate that our solution effectively eliminates incast and achieves high goodput in various network scenarios.

Appendix

We adjust the sending rate sum X to maximize the timeoutfree probability in (6) while fixing other parametersAccording to (9), we let the sending rates xibe xi=X/n for 1≤i≤n, and express the timeout-free probability(6) as

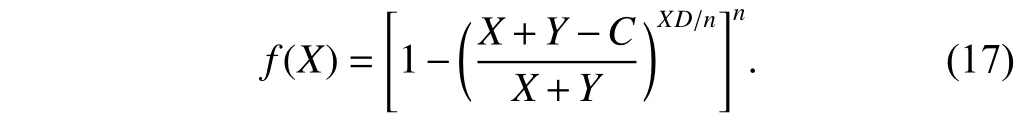
If the background traffic Y is much smaller than the sum of the connections’ sending rates X, the timeout-free probabilityreduces to, which is a decreasing function of X. Reversely, if Y is much greater than X, thenbecomes, which is an increasing function of X. As a result, the optimal X that maximizesis dependent on the background traffic Y.

[1]S. Zhang, Y. Zhang, Y. Qin, Y. Han, Z. Zhao, and S. Ci,“OSDT: A scalable application-level scheduling scheme for TCP incast problem,” inProc. of IEEE Intl. Conf. on Communications, 2015, pp. 325-331.

[2]Y. Zhang and N. Ansari, “On mitigating TCP incast in data center networks,” inProc. of IEEE Conf. on Computer Communications, 2011, pp. 51-55.

[3]H. Wu, J. Ju, G. Lu, C. Guo, Y. Xiong, and Y. Zhang,“Tuning ECN for data center networks,” inProc. of the 8th ACM Intl. Conf. on Emerging Networking Experiments and Technologies, 2012, pp. 25-36.

[4]P. Cheng, F. Ren, R. Shu, and C. Lin, “Catch the whole lot in an action: rapid precise packet loss notification in data centers,” inProc. of the 11th USENIX Symposium on Networked Systems Design and Implementation, 2014, pp.17-28.

[5]M. Alizadeh, A. Greenberg, D. A. Maltz,et al., “Data center TCP,”ACM SIGCOMM Computer Communication Review,vol. 40, no. 4, pp. 63-74, Oct. 2011.

[6]J. Zhang, F. Ren, L. Tang, and C. Lin, “Modeling and solving TCP incast problem in data center networks,”IEEE Trans. on Parallel and Distributed Systems, vol. 26, no. 2,pp. 478-491, Feb. 2015.

[7]M. Alizadeh, S. Yang, M. Sharif,et al., “pFabric: Minimal near-optimal datacenter transport,”ACMSIGCOMM Computer Communication Review, vol. 43, no. 4, pp. 435-446, 2013.

[8]H. Wu, Z. Feng, C. Guo, and Y. Zhang, “ICTCP: Incast congestion control for TCP in data-center networks,”IEEE/ACM Trans. on Networking, vol. 21, no. 2, pp. 345-358, 2013.

[9]W. Bai, K. Chen, H. Wu, W. Lan, and Y. Zhao, “PAC:taming TCP incast congestion using proactive ACK control,”inProc. of IEEE the 22nd Intl. Conf. on Network Protocols,2014, pp. 385-396.

[10]J. Hwang, J. Yoo, and N. Choi, “Deadline and incast aware tcp for cloud data center networks,”Computer Networks, vol.68, pp. 20-34, Feb. 2014.

[11]K. Kajita, S. Osada, Y. Fukushima, and T. Yokohira,“Improvement of a TCP incast avoidance method for data center networks,” inProc. of IEEE Intl. Conf. on ICT Convergence, 2013, pp. 459-464.

[12]H. Zheng and C. Qiao, “An effective approach to preventing TCP incast throughput collapse for data center networks,” inProc. of IEEE Global Telecommunications Conf., 2011, pp.1-6.

[13]Y. Yang, H. Abe, K. Baba, and S. Shimojo, “A scalable approach to avoid incast problem from application layer,” inProc. of IEEE the 37th Annual Computer Software and Applications Conf. Workshops, 2013, pp. 713-718.

[14]W. Chen, F. Ren, J. Xie, C. Lin, K. Yin, and F. Baker,“Comprehensive understanding of TCP incast problem,” inProc. of IEEE Conf. on Computer Communications, 2015,pp. 1688-1696.