磁共振成像设备特定能量吸收率研究进展与计量需求

孙劼，张璞，李成伟，刘文丽

中国计量科学研究院 医学与生物计量研究所，北京 100013

引言

上世纪70年代，Lauterbur提出磁共振成像（Magnetic Resonance Imaging，MRI）的方法和实验装置[1]，经过近50年的发展，医用MRI设备（以下简称“MRI设备”）已比较普及。为提高图像信噪比，MRI设备正从低场（≤1.5 T）向高场、超高场（≥7 T）方向发展[2-3]。随着MRI设备磁场强度的增强，其射频场电磁波与人体组织相互作用也在加强，使受检者受到热损伤的风险提高，由此引发的安全问题不容忽视。

1　SAR的定义及安全限值

1.1　SAR的定义及分类

射频（Radio Frequency，RF）是高频电流通过导体产生的电磁波，频率范围在300 kHz～30 GHz之间[4]。RF与人体组织相互作用，携带的能量被组织吸收，导致局部温度升高的现象称为生物热效应。特定能量吸收率（Speci fi c Absorption Rate，SAR）是定量研究射频生物热效应的指标，其定义为生物组织单位时间、单位质量吸收射频的能量，单位为W/kg[5]。SAR可分为全身SAR和局部SAR，全身SAR指人体全身组织SAR的平均值,局部SAR指人体任意10 g组织SAR的平均值[5]。

1.2　SAR的安全限值

为保证受检者的安全，相关国际组织[6-7]起草了相应的标准、国际建议及指南，对MRI设备中SAR的安全限值做出了规定。其中，国际电工委员会（International Electrotechnical Commission，IEC）在IEC 60601-2-33中规定MRI设备射频信号在受检者体内产生SAR的安全限值（表1）[6]。美国食品药品监督管理局在其指南中规定“使用MRI设备扫描人体时，受检者头部和躯干任意1 g组织SAR的安全限值为8 W/kg”[7]。

2　电磁场数值计算与SAR仿真实验的进展

使用MRI设备扫描人体过程中，若要评估受检者体内不同组织SAR的分布情况，需先计算出设备附载人体后内部电磁场的分布状态。这需要用到电磁场数值计算方法并配合Mimics等专用软件，在给定初值与边界条件下求出Maxwell方程组的数值解，即得到人体组织内电磁场分布情况，从而得到相应区域内任一一点的SAR值。

表1　IEC 60601-2-33中规定医用磁共振成像设备SAR限值（W/kg）

2.1　电磁场数值计算方法的进展

自20世纪50年代有学者以Maxwell方程为研究对象，求出近似解析解开始，随着数学理论及计算机硬件不断升级，电磁场数值计算方法也在不断地提高和发展[8]。目前，在基本算法基础上，发展出了无单元法、小波分析法、混合算法等一系列数值计算方法[9]。伴随高性能GPU、云计算的出现，基于各种硬件技术的加速算法也成为电磁场数值计算方法的发展方向。

2.1.1时域有限差分法

时域有限差分法（Finite Difference Method，FDTD）由Yee提出[10]。计算时将Maxwell微分方程按照三维Yee元胞结构（图1）抽样离散，并在时域中对磁场和电场交替抽样。通过以上方法将Maxwell方程离散后转化为显式差分方程，并在时域内进行迭代求解[11]。FDTD是目前广泛应用的一种数值计算方法。

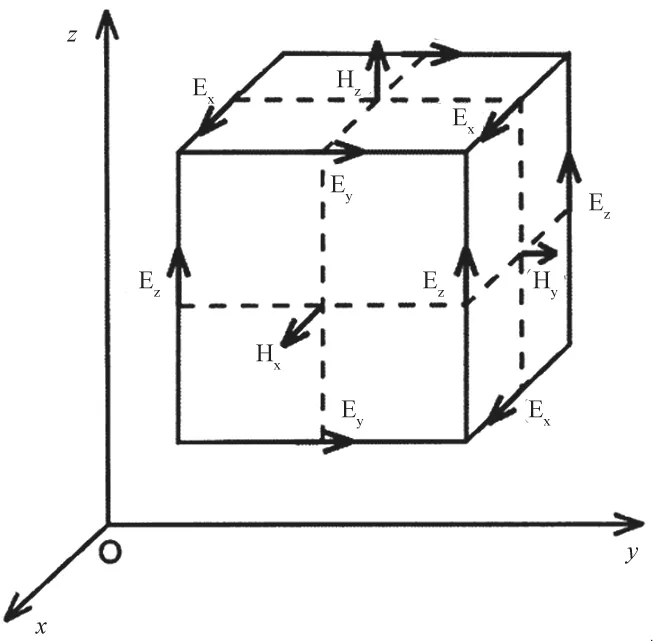
图1　三维Yee元胞结构图

2.1.2矩量法

矩量法（Method Of Moments，MOM）由Harrington在专著中提出，其原理是将频域上Maxwell积分方程组转化为近似有限求和的形式，并以此为基础建立代数方程组，通过求出代数方程组的数值进而得到电磁场中每一点磁场、电场分布的数值计算方法[12]。矩量法具有求解过程简单、步骤统一、应用便捷等优点，同时也存在着计算量大、占用大量计算机资源的缺点。目前矩量法主要应用于天线、电磁波散射等方面问题的计算。

2.1.3有限元法

有限元法（Finite Element Method，FEM）于20世纪60年代提出，Silvester最早将该方法应用于电磁场问题计算。有限元法是依据变分原理将复杂问题离散化、分解为有限多个简单问题后再分别进行求解的一种近似数值计算方法[13]。有限元法具有求解容易、收敛性好、计算程序通用性强等优点，但对无边界区域却难以求解。

2.1.4无单元法

无单元法（Element-Free Method，EFM）可突破单元域瓶颈求解复杂边界条件下的边值问题，是一种解决工程电磁场计算问题的有效新方法。无单元法由Lancaster提出，是基于滑动最小二乘法将计算场域离散成若干独立的点构造场函数，并利用初始边界条件求出数值解的方法。国外有学者使用该方法解决二维力学场边值问题[14-15]。刘素贞等[16]又将无单元法应用于电磁场数值计算研究，王立鹏等[17]尝试了基于伽辽金型无单元多重网格法，进一步解决了无单元法计算电磁场时效率不高的问题，并取得一定成效。

2.1.5小波分析法

法国工程师Morlet率先提出了小波分析的概念[18]。与传统的分析方法相比，小波分析采用的局部变换方法可对函数或信号进行多尺度细化分析，从而处理Fourier变换难以解决的问题[19]。小波分析法在电磁场数值计算中的应用主要有：小波变换和小波展开。Baharav等[20]通过对经小波变换后的阻抗矩阵方程进行压缩提高方程的稀疏性，降低运算量并提高电磁场数值计算效率。Wang[21]将小波分析中的小波展开与边界元算法相结合，提出基于多尺度小波分解的电磁场微分方程解法，用于分析多导体传输中的电磁场问题。杨仕友等[22]将一般紧支集正交小波应用于电磁场数值计算，提出一种适合处理通用边界条件的新方法，并将其成功应用于实际工程电磁场的数值计算。目前，小波基函数求解偏微分方程时边界处理问题、小波变换电磁场快速算法问题等是小波分析应用于电磁场工程领域的研究热点。

2.1.6混合算法

利用不同算法各自的优势，将不同算法应用于求解同一电磁场问题的混合算法也是电磁场数值计算的发展方向。对此，国内外学者进行了一系列研究，Braess等[23]尝试在FEM法的框架中引入多重网格法以提高问题求解效率。王海彬等[24]尝试将MOM与FDTD法混合应用于计算脉冲照射电磁场中人体头部不同部位SAR值。李莉等[25]将FEM与边界元法混合应用于求解包含运动导体的二维电磁场计算。

2.1.7基于硬件技术的加速算法

基于GPU（Graphic Processing Unit，GPU）的加速算法图形处理器是用于图像信息处理与生成的专用处理器。与CPU相比，GPU更适用于流处理计算。GPU性能不断增强，其内部的可编程浮点单元运算能力提高，使其适于处理具有“计算密集型”特点的问题[26]。在电磁学领域，为提高电磁场计算效率，开发各种基于GPU的加速算法已成为研究热点。Krakiwsky等[27]尝试利用GPU对FDTD算法进行加速。我国学者杨正龙等[28]在物理光学和物理绕射理论基础上，开发基于GPU的射线追踪算法，该方法可用于快速计算具有凹腔结构目标的电磁散射问题。

基于云计算的加速算法云计算是随着互联网发展产生的新型商业化计算服务模式。云计算具有使用维护成本低、计算资源利用率高等优点。基于云计算的加速算法已应用于电磁场计算中，杨亮[29]将云计算与并行算法相结合，将电磁场空间划分为多个子空间，使用多个CPU并行计算各个子空间内电磁场,将全部计算结果合并得到整个空间的电磁场分布。金亮[30-31]将云计算技术引入电磁场耦合问题计算中，搭建了基于OpenMPI方法的云计算平台，并在该平台上实现电磁场高效并行计算。

2.2　医用磁共振设备SAR仿真研究进展

2.2.1人体模型研究进展

上世纪90年代起，已有Slavin等[32]开始研制人体解剖学数字化模型并将其应用于医学仿真。早期的人体数字化模型大都基于志愿者和病人的CT扫描图像建立，主要用于医用辐射物理学的相关研究。由于这类模型对软组织分辨率不高，因此，不适于对人体不同介电性质的软组织进行仿真。为此，Nagaoka等[33]通过磁共振成像建立了日本成年男性和成年女性的高分辨率全身模型，模型包括51个不同组织，可用于射频电磁场下的人体仿真。Lee等[34]统计了年龄在18～24岁之间韩国成年男性的平均体格数据，并选择一名男性志愿者通过其磁共振图像建立包含30种不同组织结构的人体模型。Christ等[35]基于高分辨率磁共振图像建立了一组称为“Virtual Family”的解剖学人体模型（其中包括一名成年男性、一名成年女性以及两名儿童），这组模型具有80多种不同组织结构，可用于各类电磁环境暴露仿真评估。Szczerba等[36]基于几何图像拓扑改进“Virtual Family”人体模型解决其图形质量和一致性问题。Wu等[37]研究建立了可用于电磁环境仿真的基于中国人体质的解剖学人体模型，包括一名成年男性（含87种组织结构）和一名成年女性（含90种组织结构）。随后，Li等[38]利用磁共振成像建立了婴儿（12个月）模型（含32种组织结构）。

2.2.2仿真实验研究进展

为研究不同磁场强度、不同类型线圈、不同扫描序列条件下，人体组织中SAR分布情况，研究人员采用前文所介绍的电磁场数值计算方法，结合计算机技术利用Mimics等专用软件，对线圈和人体组织进行计算机建模仿真研究。Wolf等[39]通过仿真实验，给出可用于高场强MRI设备SAR仿真的人体模型简化方法。Cornelis等[40]用FDTD算法仿真计算出3 T MRI设备上使用体线圈扫描人体时B1场分布，并将仿真结果与实际测量值比较发现两者之间存在相关性，验证该仿真方法可行。Ibrahim等[41]采用FDTD法对鸟笼线圈下人体头部的SAR值进行仿真计算，结果表明SAR值分布与人体组织特性有关。Neufeld等[42]通过仿真“Virtual Family”人体模型在3 T场强MRI设备上，分别使用多源发射体线圈和传统体线圈扫描时，模型内部各组织SAR分布情况，研究多源发射体线圈的安全性。仿真结果表明目前应用于强场MRI设备的多源发射体线圈可导致更多热量沉积，存在更大的安全风险。

曾雁冰等[43]基于仿真方法建立鸟笼线圈与女性盆腔模型，利用FDTD算法计算该模型在64 Hz射频条件下的SAR值分布，找出局部热损伤风险较高的组织。黄绮华等[44]利用FDTD算法对磁场强度分别为1.5 T、3 T和7 T的MRI设备扫描人体时，B1场均匀性和SAR分布进行仿真计算，研究人体内部B1场均匀性、SAR分布随MRI设备磁场强度的变化规律。仿真结果表明：当MRI设备场强从1.5 T分别增加到3 T和7 T时，B1场的均匀性逐渐降低，人体各组织SAR的平均值逐渐增高。

3　MRI设备SAR计量需求

随着我国经济发展和医疗服务需求的持续增长，各类医疗机构中MRI设备装机量不断增加。MRI设备数量的增多、新设备的投入以及大量使用多年的在用设备，这些都对MRI设备使用中安全风险防护提出更高的要求。如何准确计量SAR并对MRI设备的安全性进行评估，降低受检者的热损伤几率，是安全风险防护中的重点，也是医生和受检者普遍关注、需要解决的问题。对MRI设备进行科学有效的计量溯源是解决上述问题的有效方法。

3.1　开展计量的政策依据

国务院2014年6月实施的《医疗器械监督管理条例》及药监总局2016年2月实施的《医疗器械使用质量监督管理办法》中均规定对MRI设备这类需要定期检查、检验、校准、保养、维护的医疗器械，“应当按照产品说明书的要求进行检查、检验、校准、保养、维护”，这是对医疗机构中在用MRI设备开展周期性计量校准的政策依据。

3.2　MRI设备质控的计量需求

医疗设备质控以规避医疗设备风险为出发点，以医疗设备全生命周期的质量保障为目标，以技术性检测为基础手段，以完整的管理流程为执行标准，以数据收集和分析为持续改进方向和管理工作，是医院质量管理的重要组成部分。MRI设备属于医院医疗设备质控重点关注的大型设备，对其进行周期性计量校准是日常质控的重要技术手段。

3.3　MRI设备基本计量需求

（1）磁体系统性能计量需求。磁体系统由主磁体、梯度线圈和射频线圈组成，作为MRI设备中主要部件其磁场强度数值直接影响设备扫描图像的真实性和有效性，需准确计量。

（2）成像质量计量需求。MRI设备作为影像设备其信噪比、均匀性、空间线性、空间分辨力、低对比度分辨力等成像质量指标均需计量校准。

3.4　MRI设备SAR计量需求

（1）技术规范需求。国内部分经济发达省份针对医用MRI设备起草了地方计量检定规程或校准规范，规定了MRI设备磁场强度、成像质量的计量要求及各参数的计量方法。但上述规范中对MRI设备重要安全指标SAR的计量性能未作规定，也未给出科学有效的SAR计量方法，这影响到SAR计量校准工作的开展。

（2） 计量设备需求。SAR计量设备包括通用模型 （受体）及精确测量SAR值的专用测量装置。通用模型由模拟人体不同部位（头部、躯干）轮廓的壳体及内部仿真溶液构成，用于模拟实际扫描时受检者人体组织。SAR值专用测量装置是测量MRI设备空间中每一点上SAR值的专用测量设备。目前国内缺乏符合中国人生理特征的SAR计量通用模型及SAR测量装置，无法对受检者受检时体内能量沉积和升温的情况进行有效评估，这影响到SAR计量校准工作的开展。研制MRI设备SAR计量通用模型，搭建SAR测量装置，实现对MRI设备SAR值的精确计量是目前亟待解决的问题，需要进一步深入研究。

4　总结

SAR作为评价MRI设备射频生物热效应的量化指标成为研究热点。基于电磁场数值计算方法的计算机仿真实验是研究SAR的有效方法。对MRI设备SAR的计算仿真、并以有效计量溯源保证仿真数据准确，有助于进一步量化研究相关设备射频在人体组织内生物热效应，有效降低受检者的安全风险。

[参考文献]

[1] Lauterbur PC.Image formation by induced local interactions:Examples of employing nuclear magnetic resonance[J].Nature,1973:242(5394):190-191.

[2] Edelstein WA,Glover GH,Hardy CJ,et al.The intrinsic signal to noise ratio in NMR imaging[J].Magn Reson Med,1986,3(4):604.

[3] 杨保联.超高场磁共振人体成像应用研究和医学前景[J].波谱学杂志,2015,32(4):707-714.

[4] 姜晓强,张鹏高,王成发.射频技术发展与应用现状[J].信息通信,2012,(3):206.

[5] 毕帆,王龙辰,李斌.MR射频能量特定吸收率的计算及其临床应用[J].中国医疗器械杂志,2014,38(6):423-426.

[6] IEC 60601-2-33,Particular Requirements for the Basic Safety and Essential Performance of Magnetic Resonance Equipment for Medical Diagnosis[S].Intemational Electrotechnical Commission,2013.

[7] FDA CDRH Guidance 793,Guidance for Industry and FDA Staff: Criteria for Signi fi cant Risk Investigations of Magnetic Resonance Diagnostic Devices[S].FDA,2003.

[8] 关海爽,马文阁.电磁场数值计算新方法的研究[J].辽宁工业大学学报(自然科学版),2006,26(4):230-233.

[9] 赵云芳,王红霞,竹有章,等.电磁场数值计算方法[A].陕西省物理学会2008年学术年会[C].2008.

[10] Yee KS.Numerical solution of initial boundary value problems involving maxwell’s equations in isotropic media[J].IEEE T Antenn Propag,1966,14(3):302-307.

[11] 葛德彪,闰玉波.电磁波时域有限差分方法[M].西安:西安电子科技大学出版社,2005.

[12] Gibson WC.The Method of Moments in Electromagnetics[M].Pmladelphia:Taylor &Francis,2007.

[13] Jin J.The Finite Element Method in Electromagnetics[M].New York:Wiley,1993．

[14] Nayroles B,Touzot G,Villon P.Generalizing the fi nite element method: diffuse approximation and diffuse elements[J].Comput Mech,1992,10(5):307-318.

[15] Lei Y,Friswell MI,Adhikari S.A Galerkin method for distributed systems with non-local damping[J].Int J Solids Struct,2006,43(11-12):3381-3400.

[16] 刘素贞,杨庆新,陈海燕,等.无单元法在电磁场数值计算中的应用研究[J].电工技术学报,2001,16(2):30-33.

[17] 王立鹏,王欣彦,唐任远.EFG-MG法及其在电磁场数值计算中的应用[J].电工技术学报,2010,25(1):1-5.

[18] 邓东皋,彭立中.小波分析[J].数学进展,1991,20(3):294-310.

[19] 彭玉华,董晓龙.小波变换在电磁场数值计算中的应用[J].电子学报,1996,24(12):46-52.

[20] Baharav Z,Leviatan Y.Impedance matrix compression using adaptively constructed basis functions[J].IEEE T Antenn Propag,1996,44(9):1231-1238.

[21] Wang G.On the utilization of periodic wavelet expansions in the moment methods[J].IEEE T Antenn Propag,1995,43(10):2495-2498.

[22] 杨仕友,倪米正.小波—伽辽金有限元法及其在电磁场数值计算中的应用[J].中国电机工程学报,1999,(1):56-61.

[23] Braess D,Verfurth R.Multigrid methods for nonconforming fi nite element methods[J].Siam J Numer Anal,1990,27(4):979-986.

[24] 王海彬,牛中奇.MOMTD/FDTD混合法分析线天线与近场媒质的相互作用[J].微波学报,2007,23(3):5-9.

[25] 李莉,潘杰,朱翠霞,等.有限元—边界元耦合法在二维电磁场数值计算中的应用及优化措施[J].山东师范大学学报(自然科学版),2013,28(3):59-65.

[26] 吴恩华,柳有权.基于图形处理器(GPU)的通用计算[J].计算机辅助设计与图形学学报,2004,16(5):601-612.

[27] Krakiwsky SE,Turner LE,Okoniewski MM.Graphics processor unit (GPU) acceleration of finite-difference time-domain(FDTD) algorithm[A].International Symposium on Circuits and Systems[C].New York:IEEE,2004:265-268.

[28] 杨正龙,金林,李蔚清.基于GPU的图形电磁计算加速算法[J].电子学报,2007,35(6):1056-1060.

[29] 杨亮.云计算与电磁仿真结合的可行性分析[J].电子技术与软件工程,2014,(2):29-30.

[30] 金亮,邱运涛,杨庆新,等.基于云计算的电磁场有限元计算方法研究[J].中国科技论文,2016,11(11):1310-1314.

[31] 金亮,邱运涛,杨庆新,等.基于云计算的电磁问题并行计算方法[J].电工技术学报,2016,31(22):5-11.

[32] Slavin KV.The visible human project[J].Sur Neur,1997,48(6):638.

[33] Nagaoka T,Watanabe S,Sakurai K,et al.Development of realistic high-resolution whole-body voxel models of Japanese adult males and females of average height and weight, and application of models to radio-frequency electromagnetic- fi eld dosimetry[J].Phys Med Biol,2004,49(1):1-15.

[34] Lee,Ae-kyoung,Choi WY,et al. Development of korean male body model for computational dosimetry[J].ETRI J,2006,28(1):107-110.

[35] Christ A,Kainz W,Hahn EG,et al.The Virtual familydevelopment of surface-based anatomical models of two adults and two children for dosimetric simulations[J].Phys Med Biol,2010,55(2):N23.

[36] Szczerba D,Neufeld E,Zefferer M,et al.Unstructured mesh generation from the Virtual Family, models for whole body biomedical simulations[J].Pro Comput Sci,2010,1(1):837-844.

[37] Wu T,Tan L,Shao Q,et al.Chinese adult anatomical models and the application in evaluation of RF exposures[J].Phys Med Biol,2011,56(7):2075-2089.

[38] Li C,Chen Z,Yang L,et al.Generation of infant anatomical models for evaluating electromagnetic field exposures[J].Bioelectromagnetics,2015,36(1):10-26.

[39] Wolf S,Diehl D,Gebhardt M,et al.SAR simulations for highfi eld MRI: how much detail, effort, and accuracy is needed[J].Magnet Reson Med,2013,69(4):1157-1168.

[40] Cornelis VDB,Bartels LW,Van BB,et al.The use of MR B+1 imaging for validation of FDTD electromagnetic simulations of human anatomies[J].Phys Med Biol,2006,51(19):4735-4746.

[41] Ibrahim TS,Lee R,Baertlein BA,et al.B1 field homogeneity and SAR calculations for the birdcage coil[J].Phys Med Biol,2001,46(2):609.

[42] Neufeld E,Gosselin MC,Murbach M,et al.Analysis of the local worst-case SAR exposure caused by an MRI multi-transmit body coil in anatomical models of the human body[J].Phys Med Biol,2011,56(15):4649.

[43] 曾雁冰,周宇佳,黄绮华,等.MR射频能量特定吸收率在女性盆腔不同组织中分布规律的研究[J].中国医学物理学杂志,2012,29(5):3632-3637.

[44] 黄绮华,高勇,辛学刚.高场和超高场MR下人体内B_1场均匀性及SAR随场强变化规律的研究[J].中国生物医学工程学报,2013,32(1):21-27.

本文编辑 王婷