一种变步长LMS算法提取胎儿心电

袁丽，吴水才，袁延超，高小峰

1.北京工业大学 生命科学与生物工程学院，北京 100124；2.北京麦迪克斯科技有限公司，北京 100095

引言

心电图是医生用来识别人体心脏活动是否异常的重要工具，胎儿心电图也可跟踪胎儿的心脏健康状况。胎儿心电信号中含有的潜在信息，可以有效的帮助临床医生在孕妇怀孕期间或分娩时做出合适和及时的决策。目前获取胎儿心电有两种方法：一种是侵入式的头皮电极法，该方法可以直接测得较纯净的胎儿心电信号，但它的局限性是只能在分娩时去检测胎儿心电信号，并且它还是有创检测，极有可能给母亲和胎儿造成伤害；另一种方法是非侵入式的腹部电极法，通过在母体腹部放置电极片来采集腹部体表信号，该方法可以在妊娠期进行长期的监护，不会对母亲和胎儿造成伤害。但孕妇腹部体表信号十分复杂，不仅包含微弱的胎儿心电和母体心电，还包括了母亲的呼吸噪声、工频干扰等信号[1]。特别是腹部信号中母体心电的幅值往往是胎儿心电的2～10倍[2]，这就导致了胎儿心电的提取十分困难，因此需要研究出一种能够有效提取胎儿心电的方法。

目前，国内外常用的胎儿心电提取算法主要有自适应滤波[3-4]、小波分析[5]、匹配滤波法[6]、盲源分离[7]、独立成分分析[8]、神经网络[9-10]及奇异值分解[11]等。其中，自适应滤波方法在进行滤波的时候可以采用最小均方（Least Mean Square，LMS）算法或者递推最小二乘（Recursive Least Squares，RLS）算法。与RLS算法相比，LMS算法计算量较小，实时性较好，并且便于根据实际问题进行调整与改进，应用范围较广。然而LMS算法的最大缺点就是收敛速度和稳态误差之间的矛盾，要使收敛速度加快就必须增大步长，但这样又会引起稳态误差增大；要降低稳态误差就必须减小步长，这又会使收敛速度变慢。为了解决这一矛盾，我们采用变步长LMS算法，在初始收敛阶段，选择较大步长，以便有较快的收敛速度与跟踪速度，而在算法收敛后，选择较小的步长，从而降低稳态误差。本文算法利用当前误差与上一步误差的自相关估计来控制步长的更新，消除了不相关噪声序列的干扰，步长迭代是基于反正切函数。此改进算法在收敛速度、跟踪能力和稳态误差方面均优于传统LMS算法，并且可以准确快速的从腹部混合信号中提取出胎儿心电。

1　传统LMS算法

20世纪70年代，维德罗等[12]提出自适应滤波及其算法，这种随机梯度算法被称为LMS算法，因其计算量少，易于实现而得到了广泛的应用。自适应滤波器模型，见图1。

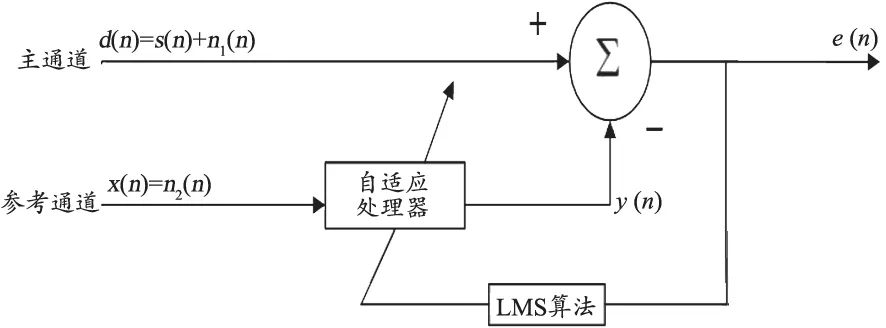
图1　自适应滤波器模型

图1中d(n)为主通道的原始输入信号，通常包含目标信号s(n)与噪声信号n1(n)，目标信号s(n)与噪声信号n1(n)是不相关的。参考通道输入的信号x(n)是d(n)的一种度量，以某种方式与噪声信号n1(n)相关。x(n)经过滤波器处理，得到的输出信号y(n)是噪声信号n1(n)的估计值，这样从d(n)中减去y(n)，得到的e(n)就是目标信号s(n)的估计值。由图1可知，e(n)在自适应滤波器中有两种作用，一是目标信号s(n)的最佳估计，二是控制自适应滤波器的输出y(n)。基于最速下降法的LMS算法迭代公式[13]如下：

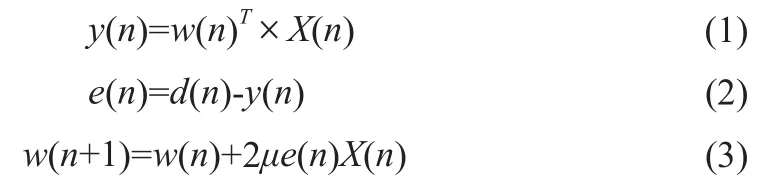
式(1)与式(3)中X(n)=[x(n),x(n-1),…x(n-m+1)]T，m表示滤波器的阶数，式(3)中μ为步长因子，保证算法收敛的μ值范围是0≤μ≤1/λmax，其中λmax为自相关矩阵的最大特征值。如果μ为固定值，则LMS算法为固定步长LMS算法。

将固定步长LMS算法应用到胎儿心电信号提取中，x(n)为母体胸部信号，d(n)为母体腹部采集到的混合信号，由自适应滤波器得到的误差信号e(n)就是胎儿心电信号的估计值。固定步长LMS算法提取胎儿心电信号的流程归纳如下：① 参数初始化，初始化步长因子μ，0≤μ≤1/λmax，初始化权系数向量w，w是一个m×1的列向量，m表示滤波器的阶数；② 输入两通道信号，腹部混合信号作为原始输入信号d(n)，胸部信号作为参考输入信号x(n)；③ 对于n=m,m+1,.......N进行式(1)、式(2)、式(3)运算，寻找最佳权系数向量；④ 由最佳权系数向量得到的误差信号e(n)就是所要提取的胎儿心电信号的最佳估计值。

2　变步长LMS算法

初始收敛速度、跟踪能力以及稳态失调是衡量LMS算法性能的3个最重要的技术指标[14]。由于主输入端不可避免地存在干扰噪声，LMS算法将产生参数失调噪声。干扰噪声越大，则引起的失调噪声就越大。减小步长因子可减小LMS算法的稳态失调噪声，提高算法的收敛精度。然而步长因子的减小将降低算法的收敛速度和跟踪速度。因此，固定步长的LMS算法在收敛速度和稳态误差方面是相互矛盾的。为了解决这一问题，本文选择变步长LMS算法来提取胎儿心电，算法利用当前误差与上一步误差的自相关估计来控制步长的更新，这样可以消除不相关噪声序列的干扰，步长递推公式是基于反正切函数。

变步长LMS算法的输出信号如式(4)所示：

其中X(n)=[x(n),x(n-1),…x(n-m+1)]T是输入信号，m表示滤波器的阶数，w(n)为权系数列向量量，维数为m×1。误差信号e(n)可由下式表示：

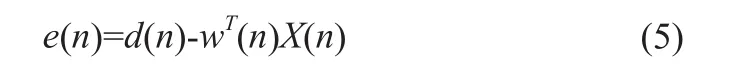
算法的核心步骤就是步长的迭代，与收敛速度和稳态误差有关，步长迭代是基于反正切函数的，如下式所示：

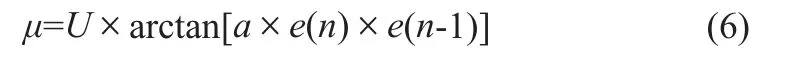
式(6)中U与a均为大于0的常数，e(n)是当前误差值，e(n-1)是上一步误差值。权系数向量的更新递归公式为：

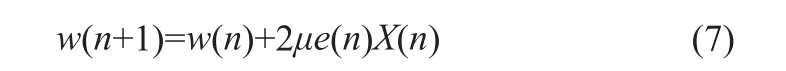
为了比较本文算法与LMS算法的性能，我们采取仿真实验来比较两种算法在收敛速度、跟踪能力、稳态误差等方面的性能。选择自适应滤波器阶数为m=2，系统的初始权向量为w=[0.8,0.5]T，输入信号x(n)为零均值单位方差的高斯随机信号，噪声v(n)为与x(n)不相关的高斯白噪声，其均值也为零。采样点数为1000，实验500次，两种算法得到如下所示的学习曲线。

从本文算法与传统LMS算法学习曲线（图2）中可以看出，本文算法在收敛速度与跟踪速度方面均比LMS算法快，在稳态误差相差不大的情况下，本文提出的算法在抗干扰能力、收敛速度、跟踪能力方面具有明显的优势，性能有着明显的提高。

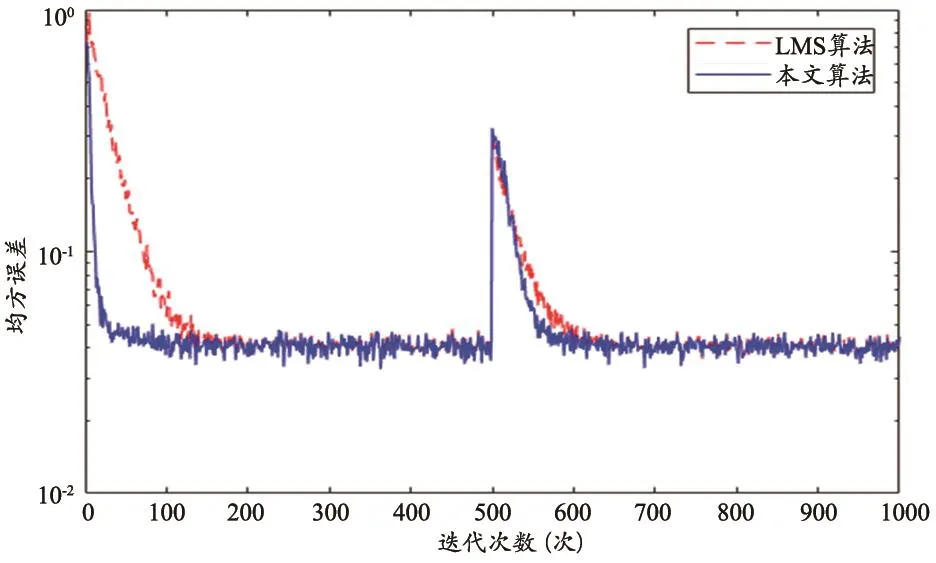
图2　本文算法与传统LMS算法学习曲线

3　算法验证及胎儿心电提取

将母体腹部信号作为原始输入信号，母体胸部信号作为参考输入信号，使用本文设计的变步长LMS算法进行胎儿心电的提取，对提取出来的胎儿心电信号用带通滤波器进行去噪，最后得到较为纯净的胎儿心电信号。

把本文算法应用于胎儿心电信号的提取，采用DaISy（Database for the Identi fi cation of Systems）数据库[15]。该数据库中的数据是通过电极片从孕妇腹部采集记录心电，采样频率为250 Hz，采集时间为10 s，共2500个采样点。该组数据共有8个通道信号，前5个通道是腹壁混合导联数据，后3个通道为母体胸部导联数据。

选择第1通道腹部混合信号作为原始输入信号，选择第8通道胸部信号作为参考信号，分别用本文设计的变步长LMS算法与LMS算法进行胎儿心电提取，实验结果，见图3、图4。

图4　传统LMS算法提取胎儿心电

从图3中可以看出胎儿心电QRS波完全被提取出来，提取出来的胎儿心电几乎不含有母体心电。图4是直接用传统LMS算法提取出来的胎儿心电，当胎儿心电和母体心电完全重合时，传统LMS算法没有将胎儿心电提取出来。

下面使用其他通道心电数据做算法验证，本文算法提取出来的胎儿心电信号，可以得到清晰的胎儿心电信号，并且没有遗失R波。当母体胸部信号与胎儿信号重合时，该算法的提取效果不是很好。通过比较可以看出本文算法在提取胎儿心电方面准确度比LMS算法高。

为了进一步验证本算法的性能，选择Outram[16]提出的基于特征值的信噪比和基于互相关系数的信噪比在客观上对本文算法与LMS提取效果进行评价，信噪比值越大，提取效果越好。

第一步，首先对提取的胎儿心电R波检测，以每个R波为基准，截取M段长度均为N的信号段，保证每一个信号段都可以包含一个完整的QRS波；然后以M段信号为列，构成矩阵UN×M，并对矩阵的每列数据进行均值为零，方差为1的归一化处理。则基于特征值的信噪比公式：

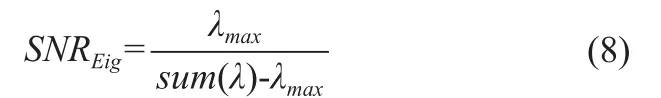
其中λ是矩阵UTU的M个特征值，λmax是矩阵UTU的特征值的最大值。

第二步，基于互相关系数信噪比公式：

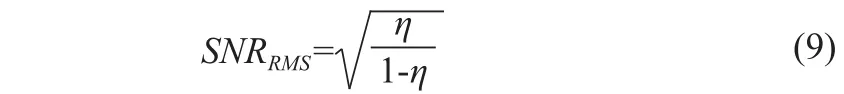
LMS算法与本文算法计算得到的信噪比数值，见表1。对比可得，本算法在特征值和互相关系数信噪比上均优LMS算法。

表1　两种算法信噪比值

4　讨论与结论

为了可以长期的无伤害的监护胎儿的发育状况，目前国内外都是通过在母体腹部放置电极片来采集腹部体表信号，但是通过电极片从孕妇腹部采集到的混合信号，不仅包括了母体心电和胎儿心电，也包括了一些其他的干扰信号。由于传统LMS算法计算量较小，实时性好，在胎儿心电提取方面得到了广泛的应用。但是传统LMS算法收敛速度与稳态误差之间存在着矛盾，为了解决这个问题，本文采用变步长LMS算法提取胎儿心电信号，算法利用当前误差与上一步误差的自相关估计来控制步长的更新，可以消除一些不相关噪声序列的干扰，本文算法的步长迭代是基于反正切函数。由于本文算法计算量较小，在实时提取胎儿心电方面有很大的应用前景。

本文提出的变步长LMS算法解决了传统LMS收敛速度与稳态误差之间的矛盾，可以提取出清晰的胎儿心电。经过仿真实验与胎儿心电提取实验验证，本文算法在性能和提取效果上均优于传统LMS算法。另外，与其他算法相比，该算法计算量较少，保持了较高的实时性。实验结果表明，该算法可以提取出来比较清晰的胎儿心电信号，适合做实时处理。

[参考文献]

[1] 占海龙.单导联和多导联环境下胎儿心电分离算法研究[D].杭州:杭州电子科技大学,2013.

[2] 刘清欣,万红.基于快速定点独立分量分析算法的母胎心电信号分离[J].生物医学工程研究,2007,26(1):37-41.

[3] Prasad DVD,Swarnalatha R.A new method of extraction of FECG from abdominal signal[J].IFMBE P,2009,23:98-100.

[4] Taralunga D,Gussi I,Strungaru RF,et al.ECG enhancement:Adaptive power line interference cancellation based on Hilbert Huang Transform[J].Biomed Signal Proces Cont,2015,19:77-84.

[5] Wu S,Shen Y,Zhou Z,et al.Research of fetal ECG extraction using wavelet analysis and adaptive filtering[J].Comput Biol Med,2013,43(10):1622-1627.

[6] Dessì A,Pani D,Raffo L.An advanced algorithm for fetal heart rate estimation from non-invasive low electrode density recordings[J].Physiol Meas,2014,35(8):1621-1636.

[7] Blumensath T,Davies ME.Blind separation of maternal and fetal ECG recordings using adaptive sparse representations[A].Proceedings of ICA Research Network International Workshop[C].2006.

[8] 李朝兰,方滨,李慧杰,等.应用自相关和独立分量分析的胎儿心电信号提取[J].中国医学物理学杂志,2016,33(8):838-843.

[9] Sait NA,Thangarajan M,Snehalatha U.Neural network based on verilog HDL for fetal ECG extraction[J].Int J Biomed Res,2016,7(10):698-701.

[10] Agarwal N,Prasad DV,Swarnalatha R.Extraction of Fetal Electrocardiographic Signals Using Neural Network[M].Berlin:Springer,2010:1350-1353.

[11] Ayat M,Assaleh K,Nashash H,et al.ECG extraction from a single abdominal ECG signal using SVD and polynomial classifiers[A].Machine Learning for Signal Processing,2008.IEEE Workshop on IEEE[C].2008:250-254.

[12] Diniz PSR,de Campos MLR,Antoniou A.Analysis of LMSNewton adaptive fi ltering algorithms with variable convergence factor[J].IEEE T Signal Proces,1995,43(3):617-627.

[13] Glentis G,Berberidis K,Theodoridis S.Ef fi cient least squares adaptive algorithms for FIR transversal fi ltering[J].IEEE Signal Proc Mag,1999,16(4):13-41.

[14] 亢润东.一种基于S形函数的LMS算法仿真研究[J].数字技术与应用,2013(2):106-107.

[15] Leuven KU,Moor BD,Gersem PD,et al.DAISY: A database for identi fi cation of systems[J].Tech Rep,1997,38:4-5.

[16] Outram NJ.Intelligent Pattern Analysis of the Fetal Electrocardiogram[D].Plymouth:University of Plymouth,1997.