快速多维标度算法研究*

屈太国，蔡自兴

1.衡阳师范学院 计算机科学与技术学院，湖南 衡阳 421002

2.智能信息处理与应用湖南省重点实验室，湖南 衡阳 421002

3.中南大学 信息科学与工程学院，长沙 410083

1　引言

随着大数据时代的到来，数据规模越来越大[1]，数据高维化趋势越来越明显，这带来了一系列问题，如“维数灾难”[2]。数据降维是应对数据高维化的一种有效方法。

经典多维标度法（classicalmultidimensionalscaling，CMDS）基于样本之间的距离，求它们在低维欧氏空间中的坐标，使它们在欧氏空间的距离尽量逼近原来的距离[3]。CMDS是数据降维和数据可视化的常用方法[4-8]，被广泛应用于Matlab、SAS、SPSS、Statistica、S-Plus等计算机语言中。

CMDS的优点是具有解析解，缺点是速度慢。它的处理时间为Θ(N3)，其中N表示样本个数。随着数据（样本）规模越来越大，提高CMDS的速度成为一个迫切需要解决的问题。人们提出了多种CMDS的快速算法。文献[9-11]基于弹簧-质点模型（springmass model），通过最小化代价函数（cost function），求样本在低维欧氏空间的坐标。Chalmers算法[9]的时间为Θ(N2)；Morrison算法[10]将时间减少到Θ(NlgN)，但它只能给出样本在二维欧氏空间的坐标；Williams等人[11]对Chalmers算法进行了一些改进，使之能适应高维大规模样本集。这3种算法都属于迭代算法，容易陷入局部最小。另一类快速算法[12-15]属于Nystrom算法[16]。其中FastMap[12]将样本投影到一组相互正交的枢轴（pivot）上，这些投影构成了样本在低维欧氏空间中的坐标。HyperMap[13]对FastMap进行了推广，提供了“多视角”分析数据的灵活性。MetricMap[14]将目标空间由FastMap中的欧氏空间推广到伪欧氏（pseudo-Euclidean）空间。LMDS（landmark multidimensional scaling）[15]首先指定部分样本为标志点（landmark point），利用CMDS求解标志点之间的距离矩阵，得到标志点在低维空间的坐标，其余点的坐标由一个线性公式给出。上述所有算法在速度上都比CMDS快，但给出的都是近似解。因此，如何快速求得与CMDS完全一致的解仍有待研究。

作者先后提出了一种改进的FastMap算法（improved FastMap，iFastMap）[17]和基于分治策略的多维标度算法（divide-and-conquer based MDS，dcMDS）[18]。这两种算法和本文提出的iLMDS（improved LMDS）算法都能快速得到与CMDS一致的解。

2　预备知识

CMDS从样本集的距离矩阵出发，求样本在欧氏空间中的坐标，使它们在欧氏空间的距离尽量逼近原来的距离。

本文将距离限定为欧氏距离，即存在正整数m和x1,x2,…,xN∈Rm，满足：

其中，xi=(xi1,xi2,…,xim)T，i=1,2,…,N表示样本的坐标，N表示样本集的大小；dij表示样本间的欧氏距离。

本文采用X=(xij)=(x1,x2,…,xN)、D=(dij)分别表示样本集的坐标矩阵和距离矩阵。在CMDS问题中，已知的是距离矩阵，而坐标矩阵往往是未知的，但这个未知量在快速多维标度算法的讨论中起到非常关键的作用。

基于距离矩阵，可以构造下面两个矩阵：

其中：

通过对矩阵B进行谱分解可以得到CMDS的解析解（如表1），本文称之为样本的CMDS坐标。类似的，本文中其他算法的结果，都称为相应算法的坐标。为区别起见，称X为样本集的原始坐标矩阵。

CMDS需要对矩阵B进行谱分解，其时间复杂度为Θ(N3)。随着样本规模的扩大，CMDS的时间急剧增加，从而限制了其在大规模样本集上的应用。

2.1　CMDS和PCA的等价关系

主成分分析（principal component analysis，PCA）是另一种常用的多元数据分析方法。它从样本集的坐标矩阵出发，旨在找到样本方差最大的方向，然后把样本投影到这些方向上。这些投影构成PCA坐标。

CMDS与PCA算法归纳如下，见表1。

Table 1　CMDS and PCA表1　CMDS和PCA

由表1可知，PCA坐标是通过对协方差矩阵Σ=(XH)(XH)T进行谱分解得到的。

令Λm=diag(λ1,λ2,…,λm)，UX=(u1,u2,…,um)，则协方差矩阵可以写成如下谱分解的形式：

X的PCA坐标矩阵可以写成如下矩阵形式：

其中，u1,u2,…,um是方差最大的方向，称为样本集的主轴向量；UX=(u1,u2,…,um)称为X的主轴矩阵。

根据文献[3]，对欧氏距离，样本集的CMDS坐标矩阵与PCA坐标矩阵相等，即：

这表明：CMDS坐标从本质上可视为样本在各主轴向量上的投影，也可视为对原始坐标的一种变换。这种变换属于下面要介绍的保距变换。

2.2　保距变换

定义1（保距变换）给定常向量r∈Rm和m阶正交矩阵O，如下变换称为保距变换[20]：

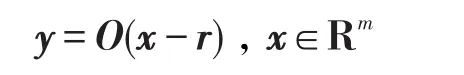
用二元组表示。y称为x在下的像。不难验证，任意两点间的欧氏距离在变换前后保持不变。

对样本集X=(x1,x2,…,xN)，令Y=(y1,y2,…,yN)，其中yi=O(xi-r)，可得X在下的像矩阵Y=

关于保距变换，有如下定理。

定理1坐标矩阵与其像矩阵具有相同的PCA坐标矩阵。

证明假定X为m×N矩阵，r∈Rm，O为m阶正交矩阵，Y为X在下的像矩阵，即Y=O(X-由1TNH=0可知：

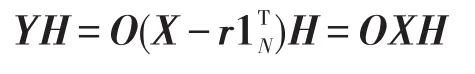
由此可得Y的协方差矩阵：

在上式证明中用到了式（4）。令UY=OUX，有：

上式就是ΣY的谱分解。根据式（5），可得Y的PCA坐标矩阵：

定理1表明，如能得到X的像矩阵，则只需对它进行PCA就可以得到样本集的CMDS坐标。

与CMDS基于整个样本集的距离信息不同，本文介绍的3类算法利用样本集上满足特定条件的某个子集的距离信息，得到X的像矩阵，从而求得与CMDS完全一致的解，并且提高了速度。下面介绍的内在维数规定了样本子集所需满足的条件。

2.3　样本集的内在维数

定义2（内在维数[21]）样本集内在维数指的是包含样本集上所有点的最小欧氏空间的维数。

根据文献[21]，rank(XN-1-xN1TN-1)就是样本集内在维数，其中XN-1=(x1,x2,…,xN-1)，1N-1表示分量均为1的N-1维列向量。

不难验证：

根据式（3），有：

本文采用m表示样本集的内在维数，即：

为了得到一个内在维数等于m的子集，可以从样本集中随机抽取部分点。本文采用最简单的策略，即抽取前n个样本。显然，内在维数等于m的子集至少包含m+1个样本，即n≥m+1。如果子集的内在维数小于m，逐步增加n的值，直至子集内在维数等于m。这就是本文要采用的子集选择算法。

算法1子集选择算法

输入：距离矩阵D=(dij),内在维数m。

输出：n。

1.令n=m+1；

2.利用式（6）计算前n个点的内在维数m1；

3.如果m1=m，返回n，否则，n=n+1，转2。

3　快速多维标度算法

首先回顾两种快速多维标度算法iFastMap和dcMDS，然后介绍一种新的快速算法iLMDS。iFast-Map、iLMDS分别为FastMap和LMDS的改进算法。

3.1　iFastMap算法

FastMap算法包含多次投影，每次投影包含3步：首先，选取两个相距较远的样本构成一个枢轴；然后，利用余弦定理，将各样本投影到枢轴上；最后，修改样本之间的距离。

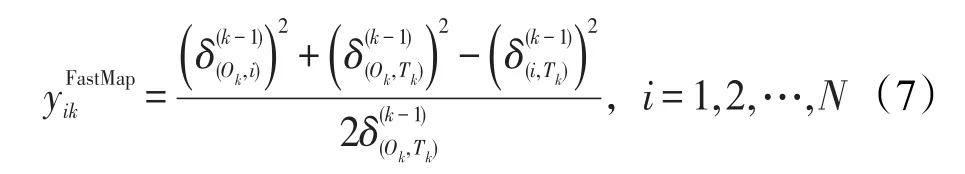
第k次投影后，各点之间的距离为:

FastMap算法的时间主要用于距离的计算，每次投影后，要重新计算所有样本之间的距离，因此s次投影需要的时间为Θ(sN2)。

FastMap算法可以概括为：在整个样本集上找到m个枢轴，投影、修改所有样本之间的距离。

其中，UF=(e1,e2,…,em)，e1,e2,…,em为各枢轴上的单位向量，彼此正交；r取决于各枢轴的起点坐标。

式（9）表明，寻找枢轴的本质是得到m个彼此正交的单位向量。根据文献[17]，寻找枢轴的范围可以从整个样本集缩小到一个内在维数等于m的子集上。

其次，根据式（7），在计算坐标时，只用到了各点与枢轴点之间的距离。换句话说，每次投影后，修改所有样本间的距离是不必要的。因此，如果能事先确定各枢轴，可以大大减少距离的计算。

最后，根据式（9），YFastMap是X的像矩阵，因此对YFastMap进行PCA，其结果YiFastMap等于CMDS坐标。

基于上述讨论，文献[17]提出了iFastMap算法。首先确定一个内在维数等于m的样本子集（称之为枢轴子集），然后在这个子集上确定m个枢轴，将各样本投影到这些枢轴上，最后对投影结果进行PCA。

算法2iFastMap算法

输入：距离矩阵D=(dij),内在维数m。

输出：iFastMap坐标。

1.利用子集选择算法确定n,取前n个样本构成枢轴子集；

2.在这个样本子集上运行FastMap算法

2.1初始化

令k=0；，i,j∈{1,2,…,n}

2.2重复以下投影过程m次；

2.2.1k=k+1；

3.对枢轴子集以外的样本执行以下操作

3.1k=0；

3.2重复以下投影过程m次；

3.2.1k=k+1；

3.2.3利用式（8）计算i与{1,2,…,n}中样本点之间的距离；

4.对YFastMap进行主成分分析，返回其结果YiFastMap。

由于每次投影只需计算各点与枢轴点之间的距离，当m≪N时，iFastMap算法的运算时间为Θ(m2N)，它具有线性时间复杂度。

3.2　dcMDS算法

在iFastMap算法中，选定的子集与样本上其他所有点的距离必须已知。但在实际应用中，经常出现只知道局部距离信息的情形。下面讨论如何基于局部信息求出整个样本集的CMDS坐标。

每个局部对应一个样本子集。根据前面的讨论，如果对每个子集直接用CMDS求解，会得到各子集原始坐标矩阵在不同保距变换下的像矩阵。因此，必须将这些像矩阵整合成同一保距变换下的像矩阵。

首先考虑两个样本子集的整合。假定子集A在下的像矩阵为YA，子集B在下的像矩阵为ZB。A、B的像矩阵能够整合的前提是二者之间存在一个内在维数等于m的交集，用C表示。根据文献[18]，C在、下的像矩阵YC、ZC之间存在保距变换，满足：

其中，NC表示C中样本个数。因为C的内在维数等于m，所以可以利用线性回归求出。

文献[18]进一步指出，如果将作用于YA，有：

这表明，利用，把A在保距变换下的像矩阵YA转换成在下的像矩阵，使得A与B具有相同的保距变换，即A向B“对齐”。

对多个子集的情形：首先，从每个子集中随机抽取部分点，构成一个内在维数等于m的“基准”子集；然后，将各个“基准”子集合并成一个“基准”集，并求出“基准”集的CMDS坐标；最后，将各子集向“基准”集“对齐”。

在像矩阵对齐的基础上，结合分而治之策略[22-23]，作者提出了dcMDS算法[18]。dcMDS算法包含两个过程：首先将样本集自上而下逐级划分，即将样本集分成若干子集，如果子集的规模仍很大，则将子集进一步划分，直到每个子集足够小。第二个过程是自下而上逐级求子集的解。最底层的子集采用CMDS直接求解；底层子集的解逐级整合，直到得到整个样本集的像矩阵。根据定理1，对该像矩阵进行PCA，其结果YdcMDS与CMDS坐标完全一致。

根据文献[18]，当m≪N时，dcMDS的运算时间为Θ(NlgN)。

3.3　iLMDS算法

在LMDS中，首先选取部分点作为标志点，然后计算标志点的CMDS坐标，最后给出其余点的欧氏坐标。LMDS算法归纳如下。

算法3LMDS算法

输入：距离矩阵D=(dij),内在维数m。

输出：LMDS坐标。

1.不失一般性，取前n个点作为标志点；

2.利用式（2）求标志点的中心化内积矩阵Bn；

令m1=rank(Bn)，则Bn有m1个正特征值对应的单位正交特征向量为

3.计算LMDS坐标：

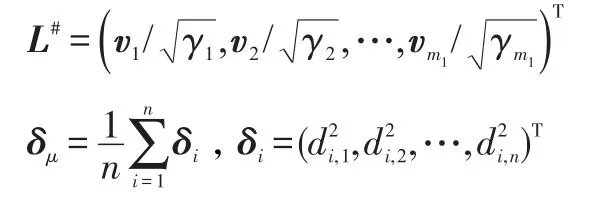
由于将特征值的计算仅限于标志点，而在计算各点坐标时采用的是线性公式，当m≪N时，LMDS具有线性时间复杂度Θ(N)。

根据文献[15]，LMDS坐标是各样本在标志点主轴向量上的投影，即：

从上式可以看出，如果m1=m，YLMDS是X的像矩阵。根据定理1，只需对YLMDS进行PCA，其结果YiLMDS等于CMDS坐标。

在LMDS算法中，对标志点的选取，只强调了n至少取为m+1，这不能确保m1=m。其实，只需采用子集选择算法，就可以确保标志点集的内在维数等于m，从而得到CMDS的一致解。

基于上述分析，本文提出iLMDS算法，它由以下步骤组成：

（1）利用子集选择算法确定n值，采用前n个样本构成标志点集；

（2）调用LMDS算法求样本集的CMDS坐标矩阵YLMDS；

（3）对YLMDS进行PCA，其结果YiLMDS等于样本集的CMDS坐标，即：

4　实验

实验采用Acer TM4330笔记本电脑，CPU为双核1.6 GHz，内存为2 GB；采用Matlab 2010a编程。针对USPS[24]和UCI[25]上的多组数据进行了实验。原始数据对应样本的各种属性，换句话说，它们都属于原始坐标，因此实验之前，先把它们转换成样本间的欧氏距离。每个实验都与CMDS算法进行对比，而CMDS算法对计算机的CPU、内存要求都很高，因此对于数据规模超过4 000的数据，都只选择其前4 000个样本。第1个实验针对一组基准数据集比较了快速多维标度算法解与CMDS解的差异；第2个实验比较了它们在该基准数据集上的运算时间；第3个实验研究了它们的运算时间随样本个数的变化规律。

4.1　快速多维标度算法与CMDS算法解的一致性

为了验证快速算法与CMDS算法解的一致性，本文采用以下两个指标衡量快速算法与CMDS算法结果的差异。

（1）“标准化”误差

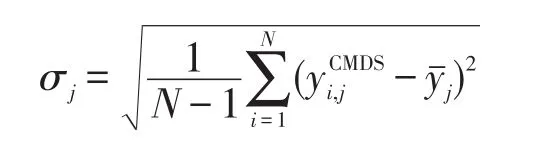
（2）stress值

下式定义的stress[26]值常用来衡量多维标度算法的性能。

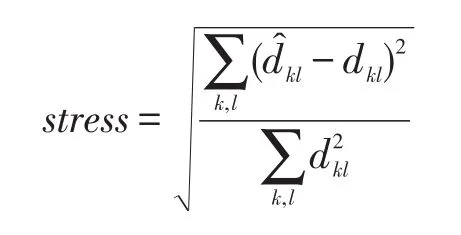
其中，̂kl表示依据某快速算法坐标得到的欧氏距离；dkl表示依据CMDS坐标得到的欧氏距离。stress值衡量了这两种距离的差，并用CMDS距离的和进行归一化。

从表2、表3中可以看出，各种快速算法的“标准化”误差和stress值都几乎为0，表明快速算法能得到与CMDS算法一致的解。

Table 2　Normalized error of algorithms表2　各种算法的“标准化”误差

Table 3　stressof algorithms表3　各种算法的stress值

4.2　各种算法的时间

Table 4　Running time of algorithms表4　各种算法的运算时间

各种算法的运算时间如表4所示。可以看出，3种快速算法在速度上都有了明显改善。对大多数样本集，它们的时间都在1 s以内。对usps这样的数据集，由于样本间的相关性较强，计算标志点集（枢轴点集）的时间增大，影响了速度，但即便如此，它们仍比CMDS算法快。

4.3　运算时间与样本个数的关系

为了定量分析各种算法运算时间与样本个数的关系，本文利用Matlab生成40组20维的随机数，各组随机数的个数为N=100,200,…,4 000。各算法的运算时间如图1所示。从图中可以看出，3种快速算法的速度较CMDS有了很大的提高。

Fig.1　Time of algorithms vs.number of samples图1　各种算法运算时间与样本个数的关系

进一步的分析表明：CMDS的运算时间在2.5×10-8×N3和 9.2×10-9×N3之间；iLMDS在N/140 000和N/240 000之间；iFastMap在N20 000和N/35 000之间；dcMDS在2.5×10-5×NlgN和1.5×10-5×NlgN之间。实验结果验证了前面的分析，即CMDS、iLMDS、iFastMap、dcMDS的时间复杂度分别为Θ(N3)、Θ(N)、Θ(N)、Θ(NlgN)。

5　讨论

本文回顾了iFastMap和dcMDS算法，并提出了iLMDS算法。与CMDS算法不同的是，它们都是将样本投影到一个子集上，从而提高了速度。

下面首先对比这3种算法的特点，然后讨论各种算法中子集的选择。

（1）3种算法的特点分析

在CMDS实际问题中，样本集的距离信息可能以多种方式呈现，如图2所示。图（a）各样本间的距离已知；图（b）存在一个特殊的子集，该子集与样本集上各点的距离已知；图（c）只知道相邻样本之间的距离。

Fig.2　Three kinds of given distances图2　3种距离情形

显然，CMDS算法只能求解第一种情形；iLMDS和iFastMap算法可用于前两种情形；dcMDS算法可用于任何一种情形。由此可见，快速算法拓展了多维标度算法的应用领域。

另外，CMDS是一种“批量”算法，即如果样本集新增了样本，必须重新计算，才能得到各点的坐标；而iFastMap和iLMDS都属于“增量”式算法，可以在求出标志点集（枢轴子集）后，逐一计算新样本的坐标。dcMDS算法也可以通过整合计算新样本的坐标。

（2）子集的选择

快速算法都涉及子集的选择。确定iFastMap中的枢轴子集、iLMDS中的标志点集以及dcMDS中各“基准”子集，其判断准则都是一样的，即它们的内在维数等于m。

如前所述，在dcMDS算法中，对样本集采取自上而下逐级划分，直至每个子集足够小。在实际应用中，对规模小于4m的子集停止划分，以确保从该子集中能抽取出内在维数等于m的“基准”子集。

对枢轴子集、标志点集以及“基准”子集的抽取，都采用子集选择算法。表5列出了这些子集的n值，其中dcMDS给出的是所有“基准”子集的最大n值。

从表5中可以看出，对多数样本集，随机选取m+1个样本所得到的样本子集，其内在维数等于m。

（3）未来的工作

CMDS是一种常用的数据降维和可视化方法，应用领域非常广泛。本文侧重阐述3种快速算法的基本理论，从理论上阐明它们与CMDS解的一致性。为了验证它们的高效性以及与CMDS解的一致性，所有的实验都与CMDS算法进行对比，这限制了实验中样本集的规模。将这些算法应用于大数据，是下一阶段的工作。

Table 5　Size of chosen subsets表5　各算法选取的子集大小

6　结束语

本文提出了一种新的快速多维标度算法，并介绍了原来提出的另两种快速多维标度算法。这3种方法都能得到与CMDS一致的解，而在速度上较CMDS有很大提高。下一阶段的工作是考虑将这些算法用于解决数据降维和可视化问题。

[1]Mayer-Schönberger V,Cukier K.Big data:a revolution that will transform how we live,work,and think[M].New York:Houghton Mifflin Harcourt,2013:6-15.

[2]Verleysen M,François D.The curse of dimensionality in data mining and time series prediction[C]//LNCS 3512:Proceedings of the 8th International Work-Conference on Artificial Neural Networks,Barcelona,Jun 8-10,2005.Berlin,Heidelberg:Springer,2005:758-770.

[3]Cox T F,Cox Michael A A.Multidimensional scaling[M].Boca Raton:Chapman&Hall/CRC,2001:38-44.

[4]Wu Chunqing,Ren Peige,Wang Xiaofeng.Survey on semanticbased organization and search technologies for network big data[J].Chinese Journal of Computers,2015,38(1):1-17.

[5]Ingram S,Munzner T.Dimensionality reduction for documents with nearest neighbor queries[J].Neurocomputing,2015,150(1):557-569.

[6]Patel A P,Tirosh I,Trombetta J J,et al.Single-cell RNA-seq highlights intratumoral heterogeneity in primary glioblastoma[J].Science,2014,344(6190):1396-1401.

[7]Wang Shaowei,Zhuo Zhizheng,Yang Hongyu,et al.An approach to facial expression recognition integrating radial basis function kernel and multidimensional scaling analysis[J].Soft Computing,2014,18(7):1363-1371.

[8]Vogelstein J T,Park Y,Ohyama T,et al.Discovery of brainwide neural-behavioral maps via multiscale unsupervised structure learning[J].Science,2014,344(6182):386-392.

[9]Chalmers M.Alinear iteration time layout algorithm for visualising high-dimensional data[C]//Proceedings of the 7th IEEE Visualization Conference,San Francisco,Oct 27-Nov 1,1996.Piscataway:IEEE,1996:127-131.

[10]Morrison A,Ross G,Chalmers M.Fast multidimensional scaling through sampling,springs and interpolation[J].Information Visualization,2003,2(1):68-77.

[11]Williams M,Munzner T.Steerable,progressive multidimensional scaling[C]//Proceedings of the 10th IEEE Symposium on Information Visualization,Austin,Oct 10-12,2004.Washington:IEEE Computer Society,2004:57-64.

[12]Faloutsos C,Lin K.FastMap:a fast algorithm for indexing,data-mining and visualization of traditional and multimedia datasets[C]//Proceedings of the 1995 ACM SIGMOD International Conference on Management of Data,San Jose,May 22-25,1995.New York:ACM,1995:163-174.

[13]An Jiyuan,Yu J X,Ratanamahatana C A,et al.A dimensionality reduction algorithm and its application for interactive visualization[J].Journal of Visual Languages&Computing,2007,18(1):48-70.

[14]Wang J T L,Wang Xiong,Shasha D,et al.MetricMap:an embedding technique for processing distance-based queries in metric spaces[J].IEEE Transactions on Systems,Man,and Cybernetics:Part B Cybernetics,2005,35(5):973-987.

[15]de Silva V,Tenenbaum J B.Sparse multidimensional scaling using landmark points[R].Palo Alto:Stanford University,2004.

[16]Platt J C.FastMap,MetricMap,and Landmark MDS are all Nyström algorithms[C]//Proceedings of the 10th International Workshop on Artificial Intelligence and Statistics,Bridgetown,Jan 6-8,2005:261-268.

[17]Qu Taiguo,Cai Zixing.An improved FastMap algorithm[J].Journal of Nanjing University:Natural Sciences,2016,52(4):682-692.

[18]Qu Taiguo,Cai Zixing.A divide-and-conquer based multidimensional scaling algorithm[J].Pattern Recognition andArtificial Intelligence,2014,27(11):961-969.

[19]Zhang Runchu.Multivariate statistical analysis[M].Beijing:Science Press,2006.

[20]You Chengye.Analytic geometry[M].Beijing:Peking University Press,2004.

[21]Young G,Householder A S.Discussion of a set of points in terms of their mutual distances[J].Psychometrika,1938,3(1):19-22.

[22]Tian Wenbiao,Rui Guosheng,Kang Jian.Divide and conquer method for sparsity estimation within compressed sensing framework[J].Electronics Letters,2014,50(9):677-678.

[23]Li Shengguo,Gu Ming,Cheng Lizhi,et al.An accelerated divide-and-conquer algorithm for the bidiagonal SVD problem[J].SIAM Journal on Matrix Analysis and Applications,2014,35(3):1038-1057.

[24]Hull J J.A database for handwritten text recognition research[J].IEEE Transactions on Pattern Analysis and Machine Intelligence,1994,16(5):550-554.

[25]Lichman M.UCI machine learning repository[EB/OL].(2013).[2016-05-03].http://archive.ics.uci.edu/ml.

[26]Kruskal J B.Nonmetric multidimensional scaling:a numerical method[J].Psychometrika,1964,29(2):115-129.

附中文参考文献：

[4]吴纯青,任沛阁,王小峰.基于语义的网络大数据组织与搜索[J].计算机学报,2015,38(1):1-17.

[17]屈太国,蔡自兴.一种改进的FastMap算法[J].南京大学学报:自然科学,2016,52(4):682-692.

[18]屈太国,蔡自兴.基于分而治之的多维标度算法[J].模式识别与人工智能,2014,27(11):961-969.

[19]张润楚.多元统计分析[M].北京:科学出版社,2006.

[20]尤承业.解析几何[M].北京:北京大学出版社,2004.