度相关性对复杂网络目标控制的影响*

仇智鹏，鲁富荣，杜亚星，钱宇华+

1.山西大学 大数据科学与产业研究院，太原 030006

2.山西大学 计算智能与中文信息处理教育部重点实验室，太原 030006

3.山西大学 计算机与信息技术学院，太原 030006

1　引言

随着对复杂网络的深入研究，复杂网络的结构、演化以及动力学问题已经获得许多重要的突破[1-4]。对于复杂网络动力学性质的研究，其最终目标是如何控制一个网络以达到期待的目标状态。复杂网络的可控性问题是近年来提出的重要研究热点之一。复杂网络控制方面主要的工作包括牵制控制[5-6]和结构控制[3,7]等。近期的工作主要包括复杂网络的可观测性[8]、目标可控性[9]、控制能量[10]、精确可控性[11]及多层网络的结构和动力学性质[12]等方面的研究[13-19]。对于复杂网络而言，控制的目的是如何通过恰当的输入在有限时间内使得网络在自身动力学机制下演化到任意想要的状态[20-21]。2011年，Liu等人[3]通过将复杂网络的完全可控问题转化为图论中的最大匹配问题，找到了控制网络的最少驱动节点数。2013年，Yuan等人[11]基于可控性的PBH秩判据提出了对于复杂网络的精确控制，从而简化了对于无向复杂网络驱动节点数的计算。然而，对于真实网络而言，对整个网络进行完全控制有时是费时费力的，甚至是不可行的，例如微生物网络和一些社会网络，它们规模庞大且结构复杂。出于这个考虑，Gao等人[9]基于结构控制理论，利用贪婪算法提出了对网络的目标控制。该算法首先选择一部分节点作为需要控制的目标节点，再通过迭代使用匹配算法最终找到了驱动该部分目标节点达到理想状态的最小驱动节点及其数目。

度相关性[22]是刻画网络属性的一个重要指标，反映节点与其相邻节点之间度的联系。本文考虑的是有向网络的度相关性，具体为入度-入度相关性、入度-出度相关性、出度-入度相关性、出度-出度相关性。如果网络中两个节点的边连接情况与两个节点的度值无关，称网络不具有度相关性。如果度值较大的节点倾向于连接度值较大的节点，那么就称这个网络是同配的。反之，如果度值较大的节点倾向于连接度值相对较低的节点，那么就称这个网络是异配的。

由于复杂网络节点数目多，连边复杂度高，不能像低维小系统一样通过遍历的方法来寻找控制输入位置。因此，如何有效地确定所需要独立控制的节点数目和控制输入的位置，以满足复杂网络可控性的要求就成为网络控制需要解决的首要问题。对于控制而言，除了探究其控制的机理，提出有效的控制手段之外，探究影响该控制方法效率的因素也是一个重要的方面。度相关性对于复杂网络结构可控具有重要的影响已经被证实[23]。在真实网络中，例如电力网络、生物网络，其度相关性呈现出一定的异配性，而社会网络呈现出一定的同配性，网络的同配性与异配性会影响这些网络控制的效率。而目标控制是采用贪婪算法，在结构控制的基础上实现对于网络部分节点的控制，因此本文选取度相关性作为目标控制的影响因素进行研究。探究复杂网络目标控制的影响因素，能够更好地认识网络的拓扑结构对于网络目标控制的影响，同时也能够在此基础上改进网络使得网络更易于被目标控制。

本文探究了各种度相关性对于目标控制效率的影响。实验结果表明在目标控制的机制下，出度-入度相关性对网络的目标控制效率影响较大，而随着出度-入度相关性的逐步增加，驱动节点比例呈逐步下降趋势。

2　相关内容

2.1　目标控制

本文采用的目标控制策略是由Gao等人[9]提出的，研究的是线性时不变系统的目标控制：

其中，x∈RN,u∈RM,y∈RS，这3个变量分别代表了系统的状态向量、输入向量以及输出向量。A∈RN×N，B∈RN×M，C∈RS×N，分别表示状态矩阵、输入矩阵以及输出矩阵。A描述的是系统的线性连接关系；B决定了外部输入信号与网络节点之间的连接关系；u是随时间变化的输入信号；C是所需要控制的目标节点。对于一个具有N个节点的网络N={1,2,…,N}，所需要控制的目标节点集合是C={c1,c2,…,cS}，其中，S=|C|=fN。表示输出的矩阵C=[I(c1),I(c2),…,I(cS)]，其中I(i)表示一个N×N单位矩阵的第i行。如果给定一个时变的输入向量u(t)=(u1(t),u2(t),…,uM(t))T，这样一个输入向量可以使得目标节点变成任意期望的最终状态，那么就说这个系统是目标可控的。目标控制可以被看作一种（A,B,C）特殊的输出可控，而且在满足如下条件的情况下：

如果满足（2），对于任意的初始状态x(0)，就可以计算出最优化的输入向量u(t)使得网络可以在有限时间tˉ>0达到任意最终状态yˉ，也就是说最终y(tˉ)≡yˉ。

为了解决目标控制问题，采用“K-walk theory”。该理论的原理是：一个节点可以控制这样的一组目标节点，即从驱动节点到任意目标节点的路径长度是互不相同的。使用“K-walk theory”就可以确定这样的一个受控节点的集合。对于需要超过一个控制输入的网络，采用贪婪算法（图1），来找到最少的输入节点。图1（a）中对一个小型网络施加目标控制。网络中一共7个节点，其中节点{x3,x4,x6,x7}为目标节点（红圈标出）。在图1（b）中使用贪婪算法来解决网络的目标控制问题。首先，将原网络映射成一个二分图的形式。目标节点是{x3,x4,x6,x7}，通过红线所示的第一次迭代之后，找到匹配节点{x2,x3,x5,x6}，将这些节点作为第二次迭代的目标节点。通过3次迭代，最终得出{x1,x5}是{x3,x4,x6,x7}的驱动节点。

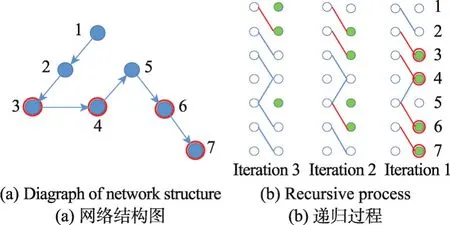
Fig.1　Progress of target control图1　目标控制过程

2.2　度相关性

度相关性可以度量节点之间的连接趋势，而且它可以有多种表示形式。本文采用皮尔逊相关系数刻画度相关性：

2.3　度相关性影响

本文所研究的是度相关性对于网络目标控制的影响。如图2所示，从一个简单的角度考虑一个网络。在图2（a）中，该矩阵为随机重连之前网络的连接矩阵，左半部分代表源节点（即有向边的出节点），右半部分代表终节点（即有向边的指入点）中N=7。图2（b）展示的是随机重连之后网络的连接矩阵。

Fig.2　Connection matrix of networks before and after change图2　网络重连前后的连接矩阵

Fig.3　Effect of degree correlations on target control图3　度相关性对目标控制驱动节点的影响

在图3（a）～（d）中，所要控制的是{x3,x4,x6,x7}4个节点。图（a）是初始网络的连边图，图（b）通过目标控制算法找出的网络最终驱动节点{x1,x5}，图（c）是随机重连之后生成的网络连边图，图（d）为改变度相关性之后，通过目标控制算法找出的网络最终驱动节点变为{x5}，从而使得驱动节点的数目降低。因此，网络的目标可控性会受到度相关性的影响。

3　度相关性影响的实验分析

3.1　模拟退火算法

为了探索度相关性对于复杂网络目标控制的影响，本文采用模拟退火算法，使得在保持度分布不变的情况下，改变度相关性到任意期望的目标值。

（1）设定了初始温度T和每个温度下的迭代次数iter，以及能量函数E(r)=|r-r*|；

（2）采用随机扰动的方法，每次从网络中任取两条边，交换两条连边的终节点，该操作的目的是使得网络中每个节点的出度和入度保持不变；

（3）计算出E(r)的值，看是否小于阈值，如果小于阈值，则已经达到所需要的r值范围；

（4）继续迭代，直到达到所需要的r值范围，或者温度T小于所设定的最小温度t。

3.2　度相关性对E-R随机网络的实验分析

图4为在E-R随机网络中度相关性对目标控制的影响(nD=ND/(N×p))。其中，nD为目标控制驱动节点比例，ND为驱动节点数目，N为节点数，p为选择的目标节点比例。本文研究的是度相关性对网络目标控制的影响，因此每次随机选取一半的节点(p=50%)为目标节点。该E-R随机网络的平均度为=1(red),=2(green),=3(blue),=5(black)。图中每一个数据点为5次实验取平均值。图4（a）考虑了入度-入度相关性(rin-in)和驱动节点比例(nD)的关系；图4（b）考虑了入度-出度相关性(rin-out)和驱动节点比例(nD)的关系；图4（c）考虑了出度-入度相关性(rout-in)和驱动节点比例(nD)的关系；图4（d）考虑了出度-出度相关性(rout-out)和驱动节点比例(nD)的关系。

实验表明对于目标控制而言，在4种度相关性中，出度-入度相关性的影响最为明显。

对于E-R随机网络，首先从入度-入度相关性角度来看，在网络处于异配的情况(rin-in<0)，网络中入度较大的节点连接网络中入度较小的节点，而该入度较小的节点连接网络中入度较大的节点。从形成匹配的角度来看，该结构会在形成二阶路径的过程中，浪费大量的入边，从而抑制了网络中其他匹配的形成，加大了网络目标可控的难度。

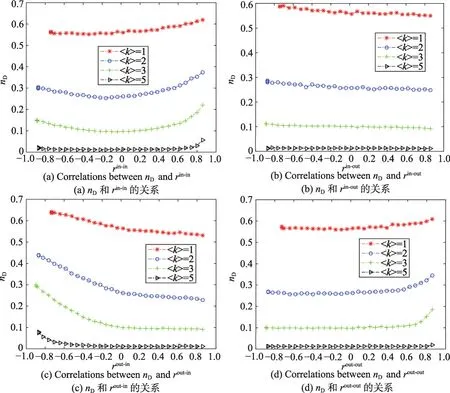
Fig.4　Correlations betweennDand all kinds ofrin random network图4　随机网络中驱动节点比例和各种相关性的关系

因此，网络异配性较强(r<-0.3)时，网络的驱动节点比例较大。通过模拟退火算法改变网络的度相关性后，网络在逐步变为同质网络(rin-in>0)的过程中，相关性逐步上升，由二阶路径所带来的对于匹配的抑制性降低，所以网络驱动节点的比例逐步下降。而当网络的入度-入度相关性逐步增加时，网络中入度较高的节点相互连接，使得网络中入边存在较大的浪费，所以在度相关性增高的后半阶段，目标控制的驱动节点比例逐步上升。因此，随着网络入度-入度相关性的增加，网络的驱动节点比例首先会逐步降低，在网络入度-入度相关性增高的后半阶段，网络驱动节点比例逐步上升。

从入度-出度相关性的角度来看，在求网络中目标节点的驱动时，所考虑的是节点之间的匹配关系。以连边两端的节点考虑，对于源节点而言，考虑的是源节点的出度，而对于连边另一端的节点，考虑的是其入度，以此衡量网络中的匹配数目。这样的一个匹配数目与网络的入度-出度相关性几乎无关，因此网络的目标可控性对于网络的入度-出度相关性没有体现出很强的依赖关系。

从出度-入度相关性的角度来看，因为有向网络的控制问题可以转化为匹配问题，而匹配本身从源节点的角度看就是出边，从终节点的角度看就是入边，所以网络本身体现出对于该相关性很高的依赖性。当网络体现出很高的异配性时（网络中节点的出度很高而入度很低时），因为该出度高的节点只能控制其中一个入度低的节点，所以想要控制其他入度低的节点就需要另外施加控制输入，网络的异配性对于网络的目标可控体现出较高的抑制性。因此，对于目标控制而言，其驱动节点的比例会相对较高。反之，如果网络有良好的同配性，则对于出度较低的节点，其入度也会较低，对于网络中出边或者入边的利用率较高，在形成匹配的过程中，目标节点易处于一条有向路径中。因此，当网络同配性越来越高时，网络的驱动节点比例会降低。

对于出度-出度相关性而言，网络驱动节点的比例体现出和入度-入度相关性良好的吻合。因为如果将原网络中所有的连边反向，则网络中的匹配性质不会发生变化，即网络的驱动节点比例不会发生变化，此时网络的出度-出度相关性等价于原来的入度-入度相关性，所以网络的驱动节点比例与入度-入度相关性图所体现出来的规律一致。

3.3　度相关性对S-F无标度网络的实验分析

如图5所示，对于该无标度网络，其平均度=1,=2,=3,=5,γ=3,N=5 000。目标节点的选择也是每次随机选择总节点数目的一半(p=50%)。每一个数据点都是取了5次实验的平均值。图5表示了驱动节点比例和4种度相关性之间的关系。对于S-F无标度网络而言，度相关性对于其影响表现出和E-R随机网络类似的性质。

Fig.5　Correlations betweennDand all kinds ofrin scale-free network图5　无标度网络中驱动节点比例和各种相关性的关系

从入度-入度相关性和出度-出度相关性的角度来看，在目标控制中，所体现的性质与E-R随机网络相差不大。然而，因为网络为S-F无标度网络，不考虑网络中具体连边的方向，网络本身体现出较高的异配性，即使网络的入度-入度相关性逐步增加，网络本身也很难有较高的同配性，所以不容易构成入度-入度相关性对于网络形成匹配的抑制，从而网络在入度-入度相关性由-1到+1的过程中都保持驱动节点比例逐步降低。而当网络的入度-入度相关性极高时，网络中入度较高的节点相互连接，使得网络中入边存在较大的浪费，所以在度相关性接近+1的时候，目标控制的驱动节点比例存在上升的趋势。因此，随着网络入度-入度相关性的增加，网络的驱动节点比例首先会逐步降低，在网络入度-入度相关性极高时，网络驱动节点比例存在逐步上升的趋势。

从入度-出度和出度-入度相关性的角度来看，入度-出度相关性对于网络目标控制驱动节点比例几乎没有影响，而出度-入度相关性对S-F无标度网络影响较大，且随着出度-入度相关性的增加，驱动节点比例逐步降低。

3.4　真实网络

本节用真实网络数据检验相关性对于网络目标控制效率的影响。所用的真实网络的部分数据如表1所示，表格内从左到右的内容依次为真实网络的编号、类型、名字、节点数目以及连边数目。

Table 1　Data of real networks表1　真实网络的数据

一共考虑了7个真实网络，依旧随机选择总节点的一半节点(p=50%)作为目标节点，其中每个数据点重复5次实验取平均值，所得出的关系如图6所示。

对于选取的TRN-EC-Alon、TRN-EC-RDB64、TRNYeast-Alon而言，入度-入度相关性整体变化趋势不明显，但是在度相关性极高时驱动节点比例是增高的。而入度-出度相关性在该类型网络上几乎没有影响。出度-入度相关性对于网络驱动节点的比例影响较为明显，随着相关性的逐步增加，网络的驱动节点比例逐步减少。由于真实网络的限制，网络在出度-出度相关性上无法有很大范围的变化，然而在小范围内的变化是伴随度相关性的增加先降低后增高。

对于S420、S838网络而言，从入度-入度的角度看，在度相关性为负时网络的驱动节点比例浮动不大，而当度相关性取正值的时候网络的驱动节点比例随度相关性的增加而逐步上升。入度-出度相关性对于网络驱动节点比例的影响不大。而伴随网络出度-入度相关性的增加，网络的驱动节点比例迅速下降，对于出度-出度相关性而言，网络体现出和入度-入度相关性良好的匹配，在负值时网络的驱动节点比例变化不大，当网络度相关性逐步变为+1的过程中，网络驱动节点的比例逐步上升。

对于Dolphins、Prisoninmate网络而言，伴随着网络入度-入度相关性的增加，网络的驱动节点比例先是逐步下降，然后逐步上升。入度-出度相关性对其几乎没有影响，伴随着出度-入度相关性的增加，网络的驱动节点比例逐步降低。出度-出度相关性与入度-入度相关性的表现几乎一致。

4　结论

通过对E-R随机网络、S-F无标度网络和真实网络的实验数据分析，本文最终能得出各种度相关性对网络目标控制效率影响的结论。

（1）对于绝大部分网络而言，在入度-入度相关性由-1变为+1的过程中，网络的驱动节点比例先是逐步降低，在度相关性为0的附近，网络的驱动节点比例取得最低，并且在度相关性很小范围内几乎保持不变。随后，当网络的度相关性增大，网络的驱动节点比例也随之上升。

（2）入度-入度相关性，对于网络目标控制的驱动节点比例几乎没有影响。

（3）出度-入度相关性，伴随着出度-入度相关性的增大，网络的驱动节点比例逐步降低，且该相关性对于网络驱动节点比例的影响最大。

（4）出度-出度相关性，该相关性对于网络目标控制驱动节点的比例影响与入度-入度相关性几乎一致，都是随着网络度相关性的增大，驱动节点比例先降低后升高。

Fig.6　Correlations betweennDand all kinds ofrin real networks图6　真实网络中驱动节点比例和各种相关性的关系

5　展望

本文研究了在复杂网络中，4种度相关性对于目标控制的影响，其中网络的出度-入度相关性对于网络的目标可控性具有较强的影响，并揭示了对于复杂网络目标控制的影响因素，及其带来的一些问题。接下来的研究方向主要包括：如何通过调整网络的结构使得在目标控制的情况下，网络的驱动节点数目尽可能得少；探究各种度相关性影响的内在机理；对于真实网络，如何调整才能使其更易被控制等。

[1]Newman M,BarabásiAL,Watts D J.The structure and dynamics of networks[M].Princeton:Princeton University Press,2011.

[2]Boccaletti S,Latora V,Moreno Y,et al.Complex networks:structure and dynamics[J].Physics Reports,2006,424(4):175-308.

[3]Liu Yangyu,Slotine J J E,Barabási A L,et al.Controllability of complex networks[J].Nature,2011,473(7346):167-173.

[4]Barabási A L,Albert R.Emergence of scaling in random networks[J].Science,1999,286(5439):509-512.

[5]Wang Xiaofan,Chen Guanrong.Pinning control of scale-free dynamical networks[J].Physica A:Statistical Mechanics and itsApplications,2002,310(3):521-531.

[6]Manaffam S,Seyedi A.Pinning control for complex networks of linearly coupled oscillators[C]//Proceedings of the 2013 American Control Conference,Washington,Jun 17-19,2013.Piscataway:IEEE,2013:6364-6369.

[7]Cowan N J,Chastain E,Vilhena D A,et al.Nodal dynamics,not degree distributions,determine the structural controllability of complex networks[J].PLOS ONE,2011,7(6):e38398.

[8]Liu Yangyu,Slotine J E,Barabási A L,et al.Observability of complex systems[J].Proceedings of the National Academy of Sciences of the United States of America,2013,110(7):2460-2465.

[9]Gao Jianxi,Liu Yangyu,D'Souza R M,et al.Target control of complex networks[J].Nature Communications,2014,5:5415.

[10]Yan Gang,Ren Jie,Lai Yingcheng,et al.Controlling complex networks:how much energy is needed?[J].Physical Review Letters,2012,108(21):218703.

[11]Yuan Zhengzhong,Zhao Chen,Di Zengru,et al.Exact controllability of complex networks[J].Nature Communications,2013,4:2447.

[12]Boccaletti S,Bianconi G,Criado R,et al.The structure and dynamics of multilayer networks[J].Physics Reports,2014,544(1):1-122.

[13]Gao Jianxi,Barzel B,Barabási A L.Universal resilience patterns in complex networks[J].Nature,2016,530(7615):307-312.

[14]Buldyrev S V,Parshani R,Paul G,et al.Catastrophic cascade of failures in interdependent networks[J].Nature,2010,464(7291):1025-1028.

[15]Liu Xueming,Stanley H E,Gao Jianxi,et al.Breakdown of interdependent directed networks[J].Proceedings of the National Academy of Sciences of the United States of America,2016,113(5):1138-1143.

[16]Zhang Xiyun,Boccaletti S,Guan Shuguang,et al.Explosive synchronization in adaptive and multilayer networks[J].Physical Review Letters,2014,114(3):038701.

[17]Menichetti G,Dall'Asta L,Bianconi G,et al.Network controllability is determined by the density of low in-degree and out-degree nodes[J].Physical Review Letters,2014,113(7):078701.

[18]Dörfler F,Chertkov M,Bullo F,et al.Synchronization in complex oscillator networks and smart grids[J].Proceedings of the National Academy of Sciences of the United States ofAmerica,2013,110(6):2005-2010.

[19]Zhang Y,Garas A,Schweitzer F,et al.Value of peripheral nodes in controlling multilayer scale-free networks[J].Physical Review E,2016,93(1):012309.

[20]Slotine J J E,Li Weiping.Applied nonlinear control[M].Upper Saddle River:Prentice Hall,1991.

[21]Haussmann U.Linear systems and optimal control[J].Siam Review,2012,31(4):696-698.

[22]Foster J G,Foster D V,Grassberger P,et al.Edge direction and the structure of networks[J].Proceedings of the National Academy of Sciences of the United States of America,2010,107(24):10815-10820.

[23]Pósfai M,Liu Yangyu,Slotine J J E,et al.Effect of correlations on network controllability[J].Scientific Reports,2013,3:1067.