面向JAUMIN的并行AFT四面体网格生成*

郑　澎，方　维，徐　权，冷珏琳，熊　敏，于长华

1.中国工程物理研究院 计算机应用研究所，四川 绵阳 621900

2.北京应用物理与计算数学研究所，北京 100088

3.中国工程物理研究院 高性能数值模拟软件中心，北京 100088

1　引言

并行自适应非结构网格支撑软件框架JAUMIN[1]（J adaptive unstructured mesh applications infrastructure）是北京应用物理与计算数学研究所研制的面向拉格朗日、欧拉等有限元计算方法的应用软件编程框架，它提升了非结构网格并行应用软件的计算效率，降低了研制难度，并已在重大科学装置结构力学分析与优化设计、裂变能源等重大项目中得到应用。在这些应用中，网格生成是实现高保真数值模拟的重要步骤，它需要生成能精确刻画复杂几何区域的高质量和高精度网格，同时还需要网格生成、网格数据结构必须与求解程序的并行操作相容，因此并行网格生成是本文研究的重点。

在有限元计算中，四面体网格能很好地逼近模型边界且自动化生成的程度高，比较有代表性的串行四面体网格生成方法有AFT[2-3]（advancing front technique）方法和Delaunay方法[4-5]。但对于同一几何模型，非结构六面体网格虽能用更小规模的网格取得同样的计算精度，生成过程需要更少的内存，但针对任意复杂几何模型自动生成六面体网格十分困难，全自动化六面体方法的适用性还在逐步研究中[6-7]。因此，权衡利弊，对于高性能数值模拟计算来说，其运行在具有数千上万核的、有超大规模内存的高性能计算机上，采用较成熟的四面体网格生成方法，自动化程度高，能够快速响应计算需求，且超大规模的高质量四面体网格也能够提高计算精度。目前，基于AFT方法的广为应用的开源四面体网格生成工具包有Netgen、商业工具包VKI等，均是花费10～15年时间研发的串行工具，离人们的需求所缺乏的是并行化。

迄今为止，网格并行生成是一项紧密耦合计算几何、网格数据结构、负载平衡和网格分区的复杂技术，主要有两类实现途径：第一类是直接对网格生成算法进行并行化[8-10]；另一类是将几何模型分解为子区域后再进行网格生成，这种方法可复用串行网格生成算法。例如：非开源并行网格生成工具ParTGen[11]，其并行核数最多能到500核，远远不能满足万亿次以上规模计算的需求；ITAPS（interoperable technologies for advanced petascale simulations）[12]是美能源部SciDAC计划支持的面向千万亿次高性能计算的研究项目，目标在于研发高可用的网格、几何、场生成的工具，它联合了美国各大学和三大实验室的力量，在不断发展中。

本文重点讨论第二类方法的实现，在分区时，考虑要尽量减少通讯和达到负载平衡。在并行计算领域，串行的分区程序Metis[13]、Zoltan[14]和它们的并行版都被广泛使用，本文在并行策略中，利用这些分区工具进行粗网格的并行分区，为大规模网格并行生成打下了基础。

2　网格数据结构

非结构四面体网格并行生成工具的输入是Brep格式描述的几何区域，而输出则是直接对接JAUMIN的J网格文件描述格式。在程序内部，紧凑的网格数据结构为网格并行生成提供了支撑，在单个并行计算节点上，它采用了局部信息存储方式，四面体-几何顶点、三角面-四面体、三角面-几何顶点等多种邻接关系映射。其中，四面体-顶点邻接关系包含所有网格单元，而其余邻接关系只保存在几何体和分界面上的三角面的邻接信息（如图1所示）。在单个并行计算节点上，还有描述原始几何区域的几何模型。

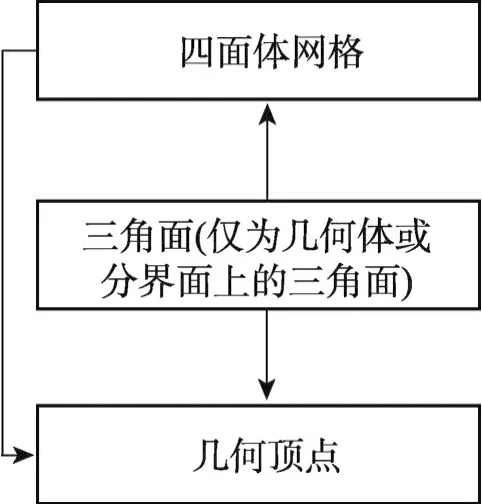
Fig.1　Mesh connected relations in memory图1　内存中的网格邻接关系

3　AFT并行四面体网格生成方法

3.1　并行策略

串行AFT四面体网格生成过程中，首先基于几何形状生成表面三角形网格，再从表面三角形网格出发生成体网格。考虑AFT网格生成算法并行化问题时，描述并发性的一种方式是将每个计算节点上的网格生成定义为一个任务，任务间仅有的共享数据是输入的模型，因为要访问的输入模型是只读的，所以任务间彼此独立，从而能够高效地使用任意合理数目的计算节点，节点间通信开销几乎为零。

为实现并行生成，本文采用先生成粗网格，再进行并行细化的方法，先后采用了两种并行策略。第一种策略如图2所示，首先直接针对Brep格式的输入模型进行划分，划分模型的方法采用KD-Tree方法，生成若干块子模型；然后按顺序给子模型生成表面网格，且各子模型块相邻面上的表面网格保持一致，将子表面网格分配到各计算节点，进行后续的体网格生成。

Fig.2　Parallel strategy by geometry partition method图2　基于几何分区方法的并行策略

这种方法并行效率高，可以将模型分成若干子模型，如图3所示。但几何计算不能达到负载均衡，且网格尺寸由初始尺寸决定，可扩展性不好。

Fig.3　Example of geometry partition图3　几何分割模型示意

第二种方法如图4所示，首先针对输入模型生成粗网格，然后采用串行的Metis或者Zoltan工具，根据粗网格的几何关联性进行分区，得到子区域网格（如图5所示），每个子区域网格具有几乎相同数量的节点和单元；接着将子区域网格分配到各计算节点，计算子区域的表面网格，不断重复网格精细化步骤，直到网格尺寸达到要求，再生成体网格。这种方法并行效率高，几何计算负载均衡性更好，能够不断精细化网格，可扩展性好。

Fig.4　Parallel strategy by coarse mesh partition method图4　基于粗网格分区方法的并行策略

Fig.5　Example of coarse mesh partition图5　粗网格分区示意

3.2　贴体加密

在本文采用的并行策略中，表面网格的精细化加密采用了贴体加密方法。

一般有代表性的表面网格细分加密方法有Loop[15]算法、Doo-Sabin算法、Catmull-clark算法和改进型的蝶形算法，这些算法都是通过逼近或者插值的方法对表面网格进行不断的光滑，并没有考虑表面网格所对应的输入模型的几何形状。

贴体加密方法示意如图6所示。其特点是对表面三角形网格进行边中点加密时，采用向分区模型的外表面进行投影的方法求得边中点P对应的加密点P′。

Fig.6　Surface mesh and after two times refinement图6　表面网格和一次、二次加密后的表面网格

由于表面三角形网格包括了输入模型的表面网格和分区产生的分界面网格，针对一个表面三角形单元的3个顶点的不同位置情况采用不同的加密点位置计算方法：当只有两个顶点位于输入模型表面网格时，且它们组成的边不为其他表面三角形单元共享时，用最短距离法求得加密点P′；当两个顶点位于分界面网格上，P′即为P；当两个顶点位于输入模型表面网格，一个顶点位于分界面网格时，采用法线方向的最短距离法求得加密点P′。由于加密原则一致，位于不同计算节点的相邻分界面上的网格保持一致。

3.3　表面网格的并行优化

采用Metis进行分区时，由于不会考虑天然几何外形的特点，会出现分区表面网格不够光滑和碎片化分区，如图7所示，最终影响生成的体网格的质量。

因此，对图4中的并行策略进行了改进，增加对分区表面网格进行优化的步骤，如图8所示，不断重复对分区表面网格进行优化和精细化加密的步骤，直到达到网格尺寸要求为止，进一步提高体网格的质量。由于对表面网格优化的步骤需要在计算节点间进行少量的通信，本文实际是借助JAUMIN框架建立了通信关系。

分区表面网格优化工作由本文作者和湘潭大学魏华祎老师小组共同完成，主要采用了节点优化算法，通过移动网格节点的坐标来改善节点周围三角形单元的形状。给定一节点Pi所在的单元片，如图9所示。

Fig.7　Coarse mesh of aircraft and fragmentations caused by partition图7　飞行器粗网格及分区造成的碎片区域

Fig.8　Adding optimization step to parallel strategy图8　并行策略中增加优化步骤

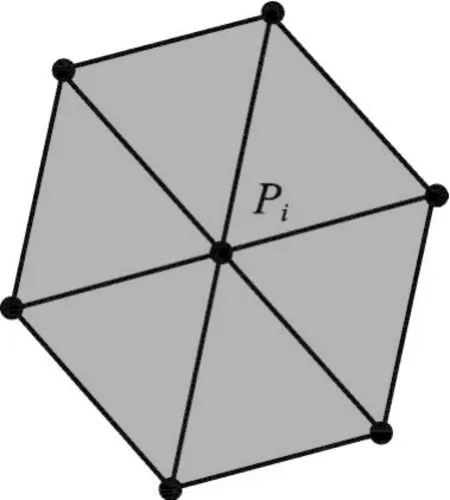
Fig.9　Triangular element图9　三角形单元片

节点优化算法实现了CPT、ODT和CVT共3种移点方法。

CPT方法采用Pi邻接单元的重心的平均来替代Pi坐标。设与Pi相邻单元的重心为bj，则：

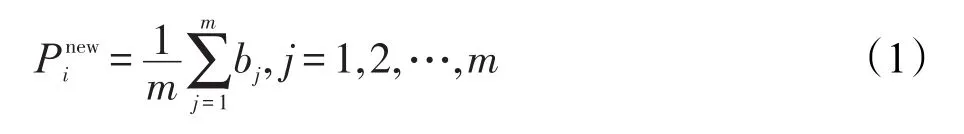
ODT方法是用Pi邻接单元的外接圆圆心的平均来替代Pi坐标。设与Pi相邻节点为Cj，则：

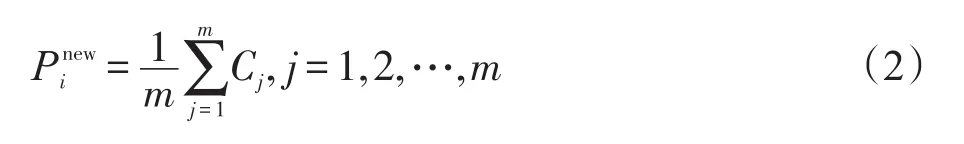
把Pi邻接单元的外接圆圆心依次连接起来，就会形成Pi的Voronoi区域Vi，用Vi的质心代替Pi，就是CVT方法，即：

节点移动过程中，移动方向可分解为沿曲面切线方向和法线方向的移动。其中，沿切线方向的移动改善单元的形状和尺寸，而沿法线方向的移动改善表面网格的光滑性。但为了保持输入模型的几何特征，对位于输入模型表面上的网格点要特殊处理，只能沿着输入模型的表面或特征曲线的切线方向移动，移动之后还必须采用3.2节提到的投影方法映射回模型表面。综合评价上述移点方法，CPT方法比较稳定，适应性更强，因为它是重心的平均，所以不会移出单元片之外，导致无效单元出现；CVT和ODT稳定性次之，但ODT的优化速度更快。

优化后的表面网格如图10所示。

Fig.10　Surface mesh and optimized surface mesh图10　表面网格和优化后的表面网格

表面网格优化方法解决了分区表面网格不够光滑的问题，但是对碎片化分区问题仍无法有效解决。

4　应用测试

基于本文的AFT四面体并行网格生成技术，在浪潮TS10K集群进行了同一基准模型的强可扩展测试，精细化加密次数均为2，该集群有64个计算节点，每个计算节点内存为64 GB。测试结果如表1和图11所示。

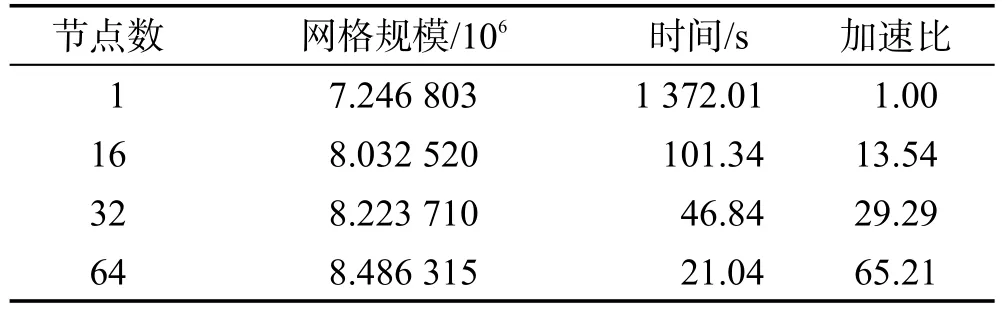
Table 1　ParallelAFT tetrahedral mesh generation test表1　并行AFT四面体网格生成测试

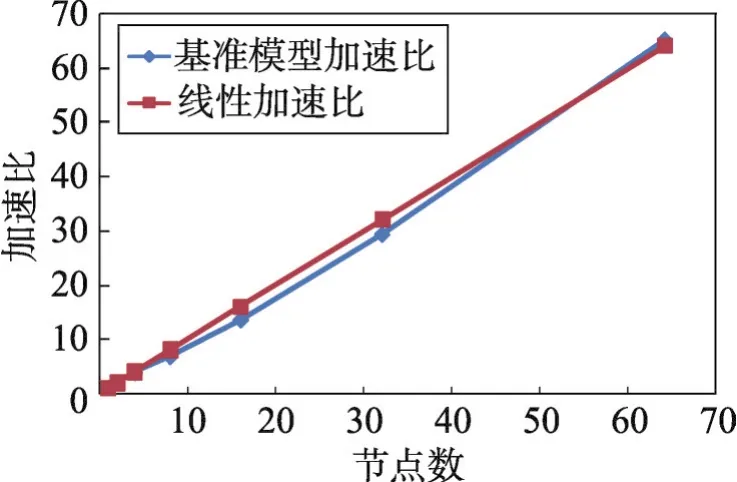
Fig.11　Strong extensible test图11　强可扩展测试

从图11中可看到几乎可以达到线性加速，具有良好的可扩展性，在64节点并行时，甚至出现了轻微的超线性。分析原因在于模型越复杂，在分区越多时，抽取表面网格的速度非线性提高，而模型不复杂时，则不会存在这一现象，说明该方法更适合复杂模型。本文利用该方法，在千万亿次高性能计算机上进行了实际应用，实现了针对神光III靶球装置的实际工程模型的高精度四面体网格生成，达到在1 min内8 192核并行生成2.2亿自由度网格，如图12所示。

Fig.12　Shengguang III target ball device and local details of mesh generation图12　神光III靶球装置和生成网格的局部细节

5　结束语

本文的无缝对接JAUMIN的AFT四面体网格生成并行方法，有效地复用了串行AFT四面体网格生成算法，实现了针对复杂模型的数亿量级规模以上的高精度四面体网格的快速生成，可扩展性良好。本文方法已集成到中国工程物理研究院计算机应用研究所和高性能数值模拟软件中心联合研制的大规模复杂数值模拟的前处理软件SuperMesh V1.5[16]版中。下一步，还需要对碎片化分区问题和分区表面网格的拓扑优化算法开展研究。

[1]Mo Zeyao.Progress on high performance programming framework for numerical simulation[J].E-Science Technology&Application,2005,6(4):11-19.

[2]Lo S H.A new mesh generation schema for arbitrary planar domains[J].International Journal for Numercial Methods in Engineering,1985,21(8):1403-1426.

[3]Löhner R.Progress in grid generation via the advancing front technique[J].Engineering with Computers,1996,12(3):186-210.

[4]Alleaume A,Francez L,Loriot M,et al.Large out-of-core tetrahedral meshing[C]//Proceedings of the 16th International Meshing Roundtable,Seattle,Oct 14-17,2007.Berlin:Springer,2008:461-476.

[5]Baker T J.Developments and trends in three-dimensional mesh generation[J].Applied Numerical Mathematics,1989,5(4):275-304.

[6]Owen S J,Shelton T R.Evaluation of grid-based hex meshes for solid mechanics[J].Engineering with Computers,2015,31(3):529-543.

[7]Chen Jianjun,Xiao Zhoufang,Cao Jian,et al.Automatic hexahedral mesh generation for many-to-one sweep volumes[J].Journal of Zhejiang University:Engineering Science,2012,46(2):274-279.

[8]Antonopoulos C D,Blagojevic F,Chernikov A N,et al.A multigrain Delaunay mesh generation method for multicore SMT-based architectures[J].Journal of Parallel and Distributed Computing,2009,69(7):589-600.

[9]D3D Mesh Generator[EB/OL].(2001-05-20)[2016-08-12].http://mesh.fsv.cvut.cz/～dr/d3d.html.

[10]Tendulkar S,Beall M,Shephard M S,et al.Parallel mesh generation and adaptation for CAD geometries[EB/OL].(2012-10-12)[2016-09-05].http://www.scorec.rpi.edu/REPORTS/2011-2.pdf.

[11]Ivanov E,Gluchshenko O,Andrä H,et al.Parallel software tool for decomposing and meshing of 3D structures[EB/OL].(2008-12-21)[2016-08-12].http://www.itwm.fraunhofer.de/fileadmin/ITWM-Media/Zentral/Pdf/Berichte_ITWM/2007/bericht110.pdf.

[12]Shephard M S.Interoperable technologies for advanced petascale simulations[EB/OL].(2010-02-05)[2016-07-15].http://www.osti.gov/scitech/biblio/971531#.

[13]Karypis G,Kumar V.Multilevelk-wayhypergraph partitioning[C]//Proceedings of the 36th Conference on Design Automation,New Orleans,Jun 21-25,1999.New York:ACM,1998:343-348.

[14]Zoltan:paralllel partioning,load balancing and data-management services[EB/OL].(2007-05)[2016-09].http://www.cs.sandia.gov/Zoltan.

[15]Loop C.Smooth subdivision surfaces based on triangles[D].Salt Lake City:University of Utah,1987.

[16]SuperMesh[EB/OL].(2016-07-12)[2016-09-10].http://www.caep-scns.ac.cn/SuperMesh.php.

附中文参考文献：

[1]莫则尧.高性能数值模拟编程框架研究进展[J].科研信息化技术与应用,2015,6(4):11-19.

[7]陈建军,肖周芳,曹建,等.多源扫掠体全六面体网格自动生成算法[J].浙江大学学报:工学版,2012,46(2):274-279.