LBS中改进人工势场法的动态目标路径规划研究

陈倩，张奇松，侯丽

（大连东软信息学院信息管理系，辽宁大连116026）

基于位置服务的系统（LBS），一般是指运营商利用GPS或无线通讯网络获取移动终端用户的位置信息，在一定平台的支持下，为用户提供服务的增值业务，其中，而路径规划和人员跟踪是LBS系统的主要业务和功能[1-4]。

本文针对LBS系统中的路径规划进行了研究，由于人工势场法原理简单，计算速度快，在路径规划中广泛应用，因此对人工势场法进行了深入研究和讨论[5-6]。文献[7-8]指出传统人工势场法存在一些缺陷：无法利用全局环境信息，算法缺乏自身调节能力，在寻址过程中易陷入局部最优解，不易躲避动态障碍物，也无法追踪动态目标等问题。针对以上问题，本文提出一种改进式人工势场算法，在模型构建和搜索算法两方面进行改进，首先针对环境中的障碍物的连通性进行分析[9-10]，借助几何拓扑学获取可行解域，其次在可行解域中进行路径预规划，解决其人工势场法易陷入局部最优解而不能找到可行路径的问题，同时在人工势场中加入速度因子，使用户可以躲避动态障碍物以及追踪动态目标，最后进行曲率检查获得相对平滑的可行性路径。

1 障碍物建模及连通性分析

在LBS系统中，所处环境中静态障碍物的建模是路径规划的研究前提，静态障碍物建模的优劣直接会影响路径规划的效果，但真实环境中静态障碍物多样且未知，为简化分析，本文将障碍物全部化为圆形形状，障碍物中心为原点，影响范围为半径，同时将障碍物投影到二维平面，以此构建所处环境，环境中障碍物影响的范围随着障碍物离用户的距离的增加而减少，如图1所示，圆形表示障碍物，圆形及其内部为不可通行区域；其余部分表示可通行区域。针对实际复杂环境，单个圆形难以简单明了地描述障碍物信息，因此本文借助几何拓扑学原理，以距离相近圆形的包络弧近似表示障碍物，将路径规划问题简化为寻找能躲避圆形区域的路线问题，即将复杂的问题简单化，具体化。

连通性分析是为了进一步对静态障碍物分布及障碍物相互之间的关系影响进行分析，利用静态障碍物中心坐标及影响半径大小，分析出用户路径规划中的可行性解域，进而排除非可行性解，使搜索空间缩小，提高后续智能算法的效率。

分析步骤如下：设用户所处环境障碍物数量为，障碍物的中心坐标表示为，创建维数为下三角相交信息矩阵，判断任意与的大小，如果前者大，则设为1，反之设为0；随后根据信息矩阵中的值分析静态障碍物中起作用的相交区域，利用直线将起作用的区域中心连接起来，并将该类障碍物中心合并成一个集合。

分析结果如图1所示，在上述集合中所有障碍物中心都被直线连接，通过上述步骤，路径规划问题由避开圆形区域变为找寻起始点和终止点之间与相连线段几何问题，简化了求解问题，同时使搜索空间进一步减小，有利于提高后续智能算法的可行性和实时性。

图1 障碍物建模及连通性分析图

2 路径点预规划

路径点预规划是在对障碍物进行连通性分析基础之上进行的，预先在起始点和终止点之间找寻一条连接路径。障碍物的中心点构成了该该连接路径的中间节点，既满足了全剧规划的眼球，又可以防止后续算法—改进人工势场法陷入局部最优解，提高了后续智能算法的寻找全局最优解的能力。

具体步骤如下所示：

1）连接起始点和终止点。

2）判断有无障碍物集合与1）中连线相交，若没有相交，则结束预规划；若有相交，选定离起始点最近的障碍物集合。

3）从该集合中选出新的路径起始点

4）将新选出的起始点与终止点相连，转到2）步骤

上述2）的具体操作：描绘出所处环境中所有静态障碍物的中心集合，对于中心集合中的任意中心点，表示为x，如果满足ax＜aref或ax＞aref（a为角度），则表示连线与障碍物中心集合没有相交；否则表示两者相交。

如连线与多个障碍物中心集合有交集，对于离起始点最近集合的选择需要利用障碍物中心点在连线上的投影，然后比较连线上的投影，距离起始点最近的投影所在的障碍物中心集合即为应选取得集合。

新起始点最近的障碍物中心的选取是计算该集合中所有点x的|ax-aref|，将此值最小的点作为新的起始点。其中，ax表示障碍物中心点x与新起始点连线和坐标系的夹角，aref为终点和新起始点连线与坐标系的夹角。

3 改进人工势场法

传统人工势场法的基本思想是将用户所在的已知环境，构造一种抽象的人造势场，目标点对用户产生虚拟“引力场”，进而产生“引力”，吸引用户向其运动；障碍物对用户产生虚拟“斥力场”，进而产生“斥力”。在“引力”和“斥力”的共同作用下，用户可以顺利避开障碍物，并达到目标点。通过这种虚拟势场的构建，能够规划出起始点到终止点之间比较平滑的无障碍路径[11-13]。

传统的人工势场并不适定位、追踪动态目标以及躲避动态障碍物，其引力场函数和斥力场函数，如（1），（2）所示：

其中，ρ(q,qgoal)=‖q-qgoal‖ 是配送车辆当前位置q与目标位置qgoal之间的距离，ξ为正比例系数，m=1或 2；ρ(q,qobs)=‖q-qobs‖为当前配送车辆位置q与障碍物表面位置qobs的最短距离，ε为正比例系数，ρ0为斥力场斥力所能影响到的最大距离，超出该值，斥力场斥力不会对用户产生影响。

不难看出传统人工势场法中的引力场函数只与用户和目标点的位置有关，因此用户无法很好的躲避动态障碍物并追踪动态目标。

因此本文在传统人工势场法的基础上提出了一种新的引力场函数和斥力场函数。在函数中添加速度因子，由于速度因子是矢量，既有大小，又有方向，因此可以使用户追踪动态目标，同时在运动过程中能有效躲避静态障碍物和动态障碍物。为便于分析说明，做以下假设：

假设1：用户的位置q和速度v已知；

假设2：动态目标的位置qtar和速度vtar已知，动态障碍物的位置qobs和速度vobs亦已知。

本文将速度因子引入传统人工势场法中，提出一种改进的引力场函数和斥力场函数，表达式如公式（3），（4）所示：

其中，q(t)和qtar(t)为t时刻配送车辆和动态目标的位置，v(t)和vtar(t)为t时刻配送车辆和动态目标的速度矢量，‖qtar(t)-q(t)‖是t时刻配送车辆与动态接收实体的相对距离，‖vtar(t)-v(t)‖ 是t时刻配送车辆与动态接收实体速度的相对值，αq和αv是正比例系数，m和n是两个正的常量；q(t)和qobs(t)为t时刻配送车辆和动态障碍物的位置，v(t)和vobs(t)为t时刻配送车辆和动态障碍物的速度矢量，‖q(t)-qobs(t)‖是t时刻配送车辆与动态障碍物的相对距离，‖vobs(t)-v(t)‖ 是t时刻配送车辆与动态障碍物速度的相对值，和是正比例系数，k和S是两个正的常量。

从公式（3）可以得出，当速度因子被引入到引力场函数Uatt(q,v)中后，当且仅当用户与动态目标的相对距离和相对速度都为零时，函数值为0。新引力场函数Uatt(q,v)随着用户和动态或静态目标的相对距离或者相对速度增加而增加，可以有效定位和追踪物流中的动态目标；由公式（4）可以看出，当斥力场函数Urep(q,v)引入速度矢量后，当配送车辆距离障碍物在其影响范围之内，并且朝向障碍物（包括静态和动态障碍物）时，斥力场函数起作用，当配送车辆在障碍物影响范围之外或者两者速度相反时，障碍物斥力场不起作用，可以有效躲避环境中静态和动态障碍物。

生成路径后，为保证路径的平滑性，设定配送车辆的最大转弯角度θ，规定生成路径只能在不大于预订的角度范围内转弯，最大角度限制为±90∘。

4 算法流程

文中在对障碍物建模，进行连通性分析，其次将速度因子引进传统人工势场法中，改进引力场函数和斥力场函数，使之能够适应动态环境。整体算法如下：

1）生成障碍物模型；

2）对障碍物进行连通性分析；

3）进行路径点规划；

4）通过改进人工势场法计算生成路径；

5）判断生成路径是否在障碍物区域外；

6）如果是，根据最带转弯角度，调整生成路径，保证其平滑性；如果不是，返回第4）步，重新生成路径。

5 基于LBS系统的算法实现

文中所提算法可以基于LBS系统实现的，LBS系统不是单一系统，而是一种集成性系统[14-16]。该系统有两部分组成—移动终端和服务器端，组成部分之间通过互联网以及无线网络进行数据传输，如图2所示。

图2 基于LBS系统的算法实现

LBS系统中，用户可以利用所持移动终端设备将自己的需求，即需要追踪的动态目标，通过互联网或无限网络传送到服务器端，服务器端根据用户需求调用安装在动态目标上的配套装置—GPS装置或传感器装置，配套装置根据需求将自身以及周边障碍物的位置和速度等信息实时不断地返回给服务器端，服务器端根据本文提供的算法，实时规划相应无障碍路径，并将其结果传送到用户移动终端设备，供其使用。

6 仿真实验

为了验证本文所提算法的有效性和优越性，本文利用Matlab和Visual C++进行联合编程，构建仿真实验。为简明实验，在仿真实验中，障碍物和目标点的位置人为设定，配送车辆的步长为0.5 cm，每步间隔时间为100 ms，同时为了简化研究，实验中设定配送车辆和接收实体均为匀速运动，同时参数设置如下：引力场系数αq=2，αv=1.5，斥力场系数，m=1,n=2，k=1,s=2。为验证基于连通性分析的改进人工势场在LBS系统中的路径规划有效性和优越性，本文进行首先对本文所提算法进行仿真试验，图3，图4，图5表示基于连通性分析的改进人工势场算法，证明本文所提算法的有效性性；其次，进行对比实验，仅针对改进人工势场算法进行仿真实验，如图5所示，证明本文所提算法的优越性。在仿真实验中，左下方移动原点表示用户，图中左上位置黑色圆点表示动态目标，为体现对比实验的准确性，用户和动态目标的出发位置相同，同时为简化实验，动态目标设定为匀速直线运动，中间静止圆点为人为设置的相同静态障碍物，中间黑色移动圆点表示移动障碍物，仿真实验如下。

图3 改进算法中用户遇到障碍物

图4 基于联通性分析的改进人工势场法

通过以上实验，首先证明了基于连通性分析的改进人工势场法的有效性，在引入速度因子后，新的引力场函数和斥力场函数所产生的合力可以产生一条无障碍路径，并顺利追踪到动态目标，图3表示用户进入动态障碍物影响范围，图4表示用户成功追踪到动态目标。其次通过对比实验，如图5所示，单纯改进人工势场同样可以躲避动静态障碍物，并追踪到动态目标，但明显在路径长度上要长于本文所提算法，证明了本文所提算法的优越性。为了进一步说明本算法的高效性，本文在相同环境下将基于连通性分析的人工势场与单纯改进人工势场算法进行数值比较。其数值对比实验数据如表1所示。

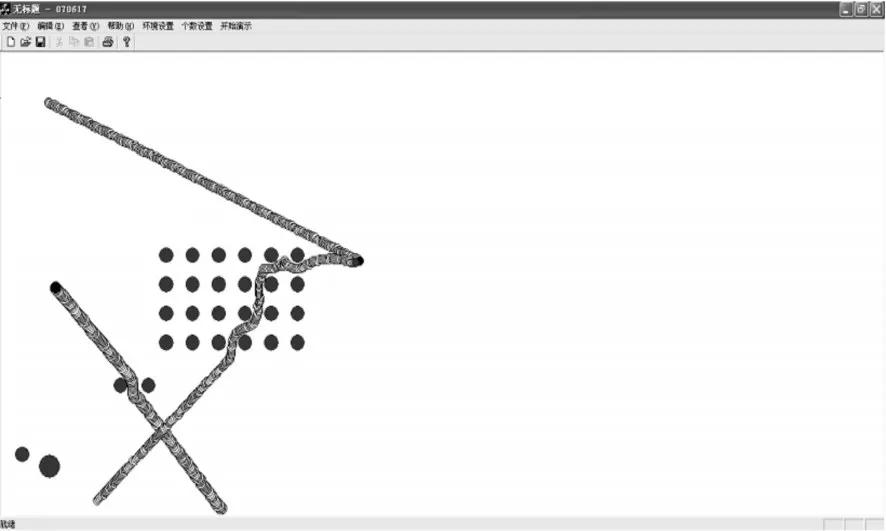
图5 单纯改进人工势场法

表1 对比实验具体数据

通过实验表明，在相同实验环境下，基于连通性分析的改进人工势场算法和单纯改进人工势场算法均能追踪到动态目标，但基于连通性分析的改进人工势场算法到达时间和运动步数均优于单纯改进人工势场算法。说明本文所提出的算法是有效的，同时明显提高了算法的搜索效率。

7 结论

文中提出了一种基于连通性分析改进式人工势场法，并将其应用于LBS系统[17]中路径规划问题。本文在连通性分析基础上，将速度因子加入到传统人工势场算法中，构造新的引力场函数和斥力场函数，进而使用户可以躲避动态障碍物及追踪动态目标，并获取最优路径。最后通过对比仿真实验表明本文所提算法的具有很高的实用性和有效性。

参考文献：

[1]陈廷斌，张奇松.基于改进人工蚁群算法的LBS最短路径研究[J].计算机仿真，2013，30（5）：349-353.

[2]彭红.基于云计算的LBS应用研究[J].软件工程，2016，19（10）：27-29.

[3]马春来，单洪，马涛，等.一种基于随机森林的LBS用户社会关系判断方法[J].计算机科学，2016，43（12）：218-222.

[4]周傲英，杨彬，金澈清.基于位置的服务架构与进展[J].计算机学报，2011，34（7）：1155-1171.

[5]翟红生，王佳欣.基于人工势场的机器人动态路径规划新方法[J].重庆邮电大学学报：自然科学版，2015，27（6）：814-818.

[6]于振中，闫继宏，赵杰，等.改进人工势场的移动机器人路径规划[J].哈尔滨工业大学学报，2011，43（1）：50-55.

[7]陈廷斌，张奇松，杨晓光.基于改进人工势场-鱼群算法的LBS最短路径修正研究[J].计算机应用与软件，2015（6）：259-262.

[8]温素芳，郭光耀.基于改进人工势场法的移动机器人路径规划[J].计算机工程与设计，2015（10）：2818-2822.

[9]黄玉强.移动机器人在未知环境下的基于视觉系统的地图创建[D].南京：南京大学，2012.

[10]王梅，王叶婷，屠大维，等.基于混合势场法的移动机器人路径规划[J].计算机应用研究，2012，29（7）：2447-2449.

[11]欧阳鑫玉，杨曙光.基于势场栅格法的移动机器人避障路径规划[J].控制工程，2014，21（1）：134-137.

[12]崔金琦，陶先平.基于RFID的校园导航系统的设计与实现[J].计算机科学，2015，12：92-94，119.

[13]吴晋，张国良，汤文俊，等.基于改进人工协调场的多机器人避碰算法[J].计算机应用，2013，33（11）：3123-3128.

[14]谭钧.基于LBS技术与O2O模式的城市共同配送研究[J].物流技术，2015（22）：126-129.

[15]袁国泉，陶先平.基于云计算平台的LBS服务管理[J].计算机科学，2011（10）：18-22.

[16]彭红.基于云计算的LBS应用研究[J].软件工程师，2016，19（10）：27-29.

[17]刘秋连.O2M全渠道视角下零售企业会员营销模式的构建[J].西安工程大学学报，2016（5）：669-674.