基于GMTS准则的岩石半圆盘试件断裂行为
陈汉林
(重庆能源职业学院,重庆 402247)
0 引言
裂纹扩展方式主要为Ⅰ-Ⅱ复合型断裂,这对于岩石材料复合型断裂强度和裂纹延伸路径等的研究意义重大[1-3]。较为经典的断裂准则主要有最大周向应力准则(MTS)[4]、最小应变能密度因子准则(S)[5]和最大能量释放率准则(G)[6]。在裂纹尖端应力场的分析中,大都采用Williams级数解的展开式,包括奇异项、常数项以及若干高阶项,其中T应力为平行于裂纹方向的常数。以上经典的断裂准则均未考虑过常数项(T应力)的影响,其预测结果,特别是复合型裂纹起裂角存在较大误差[7-8]。
研究表明[9-10],当非常接近裂尖时,奇异应力项比T应力大很多,此时T应力可以忽略。但是材料的临界裂纹扩展区半径rc较大时,T应力不能再忽略[11-12]。刘帅华等[9-14]研究了T应力对脆性材料Ⅰ-Ⅱ复合型断裂韧性及裂纹扩展路径的影响,T应力对Ⅱ型断裂占主导地位的Ⅰ-Ⅱ复合型裂纹的应力强度因子具有很大影响;唐世斌等[10]发现通过控制T应力的大小,可以对裂纹扩展方向加以控制,最大限度地防止材料断裂。Ayatollahi等[12]发现:在T应力作用下Ⅰ型和Ⅱ型断裂韧性不再是常数,而是依赖于T应力的数值,不同试件形状测试的断裂韧性值不统一;试件的尺寸和载荷加载形式决定了裂纹尖端常数项T应力的大小。Larsson等[15]研究认为T应力方向和大小可以改变裂尖周围塑性区的形状和尺寸。 Cotterel等[16]及 Fleck[17]均发现,在Ⅰ型荷载条件下的断裂分析中,T应力控制着直裂纹扩展路径的稳定性。Tvergaard等[18]还研究了塑性变形中T应力对Ⅰ型裂纹扩展阻力的影响。
为研究T应力对断裂的影响,建立更加精确的复合型断裂准则,本文在传统的MTS准则中加入了T应力,建立广义MTS准则(GMTS),采用中心直裂纹半圆盘试件,加工不同裂纹倾角的试件后,施加三点弯曲应力载荷,得到不同Ⅰ-Ⅱ复合型断裂裂纹的初始起裂角和断裂韧性。根据GMTS准则预测不同复合型断裂裂纹的初始起裂角和断裂韧性,将预测结果与实验测试结果对比,研究T应力对岩石类材料的断裂强度及裂纹扩展方向的影响规律。
1 裂纹扩展准则
1.1 裂纹尖端应力场
Williams在1957年对裂纹尖端应力场进行了分析,并给出裂纹尖端弹性应力场的无限级数展开式,其周向应力分量为

式中:n为级数,值取到2,考虑T应力的影响,忽略更高阶对应力的计算影响很小的量。
其中,裂纹尖端的Williams级数解的一阶项系数A1和B1对应于应力强度因子KⅠ和KⅡ,二阶项系数A2对应于T应力,B2对应的二阶项为0,即:
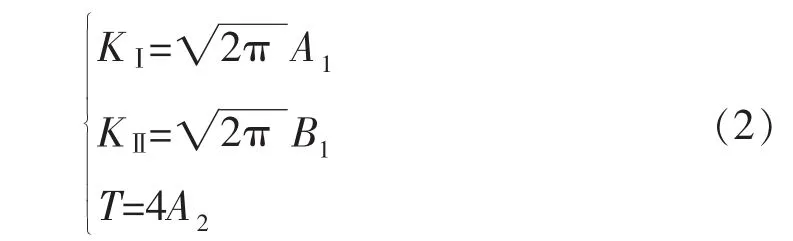
式中:σθθ为裂纹尖端周向应力,MPa;r 为圆心半径,mm;θ为裂尖周向应力方向,(°);KⅠ,KⅡ分别为Ⅰ型和Ⅱ型应力强度因子,;T 为应力,MPa。
1.2 GMTS准则
该准则认为,当裂纹尖端以圆心rc为半径的小圆周上的周向应力达到临界值σc时裂纹开始扩展,扩展方向为裂尖周向应力最大的方向,记为θc。MTS准则为

将式(1)代入式(3)可得:

对于纯Ⅰ型断裂,将 KⅡ=0代入式(4),式(5)可得:

由式(9)可以发现:在T应力为负值的情况下,二次导数始终小于0,表明式(3)在θ=0°时恒成立。因此,若T<0,则起裂角保持为0°,裂纹扩展方向不发生转向。在T应力为正值时,裂纹扩展方向只有在情况下不发生偏向。当时,式(5)无法满足,裂纹扩展角可用式(3)来预测。
2 复合型裂纹扩展分析
二维复合断裂模型,在确定参数rc,KⅠ,KⅡ,T的情况下,可求出裂纹扩展角。对式(4)无量纲化处理:
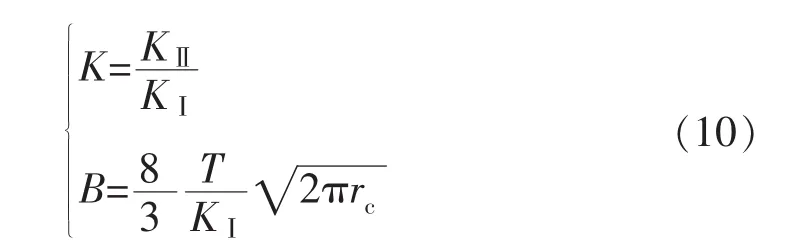

图1 广义最大周向应力准则预测起裂角
实际工程中,一般只需对 KⅠ>0,KⅡ>0 情况下材料的断裂开展研究。对于这种情况,首先根据式(8)获得确定裂纹扩展方向θc。对于纯I型裂纹,KⅡ=T=0,代入式(4)可得:

式中:KⅠc为纯Ⅰ型断裂韧性,。
对于裂纹扩展条件式(4),两边同除以 KⅠc,无量纲化处理得到:

利用式(11)对式(5)无量纲处理,两边同时除以KⅠc可得:
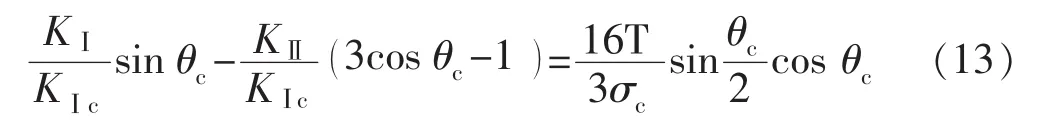

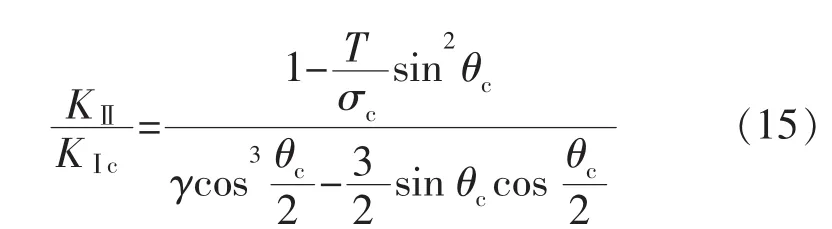
T应力的正负和数值大小取决于试件几何特征和加载情况。当裂纹试件受复合Ⅰ/Ⅱ模型荷载时,虽然应力强度因子能描述裂纹尖端的应力奇异性,但是T应力的正负和数值同样影响着断裂过程。引入无量纲参数:
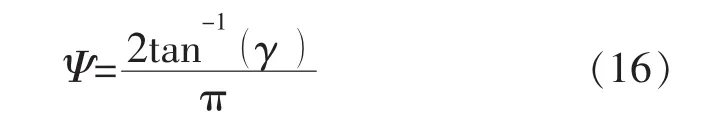
Ψ值范围为0~1,表示裂纹从纯Ⅱ型0到纯Ⅰ型1裂纹模型的变化过程。根据式(14)得到Ψ与起裂角θc的关系,本文选取几个代表值进行计算,并对相同的,利用式(15)求得应力强度因子空间中的裂纹扩展条件,如图2—3所示。

图2 T应力对裂纹开裂角影响

图3 T应力在力强度因子空间中对裂纹扩展条件的影响
3 实验及结果分析
3.1 实验概况
实验样品选用致密砂岩进行断裂韧性测试。三点弯曲半圆盘见图4。图中:R为半圆盘半径,a为预制裂缝长度,2S为支撑点间距,p为施加载荷。为满足三点弯曲半圆盘试件测试的尺寸要求,采用线切割法将直径为50 mm圆柱岩心切割为2个半圆盘,然后采用XA5032立式升降铣床,切割裂缝,刀具厚度仅为0.4 mm,设置预制相对裂纹长度为0.5 mm,相对支撑点间距S/R为0.6,裂纹倾角 α 为0°~50°共8种类型。 砂岩试件尺寸及基础物性参数见表1。

图4 三点弯曲半圆盘试件示意
实验采用自动伺服材料试验机,法向最大载荷1 200 kN,行程100 mm,可用于测量岩石的单轴抗压强度、抗拉强度、硬度等参数。选择位移加载方式控制载荷的加载,加载速率为0.1 mm/min,满足断裂韧性测试要求的准静态加载要求[11]。实验过程中,静力实验软件可自动采集载荷数据,加载至岩石发生断裂,载荷曲线跌落时停止实验。
3.2 实验结果与分析
ISRM给出的三点弯曲半圆盘断裂参数的计算公式为

式中:B 为圆盘厚度,mm;YⅠ,YⅡ和 T*为裂纹无量纲断裂参数(仅与试件尺寸有关)。

表1 三点弯曲试件基本参数
可见,断裂韧性和T应力需要无量纲断裂参数及断裂时的最大载荷共同确定,无量纲断裂参数一般采用有限元方法获得。本文采用ABAQUS软件建立了不同裂纹倾角的三点弯曲半圆盘试件模型,计算了裂纹长度比0.5、支撑点间距比0.6的SCB试件无量纲断裂参数,计算结果见文献[11]。
用GMTS准则预测材料断裂韧性时,应确定裂纹扩展区半径,Schmidt给出了裂纹扩展区半径的计算公式。无量纲参数α由裂纹扩展区半径rc和裂纹初始长度a共同来决定。对于半圆盘试样,其裂纹扩展区尺寸可为

式中:KⅠf为岩石Ⅰ型应力强度因子的临界值,,表征混合型加载下材料的断裂阻力,此处用纯Ⅰ型断裂韧性代替;σt为岩石抗拉强度,MPa。
假定裂纹扩展过程中,裂纹扩展区半径保持不变。利用式(18)求得实验样品的裂纹扩展区半径为3.6mm。
采用本文建立的GMTS准则预测三点弯曲半圆盘的起裂角,并在应力强度因子空间内预测出半圆盘试件的断裂条件,预测结果如图5—6所示。同时,为研究T应力对裂纹起裂和扩展路径的影响,将传统的MTS准则及实验数据同样绘于图中。
从图中可以看出,不考虑T应力影响的最大周向应力预测结果与实际断裂韧性实验测试结果存在很大误差,而没有忽略T应力影响的修正最大周向应力裂纹扩展判别准则预测结果更加接近实验测试数据。在裂纹倾角较小时,传统MTS准则预测结果偏小,而倾角较大时,预测结果偏大。在应力强度因子空间内,Ⅰ型断裂占主导地位时,传统MTS准则低估了断裂时刻的应力强度因子;在Ⅱ型断裂占主导地位时,传统MTS准则高估了断裂时刻的应力强度因子。通过考虑T应力的广义MTS准则、传统的MTS准则及实验数据的对比,可见不考虑T应力影响的传统MTS准则预测结果与实验结果存在较大误差,特别是对于Ⅱ型断裂占主导地位的复合型断裂,误差更大。

图5 T应力对半圆盘砂岩试样起裂角的影响

图6 T应力对半圆盘砂岩试样I/II复合型断裂韧性影响
4 结论
1)在纯Ⅰ型断裂情况下,当B超过临界值后,裂纹不再沿裂纹面即θ=0°继续扩展,且扩展角可能达到80°以上;当B<0时,不同K值时的裂纹起裂角随B的增大改变不明显,当B>0时,起裂角变化加剧。
2)当T>0时,裂纹起裂角高于不考虑T应力时的预测结果,测试断裂强度低于MTS准则的预测结果;而在T<0时,预测起裂角小于不考虑T应力的预测结果,断裂时刻的临界应力强度因子大于MTS准则的预测结果。负的T应力会增大岩石断裂强度,抑制裂纹扩展。
3)传统的MTS准则仅考虑了Williams级数解的第1项,即应力强度因子,裂纹起裂角和断裂韧性预测结果存在较大误差,而本文建立的广义最大周向应力准则由于考虑了T应力的影响,用该准则的预测结果与实验结果更加吻合,提高了预测精度。
[1]郦正能,张纪奎.工程断裂力学[M].北京:北京航空航天大学出版社,2012:61-75.
[2]刘津.T应力对混凝土断裂韧度的影响[D].大连:大连理工大学,2014.
[3]高玉华,汪洋,程长征.广义T应力对裂纹应力强度因子的影响[J].中国科学技术大学学报,2009,39(12):1319-1322.
[4]ERDOGAN F,SIH G C.On the crack extension in plates under plane loadingandtransverseshear[J].Journalof Basic Engineering,1963, 85(4):527.
[5]SIH G C.Strain-energy-density factor applied to mixed mode crack problems[J].InternationalJournalofFracture,1974,10(3):305-321.
[6]PALANISWAMYK,KNAUSSWG.Propagationofacrackundergeneral,in-planetension [J].InternationalJournalofFractureMechanics,1972,8(1):114-117.
[7]WILLIAMS M L.On the stress distribution at the base of a stationary crack[J].AsmeJournalofAppliedMechanics,1957,24:109-114.
[8]侯成,王志勇,王志华.基于修正最大切向应力准则的含中心直裂纹混凝土圆盘断裂行为研究[J].中国科学:技术科学,2016,46(4):377-386.
[9]刘帅华,李振兴.T应力对Ⅰ-Ⅱ复合型裂纹临界应力强度因子的影响[J].河南城建学院学报,2013,22(4):33-37.
[10]唐世斌,黄润秋,唐春安.T应力对岩石裂纹扩展路径及起裂强度的影响研究[J].岩土力学,2016,37(6):1521-1529.
[11]张明明.T应力对岩石断裂韧性及裂纹起裂的影响[D].成都:西南石油大学,2017.
[12]AYATOLLAHI M R,ALIHA M R M.Wide range data for crack tip parameters in two disc-type specimens under mixed mode loading[J].Computational Materials Science,2007,38(4):660-670.
[13]赵艳华,甘楠楠.T应力对混凝土断裂参数测定有效性的影响[J].大连理工大学学报,2013(4):537-542.
[14]周绍青,郭少华,李显方.T应力对岩石断裂韧度及扩展路径的影响[J].中南大学学报(自然科学版),2009,40(3):797-802.
[15]LARSSON S G,CARLSSON A J.Influence of non-singular stress terms and specimen geometry on small-scale yielding at crack tips in elasticplastic materials [J].Journal of the Mechanics&Physics of Solids,2009, 21(21):263-277.
[16]COTTERELLl B,RICE J R.Slightly curved or kinked cracks [J].International Journal of Fracture,1980,16(2):155-169.
[17]FLECK N A,HUTCHINSON J W,SUO Z.Crack path selection in a brittle adhesive layer [J].International Journal of Solids&Structures,1991,27(91):1683-1703.
[18]TVERGAARD V,HUTCHINSON J W.Effect of T-stress on mode I crack growth resistance in a ductile solid [J].International Journal of Solids&Structures,1994,31(6):823-833.

