基于粒子群优化的SVM供水管道泄漏诊断方法

王学渊 陈志刚 钟新荣 卢宁

摘 要： 供水管道泄漏会造成水资源浪费和经济损失，传统支持向量机泄漏诊断模型中存在参数选择不确定的问题，导致其分类结果不稳定。提出将粒子群进化算法应用于泄漏诊断支持向量机模型中的参数优化选择，利用粒子群群体智能优化搜索从全局迅速地迭代出合理的支持向量机的惩罚参数以及核参数，使建立的PSO?SVM管道泄漏诊断模型达到最优。实验测试表明，通过结合粒子群算法全局搜索收敛速度快的优点，有效地解决了支持向量机模型中两个重要参数优化选择的问题，提升了支持向量机分类的准确率和效率。

关键词： 供水管道； 泄漏诊断； 支持向量机； 粒子群算法； 参数优化； PSO?SVM

中图分类号： TN911.1?34； TP274.2 文献标识码： A 文章编号： 1004?373X（2018）07?0156?04

PSO?SVM based leakage diagnosis method of water supply pipeline

WANG Xueyuan1， 2， CHEN Zhigang1， 2， ZHONG Xinrong3， LU Ning1， 2

（1. School of Mechanical?electronic and Vehicle Engineering， Beijing University of Civil Engineering and Architecture， Beijing 100044， China；

2. Beijing Engineering Research Center of Monitoring for Construction Safety， Beijing 100044， China；

3. Changqing Downhole Technology Company， Xian 710000， China）

Abstract： The leakage of water supply pipeline will cause the water resource waste and economic losses. The traditional leakage diagnosis model based on support vector machine （SVM） has the problem of uncertain parameter selection， which may cause the unstable classification result. The particle swarm optimization （PSO） algorithm is proposed for parameter optimization selection in leakage diagnosis model based on SVM. The particle swarm intelligent optimization search is used to quickly iterate the reasonable penalty parameter and kernel parameter of SVM in the overall situation， so as to make the pipeline leakage diagnosis model based on PSO?SVM optimal. The experimental results show that， in combination with the fast convergence speed of PSO global search， the method can solve the two important parameters optimization selection problem in SVM model， and improve the accuracy and efficiency of SVM classification.

Keywords： water supply pipeline； leakage diagnosis； SVM； PSO； parameter optimization； PSO?SVM

0 引 言

随着我国城市化水平不断提高，供水管道长度呈现加速增长趋势，但供水管网道的漏损现象却十分普遍。对于城市供水管道的漏失诊断，如何从复杂干扰中识别泄漏是整个技术的关键难点[1]。针对这一关键点，文献[2]提出基于神经网络的管道泄漏检测识别方法，很大程度上提升了泄漏检测的准确率。但是，神经网络存在训练样本需求多、收敛速度慢等问题，文献[3]提出基于结构风险最小化的SVM理论应用于管道泄漏诊断领域，它在小样本及非线性的情形下有独特优势，可以实现对管道泄漏进行比较精确的诊断。但有研究表明，在成熟的条件下核函数对SVM识别性能的影响不大，其中对SVM性能起到关键作用的因素[4]是核参数和惩罚因子[C。]常规支持向量机核参数和惩罚因子的选择一般采用试凑法、经验法或单目标优化法，上述方法不能达到全局优化的效果，而且耗费时间。

本文提出将粒子群进化算法应用于支持向量机的核参数和惩罚因子的选择中。粒子群优化算法在每次迭代中都考虑了全局搜索和局部搜索，与支持向量机结合后可获得诊断效果更佳的PSO?SVM模型，提高了供水管道工况识别的准确率。

1 支持向量机

1.1 支持向量机的基本原理

支持向量机是一种实现结构风险最小化原则的分类学习算法，它利用核函数把样本映射到高维特征空间，然后在此空间中构造分类间隔最大的线性分类超平面，因而向量机比较适合于小样本数据的分类[5]。

支持向量机方法的最优分类面是在线性可分的情况下提出的。图1为最优分类界限，图中的[H]为两种样本的分类线，[H1，H2]分别为各类中离分类线最近且平行的直线，[H1，H2]之间的距离称为分类间隔。最优分类线即为分类间隔最大的分类线，使两类样本正确分离。

在线性不可分的情况下，图1所示的最优分类面在实际应用中可能存在某些样本不能被超平面正确分类的情况，超平面约束条件为：

式中：[b]为阈值；[ω]为分类面的法向量。对于非线性最优分类面的求解需要引入拉格朗日乘子，广义最优分类面问题可以转化为在约束条件下的最小化[iaii，jaiajxixjyiyj，]其中约束为[0≤ai≤C；][iaiyi=0；]惩罚参数[C]为非负常数。

对于支持向量机的非线性划分，可通过非线性变换将其转换为高维空间中的线性划分。这里只需要将原来空间的函数在高维特征空间通过内积运算的方式引入核函数，并且采用适当的内积核函数[Kxi，yi]使核函数满足Mercer条件，就可实现此非线性变换，并且算法的复杂程度也不会有所增加，此时分类函数为：

其中，影响识别准确率的两个重要因素为：

1） 核参数

核参数的改变本质上是映射函数的改变，从而改变了空间样本集分布的复杂程度。所以，只有使用适合的核函数以及核参数才能够将样本数据映射到适合的特征空间。即选择机器学习实际风险最小的特征空间，才可以获得泛化能力优秀的支持向量机分类器。

常用的核函数有径向基函数（其中函数宽度为核参数）、多项式核函数（其中多项式系数为核参数）以及Sigmoid核函数（其中尺度和衰减系数为核参数）。

2） 惩罚因子

惩罚因子[C]的数值表示对经验误差的敏感程度，惩罚因子与SVM的复杂度成正比，而与经验风险成反比。在确定的数据子空间内至少存在一个适合的惩罚因子使得SVM的泛化能力达到最好。

1.2 多元支持向量机

支持向量机是两类分类器，而现实中管道泄漏诊断结果的分类通常是多个种类，如正常输送、调阀、停泵和泄漏。常用构建多元支持向量机的方法有一对一、一对多以及采用决策树的支持向量机。

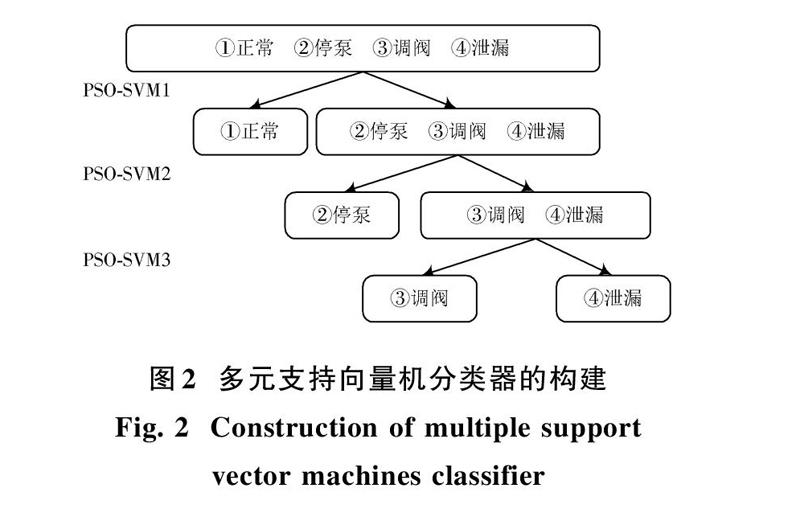
在少量的工况分类情况下，三种方法效果相当，但考虑到扩增工况识别的可能，本文采用文献[6]中的决策树方法构建多元支持向量机用以判别管道泄漏和各种工况操作。其训练效果与一对一多元支持向量机相当，但学习训练和测试用时方面比常规支持向量机更短，随着分类数量的增加，效果更加明显，效率更高。多元支持向量机分类器的构建如图2所示。

2 粒子群算法优化支持向量机

2.1 粒子群优化算法

粒子群优化算法的基本思想为：需要被优化问题的潜在解就是在空间中搜索最优粒子，将PSO算法随机初始化为随机粒子群，每个单独粒子都有一个函数决定它所对应的适应度，并且还有一个决定它们运行轨迹的速度向量，然后粒子群会依据当前的最优粒子在空间中进行搜索，直到通过迭代寻优找到最优解[7]。

粒子群优化算法核心迭代公式如下：

式中：[vk+1i]表示第[i]个粒子在第[k+1]代时的飞行速度；[xk+1i]表示第[i]个粒子在第[k+1]代时的位置；[pki]表示第[i]个粒子到第[k]代为止所找到的最优位置；[pkg]表示当前种群到目前为止所找到的最优位置；[pki-xki]表示個体认知；[pkg-xki]表示社会认知；[ω]为惯性系数，表示相信自己的程度；学习因子[c1，c2]为非负常数，前者表示对经验的信服程度，后者表示对周围个体的信服程度；[r1，r2]表示[（0，1）]的随机数。

在整个粒子群的迭代中体现了粒子群优化在寻找最优解的过程中既保持了粒子自身的惯性，又利用个性以及社会性不断修改和移动自身方向，最终使群体朝着最优解靠近，并且避免了复杂的遗传操作。

2.2 基于粒子群优化的支持向量机

根据粒子群优化算法的全局搜索优势进行支持向量机的改进，其步骤如下：

步骤1：初始化。对样本数据进行归一化处理并读取样本数据。设定参数运动范围，设定学习因子[c1，c2、]进化代数[（E）、]惩罚因子[C]和核参数[g]（本文采用径向基核函数，其核参数为函数宽度[σ]）。

步骤2：适应度评价。计算个体的适应度值，初始化个体和全局最优位置。

步骤3：比较寻优。根据式（3）更新粒子的速度和位置产生新种群，计算新种群的个体适应度值。分别比较当前参数[C]和[σ]的适应值和自身历史最优值及种群最优值，更新种群参数[C]和[σ]的全局最优值。

步骤4：检查结束条件。寻优达到最大进化代数，结束寻优，否则返回步骤2，输出最佳参数[C]和[σ]。

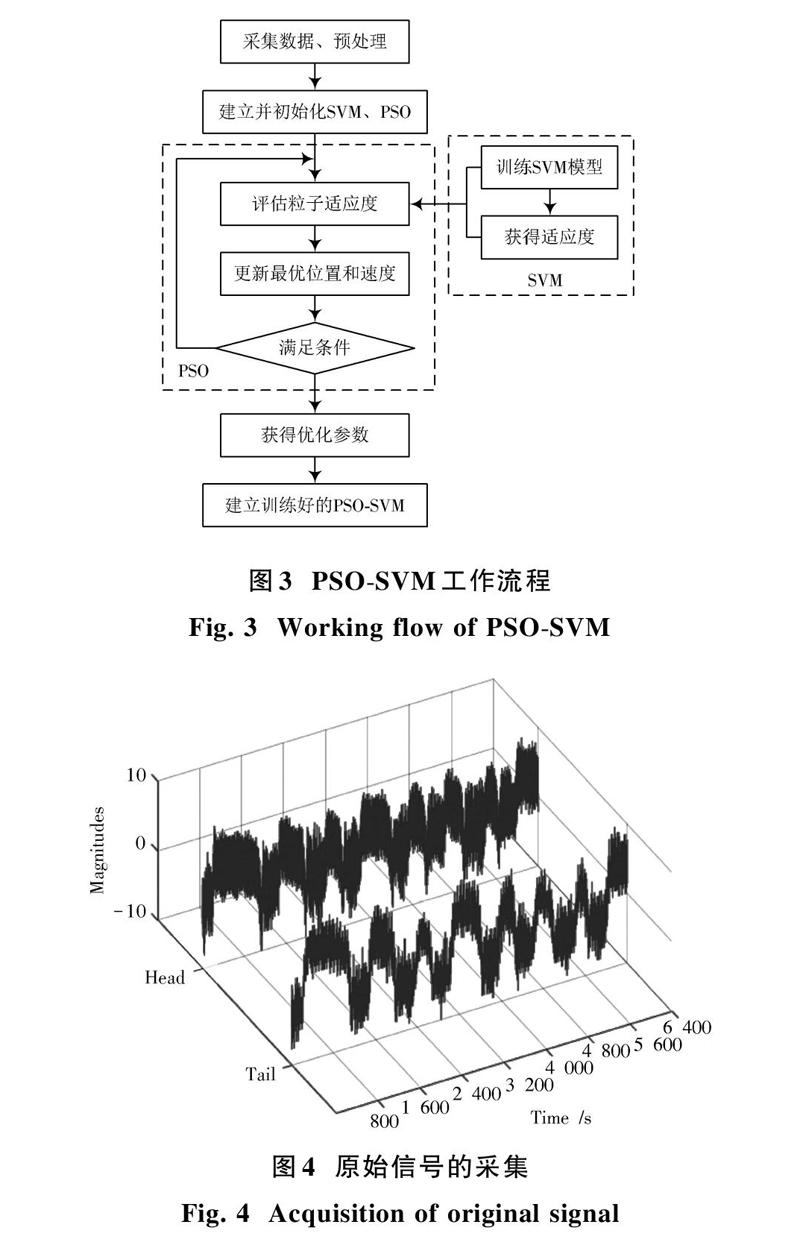
随后将优化的参数[C]和[σ]代入SVM模型并检测SVM的建模精度。PSO?SVM工作流程如图3所示。

3 应 用

3.1 实验预处理

在实际生产中，除了泄漏可能引起压力波动外，其他的一些工况操作，如启停泵、调泵、阀门切换、调阀等同样也会引起压力波动信号，而且某些工况下的波动信号与泄漏引发的波动信号非常相似。

从图4中可以看出，信号中的背景十分嘈杂，波动的特征被淹没在噪声中，不便于后期的机器学习分类。管道泄漏分析中必须对泄漏、停泵、调泵、调阀等引起的压力波动信号加以准确区别。首先要对采集的信号进行滤波，本文采用小波降噪方法进行降噪处理，得到比较纯净的波形，以便于管道的泄漏诊断。

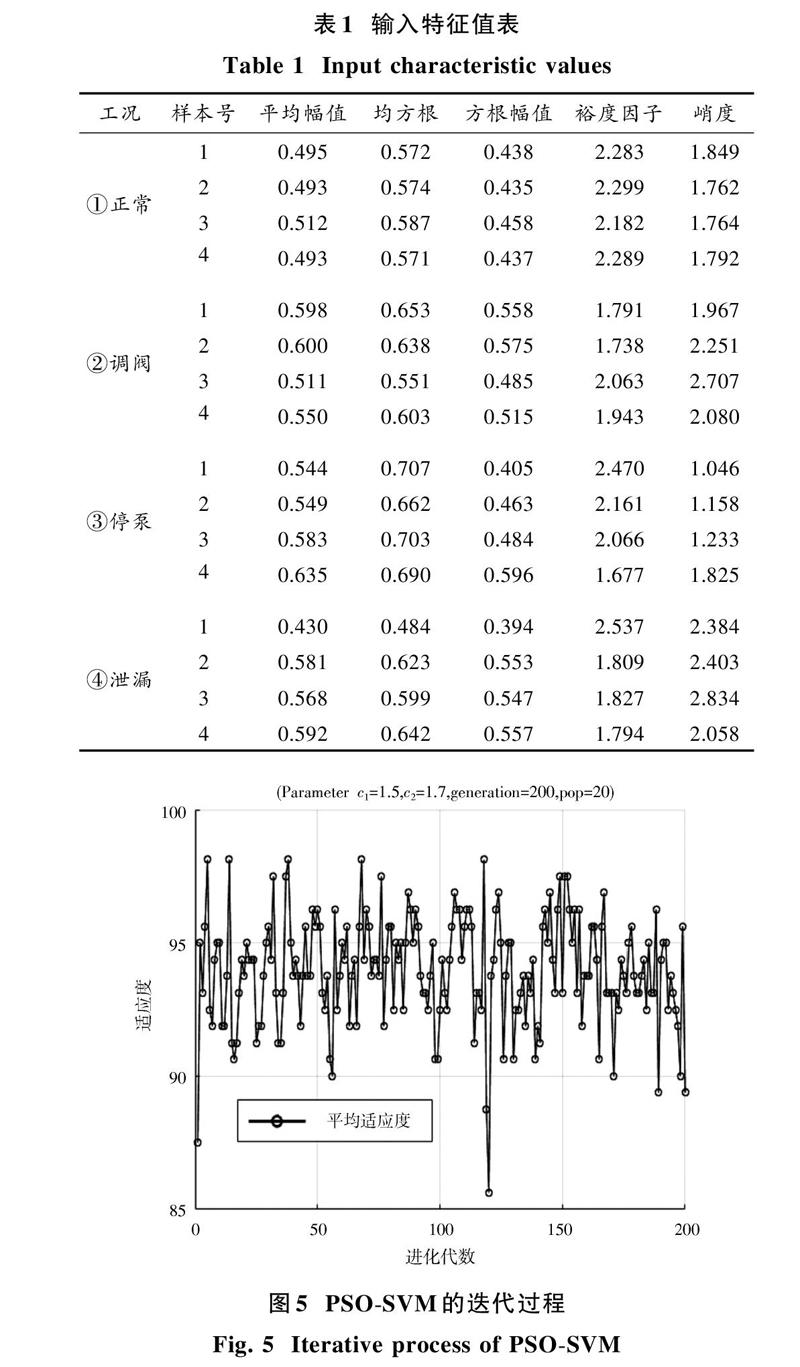
其次，泄漏波形特征参数的选择对泄漏诊断的准确率和可靠性有一定的影响。文献[8]中数据挖掘方法从描述供水管道压力波动的特征参数中选择平均幅值、均方根、方根幅值、裕度因子和峭度作为支持向量机的输入特征。输入特征值如表1所示。

3.2 参数的确定

本文采用Matlab进行模型的建造，其中核函数选择在泄漏检测领域支持向量机常用的RBF径向基[9?10]核函数：[K（x，y）=exp-x-y2σ2]。

按照本文2.2节步骤建立PSO?SVM模型，核参数及惩罚参数的迭代如图5所示。得出最优参数为：函数宽度[σ=30，]惩罚参数[C=1.5。]

由图5可以看出，随着粒子群算法迭代的进行，模型的准确率在87%～98%的区间内震荡，粒子群记录下最优的参数组合。相比以往的交叉验证和网格搜索，粒子群算法在搜索范围及速度方面都有比较明显的优势。

3.3 测试结果

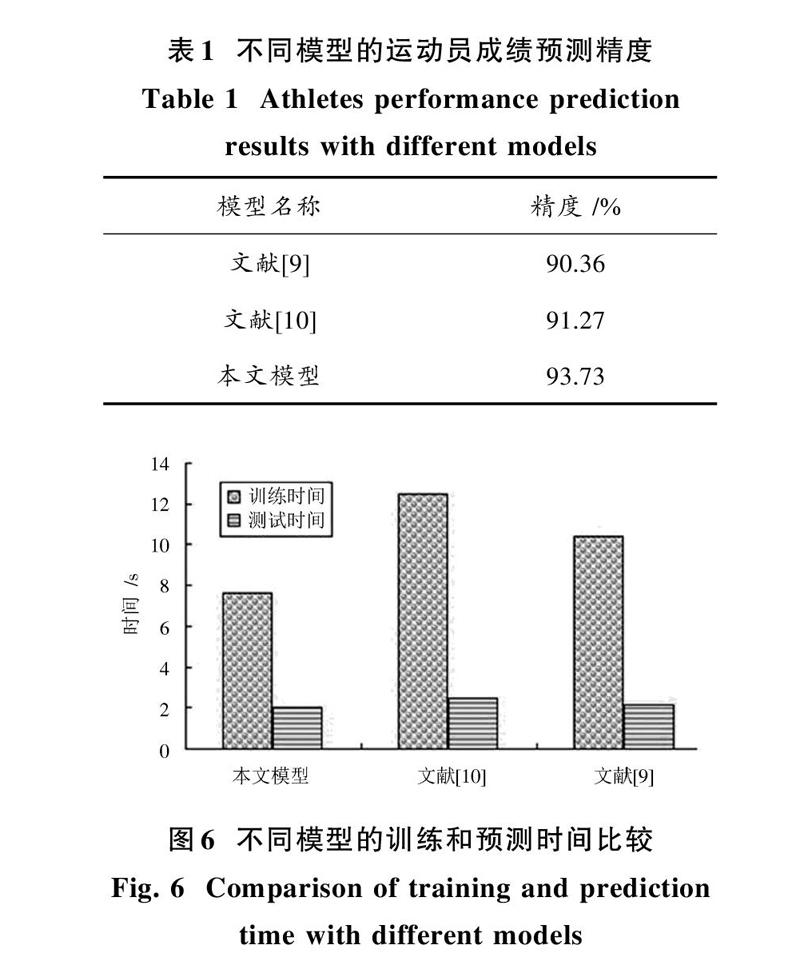
为了验证本文PSO?SVM分类模型的泛化能力，用经过训练的PSO?SVM分类器对4种运行工况下不同的样本波形进行识别分类的检测实验。将待测试样本的特征值列表按照规定的输入格式输入经过PSO?SVM训练的模型进行工况识别。为了体现基于粒子群算法的支持向量机的优缺点，建立BP神经网络以及传统的SVM模型，并将他们与PSO?SVM进行性能比较。测试结果如表2所示。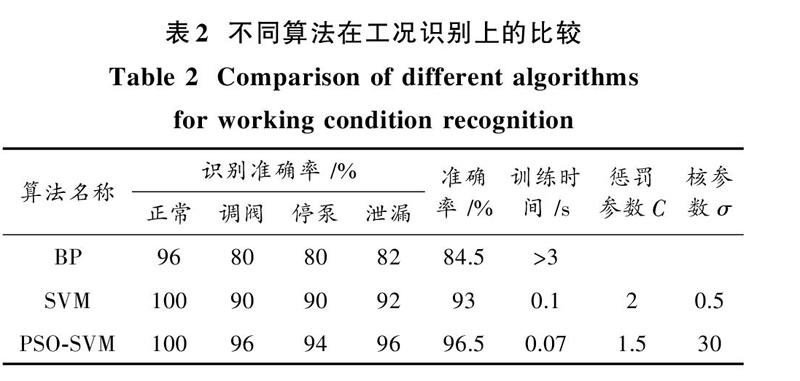

由表2可以看出，PSO?SVM相对于传统的BP神经网络和SVM不仅识别的准确率有所提升，而且训练用时相对较少，并且管道工况识别准确率分别提高了12%和3.5%。

为了降低常规操作导致的供水管道泄漏检测的错误识别，采用SVM分类器从不同的工作环境中识别出泄漏的存在；采用PSO算法對模型参数进行优化，提高了SVM分类器的泄漏识别准确率。试验结果表明，PSO比较适用于优化SVM，PSO?SVM算法对供水管道工况识别具有很高的辨识精度，可以很好地应用于相关的管道泄漏诊断中。

4 结 论

本文使用粒子群优化算法的全局优化特性优化支持向量机的核参数和惩罚参数，建立供水管道泄漏诊断模型。通过粒子群优化算法的全局搜索优势对支持向量机进行改进，使得支持向量机的参数选择更加合理。实验表明，基于改进的支持向量机的管道泄漏诊断模型在测试中准确率相对于以往的支持向量机以及神经网络模型有较明显提升，有效地解决了传统支持向量机中参数选择对检测准确率的影响，提升了对管道工况的辨识程度，同时也避免了复杂的遗传操作，在训练时间上有可观的改进。

注：本文通讯作者为陈志刚。

参考文献

[1] 文玉梅，张雪园，文静，等.依据声信号频率分布和复杂度的供水管道泄漏辨识[J].仪器仪表学报，2014，35（6）：1223?1229.

WEN Y M， ZHANG X Y， WEN J， et al. Identification of water pipeline leakage based on acoustic signal frequency distribution and complexity [J]. Chinese journal of scientific instrument， 2014， 35（6）： 1223?1229.

[2] 唐秀家.管道系统泄漏检测神经网络与模式识别方法[J].核科学与工程，1998（3）：33?40.

TANG X J. Fluid pipeline system leak detection based on neural network and pattern recognition [J]. Chinese journal of nuclearence & engineering， 1998（3）： 33?40.

[3] 陈志刚，张来斌，梁伟，等.复杂工况下热油管道泄漏识别与定位方法研究[J].西南石油大学学报，2008，30（6）：157?160.

CHEN Z G， ZHANG L B， LIANG W， et al. Leak detection and positioning for hot oil pipeline under complicated conditions [J]. Journal of Southwest Petroleum University， 2008， 30（6）： 157?160.

[4] VAPNIK V N. The nature of statistical learning theory [M]. 2nd ed. New York： Springer， 2000.

[5] CHEN Peng， YUAN Lifen， HE Yigang， et al. An improved SVM classifier based on double chains quantum genetic algorithm and its application in analogue circuit diagnosis [J]. Neurocomputing， 2015， 211： 202?211.

[6] 张亮，陈志刚，杨建伟，等.基于决策树与多元支持向量机的齿轮箱早期故障诊断方法[J].计算机测量与控制，2016（1）：12?15.

ZHANG L， CHEN Z G， YANG J W， et al. Early fault diagnosis of gearbox based on multiclass support vector machine and decision tree [J]. Computer measurement & control， 2016（1）： 12?15.

[7] TUNGADIO D H， JORDAAN J A， SITI M W. Power system state estimation solution using modified models of PSO algorithm： comparative study [J]. Measurement， 2016， 92： 508?523.

[8] 梁伟，张来斌，王朝晖.基于数据挖掘的负压波特征参数优化方法[J].石油机械，2008，36（12）：38?42.

LIANG W， ZHANG L B， WANG Z H. Study of optimization method of characteristic parameters of negative pressure wave based on data mining [J]. China petroleum machinery， 2008， 36（12）： 38?42.

[9] YIN Shen， YIN Jiapeng. Tuning kernel parameters for SVM based on expected square distance ratio [J]. Information sciences， 2016（2）： 370?371.

[10] LIU Chao， YIN Shiqun， ZHANG Miao， et al. An improved grid search algorithm for parameters optimization on SVM [J]. Applied mechanics and materials， 2014， 644： 2216?2219.