Hilbert模量与MUSIC相结合的感应电机转子断条故障检测方法

张正勇，苟旭丹，严居斌，陈健飞，张玉鸿(.国网四川省电力公司经济技术研究院，四川 成都　6004; 2.成都城电电力工程设计有限公司，四川 成都　6004)

0　引　言

异步电动机转子断条故障在常见电机故障中占有较高的比例，其将导致电动机运行性能下降，严重时电机会因此无法驱动负载而出现堵转、停转，甚至烧坏电机，威胁工业生产的可靠性和安全性，同时增加生产成本[1]。因此对该故障及早进行检测颇为重要。

研究表明，定子电流中包含电机的故障特征，因而通过提取定子电流故障特征可以准确地检测电机故障[2]。当电机发生转子断条故障时定子电流中便会出现(1+2s)f1频率分量(f1为供电频率，即定子电流基频分量，s为转差率)时，因此可以以该边频分量作为断条故障的特征向量[3]。

在众多电机故障诊断方法中，FFT是最常用的电流特性分析方法，可是直接基于定子电流的FFT方法也存在诸多缺陷。尤其是当电机负载比较小时，转差率s非常低，边频分量(1+2s)f1极其接近基频f1，同时边频分量的幅值较基频很小且由于噪声干扰，这就导致边频分量极易被淹没，此时基于FFT的定子电流特征分量提取方法的精确度表现比较逊色[4]。

从而，文献[5]使用混合骨干微粒群优化算法获得基波参数后构造出基波表达式，并将其从原始信号中剔除，以突出故障特征频率成分，但此方法过程繁琐，计算量大；文献[6]采用PARK矢量变换把基波成分转换成直流信号从而使故障特征更加明显，但该方法需要同时采集定子三相电流，增加了硬件和软件的费用。

文献[7-10]引入MUSIC算法提高了频率分辨率，同时对于短时采样信号也具有良好的性能。因此本文将Hilbert模量与MUSIC相结合用于异步电动机转子断条故障检测，既可以消除工频分量的影响，提高检测精度，又可以缩短采样时间，提高检测及时性。

1　Hilbert量模

将给定信号x(t)经过Hilbert变换就可以得到以下表达式[11]：

(1)

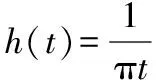
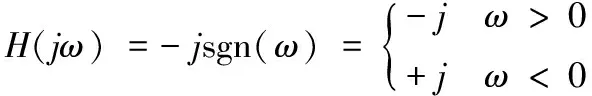
(2)

将信号进行Hilbert变换，正频率做-90°移相，负频率做+90°移相，而幅值不变化。

当异步电动机转子发生断条故障时，定子电流中会出现边频分量fb=(1±2ks)f1(为简化起见，令k=1)，故定子一相的电流便可以用下列形式表达[12]：

i=Ifcos(ωt-α)+Idlcos[(1-2s)ωt-βl]+
Idrcos[(1+2s)ωt-βr]

(3)

式中：If、α为基波电流f1的幅值、初相位；Idl、βl为左边频分量(1-2s)f1的幅值、初相位；Idr、βr为右边频分量(1+2s)f1的幅值、初相位。

将式(3)进行Hilbert变换，得到式(4)：

(4)

则Hilbert模量为：

(5)

由式(5)可以看出，转子断条时Hilbert模量的主要成分为直流、2sf1、4sf1。因为原定子电流中基频分量变为直流分量，降低了其对特征分量的影响，故将2sf1、4sf1分量作为感应电机转子断条故障诊断的特征分量是可行的。此方法由于只需要采集一相定子即可，相比Park矢量方法在软硬件成本上大幅度减少。

2　MUSIC

MUSIC是一种基于矩阵特征值分解的方法，其原理如下。

采样信号x(n)用p个谐波分量的组合表示：

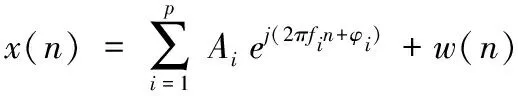
(6)

式中：p、N分别为谐波个数和采样点数；fi、Ai、φi则表示第i个谐波的频率、幅值、初相角；w(n)为零均值、方差为σ2的白噪声。

引入一个m×N阶矩阵(一般取m=3N/4以保证m≥p)。

X(n)=[x(n)x(n+1) …x(n+m-1)]H

(7)

则X(n)的自相关矩阵为:

RXX=E{X(n)XH(n)}

(8)

式中:H表示共轭转置;E表示数学期望。

MUSIC算法的步骤如下：

步骤1：构造相关矩阵RXX并将其进行特征值分解。

步骤2：将步骤1中的特征值按降序排列，同时定前p个为主特征值，后m-p个为次特征值σ2，然后求出所有特征值对应的特征向量vi(i=1,2,3,…,m)。

步骤3：构造谱估计表达式：

(9)

式中:s(fi)=[1ej2πfi…ej2π(N-1)fi]H。

步骤4：取fi=Δf，计算P(fi)。Δf即为频率分辨率，本文取值为0.001 Hz。

步骤5：根据计算结果搜索出最大的p个峰值所对应的频率f1，f2，…fp即为所求。

3　转子断条故障仿真

采用式(4)模拟异步电动机转子断条时定子电流信号：

is=A1cos(2πf1t+φ1)+A2cos[2π(1-2s)f1t+φ2]+
A3cos[2π(1+2s)f1t+φ3]+e(t)

(10)

式中:e(t)为模拟电机运行过程中的噪声。

模拟信号的各个参数赋值如表1所示。

表1　仿真参数赋值

以采样频率为fs=5 000 Hz，转差率s=0.018，采样时间t=1.5 s对仿真信号进行仿真。Hilbert模量及故障特征信号频谱如图1所示。

图1　仿真结果(s=0.018)

由仿真结果可以分析得出：Hilbert模量可以滤除定子电流信号中的基频信号，同时降低噪声干扰，MUSIC可以准确检测出电机断条故障特征频率。文中所提方法可用于异步电动机转子断条故障检测。

4　试验验证

试验采用的电机型号为Y132M-4型感应电机，其技术参数如表2所示。

表2　试验电机主要技术参数

通过在电机导条距端环10 mm处打钻孔的方式模拟工程实际中的断条故障，其中一个转子只有一根导条有钻孔，如图2所示(一根断条)，另一个转子连续两根导条有钻孔，如图3所示(两根断条)，同时以一台磁粉制动器作为负载。通过调节与磁粉制动器配套的张力控制器的输出电流改变负载大小。转子一根断条时转差率s=0.03，转子两根断条时转差率s=0.04。

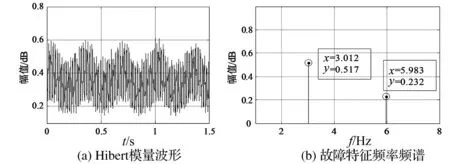
图2　试验结果(一根断条)

图3　试验结果(两根断条)

由试验结果可知，经过Hilbert模量变换之后的定子电流可以有效剔除基频分量的干扰，凸显特征分量，便于故障辨识。而借助MUSIC算法的高分辨率性能提高了故障特征频率提取能力，同时由于其需要采集的数据少，大大减少了计算量，提高了运算速度，为异步电机转子断条故障在线检测与诊断提供可能。

由于采用MUSIC算法进行频率估计时可能产生虚假频率，故采用转子齿槽谐波转差率估计技术解决MUSIC可能产生虚假频率的问题。首先通过包含于定子电流中的齿槽谐波分量确定转差率s，进而便可以确定特征频率2sf1、4sf1的大小。

5　结束语

通过将Hilbert模量与MUSIC算法相结合的感应电机转子断条故障检测方法用于仿真模拟和实际试验，可以得出以下结论：

(1)经过Hilbert模量变换的定子电流可以有效转工频量为直流量，从而避免工频量对特征量的干扰；

(2)MUSIC算法需要数据量小，计算速度快，频率分辨率高，可以快速有效检测出特征频率大小；

(3)Hilbert模量与MUSIC相结合的故障检测方法不能反应故障特征频率的幅值大小，因而无法准确反应电机断条故障严重程度，亟需要进一步予以解决；

(4)通过仿真与试验得出Hilbert模量与MUSIC相结合的故障检测方法用于感应电机转子断条故障检测是行之有效的。

参考文献：

[ 1 ] 刘振兴, 尹项根, 张哲, 等. 基于瞬时功率信号频谱分析的鼠笼式异步电动机转子故障在线诊断方法[J]. 中国电机工程学报, 2003,23(10):148-152.

[ 2 ] DELEROI W. Broken bar in a squirrel-cage rotor of an induction motor[J]. Archive for Electrical Engineering, 1984,67(3):141-149.

[ 3 ] 张建文. 电气设备故障诊断技术[M]. 北京:中国水利水电出版社, 2006.

[ 4 ] 史丽萍, 王攀攀, 胡泳军, 等. 基于骨干微粒群算法和支持向量机的电机转子断条故障诊断[J]. 电工技术学报, 2014，14(1)：147-155.

[ 5 ] 王攀攀, 史丽萍, 张勇, 等. 采用一种混合骨干微粒群优化算法的感应电机转子断条故障诊断[J]. 中国电机工程学报, 2012,32(30):73-81.

[ 6 ] 邵英. 采用Park变换感应电机转子复合故障检测[J]. 电机与控制学报, 2010,14(3):57-61.

[ 7 ] 朱天敬, 许伯强. MUSIC和Prony在电动机断条故障检测中的应用[J]. 电力系统及其自动化学报, 2015,27(1):54-59.

[ 8 ] 孙丽玲, 许伯强, 李志远. 基于MUSIC与SAA的笼型异步电动机转子断条故障检测[J]. 电工技术学报, 2012,12(27):205-212.

[ 9 ] 许伯强, 孙丽玲, 李和明. 基于多重信号分类与模式搜索算法的笼型异步电动机转子断条故障检测新方法[J]. 中国电机工程学报, 2012,32(9):93-99.

[10] 许伯强, 孙丽玲, 李和明. 基于高频率分辨力谱估计技术与优化算法的异步电动机转子故障检测新方法[J]. 中国电机工程学报, 2013,33(3):140-147.

[11] 赵淑青, 郑薇. 随机信号分析[M]. 北京:电子工业出版社, 2011.

[12] 张贤达. 现代信号处理[M].2版. 北京:清华大学出版社, 2002.