计及分布式电源功率不确定性的配电网多目标无功优化

潘曙冰， 陆政， 高莹， 汪立俊， 周武(.国网江苏省电力公司常州供电公司，江苏 常州　3003；.武汉大学 电气工程学院，湖北 武汉　43007)

0　引　言

高渗透率分布式风力和光伏发电单元接入运行是配电网的必然发展趋势[1]。然而，在风速、光照等自然环境因素的影响下，这些分布式发电的出力具有较强的随机性和波动性。传统配电网无功优化是通过投入合理的无功补偿来优化系统的无功潮流分布[2]，以减小系统有功网损和提高电压质量等，但所采用的无功优化方法基本未考虑用电负荷随机性等不确定性因素的影响，所得到的优化方案适应性较差，出力强随机性的分布式发电并网将进一步对配电网无功优化提出新的挑战。

文献[3]针对含有分布式电源的配电网无功优化问题，提出一种将入侵杂草算法和差分进化算法相结合的方法，但分布式电源采用恒功率模型，未计及分布式电源出力的不确定性。文献[4-5]利用场景分析法将风电场的出力等效为零输出、欠额定和额定3个场景，并分别对每个场景按照传统的确定性方法进行无功优化，但将风电输出随机性简化为3个场景太简单和粗糙。文献[6]考虑了两个风电场接入配网引起的不确定性问题，采用基于拉丁超立方采样的蒙特卡罗概率潮流计算方法，并利用场景缩减技术处理无功优化中的随机性问题，但并未考虑光伏发电和负荷的不确定性。

本文考虑了配电网无功优化中分布式电源出力和负荷功率的不确定性，通过建立负荷与分布式电源出力的概率模型，采用两点估计法解决概率潮流问题。针对风电场和光伏系统接入出力及负荷功率的不确定性，建立了有功网损和节点电压偏差最小为多目标的配电网无功优化模型，采用NDX-NSGA2算法进行模型求解。最后对IEEE33节点配电系统中的算例进行仿真，结果表明NDX-NSGA2算法的优化效果优于常规NSGA2 算法，且两点估计法的计算结果与蒙特卡罗法的结果非常接近，验证了本文所提方法的正确性和有效性。

1　配电网多目标无功优化模型

1.1　目标函数

本文以有功网损PL最小和电压水平最好(即节点电压偏差dV最小)作为无功优化问题的双目标，即：

(1)配网有功网损PL

配网系统有功网损计算公式为：

(1)

式中：Nl为配网系统的支路数；Gk是支路k的电导；Ui和Uj分别是节点i和j的电压有效值；θij是节点i和节点j间的电压相角差。

(2)节点电压偏差dV

节点电压偏差dV可表示为：

(2)

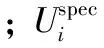
1.2　约束条件

(1)功率平衡等式约束

(3)

式中：N为配网系统的总节点数；Gij和Bij分别为节点i和j间线路的电导和电纳；PDGi和QDGi分别为分布式电源在节点i输出的有功和无功功率；PLi和QLi分别为节点i负荷的有功和无功功率；QCi为节点i处无功补偿容量大小。

(2)不等式约束

配电网无功优化的不等式约束包括控制变量约束以及状态变量约束，控制变量约束包括无功补偿容量约束和变压器分接头约束，且其均为离散变量。状态变量约束包括各节点的电压有效值大小约束。此外分布式电源具有接入容量约束。

(4)

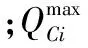
2　分布式电源和负荷概率功率模型及潮流计算

2.1　负荷概率模型

一般认为基于预测的负荷功率具有正态分布[7]，分别用μD和σD表示负荷有功功率的期望值和方差，用μD和σD表示负荷无功功率的期望值和方差，则负荷有功和无功功率的概率密度函数可表示为：

(5)

2.2　风电出力概率模型

风速是不断变化和不可预测的，通常采用威布尔分布来对风速进行统计描述[8]，其概率密度函数可表示为：

(6)

式中：K和C分别为威布尔分布的形状参数和尺度参数。K和C可采用平均风速和标准差估计法获得[9]：

(7)

(8)

式中：μv和σv分别为风速的期望和方差，可通过风速的统计数据获得。

风电场的出力是风速的函数，风速的随机性决定了风电场输出功率的波动性，使得其输出功率在0和额定功率之间变化。其输出功率可表示为：

(9)

式中：Pr、vr分别为风机的额定功率和额定风速；vci、vco分别为风机的切入和切除风速。

2.3　光伏出力概率模型

一般认为太阳能光照强度近似服从Beta分布[10]，即：

(10)

式中：rmax和r分别为某一时段内的最大光照强度和实际的光照强度(W/m2)，α、β为Beta分布的形状参数。

对于一个包含有M个电池组件的太阳能阵列，其总的输出功率为：

PM=rAη

(11)

式中：A为太阳能电池阵列的总面积，η为阵列的光电转换效率。

2.4　基于两点估计法的概率潮流计算

蒙特卡罗法模拟成千上万次，需要很长的计算时间，一般作为对比方法来评价其他概率方法的优劣[11]。两点估计法(two-point estimate method, TPEM)是一种近似求解的方法[12]，通过在每个随机变量的均值两侧确定两个值，将对节点注入量的求解问题分成若干个子问题，在每一个随机变量处用均值两侧的值来代替，同时其随机变量取均值。假设系统含有n个不确定量，那么需要对该系统进行2n次确定性潮流计算。将节点注入向量X可表示为：

X=[x1,x2,…,xn]T

(12)

配电网系统网损和节点电压偏差可表示为节点注入量的函数：

(13)

利用两点估计算出每一节点注入随机量xi均值aver_xi两侧的两个变量xi1和xi2来匹配随机量的前三阶矩，计算过程见文献[12]。对于随机量xi用xi1、xi2代替，其它的随机量均设为均值，则可形成2×n组数据，用2×n组数据来进行确定性潮流计算：

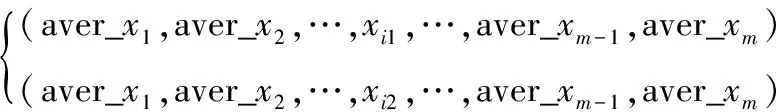
(14)

经过计算可得到系统网损和节点电压偏差两个估计PL(i,1)、PL(i,2)和dV(i,1)、dV(i,1) (i=1,2,…,n)。配电网系统网损和节点电压偏差可通过下式求解：

(15)

3　基于NDX-NSGA2 算法的多目标无功优化

3.1　算法原理

Deb提出的引入精英策略的快速非支配排序遗传算法[13](NSGA2)是一种比较新颖的多目标遗传优化算法。常规NSGA2 算法采用SBX(simulated binary crossover)算子来模拟二进制交叉算子的过程，产生个体的方式如式(16)所示，α为随机变量，因为其搜索范围有限，容易出现局部最优以及进化过程中不稳定等问题[14]。针对SBX 算子的缺点，本文在交叉算子引入正态分布，如式(17)所示，用1.481|N(0,1)|代替随机变量α来扩大搜索空间；进一步将离散重组操作引入到式(17)中，得到了正态分布交叉(NDX)算子，如式(18)所示:

c1/2,i=[(y1,i+y2,i)±α×(y1,i-y2,i)]/2

(16)

c1/2,i=[(y1,i+y2,i)±1.481×|N(0,1)|×(y1,i-y2,i)]/2

(17)

(18)

式中：y1,i,y2,i为两个父代个体相对应的第i个变量；c1/2,i为其子代个体对应的第i个变量；N(0,1)为正态分布的随机变量；u为区间(0,1)上服从均匀分布的一个随机数。

3.2　配电网多目标无功优化算法实现流程

本文将NDX-NSGA2 算法应用到计及分布式电源和负荷功率不确定性的配电网多目标无功优化中，其流程如图1所示。

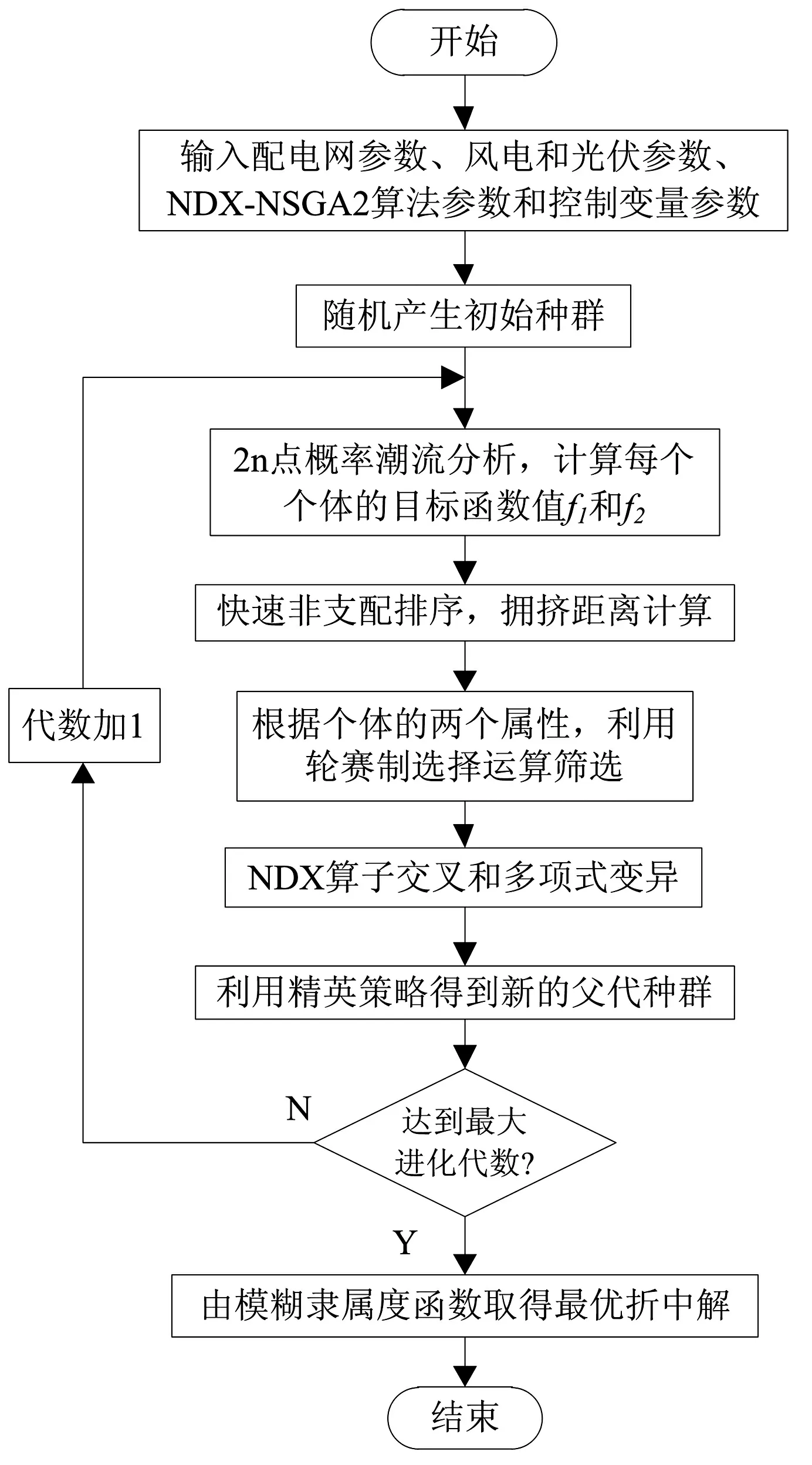
图1　基于NDX-NSGA2的配网多目标无功优化流程

4　算例分析

本文对标准IEEE33节点配网系统进行仿真，该系统线路参数及节点注入功率可参见参考文献[15]，该配电系统的基准电压为12.66 kV，基准功率为10 MVA，总有功和无功负荷功率给定值分别为3 715 kW 和2 300 kvar。以节点负荷功率给定值作为期望值，将负荷功率给定值的10%作为方差构造一组服从正态分布的随机数，作为节点的负荷概率模型。将在光伏发电系统和风电场分别安装在11号节点和24号节点，光伏发电系统由20个光伏电池阵列组成，光伏电池阵列由100个组件组成，单个组件的面积为2.16 m2，光电转换效率为13.44%，最大日照强度为0.5 W/ m2，形状参数α=0.28，β=2.05；风电场的风机型号采用VESTAS RRB 225，风电场输出的有功功率均值为225 kW，风机切入风速vci=3.5 m/s，额定风速vr=13.5 m/s、切出风速vco=25 m/s，采用的风速两参数威布尔模型，其尺度参数C=7.451 9，形状参数K=3.422 5[16]。在该配电系统的1、5、13和30号节点分别配置可投切的无功补偿电容器组，1和13号节点配置10组可投切电容器，每组电容器的容量为50 kvar，5和30节点配置20组可投切电容器，每组电容器容量为50 kvar。配置分布式电源和无功补偿电容器组后的IEEE33节点配网系统如图2所示。

图2　修改后的IEEE33配网系统

在本算例分析中，将NDX-NSGA2算法与常规NSGA2算法的种群规模和迭代次数分别设置为30和100。并利用模糊隶属度函数求取两算法Pareto解集中的最优折中解，如表1所示。

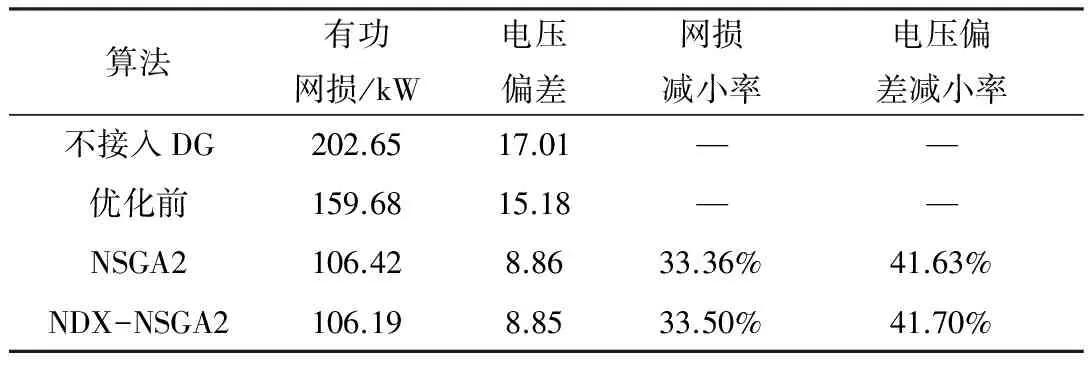
表1　IEEE 33节点配电系统优化结果

为了验证两点概率潮流法在考虑分布式电源和负荷不确定性配电网多目标无功优化中的有效性，根据给定和负荷模型和分布式电源模型，利用蒙特卡罗法产生10 000组随机数，并利用NDX-NSGA2算法进行优化计算，得到的最优折中解如表2所示。从表中可以看出由两点法得到的结果与蒙特卡罗法非常接近，且两点法的运算时间要远远小于蒙特卡罗法的运算时间，这说明两点法能够有效解决配网中分布式电源和负荷的随机性和波动性，可以较精确处理考虑分布式电源和负荷不确定性的配电网无功优化问题。

表2　两点法与蒙特卡罗法的比较

5　结束语

本文计及配电网无功优化中分布式电源和负荷功率的不确定性，提出采用两点估计法处理配电网无功优化中的概率潮流问题。建立了以有功网损和节点电压偏差最小为目标的有源配电网多目标无功优化模型，采用NDX-NSGA2 算法进行模型求解。仿真结果表明相比于常规NSGA2算法，NDX-NSGA2算法可得到更好的最优折中解，减小了系统的有功损耗同时提高了节点电压水平，更好地满足了配电网多目标无功优化的需求。且两点估计法的计算结果与蒙特卡罗法非常接近，表明两点法能够有效解决配网中分布式电源和负荷的随机性和波动性，验证了本文所提的方法的正确性和有效性。

参考文献：

[ 1 ] 王守相, 王慧, 蔡声霞. 分布式发电优化配置研究综述[J]. 电力系统自动化, 2009, 33(18):110-115.

[ 2 ] 张丽, 徐玉琴, 王增平,等. 包含分布式电源的配电网无功优化[J]. 电工技术学报, 2011, 26(3):168-174.

[ 3 ] 吕忠, 周强, 蔡雨昌. 含分布式电源的DEIWO算法配电网无功优化[J]. 电力系统保护与控制, 2015,43(4):69-73.

[ 4 ] 陈海焱, 陈金富, 段献忠. 含风电机组的配网无功优化[J]. 中国电机工程学报, 2008, 28(7):40-45.

[ 5 ] 刘沛津, 谷立臣. 含风电场的电力系统无功规划优化[J]. 电网技术, 2010, 34(7):175-180.

[ 6 ] 汪文达, 崔雪, 马兴,等. 考虑多个风电机组接入配电网的多目标无功优化[J]. 电网技术, 2015, 39(7):1860-1865.

[ 7 ] RABIEE A, SOROUDI A, MOHAMMADI-IVATLOO B, et al. Corrective voltage control scheme considering demand response and stochastic wind power[J]. IEEE Transactions on Power Systems, 2014, 29(6):2965-2973.

[ 8 ] 朱星阳, 张建华, 刘文霞,等. 风电并网引起电网电压波动的评价方法及应用[J]. 电工技术学报, 2013, 28(5):88-98.

[ 9 ] JANGAMSHETTI S H, RAN V G. Optimum siting of wind turbine generators[J]. Energy Conversion IEEE Transactions on, 2001, 16(1):8-13.

[10] 王成山, 郑海峰, 谢莹华,等. 计及分布式发电的配电系统随机潮流计算[J]. 电力系统自动化, 2005, 29(24):39-44.

[11] 李雪, 李渝曾, 李海英. 几种概率潮流算法的比较与分析[J]. 电力系统及其自动化学报, 2009, 21(3): 12-17.

[12] MOHSENI-BONAB S M, RABIEE A, MOHAMMADI-IVATLOO B, et al. A two-point estimate method for uncertainty modeling in multi-objective optimal reactive power dispatch problem[J]. International Journal of Electrical Power & Energy Systems, 2016, 75.

[13] DEB K, PRATAP A, AGARWAL S, et al. A fast and elitist multiobjective genetic algorithm: NSGA-II[J]. IEEE Transactions on Evolutionary Computation, 2002, 6(2):182-197.

[14] 李智欢, 段献忠. 多目标进化算法求解无功优化问题的对比分析[J]. 中国电机工程学报, 2010,30(10):57-65.

[15] 王守相,王成山. 现代配电系统分析[M]. 北京：高等教育出版社, 2007.

[16] 杨咏昕, 葛耀君, 项海帆. 风速风向联合分布的平均风统计分析[J]. 结构工程师, 2002,18(3):29-46.