基于改进遗传算法的自动化制造单元调度
毛永年,唐秋华,张利平
(1.武汉科技大学冶金装备及其控制教育部重点实验室,湖北 武汉,430081; 2.武汉科技大学机械传动与制造工程湖北省重点实验室,湖北 武汉,430081)
自动化制造单元是一类以机器人为物料运输工具的自动化生产系统,应用十分广泛。工件在此类制造单元中的加工通常具有一定的弹性,也就是工件的加工时间可以在给定的上下限范围(即时间窗口)内变动。物料搬运机器人必须在给定的时间窗口内,将工件从当前工作站转移到下一工序所在的工作站。为了便于管理,自动化制造单元常采用循环生产模式,即物料搬运机器人在每一个生产循环内执行相同的搬运作业序列。规划与调度机器人的搬运作业对提高系统生产效率、保证产品质量具有重要意义。
针对自动化制造单元调度问题,以数学规划和分支定界为主的精确求解算法有一定的优势,但是,随着问题的拓展和深入,此类方法易受到问题规模和输入参数(例如时间窗口)的限制。部分研究者考虑用启发式或元启发式算法求解最基本的自动化制造单元调度问题。Lim[1]提出了基于机器人搬运顺序编码的遗传算法。李鹏等[2]采用工件加工时间编码方式,将混沌思想引入遗传算法求解此类问题。晏鹏宇等[3]使用启发式方法构造遗传算法的初始种群,以增加其中的可行解数量。考虑到时间窗口约束导致问题可行解空间非常狭窄,王跃岗等[4]在使用量子进化算法求解时,进一步利用Levner等[5]提出的多项式算法来构造初始种群,同时针对进化过程中产生的不可行解引入了基于图论的修复策略。Lei等[6]基于工件在工作站的初始分配,采用0-1编码并使用启发式方法构造工件初始分配所对应的机器人搬运作业序列,同时提出了启发式修复策略修复不可行解。该研究由于在量子进化算法中融入了大量的启发式策略,虽然算法的搜索效率明显提高,但是针对特定类型案例的求解精度还有待于改善。
为了克服基本遗传算法容易陷入局部最优这一缺陷,本文设计一种改进遗传算法,采用基于循环序列的编码排列方式并配合两点交叉操作,以保证算法进化过程中种群的多样性。针对所研究问题可行解空间非常狭窄这一特点,本文提出启发式目标函数,以便在可行解很少甚至无可行解时,依然能够指引种群朝着有利方向进化。对于不可行解采用联动修复机制,自适应调整待修复的目标基因片段。同时引入禁忌表记录各基因的移动方向以避免对基因的盲目移动,从而保证算法的搜索效率和求解质量。最后,使用现有文献中的基准案例来验证本文算法的有效性。
1 问题描述和数学模型
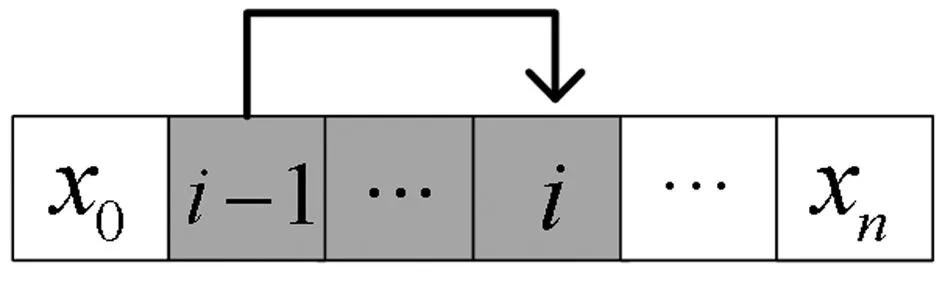
图1所示为本文研究的自动化制造单元,包括一个物料搬运机器人、n个工作站、装载站(编号为0)和卸载站(编号为n+1)。每个工件自装载站进入系统,依次从工作站1到工作站n后,被机器人卸载到站点n+1。装载站和卸载站的容量设为无限大。每个工作站在任何时候最多只能加工一个工件。由于工作站之间没有缓冲区,工件在当前工作站完成加工后(要满足时间窗口约束),必须立即被机器人运输到下一个工序所在的工作站。
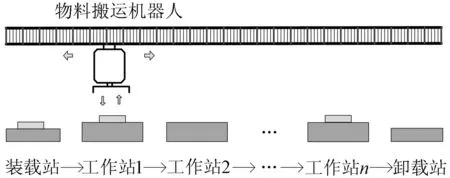
图1 自动化制造单元示例
为了方便模型的表述,定义如下参数:①搬运作业i,即机器人将工件从工作站i上取出,然后将其搬运到工作站i+1并将其卸载的全部过程,0≤i≤n;②ai、bi分别为工件在工作站i上的加工时间下限和上限,1≤i≤n;③di为执行搬运作业i所需的时间,0≤i≤n;④ci,j为机器人空载时从工作站i到工作站j的移动时间,0≤i,j≤n+1;⑤M为一足够大的正数。
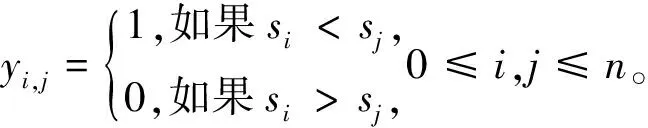
该问题的混合整数规划模型可以表示为:
minT
s.t.:
si-si-1+di-1≥ai-M(1-yi-1,i),1≤i≤n
(1)
si-(si-1+di-1)≤bi+M(1-yi-1,i),1≤i≤n
(2)
(si+T)-(si-1+di-1)≥ai-Myi-1,i,1≤i≤n
(3)
(si+T)-(si-1+di-1)≤bi+Myi-1,i,1≤i≤n
(4)
sj-si≥di+ci+1,j-M(1-yi,j),0≤i,j≤n
(5)
si-sj≥dj+cj+1,i-Myi,j,0≤i,j≤n
(6)
s0=0
(7)
si≥0,1≤i≤n
(8)
T≥si+di+ci+1,0,0≤i≤n
(9)
模型的目标函数是最小化周期长度T。式(1)~式(4)为时间窗口约束。yi-1,i=1时,即工件加工的开始和结束时间都在同一个周期内,则工件的加工时长为si-(si-1+di-1),而式(1)~式(2)表示这时工件的加工时长不小于其允许的下限值ai同时不大于上限值bi。yi-1,i=0时,即工件加工的开始时间要晚于其结束时间,这意味着工件在工作站i上的加工跨越了两个周期,那么工件的实际加工时长为(si+T)-(si-1+di-1),式(3)~式(4)表示这时工件的加工时长同样不小于其下限值ai同时不大于上限值bi。式(5)~式(6)为机器人移动能力约束,即机器人完成一项搬运任务后,必须有足够的时间移动到下一个搬运作业的开始位置。不失一般性,式(7)表示机器人在装载站上开始装载工件的时刻为一个周期的开始时刻。式(8)限制所有搬运作业的开始时间为正。式(9)强调周期T的长度必须不小于任何搬运作业完成后机器人回到装载站的时间。
2 改进遗传算法的设计
2.1 编码方式和种群初始化
本文采用整数编码,直接将搬运作业的序号作为染色体的基因组成。设X={x0,x1,…,xn}为种群中的一条染色体,其中xi为一个周期内的第i次搬运作业的编号。下面以6项搬运任务为例来说明此类编码方式。在传统编码方式中(见图2(a)),通常将搬运作业0作为序列的第一个搬运任务。考虑到所研究问题的循环特性,以任意搬运作业为首的序列都可以等价转换为以搬运作业0为起始位置的序列。例如,图2(b)中循环序列的编码排列事实上与图2(a)中的序列等价。为了克服算法容易陷入局部最优这一缺点,本文采用如图2(b)所示的以任意搬运作业为首的编码方式(循环序列),并采用完全随机初始化的方式保证搬运作业序列的多样化。
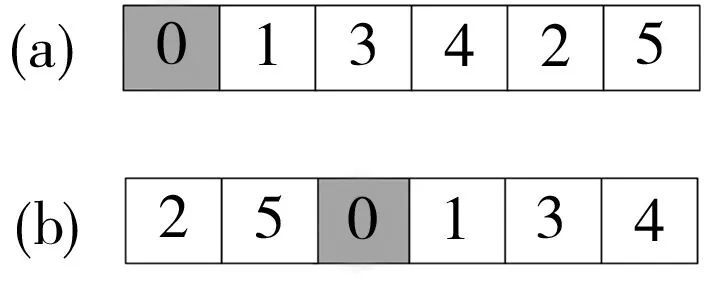
图2 两种等效的编码方式
2.2 交叉、变异操作
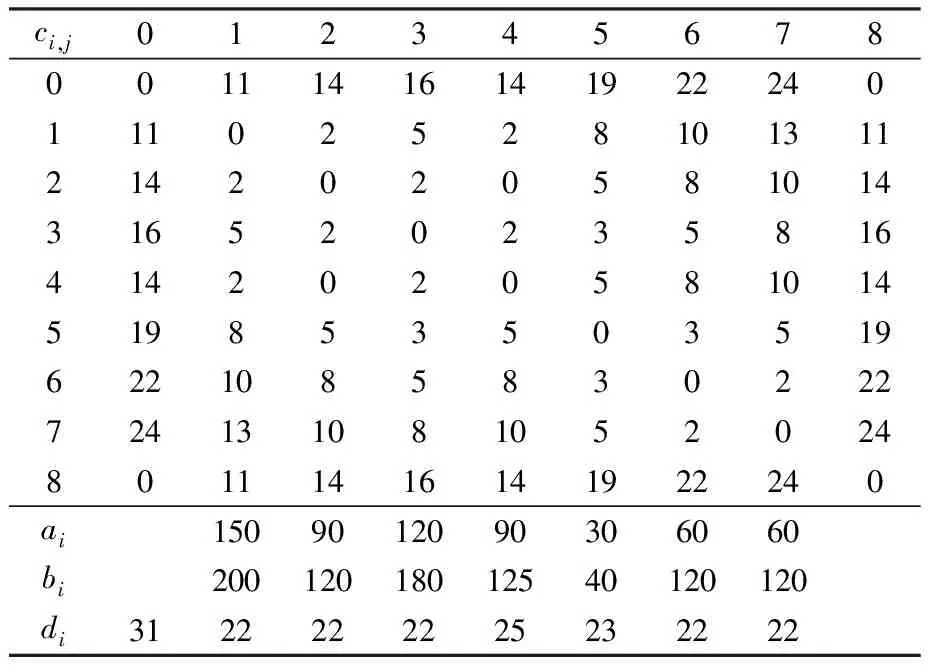
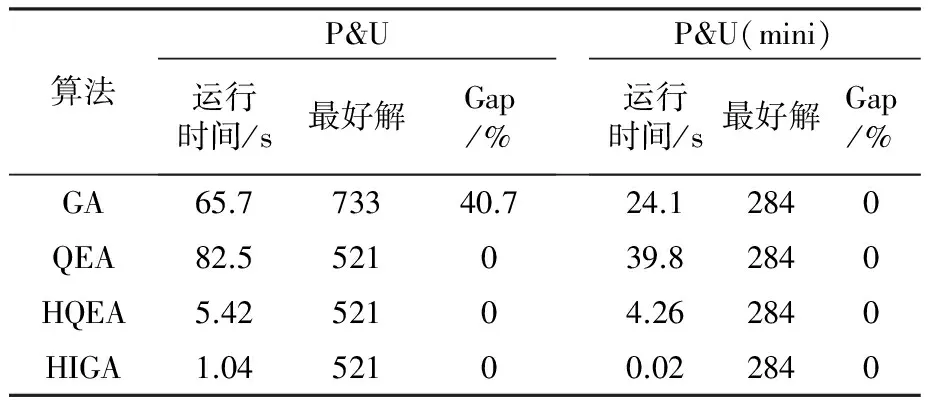
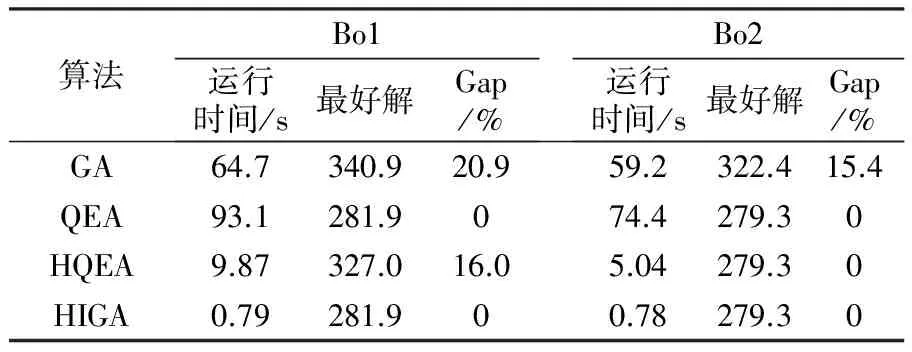
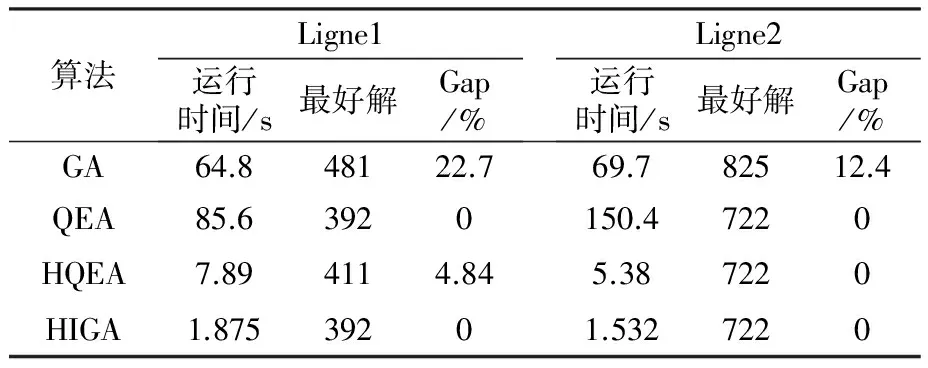
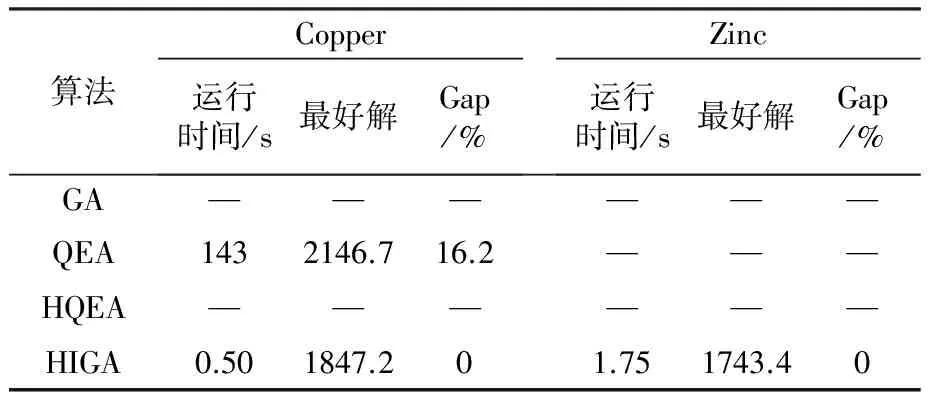
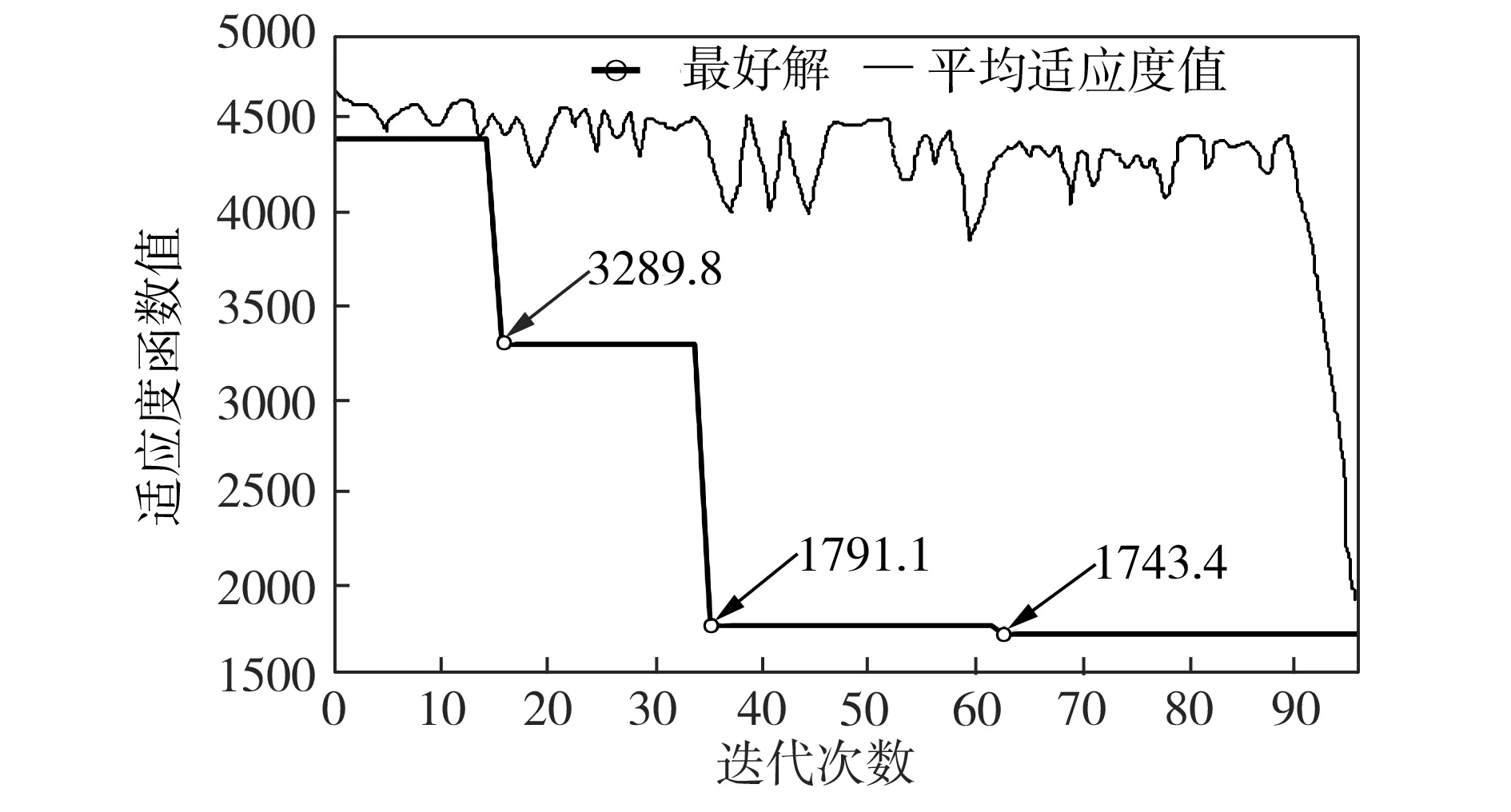
为了使优良的基因片段在进化过程中被保留下来,本文采用两点交叉操作,如图3所示。首先用锦标赛选择法从种群中挑出两条竞争获胜的染色体,记为父代1和父代2。随机从基因位置0~n中选取两点p1和p2(p1 图3 两点交叉操作 对于任意给定的一个可行染色体(机器人搬运作业序列),使用下式计算染色体适应度值: f1=T (10) 根据染色体基因编码可得到决策变量yi,j,则式(1)~式(9)可转换为如下形式: sj-si≥α+βT,0≤i,j≤n (11) 式中:α为实数;β的取值为-1、0或1。 事实上,式(11)是一类特殊的线性规划问题,可以用赋权有向图[7]来描述,Levner等[8]将其归纳为带参数的最短路径问题,并基于Bellman-Ford算法提出计算复杂度为O(n2m)的多项式>算法,此处n为图的节点数量,m为图中弧的数量。 染色体X的不可行主要由机器人移动能力不能满足工件的加工时间窗口所导致。当yi-1,i=1时,若如图4所示的部分序列i-1→…→i不可行,则整个染色体X一定不可行;当yi-1,i=0>时,若如图5所示的部分序列i-1→…→i不可行,则整个染色体X同样不可行。 图4 搬运作业i在i-1之后 图5 搬运作业i在i-1之前 为了方便描述,定义序列Si为染色体X中分别以搬运作业i-1开始、搬运作业i结束的一串有序子序列i-1→…→i。由于一个完整的染色体X包含n个如图4或图5这样的子序列,因此,任意一个子序列不可行都会导致整个染色体不可行。值得强调的是,交叉、变异操作会产生大量的不可行解,这些不可行解代表了种群的进化信息,为了区分这些不可行解,记参数ω为所有不可行子序列S的个数之和,并采用式(12)来计算不可行染色体的适应度值: f2=ω3 (12) 为了统一染色体适应度值的计算,本文采用式(13)来计算任意一个染色体的适应度值。 F=T+ω3 (13) 对于子序列Si={i-1,…,i},可采用下面的算法来判断其可行性。 输入:子序列Si。 输出:0 或 1。∥0表示子序列Si可行,1表示子序列Si不可行。 步骤1计算子序列Si的长度,记为R,设置t[0]←0。 步骤2 Forj=1 toR-1do t[j]←t[j-1]+dSi[j-1]+cSi[j-1]+1,Si[j]; Fork=0 toj-1do IfSi[k]+1=Si[j],then t[j]←max(t[j],t[k]+dSi[k]+aSi[k]+1) End End End 步骤3Ift[R-1]≤t[0]+dSi[0]+bSi[0]+1, thenreturn0; elsereturn1。 针对不可行解的修复策略对提高算法的运行效率十分关键。由于机器人移动能力约束和时间窗口约束具有很强的耦合性,仅仅修复某个特定的子序列往往会导致其它的子序列不可行,从而严重影响修复策略的实际效果。本文提出在修复不可行子片段Si时采用联动机制,即在修复Si子片段后同时修复与其相关的上游子片段Si-1或者下游子片段Si+1,并根据搜索进程不断更新修复目标S,直到满足终止条件。同时,使用方向禁忌表v记录染色体X中各基因的移动方向,从而避免迂回搜索。不可行解修复策略的具体操作步骤如下。 输入:染色体X,修复次数η。 输出:染色体X′。 步骤1设置向量v[]←0;参数obj←1,g1←0,g2←0,p1←0,p2←0,n←0。 步骤2Ifn>η,then进入步骤7; elsen←n+1,进入步骤3。 步骤3∥找到需要修复的子片段Si。 探测染色体X的每一个子序列S,找到最大不可行子片段Si。分别设置g1、g2为片段Si的第一个元素以及最后一个元素,同时设置p1为g1在染色体X中的位置,设置p2为g2在染色体X中的位置。 步骤4∥确定需要移动的目标基因obj,若obj=1,表示移动基因g1,否则移动基因g2。 Ifv[g1]!=-1 &&v[g2]=1,then obj←1,v[g1]←1; elseifv[g1]=-1 &&v[g2]!=1,thenobj←0,v[g2]←-1; elseifv[g1]=-1 &&v[g2]=1,then 进入步骤7; else IfRand()<0.5,thenobj←1,v[g1]←1; elseobj←0,v[g2]←-1; End End 步骤5∥移动目标基因。 Ifobj=1,then在染色体X中顺时针移动基因g1直到子序列S={g1,…,g2}可行; else在X中逆时针移动g2直到子序列S={g1,…,g2}可行。 分别用p1、p2记录g1、g2在染色体X中的位置。 步骤6∥探测上游或下游序列是否可行。 Ifobj=1,then探测序列Sg1(以g1-1为首的子序列)是否可行,如果该序列可行,则进入步骤2,否则,设置g1←g1-1,g2←g1+1,obj←1,v[g1]←1,进入步骤5。 else探测序列S(g2+1)(以g2为首的子序列)是否可行。如果该序列可行,则进入步骤2,否>则,设置g1←g2,g2←g1+1,obj←0,v[g2]←-1,进入步骤5。 End 步骤7输出染色体X′,停止。 上节所述的不可行解修复策略对算法进化过程中产生的不可行染色体进行了高强度的邻域搜索。为了提高算法的运行效率和收敛速度,局部搜索策略只针对可行染色体。具体搜索过程为:以交叉、变异操作后种群中出现的可行染色体为参照对象,对每个基因采用右邻基因交换的方式产生新解,选取产生的n+1个新解中最好的一个个体与参照对象进行对比,只要该新解的适应度值不大于参照对象的适应度值,则用该新解替换参照对象。 综上,本文设计的改进遗传算法步骤如下: 步骤1设置种群规模N、交叉概率Pc、变异概率Pm、最大修复循环次数η以及最大迭代次数π1和π2,并初始化迭代计数器n←0、μ←0。 步骤2随机初始化种群。 步骤3评价当前种群,如果有优于全局最优解的新解产生,则保存该新解并设置μ←0,否则,运用精英保留策略,即用全局最优解替换当前种群中的最差解,同时设置μ←μ+1。 步骤4设置n←n+1。如果n>π1或者μ>π2,算法停止。 步骤5进行交叉、变异操作。 步骤6对当前种群中的可行解进行局部邻域搜索,对种群中的不可行解进行可行性修复。跳转到步骤3。 为了检验算法的有效性,在CPU主频为2.30GHz的PC机上使用C++语言对所提出的改进遗传算法进行编码。相关参数设置为:种群规模N=20,交叉概率Pc=0.9,变异概率Pm=0.1,不可行解的最大修复循环次数η=5,最大迭代次数π1=1000以及π2=100。 采用本文提出的基于启发式目标函数和不可行解修复策略的改进遗传算法(HIGA)求解现有文献中的基准案例,包括P&U、P&U(mini)、Lignel、 Ligne2、 Bo1、Bo2、Copper 和Zinc。这些案例的原始数据来源于文献[9-11],其中案例P&U(mini)是案例P&U问题规模缩小后的版本,使用的原始数据在表1中列出。值得强调的是,本文首次使用元启发式算法求解了基准案例Copper和Zinc并报道了求解结果。全部案例的测试结果分别在表2~表5中列出,作为对照,表中同时给出了遗传算法(GA)[1]、量子进化算法(QEA)[4]以及基于启发式的量子进化算法(HQEA)[6]的测试结果。表2~表5中,“Gap”表示算法所获得的最好解与最优解之间的百分偏差,“—”表示该算法无法获得可行解。 表1 本文使用的基准案例P&U(mini)的测试数据 表2基准案例P&U和P&U(mini)的测试结果 Table2TestresultsofbenchmarkproblemsP&UandP&U(mini) 算法P&U运行时间/s最好解Gap/% P&U(mini)运行时间/s最好解Gap/%GA65.773340.724.12840QEA82.5521039.82840HQEA5.4252104.262840HIGA1.0452100.022840 表3基准案例Bo1和Bo2的测试结果 Table3TestresultsofbenchmarkproblemsBo1andBo2 算法Bo1运行时间/s最好解Gap/% Bo2运行时间/s最好解Gap/%GA64.7340.920.959.2322.415.4QEA93.1281.9074.4279.30HQEA9.87327.016.05.04279.30HIGA0.79281.900.78279.30 表4基准案例Ligne1和Ligne2的测试结果 Table4TestresultsofbenchmarkproblemsLigne1andLigne2 算法Ligne1运行时间/s最好解Gap/% Ligne2运行时间/s最好解Gap/%GA64.848122.769.782512.4QEA85.63920150.47220HQEA7.894114.845.387220HIGA1.87539201.5327220 表5基准案例Copper和Zinc的测试结果 Table5TestresultsofbenchmarkproblemsCopperandZinc 算法Copper运行时间/s最好解Gap/% Zinc运行时间/s最好解Gap/%GA——————QEA1432146.716.2———HQEA——————HIGA0.501847.201.751743.40 从测试结果来看,使用文献[1]中的GA求解这些基准案例的效果非常不理想,而使用了启发式初始化和修复策略的QEA获得了常规基准案例P&U、P&U(mini)、Lignel、Ligne2、Bo1和Bo2的最优解。HQEA考虑到问题特征,采用启发式方法进行解码,从而缩减了算法搜索的解空间,因此其求解效率要明显高于QEA,但是启发式的解码方法难免丢失最优解,从而导致HQEA在求解某些案例时存在局限性。对于案例Bo1和Ligne1,HQEA给出的结果和最优解有一定的偏差;对于案例Copper和Zinc,HQEA则不能给出任何可行或者较满意的解。 本文提出的基于启发式目标函数和不可行解修复策略的改进遗传算法(HIGA),以最短的运行时间给出了全部基准案例的最优解,其原因在于:一方面,算法进化过程中产生的大量不可行解代表了种群的进化信息,如果全部平等对待则会丢失部分有用的信息,从而导致算法进入盲目的无序搜索状态,尤其是当可行解数量非常有限时(例如案例Copper和Zinc),如果不用启发式目标函数对不可行解进行筛选,则很难在迭代过程中将有用信息进行积聚从而为发现可行解提供可能;另一方面,本文采用的不可行解修复策略不是简单修复某一串基因,而是使用联动修复机制对不可行染色体进行反复深度修复,从而使染色体最大可能地朝着目标函数优化的方向进行调整。 图6为HIGA求解案例Zinc的收敛曲线。由图6可见,最好解的迭代曲线跳跃很大。在第15代以前,算法没有找到任何可行解。在第15代时找到可行解3289.8,之后算法连续约20代没有进化,随后又突然找到可行解1791.1,最后停滞30代后找到了最优解1743.4。虽然种群的平均适应度值一直上下波动,但是总体趋势是变小的。这说明,虽然大多数时候最好解没有得到更新,但是种群始终是向好的方向进化的,因此算法获得更好解的概率随迭代的累积而不断增大。 图6 HIGA求解案例Zinc的收敛曲线 Fig.6ConvergencecurveofbenchmarkproblemZincbyHIGA 针对带时间窗口的自动化制造单元调度问题,本文提出了一种改进遗传算法。以启发式目标函数引导种群进化方向,采用循环序列的编码排列方式并配合两点交叉操作,尽可能地保证了进化过程中种群的多样性。在评价种群时,为了提高算法运行效率,首先对染色体的可行性进行判别从而减少了采用精确算法评价种群个体的计算复杂度。针对不可行解,采用联动修复机制,根据修复过程自适应调整待修复目标片段,同时引入禁忌搜索的思想避免了算法的盲目搜索,提高了算法的搜索效率和求解质量。对现有文献中基准案例的测试结果验证了本文算法求解此类问题的有效性。 [1]Lim J M. A genetic algorithm for a single hoist scheduling in the printed-circuit-board electroplating line[J].Computers and Industrial Engineering,1997,33(3/4):789-792. [2]李鹏,车阿大.基于混沌遗传算法的自动化生产单元调度方法[J].系统工程,2008,26(11):75-80. [3]晏鹏宇,车阿大,李鹏,等. 具有柔性加工时间的机器人制造单元调度问题改进遗传算法[J].计算机集成制造系统,2010,16(2):404-410. [4]王跃岗,车阿大.基于混合量子进化算法的自动化制造单元调度[J].计算机集成制造系统,2013,19(9):2193-2201. [5]Levner E, Kats V, Levit V E. An improved algorithm for cyclic flowshop scheduling in a robotic cell[J].European Journal of Operational Research,1997,97(3):500-508. [6]Lei W D, Manier H, Manier M A, et al. A hybrid quantum evolutionary algorithm with improved decoding scheme for a robotic flowshop scheduling problem[J].Mathematical Problems in Engineering, 2017,2017:3064724. [7]KatsV,LevnerE.Cyclicroutingalgorithmsingraphs: performance analysis and applications to robot scheduling[J].Computers and Industrial Engineering,2011,61(2):279-288. [8]Levner E, Kats V. A parametric critical path problem and an application for cyclic scheduling[J].Discrete Applied Mathematics,1998,87(1-3):149-158. [9]Phillips L W, Unger P S. Mathematical programming solution of a hoist scheduling program[J].AIIE Transactions,1976,8(2):219-225. [10] Chtourou S, Manier M A, Loukil T. A hybrid algorithm for the cyclic hoist scheduling problem with two transportation resources[J]. Computers and Industrial Engineering,2013, 65(3):426-437. [11] Leung J M Y, Zhang G Q, Yang X G, et al. Optimal cyclic multi-hoist scheduling: a mixed integer programming approach[J]. Operations Research, 2004,52(6):965-976.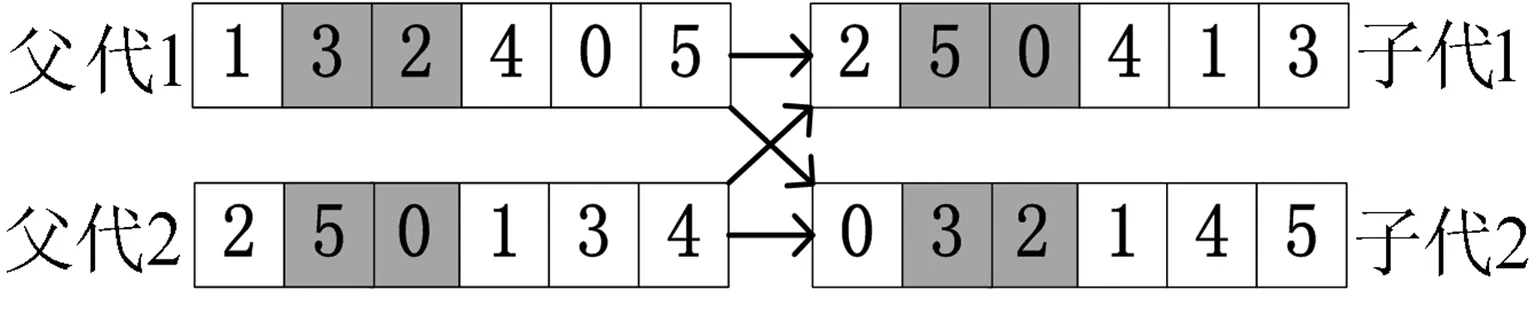
2.3 启发式评价函数
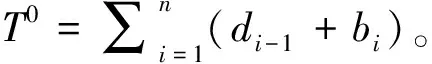

2.4 不可行解修复策略
2.5 局部邻域搜索
2.6 改进遗传算法步骤
3 算法验证
4 结语
——《行政科学论坛》杂志工作站挂牌运行

